岩体完整性对载荷干扰定量分析的影响<br/>——以天津小辛庄应变为例

岩体完整性对载荷干扰定量分析的影响
——以天津小辛庄应变为例

2021-02-14雷生学刘建波

地震地质 2021年6期

关键词：节理完整性岩石

雷生学刘建波闫伟宋田

李昊5）李恩健1）朱冰清1）李颖楠1）

1）天津市地震局，天津 300201

2）防灾科技学院，三河 065201

3）中国地震局地质研究所，北京 100029

4）中国地震台网中心，北京 100045

5）西安雅通智能科技公司，西安 710048

0 引言

定点形变观测（如地倾斜或应变观测）是监测地壳形变和捕捉地震前兆的重要手段（牛安福等，2013）。因具有高精度、宽频带及连续性好等优点，定点形变观测与InSAR及GPS同为地壳运动和形变观测的主要手段（邱泽华，2004；Fréchetetal．，2012）。在过去的几十年间，中外学者针对形变观测的应用研究，特别是在尝试性捕捉地震前兆信息方面进行了有益的探索，取得了较为丰硕的成果（张晶等，2009；邱泽华等，2010；牛安福等，2012，2013；邱泽华，2014；闫伟等，2015；杨小林等，2018，2020；黄浩等，2019；贾媛等，2019），例如：1976年意大利东北的福留利（Friuli）6.5级地震前，距震中NW 约15km的水平摆观测到约200″的S倾变化，被认为是成功捕捉到的地震前兆异常（Dragonietal．，1984）；Timofeev等（2015）研究发现，俄罗斯贝加尔湖Talaya台的水平摆对台站周边200km范围内发生的中等地震有较好的响应；龙门山断裂带西南端姑咱台的钻孔应变记录于汶川地震和芦山地震前均观测到一系列“毛刺”突跳变化，研究者分析认为这是比较可靠的地震前兆异常（池顺良等，2009，2013；邱泽华等，2010；Qiuetal．，2013）。这些成功的案例表明，定点地壳形变观测在地震前兆研究乃至地震预测方面具有广阔的应用前景。

然而，众所周知，在定点形变的日常观测中，会经常碰到各种“载荷干扰”，如强降雨、水库、河流、开挖山体、建筑施工等，而准确定量评估此类干扰对地震前兆异常识别、判断地震形势及地震预测研究等有着重要意义。近年来，数值模拟技术在定量评估载荷干扰的影响方面取得了长足的进展（邱泽华，2004；闫伟等，2015；杨小林等，2018，2020；朱冰清等，2019）。但是，存在的一个突出的问题是：在进行数值模拟分析时，不少研究（特别是形变学科的异常核实报告）没有考虑具体场地岩体的完整度（岩体是较为完整还是比较破碎），而是简单地采用了通用的“岩石弹性模量”，使得外界载荷干扰的影响被“低估”，从而影响干扰的排除或前兆异常的识别，甚至为地震形势预测提供误导性信息。例如，马栋等（2014）采用三维有限线段载荷模型计算分析了河流清淤和蓄水对河北张家口体应变的影响，得到的理论值仅占实际观测值的1%～2%，从而认为此次异常存在着其他影响因素；朱冰清等（2019）利用不规则载荷模型分析了于桥水库对天津蓟县水管倾斜观测的影响，认为于桥水库并不是一个显著干扰源，其贡献仅为2%～3%；2019年6月辽宁抚顺台洞体应变出现异常，研究人员分析后认为，台站附近河流水位的上涨不是洞体应变大幅快速拉张的主要因素，从而将此次异常认定为地震“前兆异常”(1)辽宁省地震局，2019，2019年6月辽宁抚顺台洞体应变观测异常核实报告。。但是，经仔细分析后可以发现，上述研究中皆没有考虑研究区内岩体的完整性对弹性模量的影响，而弹性模量的取值大小对计算载荷干扰的贡献有着举足轻重的作用。

本文中，我们以天津蓟县小辛庄的洞体应变为例，来说明在定量分析时必须考虑岩体的完整或破碎程度，即应当采用“岩体”的弹性模量而非“岩石”的弹性模量，才能更准确地评估外界载荷干扰对形变观测的影响。首先，我们对小辛庄和于桥水库周围的岩体进行了详细的“节理统计”，随后利用岩体体积节理与弹性模量之间的关系确定了研究区内“岩体的弹性模量”，最后利用不规则载荷模型（闫伟等，2015）模拟计算了于桥水库蓄水对小辛庄应变的影响，从而揭示出2019年9—11月小辛庄应变出现的破年变异常并非是前兆异常，而极有可能是受于桥水库库容变化的影响所致。

1 岩体完整性的计算方法

1.1 岩体弹性模量与岩石弹性模量的关系

岩石弹性模量是一个重要的岩石力学参数，其含义为岩石在弹性范围内的应力与应变之比，与岩石类型、含水量、颗粒大小、孔隙大小等密切相关。在自然界，由于层理、节理、裂隙、断层等微构造的发育，使得岩体的完整性降低，因此，大范围天然岩体与小尺度岩石的弹性模量值有很大差别，这点在工程地质界已早有共识（杜时贵等，2000；胡修文等，2010；郭强等，2011；中华人民共和国国家标准编写组，2014）。

郭强等（2011）推导出岩体的弹性模量Em与岩石的弹性模量Er之间存在如下定量关系：

式中，Kv为岩体的完整性指数。可以看出，岩体与岩石的弹性模量成正比，其比例系数即为岩体的完整性指数。通常情况下，实际遇到的岩体多介于“较完整至破碎”级别（极完整或极破碎的情形十分罕见），对应的Kv值则介于0.75～0.15之间，这意味着常见岩体的弹性模量值显著减小，仅为完整岩石弹性模量的0.75～0.15倍。

1.2 岩体完整性指数K v的计算

岩体的完整（破碎）程度对岩体力学参数（弹性模量、泊松比等）有着重要影响（杜时贵等，2000；胡修文等，2010）。具体而言，研究发现岩体的弹性模量与其完整性之间存在着极为密切的关系：在相同的应力条件下，完整致密的岩体应变较小，其弹性模量值较大；反之，破碎松散的岩体应变较大，弹性模量值则较小（郭强等，2011）。

目前，描述岩体完整性的指标主要有3种，即岩体质量指标RQD（Rock Quality Designa tion）、岩体体积节理数Jv和岩体完整性指数Kv，其分别从钻孔取芯率、单位体积节理数和弹性纵波波速的角度描述岩体的完整程度（郭强等，2011），3种指标之间可以相互转换。

岩体完整性指数Kv是衡量岩体完整性的重要指标之一，为岩体与岩石的纵波波速之比的平方，可通过直接法得到，即利用专门的声波测量仪分别测定纵波在岩体和岩石中的传播速度获得。此外，岩体完整性指数还可通过间接的方法获得。前人研究认为，若岩体中的节理、裂隙等微构造越发育，即体积节理数Jv越高，则岩体的完整性越差（破碎度越高），相应的岩体完整性指数Kv也越小（林锋等，2008；胡修文等，2010），二者之间存在着定量转换关系。国标《工程岩体分级标准》（GB／T 50218－2014）（中华人民共和国国家标准编写组，2014）中以表格的形式给出了岩体体积节理数与岩体完整性指数的转换关系（表1），胡修文等（2010）据此拟合出二者之间的计算公式：当3＜Jv＜35时，二者为线性关系（式（2））；而当Jv＞35时，二者为负指数关系（式（3））。因此，可通过野外测量岩体体积节理数的方式得到岩体的完整性指数。

表1 岩体体积节理数J v与岩体完整性指数K v的对照表（据中华人民共和国国家标准编写组，2014）Table 1 Cross reference of volumetric joint count J v and rock mass integrity K v（from Code of Engineering Rock Mass Classification，GB／T 50218－2014）

综上，可以看出：若要得到岩体的弹性模量，首先需要在野外测量获得岩体的体积节理数，然后转换得到岩体的完整性指数，最后利用式（1）即可得到岩体的弹性模量。

1.3 岩体体积节理数J v的测量

节理指岩体受力后两侧岩块没有发生明显位移的断裂，是一种常见的地质构造（朱志澄，2008）。岩体体积节理数Jv指1m3岩体内节理的数目，是表征岩体完整性的重要指标之一（林锋等，2008）。目前，测量岩体体积节理数的方法主要有3种，即直接测量法、间距法和条数法（中华人民共和国国家标准编写组，2014）。直接测量法是在野外直接逐条数出单位体积岩体中的节理条数；间距法通过测量岩体中各组结构面的间距，取其平均值作为最终的结果；条数法，是统计出单位面积内的结构面条数，然后乘以修正经验系数。在野外选择有代表性的露头剖面或开挖壁面进行节理统计，每个测点的统计面积≥5×2m2。需要注意的是：1）被硅质、铁质、钙质等充填胶结的结构面，因其已不再成为分割岩体的界面，在确定Jv时，不予统计；2）对于延伸长度＞1m的随机性节理需统计在内，以使得Jv值更加符合实际情况（中华人民共和国国家标准编写组，2014）。

2 研究区的地质构造与仪器情况

天津蓟县小辛庄子台地处天津市北部的山区（图1），构造上位于燕山山脉与华北平原的交界处。燕山山脉在此出露的岩石主要为中元古界未变质的蓟县系雾迷山组和蓟县系杨庄组地层（白云岩、泥质白云岩、燧石白云岩、沥青质白云岩和叠层石等）（图2）；而山前平原区主要为第四系冲洪积物（类黄土、砂砾石等）。小辛庄台附近的主要断层为蓟县山前断裂（图1），该断裂近EW 向展布，长约60km，倾向S，为正断性质，构成燕山山脉与华北平原的分界。通常认为，蓟县山前断裂的活动时间为早、中更新世（Q1－2P ）(2)天津市地震局，2011，天津盘龙谷文化城项目工程场地地震安全性评价报告。。小辛庄台向S约2km为于桥水库（图1）。该水库于1959年建成，EW 向长约15km，SN向宽约6km，蓄水面积约为87km2，丰水期的库容量约为4亿立方米，枯水期则仅0.3～0.5亿立方米。小辛庄台使用SS－Y型伸缩仪进行应变观测，其分辨率优于1×10－9，年均漂移＜1×10－6。2019年9—11月，小辛庄应变NS分量出现“破年变下降异常”，累计下降幅度约为942×10－8（图3）。天津市地震局形变学科组分析认为，于桥水库对该异常的影响较小（仅为百分之几），不足以产生如此大的压缩量，故判断该异常是地震前兆异常的可能性较大(3)天津市地震局，2019，2019年9月天津蓟县小辛庄伸缩应变异常核实报告。。

图1 节理统计点（数字编号1～5）与小辛庄台（绿色三角）及于桥水库的相对位置Fig．1 Locations of joint statistics sites（in numbers 1～5），Xiaoxinzhuang seismic station（green triangle），and Yuqiao reservoir．

图2 小辛庄台周围的岩性地层（改自1 20万“兴隆幅”地质图）Fig．2 Lithology in Xiaoxinzhuang station and its vicinity（modified from the Geological Map（1 200 000）of Xinglong．

图3 小辛庄应变NS分量2018年以来的数据变化（虚线框为2019年9月认定的异常）Fig．3 N－S component of strain of Xiaoxinzhuang station since 2018（the curve in dashed rectangle is the anomaly recognized in September 2019）．

3 结果与分析

3.1 研究区岩体的体积节理数

对小辛庄台和于桥水库周围的岩性地层进行了详细的踏勘，发现有5处岩体的出露情况较好（见图1中的数字编号），可以满足节理统计的要求。依照国标《工程岩体分级标准（GB50218－2014）》（中华人民共和国国家标准编写组，2014）的规定，选取此5处剖面进行节理统计，采用条数法，每处剖面的统计点为4个或5个，取平均值作为体积节理数Jv的最终值。各剖面的岩性及节理发育的代表性照片见图4，具体的节理统计结果见表2。

经调查发现，研究区内主要发育2组区域性剪节理，平面上呈“X”形分布（如图4中的桃花寺东和李各庄剖面），一组剪节理的产状为96°∠81°，另一组则为351°∠84°，除此之外，还发育少量随机节理、局域性小节理及不规则裂隙等。另外，虽然普遍发育1套厚5～9m的厚层块状白云岩，但研究区内的地层主要以中厚—薄层产出（图4左列），层厚以5～30cm居多。这些规模不一的节理、层面及裂隙等结构面将研究区内的岩体分割为大小不一、支离破碎的岩块。

图4 各节理统计点的代表性照片Fig．4 Representative photos of all the joint statistic sites．各点的具体位置见图1；作为参照物的地质锤长约25cm

节理统计结果显示，小辛庄和于桥水库周围的岩体体积节理数均＞32条／m3（表2），表明研究区内的岩体比较破碎，尤其以李各庄和水库南的岩体最为破碎，其体积节理数分别达41条／m3和39条／m3。

3.2 研究区岩体的完整性指数

依据式（2）、（3）结合实测得到的研究区的岩体体积节理数计算出相应的岩体完整性指数Kv（表2），可以看出：研究区内的岩体完整性指数Kv值均＜0.19，最小值出现在李各庄，仅为0.10，而整个研究区的平均值则为0.14，表明小辛庄台和于桥水库周围岩体的完整性不高，较为破碎，这与野外观察得到的直观认识比较一致。

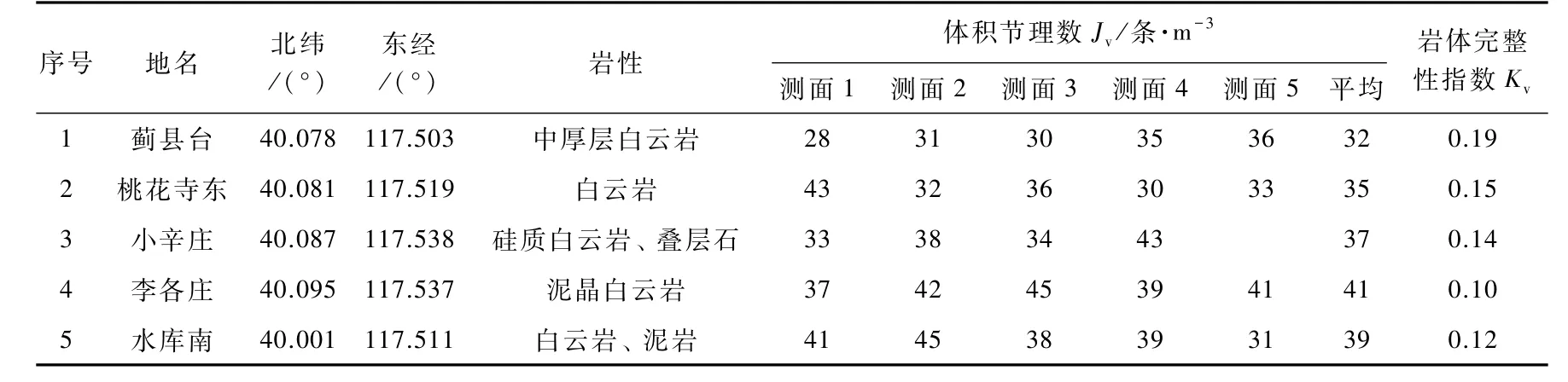
表2 小辛庄周围岩体的体积节理统计结果（各点的位置见图1）Table 2 Results of joint statistics in rocks around Xiaoxinzhuang（locations shown in Fig．1）

如前文所述，岩体的完整性指数即为岩体与岩石的弹性模量的比例系数。由此可知，小辛庄及于桥水库周围岩体的弹性模量仅为完整岩石的弹性模量的0.10～0.19倍，平均约为0.14倍，表明在相同的应力条件下，若考虑实际岩体的破碎程度，则外界载荷对小辛庄产生的应变将被放大1／Kv倍，即5～10倍（平均约7倍）。

3.3 于桥水库对小辛庄应变的影响分析

野外调查发现研究区内的岩石主要为白云岩、硅质或灰质白云岩及少量的叠层石和泥晶白云岩等（图2），白云岩的弹性模量为7～15GPa。上节的计算结果表明，研究区内岩体的弹性模量仅为完整岩石的0.10～0.19倍，平均约为0.14倍。因此，若以均值0.14作为参考，则研究区内岩体的弹性模量为（7～15）Ga×0.14＝（0.98～2.1）GPa。另外，白云岩的泊松比为0.15～0.35，在此选定为0.25。之所以选择较大的泊松比，是由于有研究表明岩体的泊松比除了受岩性影响外还与风化程度、节理裂隙发育等有关；若岩体较为破碎，其泊松比将相应较大（张国凯等，2016）。考虑到研究区的岩体比较破碎，故选择较大的0.25作为模拟参数。

利用闫伟等（2015）开发的“不规则载荷模型”程序计算于桥水库的库容变化对小辛庄伸缩NS分量的影响。选取2019年9月26日—11月25日和2020年4月1—22日2段蓄水期作为研究时段，这2次蓄水期内水库的水位分别上升了2.56m和0.84m（表3），在此期间，小辛庄伸缩NS分量皆表现为下降变化，相应的伸缩变化量分别为942.05×10－8和163.7×10－8，而相应的模拟计算结果则分别是（93.76～200.91）×10－8和（30.77～65.92）×10－8（图5），理论值占实际观测值的10%～21%和19%～40%，表明于桥水库的库容变化对小辛庄的应变观测有着重要影响。

图5 于桥水库蓄水（2019年9月26日—11月25日）对小辛庄NS向产生的位移场和应变场Fig．5 Disp lacement field and strain field around Xiaoxinzhuang produced by Yuqiao reservoir impoundment（2019－09－26—2019－11－25）．白色五角星为小辛庄台，不规则多边形为于桥水库

表3 于桥水库蓄水对小辛庄应变NS分量的影响Table 3 Influence of Yuqiao reservoir impoundment on the N－S component of strain of Xiaoxinzhuang station

4 讨论

4.1 岩体完整性对弹性模量及应变的影响

理论分析表明，在其他条件相同的情况下，弹性模量与应变呈负相关，即弹性模量越大，则相应的应变越小；若弹性模量越小，则相应的应变越大（邱泽华，2004）。另外，如前文1.2节所述，岩体的完整性与岩体的弹性模量呈正相关，若岩体的完整性越差（越破碎），其弹性模量将越小；反之，若岩体的完整性越好（越完整），则其弹性模量将越大。因此，综合以上结论可以得出：在相同的应力条件下，岩体的完整（破碎）度与应变呈负相关——岩体越完整，弹性模量越大，相应的应变将越小；反之，岩体越破碎，弹性模量越小，而相应的应变将越大。如此，岩体的完整（破碎）度Kv与“放大器”的影响类似，可使破碎岩体上的应变比完整岩石上的应变放大1／Kv倍（图6b）。

图6为依体积节理数来衡量的岩体完整度与岩体完整性指数（岩体弹性模量的比例系数）及相应的应变关系图，从中可以直观地看出：在相同的应力作用下，当岩体中的节理分别为20条／m3、30条／m3和40条／m3时，岩体的弹性模量分别仅为完整岩石弹性模量的0.35、0.22和0.12倍（图6a），而对应的应变则分别被放大了约2.9、4.6和8.7倍（图6b）——这清楚地表明在定量评估外界载荷的影响时，必须要考虑场地基岩的完整性。

图6 岩体完整度与岩体完整性指数（a）及其与应变（b）的关系Fig．6 Relationships between rock mass integrity and rock mass integrity index（a）and the corresponding strain（b）．

4.2 小辛庄应变及其他实例

2019年9—11月，天津小辛庄应变NS分量出现破年变下降异常，累计下降幅度约942×10－8。彼时，天津市地震局形变学科组分析认为，距离台站约2km的于桥水库蓄水所产生的载荷效应不足以产生如此大的压缩量，并初步估算其影响较小，仅为百分之几，故推断该异常是地震前兆异常的可能性较大。然而，此次调查研究发现：小辛庄及于桥水库周围的岩体比较破碎，其体积节理数＞32条／m3；研究区内岩体的弹性模量仅为完整岩石的0.10～0.19倍；不规则载荷模型的计算结果显示于桥水库蓄水对小辛庄伸缩NS分量产生的理论压缩应变约为（93.76～200.91）×10－8，约占实际观测值（942×10－8）的10%～21%。因此，推断2019年9—11月小辛庄应变的破年变异常并非是地震前兆异常，而更可能是受于桥水库库容变化的影响所致。

如上，理论计算结果显示于桥水库的贡献似乎略显小，仅为实际观测值的10%～21%，我们认为，这可能是由于数值模拟所采用的不规则载荷模型仅为一种高度简化的模型，其没有考虑岩性不均一、蓟县山前断裂、地下水的孔隙压力以及水库的蓄水面积变化等诸多影响因素。以前2项影响因素——岩性不均一和蓟县山前断裂为例，此次调查发现研究区内除了分布有较为破碎的白云岩外，还有少量泥岩、页岩及叠层石等，而这些岩石的弹性模量均比白云岩小；同样，蓟县山前断裂的存在也使得研究区的岩体更加破碎，即岩体的弹性模量更小。因此，若在定量分析时额外考虑这2种因素的影响，则于桥水库的贡献将会更大。

目前，在相当多的形变异常核实报告和一些其他类似研究中，研究者没有考虑研究区内岩体的完整（破碎）度对弹性模量的影响，而是简单地采用了通用的“岩石弹性模量”，而非“岩体弹性模量”，这样可能会使得外界载荷干扰的影响被显著“低估”。例如，2012年1—5月，河北张家口台附近进行河道清淤和蓄水作业，研究人员采用三维有限线段载荷模型分析了此次施工对体应变的影响，得到理论值仅占实际观测值的1%～2%，从而认为此次异常存在着其他影响因素（马栋等，2014）。然而，该台台址为较破碎—破碎的片麻岩（马栋等，2014），其弹性模量值应当比完整的片麻岩小很多，即施工影响的理论计算值应当更大。又如，与小辛庄在同一个研究区，且同样采用不规则载荷模型，研究者分析了于桥水库对蓟县水管倾斜观测的影响，认为水库库容的改变不足以对蓟县水管倾斜观测造成显著干扰（朱冰清等，2019）。然而，当考虑了岩体完整性的影响后再进行计算，则理论结果占实际观测值的10%～30%，这意味着于桥水库是一个显著的干扰源。