模拟退火算法与Python-ABAQUS结合的有限元模型修正方法研究

成 魁, 王祺顺,, 张祖军, 田仲初, 吴 欣

(1.广西交通科学研究院有限公司, 广西 南宁 530005; 2.湖南省交通科学研究院有限公司, 湖南 长沙 410015; 3.长沙理工大学, 湖南 长沙 410114)

0 引言

在对中低速磁浮轨道梁等复杂结构模型的仿真分析中，通常有限元模型单纯按设计图纸所给尺寸和材料参数等建立，往往得出的是理想的状态结果，考虑到结构实际的运行工作情况，此模型结果难以反映出轨道梁结构的实际工作状态，故需利用静动力试验分析结果，如挠度、应变、频率、振型、阻尼比等，在保证模型符合实际尺寸和精度的状态下，调整或修正部分由于施工质量、环境等因素影响的设计参数值，使计算结果与试验结果尽可能统一，从而更加逼近于实际状态。

1 工程概况

本文以长沙中低速磁浮交通工程(25+35+25)m连续梁桥为工程背景(见图1)，对其进行有限元模型修正研究。该桥单线轨道梁截面形式为单箱单室等高箱梁截面，单线轨道梁之间通过端横梁及中横梁连接，箱梁对应横梁位置设置隔板。梁高2.4m，箱梁顶板宽1.3m，底板宽1.4m，线间距4.4m，两线箱梁总宽5.7m。支座中心至梁端0.35m，箱梁横桥向每线下设一个支座，边、中支座横桥向中心距均为4.4m。

图1 (25+35+25)m双线连续轨道梁实拍现场图

2 初始有限元模型建立

为使所建立的模型更接近于磁浮轨道梁的现场实际运营的状态，本文利用ABAQUS软件对(25+35+25)m双线连续轨道梁主体结构和轨道结构均采用实体单元精细化模拟，桥墩与箱梁之间采用运动耦合形式，约束部分自由度来模拟实际的边界条件。

本文采用经验法与ABAQUS敏感度分析方法相结合来确定有限元模型修正的设计参数和设计响应。由于中低速磁浮轨道梁上部结构比较复杂，影响其动态特性的参数很多，如箱梁主体的质量与刚度、轨道结构的质量与刚度、桥墩的质量与刚度等，因此，在进行有限元模型之前确定适当的设计参数尤为重要。

各个参数影响不一，对于那些对轨道梁动力特性的影响较大的结构参数，才是有限元模型修正应该着重加以控制的设计参数，才能尽可能接近实际状态，确定实际桥梁的承载能力和工作性能，因此对众多的影响结构动力特性的参数进行敏感性分析就显得很有必要。

具体截面几何尺寸和材料参数主要依据工程施工图纸确定。

a.建模初始参数(见表1)。

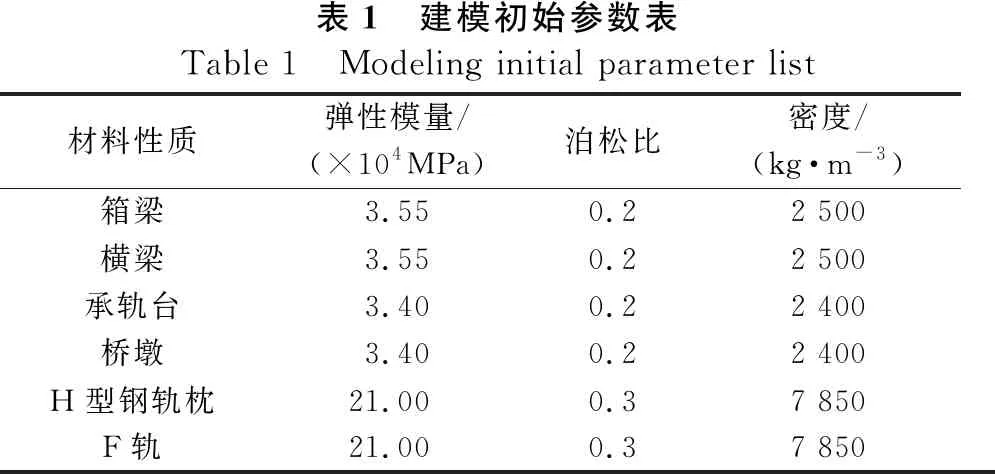
表1 建模初始参数表Table 1 Modeling initial parameter list材料性质弹性模量/(×104MPa)泊松比密度/(kg·m-3)箱梁3.550.22 500横梁3.550.22 500承轨台3.400.22 400桥墩3.400.22 400H型钢轨枕21.000.37 850F轨21.000.37 850

b.箱梁实际截面尺寸(见图2、图3)。

图2 轨道梁箱梁跨中断面的实际尺寸图(单位： cm)

图3 轨道梁箱梁支点断面的实际尺寸图(单位： cm)

c.轨道结构实际尺寸图(见图4)。

(a) 轨道梁轨道结构部分横断面图

d.建立的初始有限元模型(见图5)。

图5 ABAQUS初始有限元模型示意图

3 模拟退火优化算法

退火算法合理依据了物体退火结晶原理，当固体温度很高时，内部粒子处于快速且无序的运动状态，内部能量较大，当慢慢开始降低固体温度时，粒子的运动状态慢慢变得规则有序，其内部能量也开始慢慢减少，直到当固体的温度降至常温时，其内部能量可以达到最小，此时粒子的运动最为规则和稳定。该算法首先从指定的一个较高温度出发开始做迭代计算，随机生成一个初始解，并在该解的领域范围内做随机扰动产生一个新解，根据Metropolis，确认新解是否可接受，并且如不能满足程序终止条件，则以某种方式降温，并开始新的迭代。

exp(-ΔE/(kT))用于表示粒子在温度T下趋于平衡的概率，其中E为温度T时的内能，ΔE为其改变数；k为Boltzmann常数。Metropolis准则常表示为：

p=

将p与随机数α∈[0,1]进行比较，p<α，则接受xnew，用来替代xold，否则舍弃。该过程在不断循环重复中可产生新状态，直至系统能量最低的平衡状态，终止此过程。

将目标函数值f作为内能E模，控制参数t作为温度T，便可衍生出解组合优化问题的模拟退火演算法：从控制参数的初始值t与初始解i开始，重复当前解“① 产生新解；② 计算目标函数差；③ 接受或丢弃”，该循环在逐渐衰减t值的同时，最优解可进行近似处理。利用Cooling Schedule(冷却进度表)控制退火过程，恶化解可以在一定的概率下依据准则被接受。

模拟退火算法总共分为两层循环，其中一层循环是在初始解邻域范围内随机扰动产生一个新解并计算和比较两者目标函数值，决定是否被接受；而另一层则是由于算法给定的温度初始值较高，需经过一定数量的迭代才能缓慢降温，最终收敛得到全局最优解。具体步骤如下：

a.随机给出初始模型参数的初始解，并计算其目标函数值E(m0)。

b.设置温度初始值T0和迭代计数器t。

c.在初始解邻域范围内随机进行一个扰动，产生新的模型参数值m1=m0+Δm，并计算新的目标函数值E(m1)。

d.计算两种情况下的目标函数值之差ΔE，若ΔE≤0，接受新模型参数值，否则根据Metropolis标准以一定的概率可否接受新值。

e.若计算迭代次数t小于设定的最大迭代次数，则t=t+1，返回至c.，继续计算循环迭代过程。

f.如果已到达设定的最大迭代次数，则判断是否达到温度终止条件，若未至冷却状态，则通过指定的降温方式冷却，并转至c.；若达到终止条件，则停止算法，输出的当前模型参数值为全局最优解。

4 Python-ABAQUS的模拟退火算法设计

Python作为计算机编程语言，拥有非常强大的面向对象的能力，在不同的平台上，用户可二次开发和编写脚本。

ABAQUS软件有效地使用Python脚本语言为使用者提供了许多库函数，实现有限元建模、单元网格划分、指定材料属性、提交作业和可视化后处理等操作。为了充分利用ABAQUS的二次开发功能，采用Python语言编写了(25+35+25)m双线连续轨道梁的全桥代码。模拟退火算法优化过程见图6。

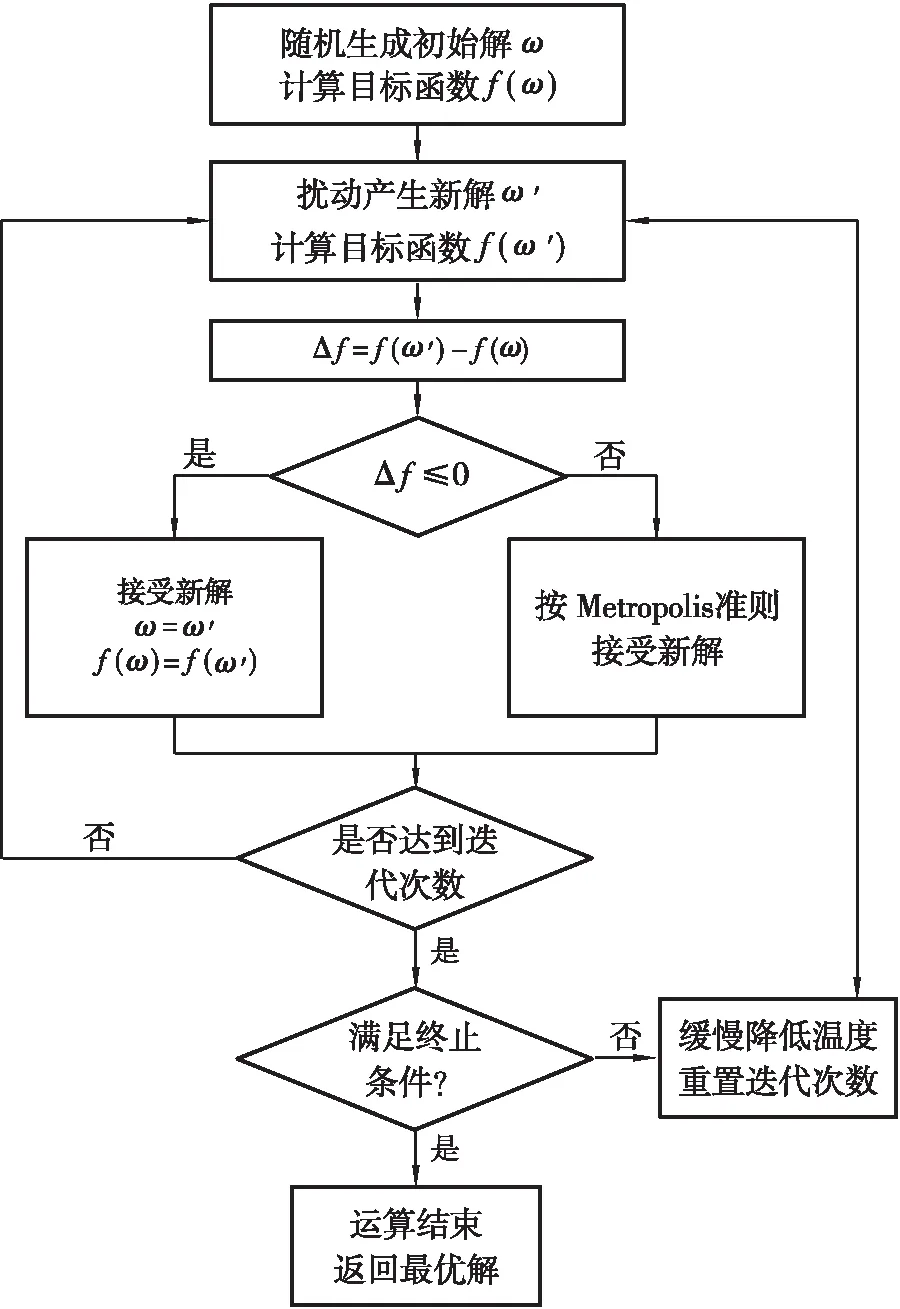
图6 模拟退火算法优化过程示意图解

a.确定设计参数。

利用ABAQUS设计敏感性分析程序计算得到箱梁主体、桥墩、承轨台、H型钢轨枕和F轨的相关材料参数对双线连续轨道梁前10阶固有频率的归一化敏感度，轨道梁动力特性的主要影响因素是箱梁和墩的质量，以及F轨的刚度，其他为次要因素。本次模型修正选用了5个设计参数，分别是箱梁、桥墩的密度和弹性模量，以及F轨的弹性模量，选取结果汇总见表2。

表2 设计参数表Table 2 Design Parameter Table材料性质弹性模量/MPa密度/(kg·m-3)箱梁3.55×1042 500桥墩3.40×1042 400F轨21.00×104—

b.选取状态变量。

对(25+35+25)m双线连续轨道梁，根据动力特性测试试验所得结果，取横向前3阶频率和竖向前3阶频率作为状态变量，汇总见表3。

表3 状态变量表Table 3 State Variable Table频率阶次实测值/Hz15.365竖向频率28.95039.85912.450横向频率23.33734.370

c.目标函数构造。

本文取计算频率和实测频率的相对误差平方和作为目标函数，使其取得最小值时所对应的设计参数值即为最优状态值，频率相对误差平方和可以表示为：

式中：λai，λti分别代表第i阶计算频率和实测频率。

d.算法设计。

① 初始温度。

在模拟退火过程中，要想较大可能性获得全局最优值，则可设定足够高的初始温度。然而，过高的初始温度往往导致数字较大的CPU时间。需要注意的是：模拟退火算法受启发于金属材料退火过程，其初始温度、退火温度、终止温度作为模拟退火的重要参数，并不像金属退火过程具有℃或K等单位。实际上，应根据以下条件选择初始温度：根据Metropolis判断规则初始温度时新的状态能量接受率(状态能量发生转移的粒子数与新的状态能量总数粒子总数)近乎100%；接受率随退火温度的降低逐渐降低，取为100 ℃。

② 温度衰减。

温度衰减对于模拟退火算法收敛性和CPU时间对于具有决定性作用。如果降温速率太慢，CPU时间数字较大，太快则易于得到局部最优。本文采用Kirkpatrick的几何温度衰减函数，温度衰减系数可在0.80～0.99范围内进行选择，取为0.98。

③ 终止规则。

模拟退火算法经常使用结束温度作为其终止准则，即当温度达到结束温度时退火过程终止。随着模拟退火，退火温度呈指数下降。实际上，温度会降到一个无限接近于0的值。此时，更小的状态能量难以出现，根据Metropolis判断规则目标函数难以获得更优值。以温度衰减系数为0.9时为例，温度从200降到0.0001将发生138次转移，足以获得全局最优方案，故本文中结束温度皆设为一个定值0.0001。

5 修正前后轨道梁结构动力特性结果对比分析

利用ABAQUS基于Python脚本接口的二次开发功能和设计敏感性分析的基本原理与方法，运用经验法选取了5个与结构动力特性直接相关且能直观反映桥梁实际状态的结构参数，并对其进行了敏感性分析。

通过比较分析箱梁主体、桥墩、承轨台、H型钢轨枕和F轨的相关材料参数对双线连续轨道梁前10阶固有频率的归一化敏感度，得出了轨道梁动力特性的主要影响因素为箱梁和桥墩的质量和刚度、F轨的刚度，对于轨道梁动力特性的影响，可以看出其他部分均为次要因素。

利用模拟退火算法与Python-ABAQUS相结合的有限元模型修正方法对影响(25+35+25)m双线连续轨道梁动力特性的主要设计参数在一定的可行域内进行了修正，经多次迭代过程，得到了最佳设计参数来，此时选定的目标函数取得最小值，修正前后的计算结果对比见表4、表5，部分振型见图7～图14。

图7 实测第1阶振型(f=2.450 Hz，横向)

图8 修正后第1阶振型(f=2.433 Hz，横向)

图9 实测第2阶振型(f=3.337 Hz，横向)

图10 修正后第2阶振型(f=3.294 Hz，横向)

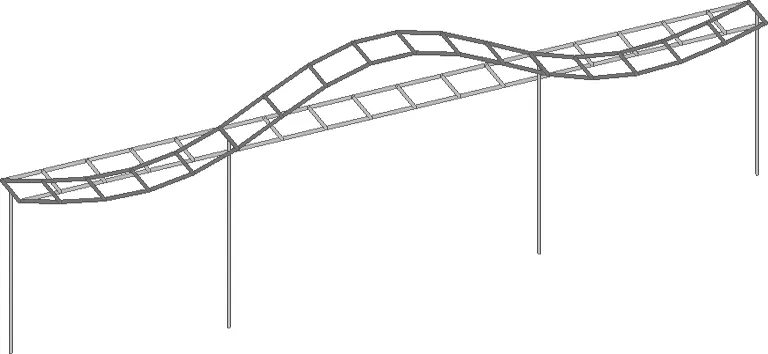
图11 实测第4阶振型(f=5.365 Hz，竖向)

图12 修正后第4阶振型(f=5.270 Hz，竖向)

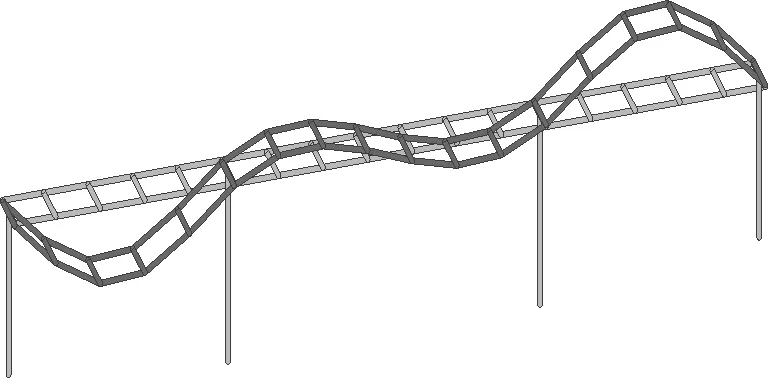
图13 实测第7阶振型(f=8.950 Hz，竖向)

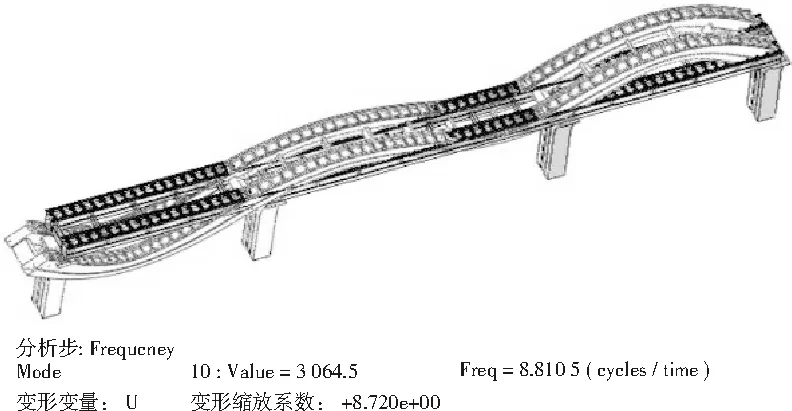
图14 修正后第7阶振型(f=8.811 Hz，竖向)

由上述分析结果可知，通过选取对轨道梁结构动力特性影响较大的5个主要设计参数，以计算频率和实测频率的相对误差平方和作为目标函数，利用模拟退火算法与Python-ABAQUS二次开发结合的有限元模型修正方法，成功地对(25+35+25)m双线连续轨道梁初始有限元模型进行了修正，其中参数变化值最大的为箱梁弹性模量，比初始有限元模型增加了15.2%，并与动力试验的实测频率和振型的对比结果表明，修正后的(25+35+25)m双线连续轨道梁模型能正确地反映结构的实际动力特性。

表4 修正前后各主要设计参数的变化对比Table 4 Comparison of changes in main design parameters before and after correction主要设计参数箱梁质量密度/(kg·m-3)箱梁弹性模量/MPa桥墩质量密度/(kg·m-3)桥墩弹性模量/MPaF轨弹性模量MPa修正前2 500.0003.550 0×1042 400.0003.400 0×10421.000×104修正后2 635.4524.089 6×1042 557.8253.693 1×10421.018×104参数变化5.42%15.2%6.58%8.62%0.09%

表5 修正前后前10阶实测频率与计算频率的对比Table 5 Comparison of the measured frequency and the calculated frequency of the first 10 steps before and after correction阶次实测频率/Hz修正前修正后计算频率/Hz误差/%计算频率/Hz误差/%振型描述12.4502.307-5.842.433-0.68横向弯曲一阶23.3372.996-10.223.294-1.28横向弯曲二阶34.3703.685-15.684.3870.39横向弯曲三阶45.3654.764-6.015.270-1.80竖向弯曲一阶55.4325.181-4.625.5251.72横向弯曲四阶66.7026.257-6.646.604-1.47横向弯曲五阶78.9508.249-7.838.811-1.56竖向弯曲二阶89.5368.888-6.809.422-1.20横向弯曲六阶99.8599.539-3.2510.0842.28竖向弯曲三阶1010.9509.918-9.4210.593-3.30扭转一阶

6 结论

本文提出了一种利用Python-ABAQUS二次开发结合模拟退火算法的有限元模型修正方法，并将这种方法应用于长沙磁浮交通工程(25+35+25)m双线轨道梁的空间有限元模型修正中，得到了较为理想的修正模型。主要研究结论如下：

a.通过敏感度分析，选取了对轨道梁结构动力特性影响较大的5个主要设计参数，选取计算频率和实测频率的相对误差平方和作为目标函数，利用模拟退火算法与Python语言结合的有限元模型修正方法，得到了使目标函数取得最小值时的最优设计参数，其中参数变化值最大的为箱梁弹性模量，比初始有限元模型增加了15.2%，变化最小的为F轨弹性模量，仅增加了0.09%。

b.通过修正前后的轨道梁动力特性与动力试验的实测频率和振型的对比结果表明，利用模拟退火算法与Python语言结合的有限元模型修正方法修正后的(25+35+25)m双线连续轨道梁模型能正确地反映结构的实际动力特性。