GR4J模型在钱塘江流域的适用性研究
2021-02-14张徐杰张发鸿赵建锋
张徐杰,张发鸿,富 强,赵建锋
(中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122)
0 引 言
水文模型是模拟自然界水文循环的数学物理模型,模型的输入数据一般包括降雨等,模型输出结果一般为径流。水文模型根据对流域的空间离散程度可以分为集总式水文模型和分布式水文模型。由于集总式水文模型具有结构简单、输入数据要求较低等优点,其应用程度并不亚于分布式水文模型。常见的集总式水文模型有斯坦福模型、水箱模型、新安江模型、萨克拉门托模型等[1]。
GR4J模型是来自法国的一个集总式水文模型,是由Perrin等人于2003年在GR3J模型的基础上开发而来的[2]。由于其简单实用的特性,GR4J模型在国外已被广泛地应用在水文模拟、洪水预报等相关研究中,并且取得了较好的效果[3-6]。而在国内,GR4J模型的应用还相对较少,主要有邓鹏鑫等[7]在赣江流域日径流模拟中的应用,管晓祥等[8]在黄河流域径流过程模拟的应用,王强等[9]在辽宁干旱半干旱流域的适用性研究等。
本文主要以钱塘江流域为研究对象,采用GR4J模型进行逐日径流模拟,对模型的模拟效果和适用性进行分析和评价,以进一步拓展GR4J模型在国内流域水文模拟中的应用。
1 GR4J模型原理
GR4J模型通过使用两个非线性水库进行产流汇流计算,分别称为产流水库和汇流水库,模型结构如图1所示[2]。模型中共有4个参数,分别是:产流水库最大蓄水量X1(mm)、地下水交换系数X2(mm)、前一天汇流水库最大蓄水量X3(mm)、单位线UH1的汇流时间X4(d)。下面对模型的产流和汇流过程作简单介绍。
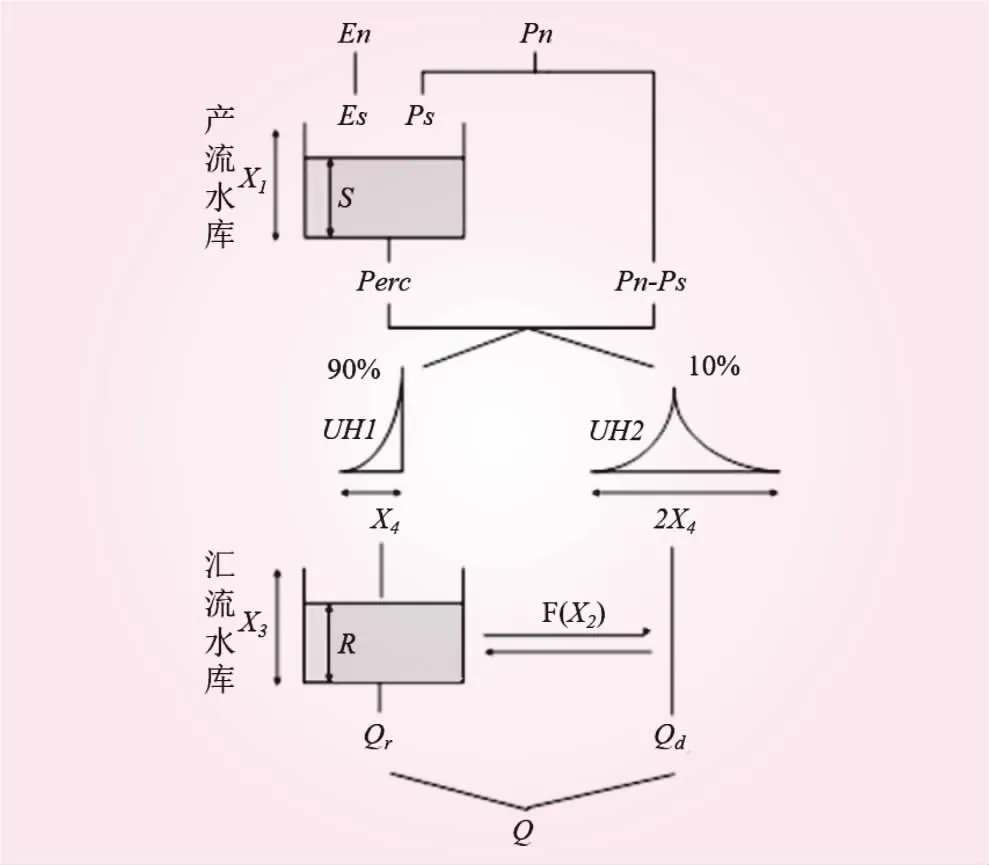
图1 GR4J模型结构示意
(1)产流阶段。GR4J模型中,首先根据模型的输入即降雨和蒸发(分别记为P和E,单位mm,下同),确定净降雨量Pn和蒸散发能力En。若P≥E,则Pn=P-E,En=0;若P
(1)
式中,S为产流水库的水量,mm;X1为产流水库最大蓄水量,mm。剩余部分为Pn-Ps,直接进入汇流阶段。当En>0时,产流水库的蒸发量Es由下式决定。即
(2)
然后,产流水库的水量S更新为
S=S-Es+Ps
(3)
则产流水库的产流量
Perc=s(1-[1+(4S/9X1)4]-0.25)
(4)
因此,产流阶段的总产流量
Pr=Perc+Pn-Ps
(5)
(2)汇流阶段。GR4J模型的汇流过程分为两部分,总产流量Pr的90%采用单位线UH1进行汇流演算,并经过汇流水库进行调节,剩余的10%采用单位线UH2进行汇流演算。两条单位线
UH1(i)=SH1(i)-SH1(i-1)
(6)
UH2(i)=SH2(i)-SH2(i-1)
(7)
式中,i为整数,表示第i天;SH1和SH2分别为单位线UH1和UH2对应的S累积曲线,计算式分别如下
(8)
(9)
式中,t为时间,d。模型中还考虑到这两部分汇流水量之间存在交换过程,交换量
F=X2(R/X3)3.5
(10)
式中,R为汇流水库的水量,mm。然后,汇流水库的水量更新为
R=max(0,Q9+F+R)
(11)
式中,Q9为经过单位线UH1演算后进入汇流水库的水量,mm。汇流水库的出流量
Qr=R{1-[1+(R/X3)4]-0.25}
(12)
经过单位线UH2演算和地下水交换水量汇合后的出流量
Qd=max(0,Q1+F)
(13)
式中,Q1为经过单位线UH2演算后的水量,mm。因此,流域出口总汇流水量
Q=Qr+Qd
(14)
2 模型应用
2.1 研究区域
钱塘江流域位于中国东部,东临东海,流域范围介于东经117°~122°与北纬28°~31°之间,流域面积约为5.56万km2。整个流域大部分位于浙江省西部,有南、北两源。其中,正源为北源新安江,发源于安徽省休宁县;南源兰江也发源于安徽省休宁县,源头海拔约为810 m。南源汇流后,向东南流入浙江省,至马金镇后称马金溪,再下行至常山港、衢州后称为衢江。衢江继续下行,在兰溪与金华江汇流后称为兰江。兰江干流长约303 km,流域面积约1.95万km2。由于新安江上有新安江水库影响天然径流过程,因此本次主要选取兰江流域作为研究区域,如图2所示。
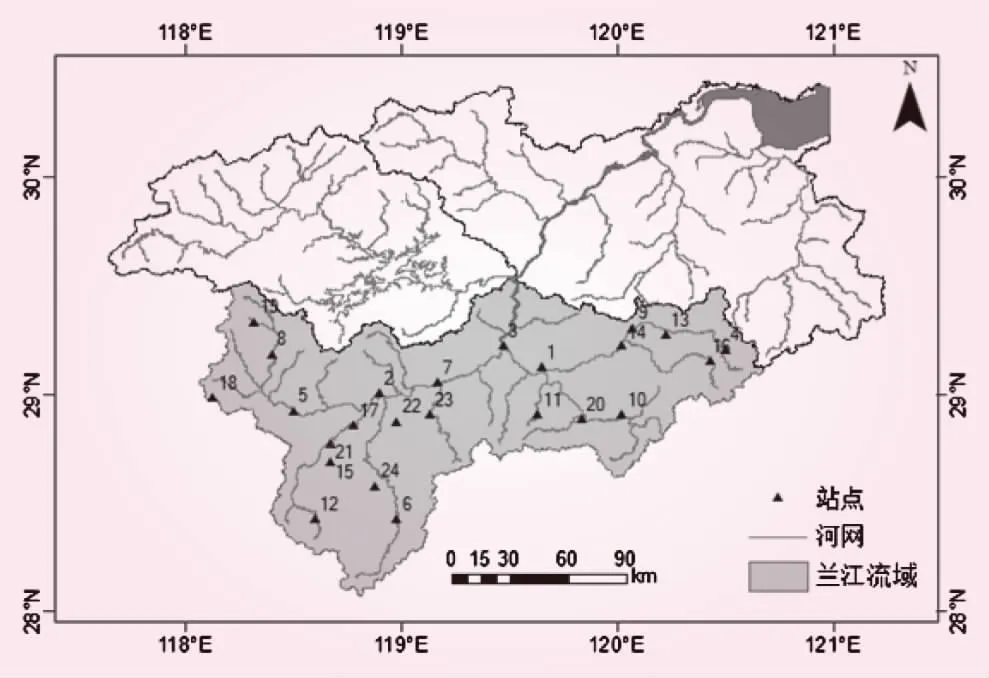
图2 兰江流域示意
2.2 基础数据
本文共选取兰江流域24个水文气象站点1980年~1990年的逐日观测资料进行分析计算。其中,流量站有6个,其逐日流量资料作为GR4J模型率定和验证的实测径流数据。气象代表站有2个,主要用于计算GR4J模型所需的潜在蒸发量。雨量站有23个,通过反距离权重插值后分别得到6个子流域对应的逐日降雨资料,作为模型输入数据。水文气象站点分布情况和基本信息见图2和表1。

表1 水文气象站点信息
3 结果与分析
采用兰江流域1980年~1990年的逐日水文气象数据,对GR4J模型的适用性进行研究和分析。其中,1980年作为模型预热期,1981年~1986年作为模型率定期,1987年~1990年为模型验证期。由于GR4J模型中只有4个参数,一般采用简单的率定方法就可以达到较理想的效果。因此,本文采用拉丁超立方体抽样法进行10 000组参数抽样,然后进行模型模拟,目标函数选用Nash-Sutcliffe系数。另外,还选用相对误差RBIAS来一起评价模型的模拟效果。即
(15)
(16)
式中,NS为Nash-Sutcliffe系数;RBIAS为模拟径流总量的相对误差;Qsim为模拟径流量,m3/s;Qobs为实测径流量,m3/s。
图3~图8是6个站点率定期和验证期的逐日模拟流量与实测流量对比图,表2和表3分别是GR4J模型在6个站点的参数率定结果和评价指标结果。结合以上图表可以看出,率定期和验证期NS系数均达到0.7以上,模拟径流总量的相对误差总体控制在±10%以内(除了金华站验证期为-11.26%)。对于流域面积较大的衢州、金华和兰溪3个站点,其NS系数均达到0.9以上,说明模型模拟效果总体较好。但从图3也可以看出,流域面积最小的密赛站,部分年份的峰值径流没有较好地模拟,说明GR4J模型在流域面积小的站点模拟效果不如流域面积大的站点。这可能是因为,在流域面积较小的山区,径流更加陡涨陡落,随时间的变异性更大,水文模型更加难以模拟。

表2 GR4J模型参数率定结果
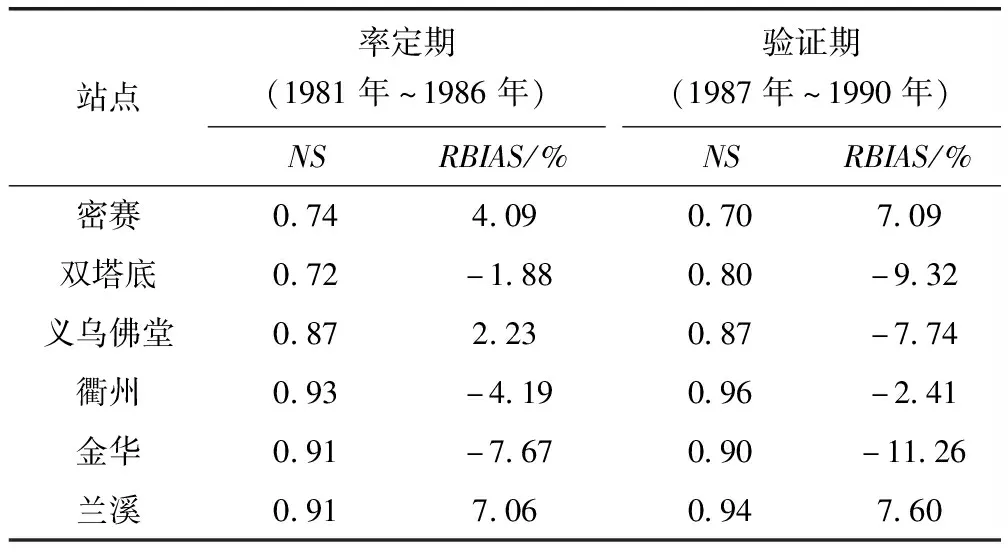
表3 模型率定期和验证期评价指标结果

图3 密赛站模拟和实测流量对比
图9所示的是6个站点10 000次模拟结果的NS系数分布情况。由图9可见,较大NS值(比如0.8以上)的频数并不是很多,这主要是因为本文对于模型参数率定采用了拉丁超立方体抽样法,在参数范围内进行了比较均匀的抽样,并没有参数迭代寻优的过程,导致较理想模拟结果的次数所占比例较小。对于流域面积较大的衢州、金华、兰溪3个站点,NS系数超过0.6的模拟次数基本超过50%,说明GR4J模型在兰江流域总体具体较好的适用性。
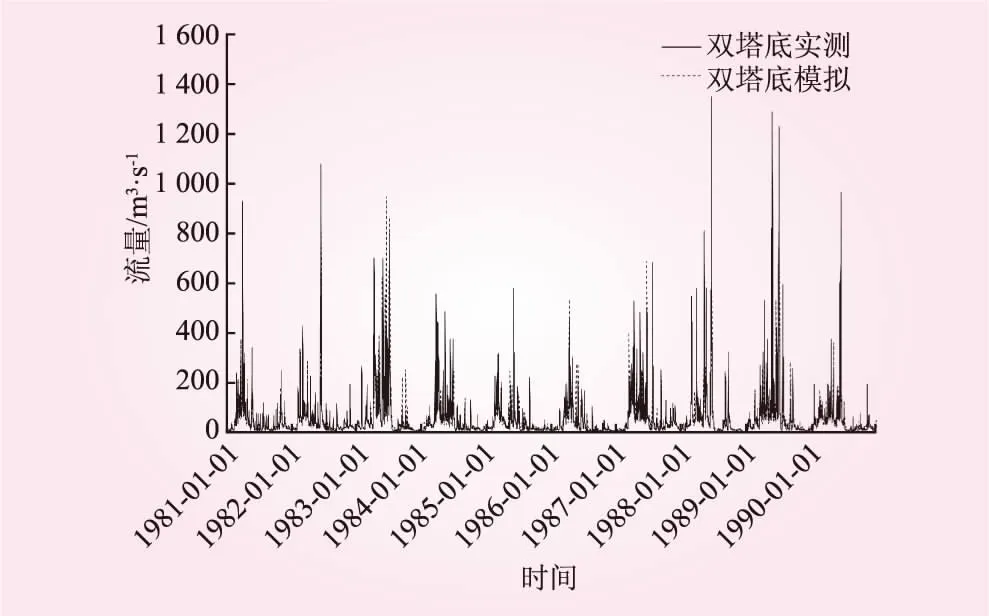
图4 双塔底站模拟和实测流量对比

图5 义乌佛堂站模拟和实测流量对比

图6 衢州站模拟和实测流量对比

图7 金华站模拟和实测流量对比

图8 兰溪站模拟和实测流量对比

图9 各站水文模拟NS系数分布情况
4 结论与展望
GR4J是一个结构简单的4参数集总式水文模型,目前在国内的应用不是特别普遍。本文采用GR4J模型,在钱塘江流域的兰江子流域进行应用。1981年~1990年的逐日径流模拟结果表明,6个水文站点率定期和验证期的最大NS系数均达到0.7及以上。其中,流域面积较大的3个站点,大概50%模拟次数的NS系数超过0.6,率定期和验证期的最大NS系数达到0.9及以上。模拟结果表明,GR4J模型在兰江流域总体具体较好的适用性。
本次研究的不足主要包括以下两个方面:一是参数率定的方法较简单,没有迭代寻优的过程;二是目前的参数率定结果表明,模型参数X3的推荐范围(推荐范围出自参考文献[2])可能需要进一步扩大(密赛站X3的率定结果在推荐范围的下限)。后续研究中,将进一步扩大部分参数范围,探究不同地区的参数差异性,并在参数率定方法上寻找其他更优方法的可能性。
