三平移刚柔混合并联机构优化设计与动力学分析

2021-02-14时宽祥沈惠平段恩业

农业机械学报 2021年12期

朱伟时宽祥王烨沈惠平段恩业

(常州大学机械工程学院，常州 213164)

0 引言

绳驱动并联机构[1](Cable-driven parallel mechanisms, CDPMs)是一种用绳索驱动代替刚性杆驱动的并联机构，它具有工作空间大、运动速度快、承载能力强、柔顺性好等特点。绳驱动并联机构CDPMs可分为欠约束CDPMs(nm+1)。由于绳索只能受拉，所以完全约束和过约束的CDPMs可以实现完全控制，而欠约束的CDPMs则需要增加辅助力来实现控制[2]。MING等[3]提出将重力看作虚拟驱动绳索，并从理论和试验上证实了欠约束CDPMs在重力作用下是可控的，此后，这一方法被广泛应用于欠约束CDPMs的驱动控制[4]。为了使并联机构只存在移动自由度，通常在支链中采用平行四边形结构，如经典的Delta[5]机器人，这种构型方式同样适用于CDPMs。BOSSCHER等[6]将平行四边形支链应用于CDPMs，提出一种平行绳索结构的欠约束绳驱并联机械手，这类由平行绳支链结构构成的CDPMs在运动中只要同组绳索与动、静平台的链接点构成平行四边形，则动平台的姿态始终不会改变[7]。VU等[8]在此基础上使用3组绳索构成3个平行四边形支链，机构动平台只能作空间平移运动，并且通过雅可比矩阵的奇异性确定了机构的工作空间。

相比刚性并联机构，CDPMs虽有上述诸多优点，但同时存在绳索张力不足、刚度较差[9]等缺点。为了改善绳驱并联机构的力学性能，BEHZADIPOUR等[10]提出通过增加刚性杆来改善CDPMs刚度，并通过构建等效弹簧的方法建立机构的刚度矩阵，结果表明这种方式可有效提高CDPMs的结构刚度。ZHANG等[11]在3自由度平行绳结构的CDPM中增加了一条中间弹性支链，不仅提高了绳索张力，使机构各组绳索在运动中分别保持平行，而且改善了机构运动性能。BEHZADIPOUR等[12]提出了一种类似“可变脊椎”的结构，用来提高CDPMs中的绳索张力。然而，在大多数CDPMs中，驱动绳索对动平台通常都存在力矩作用，给机构分析带来较大难度，GOSSELIN等[13]发明了空间交叉绳系(Crossing cables)结构，绳索拉力对动平台的合力矩为零，大大简化了力学分析难度，而且这种构型不会发生绳索干涉现象[14]，又增加了绳驱并联机器人的可达工作空间，具有很好的推广应用价值。

本文提出一种3自由度绳驱并联机构，在绳系为同组平行异组交叉的CDPMs基础上，增加一被动弹性支链，分析机构的运动学方程、可达工作空间和任务工作空间；在动平台具有高加速度的前提下，以驱动绳索的驱动力为优化目标对弹簧参数进行优化；建立拉格朗日动力学方程，通过和期望运动轨迹对比，验证其正确性和合理性。

1 机构设计

机构原理如图1a所示，由静平台、动平台以及连接于二者之间的3组平行绳索(6根绳索)和中间弹性可伸缩支链组成。3组平行绳索一端(绳①、②为组1，绳③、④为组2，绳⑤、⑥为组3)穿过固定在静平台上的3组导向套A1A2、A3A4、A5A6上，同组平行绳索另一端连接于动平台的圆周上，连接点分别记为B1和B2、B3和B4、B5和B6，且B1B2、B3B4、B5B6的连线均经过动平台圆心O，两两之间的夹角为60°，如图1b所示。中间弹性可伸缩支链两端分别通过U副连接于静、动平台中心点O和点P，该支链可以看作SPS型弹性支链(S表示球副，P表示移动副)。由于弹簧作用，中间支链始终处于被压状态，3组平行绳索则保持张紧，它们与静、动平台的连接点构成了平行四边形结构A1A2B1B2、A3A4B3B4、A5A6B5B6。因此，动平台在运动中姿态保持不变，即机构只能实现三平移运动，故记为3T绳驱机构(T表示移动副)。

机构结构设计如图1b和图2所示。驱动电机位于A2i-1A2i(i=1,2,3)的中间位置Ci(i=1,2,3)处，电机带动绞盘旋转从而同时驱动两根平行绳索A2i-1B2i-1和A2iB2i运动，如图2b所示。中间弹性可伸缩支链由移动杆、导向杆和安装于两者之间的弹簧组成，刚性杆不仅有导向作用，还可以限制弹簧的伸缩范围，其结构如图2c所示。绳索布置方式采用同组平行、异组交叉的结构，如图2d所示。

2 运动学分析

2.1 位置与速度分析

如图3所示，在静平台中心点O建立机构的固定坐标系Oxyz，OC1方向为固定坐标系的x轴正方向，Oxyz的z轴正方向为垂直向下。由于机构只存在空间三平移运动，动平台中心点P的位置在固定坐标系中可表示为

p=lOP=(x,y,z)

(1)

由于机构中6绳索构成3组平行绳索,所以对机构进行运动分析时，可以将每组平行绳索分别简化成一条由点P到点Ci之间的虚拟的中间绳索，如图3所示，记lPCi=ρi(i=1,2,3),则ρi=lB2i-1A2i-1=lB2iA2i。

根据封闭矢量原理可建立机构位置方程

p=ci-ρi(i=1,2,3)

(2)

式中ci——第i个电机Ci(绞盘)在固定坐标系中的位置矢量

根据图1b可知

(3)

其中

c1=[R0 0]T

式中R——静平台基圆半径

R1、R2、R3——固定坐标绕z轴转动的变换矩阵，旋转角分别为0°、-120°和120°

将式(3)代入式(2)可得运动方程

Ric1-p=ρi

(4)

所以3T绳驱机构的位置方程为

‖Ric1-p‖=‖ρi‖ (i=1,2,3)

(5)

设被动弹性支链p的单位向量和第i组虚拟中间绳索矢量ρi的单位向量分别为up和ui，则up=p/‖p‖,ui=ρi/‖ρi‖。将式(2)两边对时间求导可得

(6)

式中ρi——第i组中间绳索矢量ρi的长度

对式(6)两边点乘单位向量ui，进一步得到各组绳索的速度为

(7)

因为6条绳索构成3组平行四边形绳索结构，所以绳索速度和动平台速度可以表示为

(8)

J——机构雅可比矩阵

2.2 工作空间分析

绳索并联机构在运动过程中弹簧一直处于被压缩状态(保持弹性)，但弹簧被压缩量有限。通常情况下弹簧最大压缩量不超过初始长度的50%[15]，则中间弹性可伸缩支链的长度p的范围为

pmin≤p≤pmax

(9)

其中

pmin=0.5LS+Spmax=LS+S

式中pmin、pmax——中间弹性可伸缩支链的最小和最大长度

LS——弹簧初始长度

S——导向杆长度，如图2c所示

考虑到中间弹性支链的尺寸以及球铰的约束，设弹性支链的摆动范围为[-π/4,π/4]，动平台最大运动空间的几何形状如图4所示。对于CDPMs，其工作空间的确定还要考虑驱动绳索是否受拉。设每条绳索的拉力为tj(j=1，2，…，6)，因同组平行绳索中两绳索的拉力相同，故3组平行绳索的等效拉力矢量可表示为Ti=Tiui=2t2i-1=2t2i(Ti为第i组平行绳索的拉力,i=1,2,3)，由于绳索只能承受单向力，所以机构在工作空间内任意位置时，各组绳索的拉力Ti必须为正(方向同ui)，否则该位置点不在机构的工作空间内[16]。如图5所示，机构动平台同时受到3组平行绳索的等效拉力Ti、中间支链弹性力Fk和动平台重力G的作用，弹簧弹力沿着中间支链向下。根据静力平衡原理建立动平台力平衡方程

T1+T2+T3+Fk+G=0

(10)

其中

Fk=k(LS+S-p)upG=mg

式中m——动平台质量

g——重力加速度向量

k——弹簧弹性系数

绳索拉力Ti、弹簧弹力Fk和动平台重力G在空间中汇交于动平台的质心点P，且构成封闭矢量，由文献[17]可知，只要弹簧弹力Fk向下(弹簧受压)，则式(10)中各组绳索拉力Ti都一定平行于第i组绳索且方向向上，即拉力为正。所以，机构可达工作空间[18]的几何形状如图5所示。

考虑到实际应用，设定动平台的任务工作空间[17]几何形状为一规则的圆柱体，如图5所示。设该圆柱体直径D与高H的比为4∶1，则可建立几何关系

(11)

联立式(9)、(11)可得

(12)

设当中间支链与固定坐标系Oxyz的z轴重合，且动平台位于任务工作空间的下底面时，动平台对应的位置为机构的初始位置，对应的高度为初始高度h，且由图4a可知h为

h=pmin+H

(13)

基于以上分析可知，绳索拉力、机构可达工作空间、任务工作空间与中间支链的长度p有关，而中间支链的长度p又取决于弹簧的初始长度LS。

3 中间支链优化设计

3.1 参数优化

为了满足高加速度及一定的任务工作空间的要求，机构弹簧参数确定需要同时从3方面来考虑：① 绳索拉力必须大于等于允许最小张力fmin。② 保证机构在具有高加速度的状态下，驱动绳索的驱动力较小，能量消耗较小。③机构能够达到期望的任务工作空间。需要注意的是，动平台在高速运动时，由于机构存在弹簧，所以会产生弹性振动，进而影响机构的运动精度和稳定性。为了减轻弹簧的弹性振动，一方面设计弹簧直径与刚性移动杆的直径近乎相等；另一方面，弹簧在机构工作过程中始终处于被压状态。由前面的分析可知，中间弹性支链不仅影响动平台的工作空间，而且支链中的被压弹簧对机构的绳索张力、加速度及驱动力都有很大的影响。若中间支链中导向杆长度S已确定，则弹簧就决定了中间支链结构，而影响弹簧特性的主要有两个参数：弹性系数和初始长度。

根据机构结构，设置机构部分参数如表1所示。

设弹簧弹性系数和初始长度分别为k和LS，根据达朗贝尔原理求得绳子拉力需满足

UT=maε-Fk-mg (14)

其中U=[u1u2u3]T=[T1T2T3]T

式中T——绳索拉力向量

a——动平台(质心)加速度

ε——动平台加速度方向的单位矢量

因为u1、u2、u3为线性无关的列向量，所以U存在逆矩阵U-1，则绳索拉力可表示为

T=U-1(maε-Fk-mg)

(15)

由机构位置方程式(2)、(3)可得

ρ1u1+ρ2u2+ρ3u3=(c1+c2+c3)-3p=-3p

(16)

两边同时点乘Fk后，整理可得

-3U-1Fkpup=[Fkρ1Fkρ2Fkρ3]T

(17)

其中

Fk=k(LS+S-p)

将式(17)代入式(15)可得

(18)

由式(18)可求T的分量Ti为

(19)

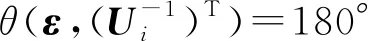
(20)

对式(20)两端所表达的集合取并集，即可得到当机构在工作空间内运动加速度为a时，绳索可能的最小和最大拉力为

(21)

(22)

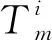
(23)

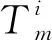
将式(23)所表达的动平台位置在任务工作空间中表示，如图6所示。

当给定动平台一个加速度，则绳索驱动力与弹簧参数的关系可以由式(2)、(3)和式(19)～(22)确定。为了使机械手能够高速运动，设式(14)中动平台任意方向的加速度为5g。当动平台在任意位置的任意方向都具有5g加速度时，则被动弹性支链中弹簧弹性系数k、初始长度LS和绳索驱动力Tmin、Tmax之间的关系如图7所示。

设定本机构中每组平行绳索的最小张紧力fmin为10 N，因为绳索必须处于张紧状态，即拉力不小于最小张紧力，所以弹簧的参数必须在Tmin≥10 N的区域中选择。从图7可以看出，同一初始长度(弹性系数)下，Tmin/Tmax等值线的值越大,绳索拉力就越大，即所需要驱动力越大，所以选择Tmin=10 N的等值线。此时，绳索在满足最小张力的条件下，动平台达到加速度5g所需要的绳索最小驱动拉力为10 N。在Tmin=10 N的等值线上，若初始长度LS选择越大，则绳索拉力的最大值Tmax就越大，即所需要绳索的驱动拉力越大。从式(12)可知，若初始长度LS减小，则机构的任务工作空间就会缩小。考虑到机构的实际应用，设定期望的任务工作空间的高度H≥0.25 m，则弹簧初始长度必须满足LS≥0.56 m。因此综合考虑，弹簧初始长度LS可选为0.6 m，此时弹簧弹性系数k为1 300 N/m，如图7所示。从图7可以看出，当LS=0.6 m、k=1 300 N/m，若动平台在工作空间内以加速度5g运动时，绳索的驱动力(拉力)的最小值和最大值分别为10 N和280 N。此时，由式(13)可得，机构初始高度h为0.95 m。图8为弹簧参数优化设计流程图。

3.2 性能估计与验证

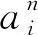
(24)

式中，Tmin=10 N。

将上面优化后的弹簧参数LS、k和初始高度h代入式(24)，可以得到动平台的加速度a为

(25)

(26)

式中，Tmax=280 N。

此时，动平台对应的加速度a为

(27)

根据上述优化结果，选取弹簧参数:LS=0.6 m,k=1 300 N/m,且每组绳索拉力Ti=10 N和Ti=280 N时,机构在工作空间内任意位置的加速度，结果如图9所示。从图9可以看出，在驱动绳索拉力为10 N和280 N时，机构动平台的最大加速度分别为288.6 m/s2和217.4 m/s2，最小加速度分别为50.4 m/s2和49.7 m/s2。显然，优化后弹簧参数使动平台加速度达到期望的5g加速度，可以实现高速运动。由此，可以认为弹簧参数的优化方法和结果合理。机构参数分别为k=1 300 N/m，LS=0.6 m，h=0.95 m。

4 动力学分析

4.1 动平台动力学模型

在CDPMs中，3T机构主要有动能和势能两种能量，可以考虑采用拉格朗日方法建立动平台的动力学模型。动平台质量为m，轻质刚性伸缩杆质量为mr，绳索质量忽略不计,建立如图3所示的坐标系。根据拉格朗日法，建立机构动力学方程为

(28)

其中L=Ek-Ep

式中q——广义坐标向量

L——拉格朗日函数Ek——机构动能

Ep——机构势能(包括重力)，取Oxy平面是零势能面

Q′——广义坐标对应的广义力向量(非保守力引起的)

根据图2、3，推导得基于广义坐标q的机构动能和势能为

(29)

(30)

则拉格朗日函数L为

(31)

求解广义力的方法有矢量定义法和广义虚位移法，这里采用后者。由虚位移原理求解广义力为

(32)

式中qj——机构第j个广义坐标

Q′j——非保守力对应于qj的广义力

δW——绳索拉力所作的虚功

将q1=x,q2=y,q3=z代入式(32)得

∑δW=Q′1δx+Q′2δy+Q′3δz

(33)

因为δqj具有任意性，所以设δx≠0,δy=δz=0，则机构绳索拉力所作的虚功为

∑δW=T1δx+T2δx+T3δx

(34)

即Q′1δx=T1δx+T2δx+T3δx

(35)

则由式(35)可计算

(36)

同理，分别设δy≠0,δx=δz=0和δz≠0,δx=δy=0，则有

Q′2δy=T1δy+T2δy+T3δy

(37)

Q′3δz=T1δz+T2δz+T3δz

(38)

将式两边分别同除以δy和δz可得

(39)

(40)

式中Q′1、Q′2、Q′3——广义向量Q′中的元素

i、j、k——笛卡尔坐标系的x、y、z轴的单位矢量

U1、U2、U3——U的第1、2、3行元素

根据3T绳驱机构工作空间的几何关系,可得到广义坐标向量q的范围为

Nl≤qT[ijk]≤Ml

(41)

其中

将式(31)、(36)、(39)、(40)代入式(28)可得

(42)

将式(42)改写成矩阵形式，并联立式(41)即可得动平台的动力学模型为

(43)

Q=[-Q′1-Q′2-Q′3-mg-mrg/2]

4.2 仿真验证与分析

在机构的动力学模型中，机构参数如表1所示。设动平台期望轨迹方程为

(44)

由式(44)可知，动平台的期望运动为空间运动：动平台先由初始位置z=0.95 m垂直向上运动至z=0.8 m处，停滞0.2 s再沿x轴正方向水平运动0.2 m，再停滞0.2 s后在该水平面上作半径为0.2 m的圆周运动。

已知动平台的运动轨迹求驱动力是动力学反解问题[20]。将动力学模型式(43)的Matlab数值计算结果和ADAMS的虚拟样机仿真结果进行对比，结果如图10所示。由图10可以看出，Matlab数值计算结果与ADAMS仿真结果基本一致，验证了动力学模型的正确性。

5 试验

基于中间支链结构优化后的结果，设计并搭建了3自由度绳驱动并联机构的试验样机(图11)。

在抓取、分拣等领域中，绳驱并联机器人的主要操作就是在机器人可以达到的三维空间中，实现某一点到另一点的抓取和放置操作(Pick and place operations，PPO)[21]，故假设动平台期望轨迹为“门”字形轨迹，包括拾取、搬运、放置三过程，如图12所示。其中，设定6个路径点，记为Nh(h=1,2,…,6)；表2为它们的坐标位置。为实现这一轨迹，动平台需依次完成上升阶段N0N2、水平运动阶段N2N4以及下降阶段N4N6。