四轮独立驱动高地隙无人喷雾机轨迹跟踪自适应控制

景 亮 张亚飞 沈 跃 何思伟 刘 慧 崔业民

(1.江苏大学电气信息工程学院， 镇江 212013； 2.南通广益机电有限责任公司， 南通 226631)

0 引言

农机自主导航技术是农机自动化、智能化的关键技术之一，可显著提高作业质量和生产效率[1]。目前，农机自主导航已广泛应用于耕作、播种、施肥、喷药、收获等农业生产过程[2]。

农机自动导航包括导航位姿信息获取、导航路径规划和导航控制[3-4]，其中导航控制算法是导航系统的核心。而农机自身大延迟、大惯性和高度非线性的特征要求导航决策控制算法具备一定的自适应性和鲁棒性[5-6]。目前国内外常用的农机导航控制方法包括 PID控制、模糊控制、纯追踪控制、滑模变结构控制、最优控制和模型预测等[7-10]。已有研究均假设农机作业过程中满足理想的“非完整约束条件”，即农机在行驶过程中轮胎始终保持“纯滚动无滑动”的状态[11]，然而农机的作业环境复杂多变，由于各种因素，如轮胎打滑、变形等，纯滚动约束不可能得到严格满足，特别是当农机需要在水田、坡地、湿滑草地等地面上行驶时，不可避免地发生侧滑，进而影响农机自主导航的性能，甚至影响系统的稳定性[12]。

目前对车辆侧滑的相关研究较少。文献[13]研究了车轮打滑情况下农用车辆的轨迹跟踪控制，同时也考虑了侧滑角对导航精度的影响，结果表明农机轨迹跟踪的精度会受到车轮打滑的影响，该研究在模拟仿真环境中进行了测试，并未在实际车辆上实现。文献[14]提出了一种结合了高精度定位系统(RTK-GPS)的侧滑角观测器并将其集成到系统模型中，在试验中手动驾驶农用拖拉机，并用(RTK-GPS)记录路径，然后估算模型的参数, 估算结果较为准确，为复杂环境下农机自动导航研究提供了思路。文献[15]针对果园自主导航车辆的轨迹跟踪问题，提出了一种侧滑估计器，采用高精度定位系统(RTK-GPS)估计车辆作业时的纵向和横向滑移速度，提高了果园自主导航车辆的轨迹跟踪性能，但该研究只考虑了车辆的横向控制。本文研究工作场景主要为水田、草地的四轮独立驱动(Four wheel independent drive，4WID)高地隙喷雾机的轨迹跟踪问题。设计一种结合自适应方法与反步控制方法的轨迹跟踪控制算法。首先建立侧滑情况下高地隙喷雾机运动学模型，然后基于此模型设计自适应控制器，通过参数自适应来补偿未知侧滑效应。最后在考虑侧滑与不考虑侧滑两种情况下分别进行仿真和水田试验。

1 四轮独立电驱动运动学建模

高地隙四轮独立电驱动喷雾机的转向结构与传统阿克曼以及差速转向结构不同，转向结构的3D模型如图1所示，主要由车架和前、后转向桥3部分组成，每个转向桥通过平面轴承与车架前后转向中心联接，车辆动力来自4个独立的大转矩轮毂电机，每个电机的转矩均可独立控制，因此无需额外转向动力就可以通过协同控制4个轮毂电机的转速完成直行与转向作业[16]。为保证同步转向以及提高转向桥的抗干扰性能，通过建模与计算在前后轴之间安装了两个辅助连杆[17]。

1.1 运动学模型

喷雾机运动学模型如图2所示，前后转向桥通过连杆约束，确保前后转向桥同步转向。首先建立全局坐标系XWY与车体坐标系xoy，A、B分别为前后转向中心，L为前后转向中心距离，D为转向桥长度，v为喷雾机线速度，δ为前后转向桥转角，θ为喷雾机在全局坐标系XWY中的航向，C为转向中心，定义逆时针旋转为正。设喷雾机左前轮、右前轮、左后轮、右后轮速度分别为v1、v2、v3、v4。由三角函数关系可得转向桥转向半径为

(1)

偏航角速度为

(2)

在喷雾机转向的动态过程中，喷雾机每个车轮的速度由底盘绕转向中心点C的速度与前后转向桥绕各自转向中心点A、B的速度合成，即

(3)

将式(2)代入式(3)得出四轮速度与喷雾机线速度、前后轴转角的关系式为

(4)

为进一步验证上述所建立数学模型的正确性，使用UG软件绘制等比例喷雾机3D模型并进行运动学仿真，仿真时设置目标车速和转向角并通过式(4)计算得到的四轮轮速输入到3D模型中，设置目标速度为3.6 km/h，最大转向角为25°，在UG软件中喷雾机仿真结果如图3所示，蓝色虚线为其行走轨迹。可以看出该转向结构不仅转向半径小而且同侧前后轮轨迹几乎重合，在实际的农田应用场景中可减少对农作物的损伤。

由于前后转向轴之间安装了辅助连杆，假设前后轴同步转向且转角一致，为简化计算过程，基于文献[18]中的运动学模型简化原理，将四轮模型转化为二轮车模型，如图4所示。

由图4可以看出，二轮简化模型的转向中心和运动规律与四轮模型一致，且二轮模型运动轨迹与喷雾机质心运动轨迹重合。因此以喷雾机质心为基准点建立简化的运动学模型

(5)

式中P——喷雾机质心在全局坐标系下的位姿

1.2 位姿误差模型

基于运动学简化模型建立如图5所示的位姿误差模型，o、or分别为喷雾机质心与参考质心，(xr,yr)为参考喷雾机质心or在坐标系XWY中的坐标，(x,y)为喷雾机质心o在坐标系XWY中的坐标，(xe,ye)为向量loor在坐标系xoy中的坐标，c(s)为目标路径的曲率，s为从初始位置沿着目标路径的点or的曲线坐标，θ、θr分别为喷雾机中心线相对于惯性坐标系的航向与参考航向，θe为航向误差，v、vr分别为喷雾机相对于惯性坐标系的速度与期望速度，vy为喷雾机横向速度，δb为喷雾机转向偏差。

轨迹跟踪控制器的目标即设计合适的控制律使得

(6)

利用坐标变换将全局坐标系下误差转换为喷雾机质心坐标系下误差Pe，计算式为

(7)

(8)

喷雾机参考角速度为

(9)

将式(7)两边分别对时间求导得到理想位姿误差模型为

(10)

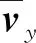
此时喷雾机纵向速度与横向速度满足约束

(11)

角速度满足约束

(12)

(13)

2 控制律设计

轨迹跟踪控制系统结构如图6所示，来自RTK的实时位姿信息、目标路径信息和期望速度作为控制器的输入以及侧滑估计数据源，控制器通过融合侧滑估计结果分别输出喷雾机目标速度vc以及目标转角δc实现轨迹跟踪控制。为验证侧滑估计的有效性，分别基于理想位姿误差模型以及改进位姿误差模型设计控制律并对比分析。

2.1 基于理想位姿误差模型的控制律设计

目前针对非线性系统大都采用级联形式的控制方法，其中链式系统法[19]以及反步控制方法[20-21]的应用最为广泛。其中反步控制方法可以通过反向设计使控制律的设计过程系统化、结构化，还可以控制相对阶为n的非线性系统，消除了经典无源性设计中相对阶为1的限制[22]。喷雾机位姿误差模型是一种复杂的非线性系统，首先使用反步控制方法设计基于理想位姿误差模型的控制律。

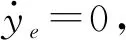
(14)

(15)

(16)

式中kx、ky、ku——正常数

2.2 基于改进位姿误差模型的控制律设计

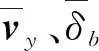
(1)选取正定Lyapunov函数

(17)

Γ——侧向滑移速度估计误差的控制参数

式(17)两边分别对时间求导并将式(13)代入可得

(18)

选取u1=sinθe作为第1步的虚拟输入，为保证ye收敛，取u1目标值计算式为

(19)

选取目标车速

vc=vrcosθe+kxxe

(20)

选取横向滑移加速度

(21)

式(19)与式(20)中ky、kx均为正常数，将式(19)～(21)代入式(18)可得

(22)

(2)定义u1与u1d之差

(23)

构建扩展Lyapunov函数

(24)

γ——转向偏差估计误差的控制参数

式(24)两边分别对时间求导可得

(25)

选取u2=tanδ作为第2步的输入，将式(12)、(13)和式(23)代入式(25)并简化

(26)

其中

α=c(s)vrcosθe+yevr+kysinθe

(27)

(28)

(29)

选取侧滑参数微分值为

(30)

(31)

选取目标转角正切值u2为

(32)

式(32)中ku为任意正常数，将式(30)～(32)代入式(26)可得

(33)

(34)

运用Lasalle定理[24]得，所有的解都收敛于

(35)

(36)

3 仿真验证

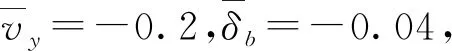
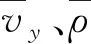
4 试验验证

高地隙喷雾机导航系统如图9所示，主要由高地隙喷雾机、厘米级高精度定位系统RTK、英特尔微型主机和4G路由器等构成。喷雾机上设有由28.5 kW汽油发电机和72 V蓄电池组成的油电混合的供电系统，在启动汽油发动机的情况下，喷雾机可以连续工作12 h。运输状态下喷雾机质量、长度、宽度、高度和轴距分别为1 680 kg、3 200 mm、1 760 mm、2 400 mm和1 680 mm。离地间隙1 100 mm；工作状态下喷雾机载药500 L，喷杆可展开至11 200 mm。

为获得更精准的位置以及航向信息，GNSS双天线的安装位置基线与喷雾机前进方向垂直，其中RTK用于获取喷雾机位置信息，作为滑移参数估计数据；移动路由器形成的局域网络实现远程端实时监测导航作业；微型主机与整车控制单元(Vehicle control unit，VCU)之间的信息交互借助RS485总线实现；喷雾机车轮以及前后转向桥中心分别安装了霍尔传感器和角度传感器，VCU采集实时轮速和转向角度信息作为反馈信息，电压巡检仪用来获取喷雾机实时电压。

微型主机装载了Ubuntu以及第二代机器人操作系统(Robot operating system，ROS2)，其中ROS2是一个专门针对机器人软件开发而设计的通信框架，能够满足导航控制系统的安全性、可扩展性和容错性要求[25]。使用C++语言编写ROS2导航算法节点、喷雾机节点与上位机界面节点，导航作业时在远程端运行上位机界面节点实时监测喷雾机状态并发布目标路径信息，再运行导航算法节点订阅来自传感器的各种信息，并将计算后的控制指令发布出去；最后运行喷雾机节点订阅导航节点发布的控制指令实现导航作业。

为进一步研究侧滑对轨迹跟踪性能的影响，验证本文轨迹跟踪算法的有效性。在海安市1.3 hm2泥泞水田中，分别使用考虑与不考虑侧滑的控制律进行轨迹跟踪试验。为保证试验数据的有效性，规划目标轨迹为两段U形轨迹(由3条直线与2条曲线组成)。喷雾机展开喷杆后喷幅为12 m，因此设置地头转向半径为6 m，根据地块尺寸设置直线段长度为55 m。期望车速为3.6 km/h，由于本文控制器跟踪的量为动态的位姿信号，在进行参数调节时先在校内水泥地平整路面设定一个目标点让喷雾机单独去跟踪并记录控制器输出信号与轨迹跟踪误差信号，在进行参数调节后跟踪效果良好的情况下，将该参数应用到水田U形路径的跟踪控制中，再根据喷雾机跟踪效果进行微调，最终选择一组跟踪效果较好的控制参数kx=0.1，ky=0.6，ku=0.05，Γ=0.1，γ=0.05。试验现场如图10所示。

校正前后的轨迹跟踪如图11所示。由图11a可以看出，当喷雾机跟踪的目标路径在由直线变为曲线的开始与结束时侧滑效应较为明显，而直行时侧滑效应影响较小，但仍会引起小范围的震荡。由于考虑了侧滑效应，图11b中的轨迹跟踪效果更好。

校正前后横向、纵向以及航向误差如图13所示。图中分别标注了直线部分与曲线部分的试验结果，可以看出试验结果与仿真结果基本一致。

校正前后横向、纵向以及航向误差结果如表1所示。由表1可知，侧滑效应对横向跟踪精度以及航向跟踪精度的影响较为明显，对纵向控制精度几乎没有影响。在不考虑侧滑的情况下，喷雾机最大横向误差为0.287 m，平均绝对横向误差为0.114 m，标准差为0.13 m；最大纵向误差为0.069 m，平均绝对纵向误差为0.019 m，标准差为0.019 m；最大航向误差为14.56°，平均绝对航向误差为4.55°，标准差为5.54°。考虑侧滑后，侧滑效应的影响减弱。喷雾机最大横向误差减小为0.167 m，平均绝对横向误差减小为0.041 m，标准差减小为0.059 m；喷雾机纵向控制误差几乎没变化；喷雾机最大航向误差减小为11.97°，平均绝对航向误差减小为2.56°，标准差减小为3.57°。

校正前后控制转角如图14所示。校正前的控制器未考虑侧滑进而导致轨迹跟踪时累计误差较大，为跟踪到目标轨迹，控制器所输出的控制转角信号波动较大，而校正后的控制器由于考虑了侧滑，所输出的控制转角信号更为平滑，对转向机构更为友好。

5 结论

(1)针对4WID高地隙喷雾机特殊的转向模型，建立了该喷雾机的运动学模型并在UG软件中仿真验证所建立模型的准确性。

(2)建立了喷雾机轨迹跟踪的理想位姿误差模型以及考虑侧滑因素的改进位姿误差模型，并分别设计轨迹跟踪控制器。以典型U形路径为例，对两种控制器进行了仿真验证。结果表明，当模型中未加入侧滑影响时，两种控制器均可以保证喷雾机快速跟踪到目标轨迹，跟踪精度较高；当考虑侧滑影响时，自适应控制律能够实时估计并补偿侧滑参数，跟踪轨迹误差更小，控制效果更好。

(3)田间试验结果表明，考虑侧滑后的轨迹跟踪最大横向误差减小为0.167 m，平均绝对横向误差减小为0.041 m，标准差减小为0.059 m；最大航向误差减小为11.97°，平均绝对航向误差减小为2.56°，标准差减小为3.57°。因此，在水田等复杂的作业环境下，加入侧滑参数的模型更加贴合农机实际的运动规律，基于该模型设计轨迹跟踪控制律能够有效提高农机导航精度和自动驾驶的稳定性。