基于干扰观测器的直播机路径跟踪快速终端滑模控制

武 涛 李彦明 林洪振,2 贡 亮 刘成良,2

(1.上海交通大学机械与动力工程学院， 上海 200240； 2.机械系统与振动国家重点实验室， 上海 200240)

0 引言

在土壤特性复杂多变，高度非结构化的水田环境下，农业机械(农机)本身会受到许多不确定性因素干扰，这给智能农机精确地按照既定轨迹自动驾驶带来了极大困难。要求使用的控制算法具备一定抗干扰和自适应能力，才能保证农机自动驾驶具有较高的精度和稳定性。

国内外学者在农机自动驾驶路径跟踪控制算法上已进行了广泛研究[1-2]。主要集中在建立农机的运动学[3-9]、动力学[10-14]或纯追踪模型[15-18]，以及常用的模糊控制[19-22]、PID控制[23-25]、最优控制[26]和滑模控制[27-30]等控制方法上。由于运动学模型简单高效，对参数精确度要求较低，因此将农机简化为二轮车，用一些状态变量描述农机位置和姿态能建立较为准确的农机运动学模型。文献[3，5]较早建立了拖拉机的二轮车运动学模型，并将航向角偏差、横向偏差和车轮转角误差作为参量设计自动驾驶控制算法。建立的二轮车运动学模型适用于任何前轮转向的车辆，控制算法可以对自动耕作系统所需的各种轨迹进行较为精确的跟踪。由于农田中地况复杂，农机负载多变，因此农机的运动学模型与实际系统会有一定偏差。

为保证控制的鲁棒性，需要更高阶的动力学模型来保证精确的横向控制。文献[10]基于大量实验提出一种农机偏航动力学模型系统，在速度8 m/s的情况下也能保证拖拉机的横向位置精度。文献[14]建立了农机的二轮车动力学模型，应用扩展卡尔曼滤波理论和农机状态方程估计出无法测量的状态参数。总的来说，动力学模型对参数的精确度要求较高，但在实际工程中车辆和田地的参数又很难准确获得。因此为避免建模不准确导致控制效果较差等问题，有学者提出一种几何控制方法——纯追踪控制。文献[16]提出的纯追踪算法，前视距离由BP神经网络确定，并将其应用于农机地边界调头导航。文献[18]针对插秧机自动导航建立模糊控制器，以速度和横向位置偏差作为输入，输出纯追踪算法的前视距离。虽然纯追踪控制能有效避免由模型不准确带来的问题，但对前视距离的计算精度要求较高，否则会引起控制过程中的振荡。PID控制结构简单，适应性强，因此也经常被应用于农机导航控制。但PID控制的主要问题在于针对不同工况时参数整定，以及控制超调和响应时间较为困难。

滑模变结构控制因其对扰动不敏感、调节参数少、响应速度快等优点被广泛应用于非线性控制中。文献[27]针对农用履带机器人提出了一种基于等效控制和切换控制的自适应滑模控制策略，并根据农机运动学模型和电机驱动特性设计了一种变倾斜参数的自适应积分滑模切换函数。该自适应滑模控制方法具有较高的抗干扰性，但控制过程中会有抖振发生。滑模控制的缺点主要是控制的不连续性会引起抖振以及收敛时间无限等。为解决此问题，文献[29]使用自适应滑模控制来提高农机自动转向控制精度，滑模面采用非线性积分的形式。同时通过使用模糊控制方法来自适应调节滑模控制的开关增益以减轻控制输入抖振现象。文献[30]同样在滑模控制中使用模糊控制方法抑制抖振，提高了农机的导航控制精度，但不能保证收敛时间。

针对滑模控制的抖振和收敛时间无限等问题，本文设计一种带非线性干扰观测器的快速终端滑模控制算法，以提高水稻直播机在水田环境下的抗干扰能力和路径跟踪精度。

1 基于干扰补偿的农机运动学模型

由于水田环境下土壤特性复杂，难以建立准确的直播机动力学模型，因此选择建立带滑移和转向干扰补偿的农机运动学模型。如图1所示，不考虑农机动力学特性，将直播机的运动学模型简化为二轮车模型[31]。图中，M(xm,ym)为后轮中心，车体控制点；T(xt,yt)为M点在期望路径T上的垂足;θp为y轴与期望路径的夹角，即航向角的期望值。根据以下5组参数来描述直播机的位姿：直播机后轮中心的大地坐标与期望路径的距离、前轮转角、行驶速度、农机行驶方向与期望路径之间的航向角偏差、前后轮轴距。

由于期望路径AB固定，所以航向角偏差的导数与航向角速度相等，即

(1)

式中V——行进速度，m/s

R——直播机转弯半径，m

θ——航向角，(°)

θe——航向角偏差，(°)

由图中几何关系可得

(2)

式中L——前后轮轴距，m

δ——前轮转角，控制输入，(°)

所以

(3)

横向偏差的导数即为速度V在该方向上的分量，即

(4)

式中de——横向偏差，m

以横向偏差de和航向角偏差θe为状态变量，同时考虑水田中地况复杂多变，为避免未知干扰导致建模不准确和滑模控制器抖振现象发生，特引入农机的滑移和转向干扰。由式(3)、(4)可得带干扰的直播机运动学模型的状态方程为

(5)

式中VR——滑移速度干扰，m/s

δR——前轮转向干扰，(°)

引入复合干扰项：横向位置干扰|ξ|≤P和航向角干扰|ζ|≤K，P和K为干扰的最大值，之后用非线性干扰观测器对其进行精确观测，并补偿到控制器中。复合干扰综合滑移和转向干扰后的直播机运动学模型为

(6)

式中x1——横向偏差，m

x2——航向角偏差，(°)

2 非线性干扰观测器设计

由于在实际工作过程中直播机受到的复合干扰很难直接获得，因此建立非线性干扰观测器对其进行观测。令

(7)

(8)

式中x(t)——状态变量

d(t)——复合干扰

u(t)——控制输入，即前轮转角δ

由式(6)可知，直播机状态方程为

(9)

令复合干扰d的估计为，求得实际值d与估计值的差值，然后对估计值进行补偿得

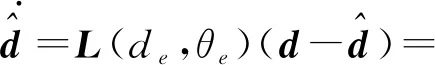
(10)

式中L(de,θe)——正定的增益矩阵

z=-p(de,θe)

(11)

其中

p(de,θe)=L(de,θe)x+D

(12)

式中z——辅助向量

p(de,θe)——设计的函数向量

D——辅助常量矩阵

由式(10)～(12)求得z的导数

(13)

因此，非线性干扰观测器改进后的方程为

(14)

令复合干扰的观测误差ed=d-，由于观测器和复合干扰的动态特性相比，前者变化较为迅速，于是可作出假设所以

(15)

将式(9)、(12)、(14)代入式(15)整理可得

(16)

(17)

因此估计误差ed渐进收敛，选取合适的正定增益矩阵L(de,θe)能让估计误差迅速趋于0，可准确估计出直播机运动学模型中的复合干扰。

3 非奇异快速终端滑模控制器设计

终端滑模[32]的设计思想是在滑模面中引入非线性项，使得系统进入滑模面后能在有限时间内收敛，可解决线性滑模面不适用复杂非线性系统且收敛时间无穷大的问题。传统终端滑模面为

(18)

式中β——非线性项系数，β>0

p、q——正奇数，p>q

系统收敛时间为

(19)

但当系统状态远离滑模面时，以上终端滑模控制收敛速度比较慢。而且由于控制律可能会包含带有负指数的项，当该状态趋于零时会导致控制趋于无穷，即产生奇异现象。为解决以上问题，本文设计能使横向偏差de全局快速收敛的快速终端滑模面

(20)

式中α——线性项系数

将横向偏差de作为重要的路径跟踪精度评价指标。在滑模面的设计中引入de的线性项和非线性幂次项，使得当系统状态远离滑模面时由线性项保证收敛速度，进入滑模面后非线性幂次项起主要作用，从而保证系统具备全局快速收敛的特性。同时控制律中不包含负指数，也不会产生奇异。

趋近律设计为

(21)

式中k、λ——系数，均大于0

由式(6)、(14)、(20)、(21)设计控制律为

(22)

控制律收敛性证明，选取李雅普诺夫函数

(23)

由式(20)、(21)得

(24)

当s>0时

(25)

当s<0时

(26)

4 仿真验证

使用Matlab/Simulink验证本文所提控制算法的有效性。根据图2控制系统结构图建立相应的仿真模型。直播机系统仿真模型参数如表1所示。

表1 控制系统仿真参数Tab.1 Simulation parameters of control system

为了验证本文设计的非线性干扰观测器对复合干扰的估计效果，对控制系统模型施加复合干扰。干扰及其估计曲线如图4、5所示。由图4、5可以看出，观测器对横向位置干扰ξ和航向角干扰ζ的估计值与施加的实际值基本吻合，说明观测器能实现对复合干扰的精确观测，可将观测器的估计值补偿到直播机运动学模型中以提高模型的准确度。

最后验证将观测器估计值补偿到控制器中能否降低干扰造成的抖振。在施加干扰的情况下，仿真对比了3种算法的路径跟踪效果：①带干扰观测的快速终端滑模控制。②不带干扰观测的快速终端滑模控制。③不带干扰观测的传统滑模控制。仿真结果如图6所示。3种算法路径跟踪过程中横向偏差的均方差分别为0.003 3、0.012 6、0.037 7 m。

从图6可知，在有干扰存在但无补偿的情况下，路径跟踪过程中会发生明显的抖振。本文所提的快速终端滑模控制相比传统滑模控制具备一定的抗抖振能力。当有干扰观测补偿时，系统抖振明显降低，说明采用干扰观测器估计干扰值并补偿到控制器中能有效降低滑模控制抖振，提高路径跟踪控制精度，证明了本文所提控制算法的有效性。

5 实验验证

5.1 实验平台

对洋马集团生产的YR10D型水稻直播机进行无人化改造，如图7所示。整车自动驾驶控制系统由上位机主控制器通过CAN/RS-232的通信方式接收北斗位置信息，并对车身各子控制系统进行控制，各子系统相互协作使得直播机完成自主驾驶和作业。主控器采用微嵌Linux工业计算机，具有4核1.6 GHz高性能处理器，以及1 GB DDR3运行内存，支持RS-232串口、CAN等通信接口。采用北京天海科公司生产的DWQT-CAN-360-G型转角传感器，精度为0.1°。RTK-GPS使用4G网络差分基站，动态定位精度在0.02 m以内，数据更新频率为20 Hz。方向盘使用直流电机驱动，采用位置-速度双闭环控制。所使用硬件的精度和频率足以应用于农机自动驾驶中。改造后的直播机能实现自动导航、精量播种、容量检测、堵塞报警、自动倒车加种及自动封边作业。同时建立了云平台管理系统，具备路径规划、远程控制、一机多控及多机协同等功能。实现了“智慧在云，智能在端，管控在屏”的设计理念。

5.2 农机作业实验

为验证本文算法在直播机上的实际运行效果，在上海市崇明区上实集团的水田进行实际带种作业。实验前该地块信息已保存到地块管理系统中，作业前只需加载地块信息，将直播机停在起点处，点击开始，直播机即可自主作业。由于本文所设计的控制算法具备较强的自适应性和鲁棒性，并且对参数不敏感，一般情况无需重新调节参数。因此实验时算法参数与表1中仿真参数保持一致即可取得较好的路径跟踪精度。图8为直播机此次作业的行驶轨迹，可以看出行驶轨迹较为平滑，无偏航。为分析本文所提算法的直线跟踪效果，截取7段直线路径进行分析。设定的作业行距为2.5 m，但由于导航定位存在一定的误差，每段路径相对于理想轨迹都会有一定的横向稳态偏差，路径1～7的稳态误差分别为-0.001 1、0.036 8、-0.033 7、0.033 6、-0.037 4、0.022 0、-0.031 7 m。

消除稳态偏差后，图9显示了每段路径的横向偏差，全过程的航向角变化曲线如图10所示。由图9可以看出，除路径1外，所有路径的横向偏差基本都保持在0.05 m以内。由于路径1是路径跟踪起始阶段，需要一定的适应和调整时间，所以此阶段的横向偏差稍大。由图10可以看出，直线行驶阶段航向角偏差基本为零，每次当直播机行驶到地边界调头时航向角会相差180°，之后收敛到0°，由图中框出部分可以看出，本文所提算法的上线效果优异，收敛速度快，无超调和抖振发生。

各路径横向偏差的概率分布如图11所示，可以看出，消除了稳态误差影响后各路径的横向偏差接近服从以0为均值的正态分布。说明本文所设计的干扰观测器对复合干扰进行观测补偿后，有效抑制了直播机在水田环境下的抖振，使得直线跟踪阶段横向偏差在0附近波动幅度较小。各路径跟踪过程中横向偏差和航向角偏差的统计特性如表2所示。横向偏差总体最大值为0.089 5 m，最小值为-0.128 3 m，平均绝对偏差为0.024 7 m，均方差为0.031 1 m。最值都出现在路径1中，由于是初始阶段，所以路径1各项数据都较其他稍大，路径5各项数据最小。航向角偏差总体最大值为4.249 6°，最小值为-5.631 8°，平均绝对偏差为0.923 6°，均方差为1.189 3°，同样表明本文所提算法具有较优异的路径跟踪效果。并且航向角偏差具有和横向偏差同样的性质，体现了数据的一致性。

各项实验数据显示，本文所设计的控制算法在转弯和直线跟踪过程具有快速收敛的特性。通过对复合干扰进行精确观测并补偿到控制器中能有效抑制干扰造成的抖振。本文算法具有优异的路径跟踪效果，能较好地满足实际播种作业的要求。

6 结论

(1)建立基于干扰补偿的水稻直播机运动学模型，提出了一种基于非线性干扰观测器的快速终端滑模控制算法。使用Matlab/Simulink进行了系统仿真，结果表明，本文提出的快速终端滑模控制算法在初始横向偏差为-0.6 m时，调节时间约为2.5 s，相比于终端滑模和传统滑模具有全局快速收敛的特点，且无超调。

(2)在水稻直播机的运动学模型中加入横向位置干扰和航向角干扰，并设计非线性干扰观测器对其进行估计。结果显示，系统的不确定性干扰能被建立的非线性干扰观测器精确地观测出，补偿到滑模控制器后能有效抑制干扰造成的抖振。

表2 各路径横向偏差和航向角偏差统计结果Tab.2 Statistical characteristics of lateral deviation and heading angle deviation of all driving paths

(3)以速度1.2 m/s进行了水田播种作业实验，直线跟踪过程中横向平均绝对偏差为0.024 7 m，均方差为0.031 1 m，航向角平均绝对偏差为0.923 6°，均方差为1.189 3°。偏差总体数值较小，分布集中，并且转弯时收敛速度较快，无超调。本文所提出的快速终端滑模控制算法收敛时间快，所设计的非线性干扰观测器能有效抑制水田环境下不确定性复合干扰对路径跟踪造成的抖振。