大倾角底坡泄槽收缩段水流水力特性模型试验研究
2021-02-14张小飞覃培何飞龙黄佳敏肖天培吴健
张小飞,覃培,何飞龙,黄佳敏,肖天培,吴健
(广西大学 土木建筑工程学院, 广西 南宁 530004)
0 引言
由于受地形、地质因素的影响或出于消能防冲等原因,泄水建筑物往往会设有收缩段。收缩段的主要缺点是水流受收缩边墙的影响会产生水流冲击波,从而引起泄水建筑物过水断面的流量分布不均,影响收缩段及其下游的流态。目前,国外学者对边墙收缩式泄槽的水流特性已做了诸多有益的研究,IPPEN[1]以力学原理为基础,系统地阐释了水工泄槽收缩段的水流冲击波的一般特性,并假定:①冲击波前后的压强都遵循静水压强分布规律;②冲击波上、下游的流速均服从均匀分布;③冲击波波头处的厚度为零;④泄槽底坡为平底。在这四个基本假定下提出了冲击波理论。JAN等[2]进行了泄槽收缩段的水流冲击波特性实验,得出了冲击角、最大冲击波高度和最大冲击波对应位置的三个经验无量纲关系,并且对IPPEN冲击波基本假定进行深入探讨,深化和扩展了急流冲击波理论的研究深度和适用范围。HAGER[3]提出了改进的关于强冲击波的近似计算式,并且相较于IPPEN提出的冲击波关系式其精度更高。
国内许多研究工作者[4-9]应用、改进和发展了急流冲击波理论,并将其应用于溢洪道泄槽的水力设计中,也给出了泄槽冲击波的数值计算方法和计算简化式。刘韩生等[10]以IPPEN提出的冲击波理论为基础,推导出新的冲击波简化式,解决了IPPEN所提冲击波理论式计算时需要进行试算的问题,提高了计算效率。韩守都等[11]应用辐射水流特性计算窄缝挑坎中线水面线,提出一级直线窄缝挑坎水力计算方法,可比较简单地计算水面线和水舌挑距。吴永妍等[12-13]通过模型试验研究,总结出了不同长度收缩段内纵向时均流速及紊动强度的分布规律。刘亚坤等[14]、黄智敏等[15]结合模型试验分析,认为IPPEN冲击波理论对于泄槽边墙转角较小、来流的佛氏数较低、收缩段沿过水断面的宽度远大于其水深的情况,其计算结果才与实际较吻合,而大底坡、大收缩角收缩段内的波阵面前后的水力学要素、冲击波的传播都和IPPEN冲击波理论假设有较大差异,波阵面后的压强不符合静水压强分布,水深、佛劳德数Fr和波角沿程是变化的,采用IPPEN冲击波理论来分析计算大倾角、大收缩角收缩段的水力学问题不合理。为此,刘亚坤等[14]通过模型试验研究了底坡对急流冲击波的影响,提出了计算急流冲击波的角度和深度之比的一种近似方法,并在垂直冲击波波阵面方向的动量方程中引入一个动水压强修正系数来体现坡底的影响,认为由于底坡的影响,弗劳德数沿着激震前沿来流逐渐增大,因此在每一部分都提出了确定弗劳德数的方法,但在建立冲击波法向和切向动量方程时没有考虑自重的影响。黄智敏等[15-16]依据窄缝挑坎收缩段的试验结果对溢洪道陡坡收缩段边墙水深计算方法进行了研究,考虑了陡坡段边墙转角、坡度和激震水跃段水体重量等因素,但还是采用了波阵面后的压强符合静水压强分布的假定。
综上所述,这些研究对IPPEN冲击波理论在顺坡收缩泄槽冲击波计算时进行了修正,扩大了IPPEN冲击波理论的适用范围,但这些修正是根据特定试验进行的,而且在相关公式的推导中,也不同程度地采用了IPPEN的假定或引入一些新的假定,修正后的计算公式的适用性还有待进一步验证。基于此,本文结合重力坝的建设需要,采用水工模型试验对大底坡(50°~60°)大收缩角(20°~30°)泄槽直线边墙收缩段水力特性开展研究,进一步揭示大底坡、大边墙收缩角泄槽收缩段内的水力特性,并为大底坡、大边墙收缩角泄槽收缩段内水流计算及研究提供参考。为了避免和水力学中的缓流、急流对应的缓坡和陡坡发生混淆,并方便表述,本文将倾角大于45°的底坡称为大倾角底坡,同时把收缩角大于15°的收缩段称为大收缩角收缩段。
1 试验设计
1.1 模型设计
为了能更直观地探究大倾角底坡和大边墙收缩角变化对泄槽直线边墙收缩段的水深、边墙处水压力及冲击波波角的影响,采用水工模型试验作为研究方法。为了使研究成果能适用于大倾角底坡溢洪道和溢流坝,试验的底坡的取值范围取中、高溢流坝下游直线段坡度的常见取值范围1∶0.6~1∶0.8,对应的倾角为51.34°~59.04°。目前边墙收缩角小于15°的收缩段已有不少的研究,而收缩角大于15°的收缩段的研究成果还不多见,为此结合实际工程可能出现的收缩角,选取20°~30°作为试验收缩角的取值范围。根据试验场地的环境和条件,收缩段进口宽度为100 cm,出口宽度为30 cm,为了保证各试验工况时收缩段起始断面处的水流流态相似,均为均匀流,保证各试验结果的可比性,在收缩段前设置了底坡和收缩段一致、长度为30 cm的调整段。泄槽模型使用有机玻璃制作,泄槽模型示意图如图1所示。模型为对称模型,在左边墙上沿水流方向布置了两个时均动水压力测量断面,每个测量断面上设置5个测点,不同收缩角时测点布置如图2所示。试验通过阀门进行流量控制;采用LGY-Ⅲ型多功能智能流速仪和声学多普勒流速仪ADV进行流速测量,试验采用φ15(旋浆直径为15 mm)的流速旋浆传感器,采样时间为30 s;边墙水面线根据边墙上的刻度尺直接读取,中线水面线使用水位测针量测;使用测压管获取时均动水压力;使用刻度尺测量波阵面起始断面与下游断面的水深。每组次重复测量3次,以其平均值作为最终结果。

(a) 泄槽模型俯视图
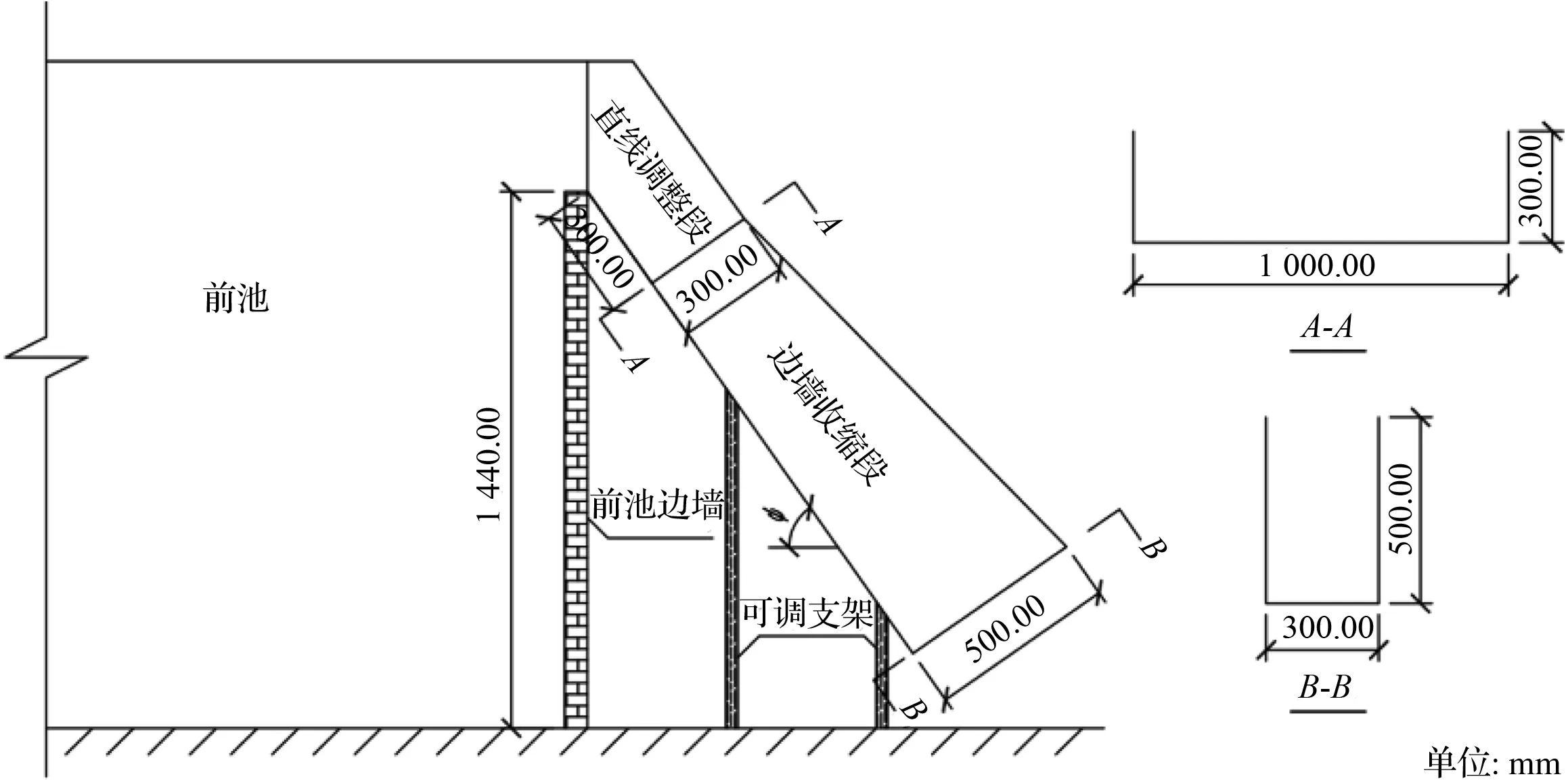
(b) 泄槽模型侧视图

(a) α=30°边墙测点布置

(b) α=25°边墙测点布置

(c) α=20°边墙测点布置
1.2 模型参数
根据正交性原则,从泄槽收缩段的底坡倾角与边墙收缩角两个方面对试验进行设计,各组试验方案模型参数见表1。根据试验模型尺寸和系统供水能力,每组试验分别测试5个试验流量,限于篇幅,本文只列举了3.02×10-2、3.89×10-2、5.13×10-2m3/s三个流量的试验成果。

表1 试验方案模型参数Tab.1 Model parameters of test scheme
2 试验结果与分析
分析底坡倾角对边墙收缩段水力特性的影响时,选取边墙收缩角为25°,底坡倾角分别为51.34°、55.01°和59.04°组次的试验结果。分析边墙收缩角对边墙收缩段水力特性的影响时,则选取底坡倾角为55.01°,边墙收缩角分别为20°、25°和30°组次的试验结果。
2.1 底坡倾角与边墙收缩角对收缩段水深的影响
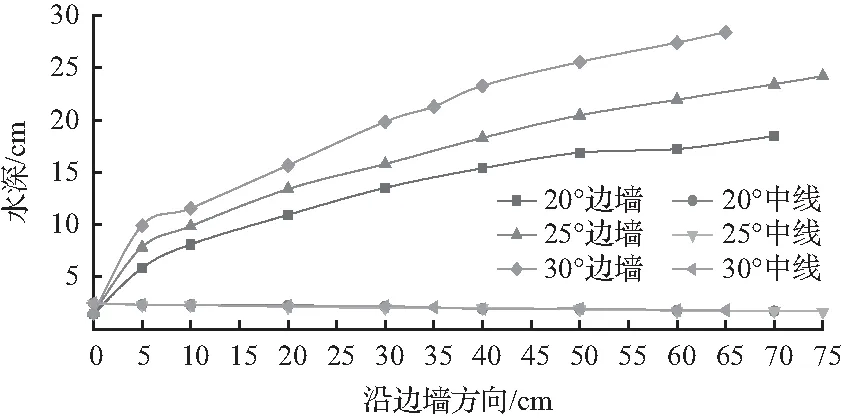
图3(a)至图3(c)是边墙收缩角为25°时不同倾角底坡的收缩段水深变化图,图3(d)至图3(f)是边墙收缩角为55.01°时不同边墙收缩角的收缩段水深变化图。
试验观测发现,和小倾角收缩段水流产生的冲击波相比,由于泄槽底坡倾角大,水流流速更高,冲击波的传播速度和水流的速度之比变小,边墙收缩产生的冲击波的影响范围很小,只有紧邻边墙的水流受冲击波的影响,如图4(a)所示,图4(a)中左右两侧线框区域代表冲击波的影响范围。在相同流量下,中线水深沿程有所减小但是幅度不大,水面线均基本呈直线,说明中线处水深不受收缩边墙的影响,这和基于窄缝收缩水流的文献[15]、[16]的表述不同,用文献[16]的公式计算过水断面宽度远大于水深的收缩段波阵面上游的水深并不合理。在边墙处,水流与收缩边墙交汇时产生跃起,边墙处水面线明显的跃升,跃起的水流沿边墙向下流动,靠近边墙、先与收缩边墙交汇跃起的水流位于表面,离边墙较远、后与收缩边墙交汇跃起的水流位于底部,水流分层明显,如图4(b)和图4(c)所示,图4(b)和图4(c)中深色水体为在收缩段起点处投放示踪剂的示踪水体。

(a) α=25° Q=3.02×10-2 m3/s

(b) α=25° Q=3.89×10-2 m3/s

(c) α=25° Q=5.13×10-2 m3/s

(d) ψ= 55.01° Q=3.02×10-2 m3/s

(e) ψ= 55.01° Q=3.89×10-2 m3/s
(f) ψ= 55.01° Q=5.13×10-2 m3/s

(a) 泄槽整体水流流态
边墙处水面线主要由收缩起点处跃起的水流决定,收缩角对边墙处的水深影响较大;从图4中可以看出,沿边墙流动的水流与IPPEN基本假定不相符,采用IPPEN提出的冲击波计算公式计算大底坡直线边墙收缩段沿边墙流动水流的水深显然不合适,文献[16]虽然考虑了陡坡段坡角的影响对IPPEN公式进行改进,但还是采用了波阵面后的动水压强符合静水压强分布的假定,其提出的波阵面下游区沿程水深计算公式的合理性还值得进一步验证。
2.2 收缩段边墙处的时均动水压力
图5至图8是不同底坡倾角和不同收缩角时边墙处时均动水压力分布图。从图5至图8中可以看出,大倾角底坡、大边墙收缩角泄槽收缩段内边墙时均动水压力与边墙水深的关系远非线性。
初步分析,出现时均动水压力非线性分布的原因是:边墙处下部水流由于冲击水流的挤压,其动水压力大于静水压力,而上部的水流为上游产生而沿边墙向下流动的水流,在自重作用下,有向下运动、脱离边墙的趋势,测点与水面的距离不是水力学意义上的水深,水流对边墙产生的压力受流速和水流厚度的影响,水压力与水面的距离的关系具有明显的非线性。不同边墙收缩角、不同断面的均动水压力沿边墙水深的变化规律明显不同。希望通过引入用单一动水压力分布修正系数对波后水压力分布进行修正,然后利用IPPEN提出的冲击波计算公式来求解大倾角底坡大收缩角泄槽直线边墙收缩段产生的冲击波问题是否可行还需要进一步研究。

(a) Q=3.02×10-2 m3/s

(a) Q=3.02×10-2 m3/s

(a) Q=3.02×10-2 m3/s

(a) Q=3.02×10-2 m3/s
2.3 收缩段水流冲击波波角
波角是冲击波的扰动线与来流的夹角,反映了冲击波的强弱及影响范围。波角与泄槽两侧边墙引起的冲击波的交汇点位置有直接关系,是重要的设计参数。为探讨现行冲击波理论对大倾角条件下冲击波计算适用性,将波角的试验值和理论计算结果进行对比分析。对于波角的试验值,测量出收缩边墙末端干扰区宽度和边墙长度,根据它们之间的三角函数关系即可得到波角的试验值;对于波角的理论计算值,将试验测得的波前水深和流速代入广泛应用的IPPEN冲击波理论式[1][见公式(1)、(2)]。


式中,β为冲击波波角;α为边墙偏转角;Fr为收缩段起始断面的弗劳德数;h1、h2分别为起始断面与波阵面下游断面水深。
采用试算法即可求得冲击波波角,第一断面波角计算值与试验值的比较见表2。
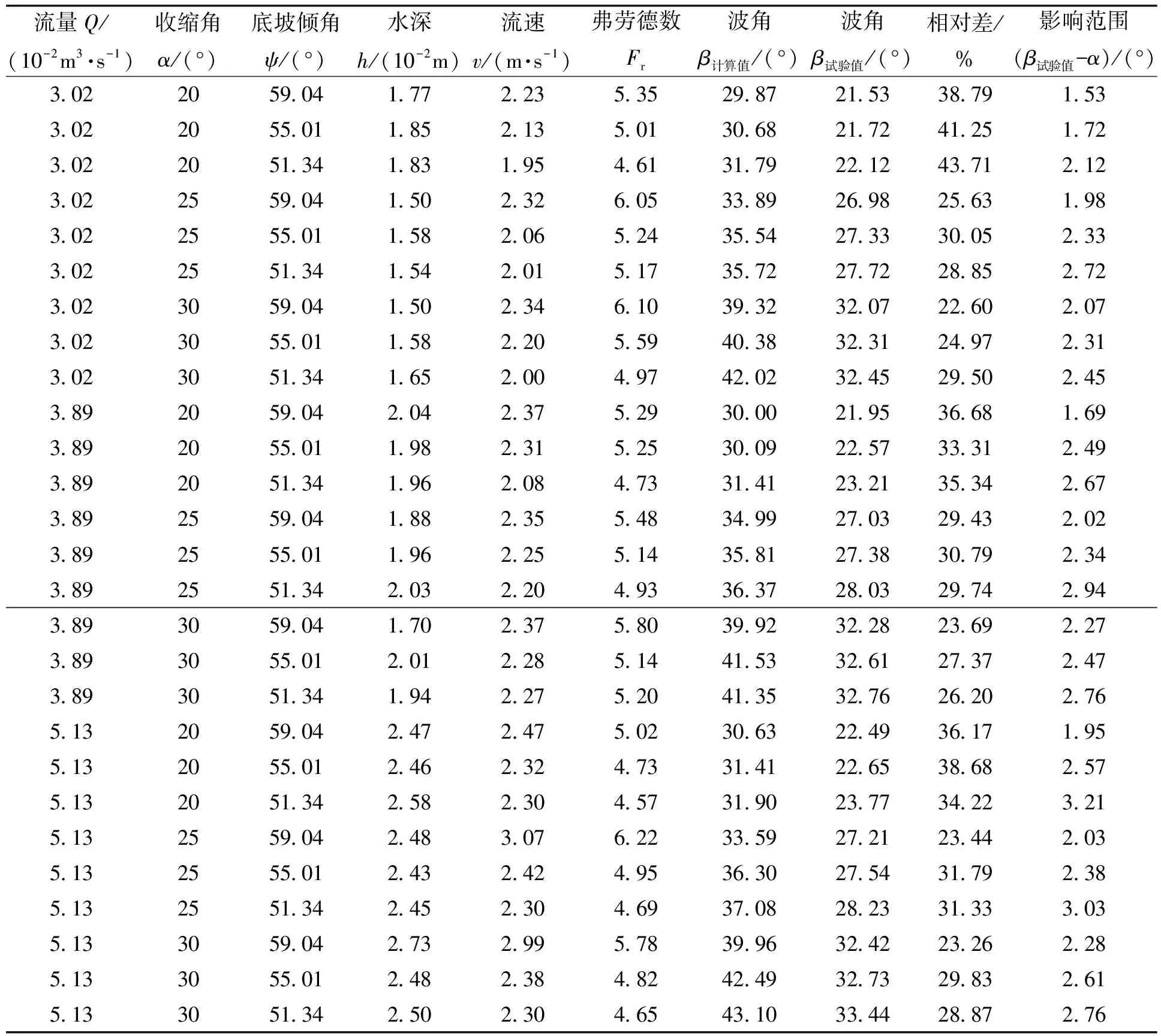
表2 第一断面波角计算值与试验值的比较Tab.2 Comparison between calculated and experimental wave angles
将波角的试验值和理论计算值进行对比发现,在大倾角泄槽条件下,直线边墙收缩段中的冲击波波角小于理论计算值;来流流量相等时,在相同边墙收缩角条件下,泄槽倾角越大,收缩段入口断面流速越大,弗劳德数Fr越大,冲击波波角β试验值和理论计算值越小,即冲击波影响范围(β试验值-α)随着弗劳德数的增大而减小;而当来流流量相等时,在相同底坡倾角条件下,冲击波影响范围并没有随着边墙收缩角的改变而发生明显变化,认为边墙收缩角对冲击波影响范围影响不大;在所有试验方案中,波角相对差最小为22.60%,最大相对差为43.71%。初步分析是因为大倾角泄槽中的水流在平行于坡面的方向上具有较大的流速,水流与边墙冲击产生的冲击波的横向传播速度远小于水流流速,所以冲击波波角较小。由于大倾角泄槽与小倾角泄槽之间的水力特性存在较大差异,所以大倾角泄槽直线边墙收缩段的水力特性值得进行深入研究。
3 结论
① 大倾角底坡泄槽水流流速高,边墙收缩产生的冲击波的波角很小,只有紧邻边墙的水流受冲击波的影响;在大收缩角边墙处,水流与收缩边墙交汇时产生跃起,边墙处水面线明显的跃升,先后跃起的水流沿边墙向下流动,水流分层明显,边墙处水面线主要由收缩起点处跃起的水流决定,收缩角对边墙处的水深影响较大。
② 边墙处水深(测点与水面的距离)不是水力学意义上的水深,时均动水压力与边墙水深的关系远非线性,不同边墙收缩角、不同断面的时均动水压力沿边墙水深的变化规律明显不同,希望通过引入单一动水压力分布修正系数对波后水压力分布进行修正,然后利用IPPEN提出的冲击波计算公式来求解大底坡大收缩角泄槽边墙收缩产生的冲击波问题是否可行还需要进一步研究。
③ 在大底坡倾角、大收缩角的条件下,收缩段断面缩窄范围更大,引起泄流断面单宽流量变化更加剧烈且流速更快,这与IPPEN公式的基本假设条件差异大,所以大底坡倾角泄槽直线边墙收缩段所产生的急流冲击波的形态与小倾角水流冲击波差异较大,现有冲击波理论计算得到的波角比试验值大,波角相对差约在20%~40%。根据本论文的试验观测和其他同类研究的成果,建议IPPEN公式应用于底坡倾角大于30°、收缩角大于15°的过水建筑物水流计算分析时,同时采用模型试验等方法进行验证。
