同步链与纯正非同步半群

李旺威, 黎先华

(1. 岭南师范学院数学与统计学院, 广东 湛江 524048; 2. 苏州大学数学科学学院, 江苏 苏州 215006)

Cerny猜想是同步自动机研究的重要问题之一,许多科学技术问题可以用同步自动机模型来解决[2-5]．近年来, 国际上一些著名的群论及半群的专家投入到该问题的研究, 获得了许多创新的成果．2014年, Araújo等[6]证明了本原群同步于每一秩为n-2的变换, 本原群同步于每一秩为2的变换和本原群同步于每一秩为3或4的非一致变换．2019年, Ryzhikov[7]给出无非平凡圈自动机同步字长度的上下界．近年来, Li等[8-9]解决了几乎同步群的两个公开问题, 并证明了非本原群同步于一类非一致变换．本文拟讨论置换群和一个非可逆变换是否可以生成一个常量映射．

1 判断同步半群的方法

若半群〈G,α〉包含一个常量映射, 则称G同步于变换α．若半群的每一个元素都落在一个子群中, 则称该半群是完全正则的．设α∈TnSn和ker(α)={A1,A2,…,Ar}, 则定义α的核类型为[|A1|,|A2|,…,|Ar|]．若半群〈G,α〉是非同步半群, 则存在β∈〈G,α〉G使得半群〈G,β〉完全正则．因此, 完全正则半群在非同步半群中扮演着“堤坝”的角色, 即完全正则半群能阻止生成集生成常量映射, 自然希望能找到一些特殊的元素“打破”这个“堤坝”,首先给出同步链的定义．

设S是Tn的子半群和e∈S．若e2=e,则称e是S的幂等元, 且记E(S)={x∈S:x2=x}．设Y={a1,a2,…,at}是集合Xn的子集,e是Tn的幂等元, 且满足aie=a(ai,a=at∈Y)和xe=x(x∈XnY), 记为e=[a1,a2,…,at], 其中at=a．

设ei=[ai1,ai2,…,ait](i=1,2,…,r)．对于幂等元ei, 若非单点核类是一个同步链,则称集合E={e1,e2,…,er}具有性质SYN．由于e1e2…er是一个常量映射, 则半群S是同步的．因此, 若E(S)包含一个具有性质SYN的子集E,则该半群S是同步的．根据上面的方法,可给出一些满足Cerny猜想的变换半群．

例2根据上面的符号,有

1) 设Tn=〈Sn,[1,2]〉．由于α=[1,2][2,3]…[n-1,n]是常量映射,且

(1,3)[1,2](1,3)=[3,2],(3,2)[3,2](3,2)=[2,3],

(2,4)[2,3](2,4)=[4,3],(4,3)[4,3](4,3)=[4,3],

…

(n-2,n)[n-1,n-2](n-2,2)=[n,n-1],(n,n-1)[n,n-1](n,n-1)=[n-1,n],

其中(i,j)∈Sn, 则α*=[1,2]g1[1,2]g2…gn-2[1,2]gn-1是一个常量映射．换言之, 在集合E(Tn)中存在具有性质SYN的子集E={[1,2],[2,3],…,[n-1,n]},故Tn是同步半群,且α*的长度为2(n-1); 因此,全变换半群Tn=〈Sn,[1,2]〉满足Cerny猜想．

2) 对于α∈Tn, 定义Z(α)=XnXnα, 且记|Z(α)|为α的亏数．设Singn=TnSn．由于Singn的任一元素是亏值1的幂等元的乘积,有Singn=〈e∈E(Singn):Z(e)=1〉．又由于[i,i+1]∈{E(Singn):Z(e)=1}, 其中1≤i≤n-1, 则在集合E(Singn)中存在具有性质SYN的子集E={[1,2],[2,3],…,[n-1,n]}, 故α*=[1,2]g1[1,2]g2…gn-2[1,2]gn-1是一个常量映射且α*的长度为(n-1); 因此,半群Singn=〈e∈E(Singn):Z(e)=1〉满足Cerny猜想．

3) 设K(n,r)={α∈Singn: rank(α)≤r}．Evseev等[10]已证明K(n,r)由秩为r的幂等元生成, 即K(n,r)=〈e∈E(K(n,r)): rank(e)=r〉．由于[i,i+1,…,i+t]∈{E(K(n,r)): rank(e)=r}, 其中i=1,1+t,1+2t,…; 1≤t≤n-1, 则在集合E(K(n,r))中存在具有性质SYN的子集E, 故α*=[1,2,…,1+t][1+t,3+t,…,1+2t]…[1+rt,2+rt,…,n]是一个常量映射且α*的长度为(n-1); 因此, 半群〈e∈E(K(n,r)): rank(e)=r〉满足Cerny猜想．

4) 设On是Singn的子半群, 且由Xn上的保序变换组成．Howie[11]证明了On由亏值1的幂等元生成, 即On=〈e∈E(On):Z(e)=1〉．由于[i,i+1]∈{e∈E(On):Z(e)=1}, 其中1≤i≤n-1, 则在集合E(On)中存在具有性质SYN的子集E, 故α*=[1,2][2,3]…[n-1,n]是常量映射且α*的长度为(n-1); 因此, 半群〈e∈E(On):Z(e)=1〉满足Cerny猜想．

6) 设G是Xn上的循环群, 其中n是素数,设幂等元e=[1,2]．由于

…

对于本原群G,应用同步链的概念可以证明下面两个类型变换半群是同步的．

引理3设G是集合Xn上的本原群,A⊆Xn,则存在Xn的一个同步链,即存在gi∈G(i=1,2,…,r)使得[A,Ag1,…,Agr]是Xn的一个同步链．

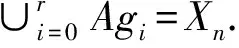
定理4设G是集合Xn上的本原群,e是核类型为(t,1,…,1)(t≥2)的幂等元, 则S=〈G,e〉是同步半群和常量映射的长度至多为2(n-1)．

注: 对于一般的变换α,较难确定半群〈G,α〉是否同步．然而,基于定理4,可以通过判断群G和α是否可以生成核类型为(t,1,…,1)(t≥2)的变换,从而确定半群〈G,α〉是否同步．利用代数软件GAP可以发现本原群G与很多类型的变换α能生成核类型为(t,1,…,1)(t≥2)的变换．

定理5设G是集合Xn上的本原群,e是核类型为(2,2,1,…,1)的幂等元, 则S=〈G,e〉是同步半群．

证明 设e是核类型为(2,2,1,…,1)的幂等元,A1和A2是e的非单点核类．由G的本原性知,存在g1,g2,g3∈G使得A1e1={a1},A2e1={a2}与{a1,a2}⊆B, 其中e1=(eg1)r1和e2=(g2eg3)r2是幂等元,B是ker(e2)的核块; 因此,A1∪A2是ker(e1e2)的块,从而f=e1e2是核类型(4,1,…,1)的幂等元．由定理4, 得〈G,f〉是同步半群,故S=〈G,e〉是同步半群．

2 纯正非同步半群

对于半群S和S中元素a, 若存在x∈S使得axa=a,则称a是S的正则元．若半群S的每个元素都是正则的,则称S是正则半群．若半群S是正则的且其幂等元集合是一个子半群,则称为纯正半群．半群S的Green关系L,R,H,D,J分别定义为: 对于a,b∈S,aLb⟺S1a=S1b,aRb⟺aS1=bS1,H=L∩R,D=L∘R=R∘L,aJb⟺S1aS1=S1bS1．McAlister[13]证明了半群S=〈G,e〉是纯正半群．

定理6[13]设G是Xn上的置换群和e=[1,2]是幂等元．若2属于1所在的轨道上, 则半群S=〈G,e〉是纯正的当且仅当存在g∈G使得1g=2,g2∈F和g-1Fg=F,其中F是G上关于1的稳定子群．

对于上面的结论,可以发现半群S=〈G,e〉是非同步的．证明该结论, 须先证明〈G,α〉是完全正则的,即下面的引理．设G是Xn上的传递非本原群,Δ是G的非平凡块,Σ={Δg:g∈G}是G的完全非本原系．

引理7设G是Sn的子群和α∈TnSn且满足rank(α2)=rank(α), 则S=〈G,α〉是完全正则半群当且仅当对任意的g∈G有rank(αgα)=rank(α)．

证明 设S=〈G,α〉是完全正则半群．由于〈G,α〉G是完全单的,即仅有一个J-类, 则对于任意的g∈G,α和αg都属于这个J-类, 故对任意的g∈G有rank(αgα)=rank(α)．

反之, 设对任意的g∈G有rank(αgα)=rank(α)．由于α且满足rank(α2)=rank(α), 则存在幂等元e使得(α,e)∈H, 即e和α满足im(e)=im(α), ker(e)=ker(α)．注意到, 对任意的g∈G有rank(αgα)=rank(α)等价于对于任意的g∈G有g映射im(α)成ker(α)的一个横截, 故对于任意的g∈G有g映射im(e)成ker(e)的一个横截,则对任意的g∈G有rank(ege)=rank(e), 从而〈G,e〉是完全正则半群．

设x=αg1αg2…αgth∈〈G,α〉, 其中g1,g2,…,gt,h∈G．由(α,e)∈H,有(αgi,egi)∈H．又因〈G,e〉是完全正则半群,〈G,e〉G和〈G,α〉G有相同的幂等元集合,故存在幂等元f∈〈G,e〉使得(αg1αg2…αgt,f)∈H,则对于任意的g∈G有g映射im(f)成ker(f)的一个横截．因为x与αg1αg2…αgt相差一个群元素h,所以存在幂等元f′∈〈G,e〉使得(x,f′)∈H．由于有限群的子半群是一个子群, 则〈G,α〉∩Hf′是一个以f′为单位元的群．由此可知,〈G,α〉的任一元素都属于某个子群,故〈G,α〉是完全正则半群．

定理8对定理6中的群G和幂等元e, 半群S=〈G,e〉是非同步半群．

证明 对于定理6中的G和幂等元e,G一定是非传递的或传递非本原的．设G是非传递群．由于G有k(k>1)条轨道且集合{1,2}包含在1条轨道中,则半群S=〈G,e〉中元素的最小秩为k,即S中没有常量映射,故S是非同步半群．

设G是传递群．由于G满足定理6的条件,则{1,2}⊆Δ, 其中Δ是G的非平凡块．若{1,2}=Δ, 则对任意的g∈G,{1,2}都不能吸收其他单点成为一个新的核类．但对于g∈G, 变换ege的非单点核类由单点构成,且该非单点核类是一个非平凡块, 故存在hi∈G,i=1,2,…,s, 使得ker(eh1eh2…hse)={Δg:∈G}．若{1,2}⊂Δ, 存在h∈G使得Bj∈ker(ehe)和Ai⊂Bj⊆Δg, 故存在hi∈G,i=1,2,…,s,使得{1,2}吸收单点变成一个非平凡块, 且e的单点也合并成G的非平凡块, 有ker(eh1eh2…hse)={Δg:g∈G}．令β=eh1eh2…hse,则对所有g∈G, 有rank(βgβ)=rank(β)．根据引理7, 〈G,β〉是完全正则半群, 得rank(β)是半群S中元素最小的秩, 故半群S是非同步半群．

利用代数软件GAP[14]尝试确定满足定理8中的群类, 称该类群为纯正非同步群,结果如表1所示．图1为GAP程序．通过GAP软件可以确定其生成集, 但在GAP软件中至多能计算级数为30的传递置换群,而级数为16的传递置换群有1 954个, 且绝大部分级数为16的传递群都满足定理8的条件,故表1中仅给出级数为16传递群的一些代表元．同样地,级数为18,20,24,28,30的传递置换群的个数分别是983,1 117,25 000,1 854,5 712,表1也仅列出部分代表元．表1中符号的含义为:E(4)表示级数为4的第2个传递置换群;D6(6)表示级数为6的第2个传递置换群;E(8),E(8):2,E(8):E4分别表示级数为8的第3,9,18个传递置换群;D(10) 表示级数为10的第2个传递置换群;D6(6)[×]2表示级数为12的第3个传递置换群;D14(14)表示级数为14的第2个传递置换群; TnNi表示级数为n的第i个传递置换群．

图1 GAP程序

表1 纯正非同步群