化学平衡态的存在性、唯一性与稳定性问题
2021-02-12周鲁
周鲁
四川大学化工学院,成都 610065
化学平衡是物理化学课程的重要教学内容。实际上,化学平衡也是所有化学类课程的重要教学内容。然而,对于一个给定的化学反应是否存在化学平衡态?如果存在化学平衡态,有几个化学平衡态?如果存在化学平衡态,这些化学平衡态是否稳定?以上即为关于化学平衡态的存在性、唯一性与稳定性问题。对于这些具有重要的理论意义和实际意义的问题,迄今为止的国内外物理化学教材[1-4]都没有给出过明确的回答。有鉴于此,本文将对这些问题进行讨论,以供同行在化学平衡教学中参考。
1 化学平衡态问题的数学背景
设在封闭系统内发生了一个化学反应,则反应系统的吉布斯函数G是温度T、压力p和反应进度ξ的函数,即:

在等温等压条件下,根据偏摩尔量集合公式,反应系统的吉布斯函数G仅仅是反应进度ξ的函数:

式中nB是反应系统中组分B的摩尔数,μB是组分B的化学势,它们都是反应进度ξ的函数。在等温等压条件下,反应系统的吉布斯函数G随反应进度ξ的变化率为:

式中vB是化学反应方程式中组分B的计量系数,ΔrGm是摩尔反应吉布斯函数,它是反应进度ξ的函数。在等温等压条件下,反应系统的摩尔反应吉布斯函数ΔrGm随反应进度ξ的变化率为:

从数学上看,式(2)、(3)、(4)分别给出了在等温等压条件下,反应系统的吉布斯函数G(ξ)及其一阶导数和二阶导数的表达式。按照定义,反应进度ξ的取值范围是闭区间[0, 1],而吉布斯函数G(ξ)及其一阶导数和二阶导数都是闭区间[0, 1]上的连续函数。从数学上看,化学平衡态的存在性问题,就是要判断吉布斯函数G(ξ)在开区间(0, 1)内是否存在极值?化学平衡态的唯一性问题,就是要判断吉布斯函数G(ξ)在开区间(0, 1)内是否仅存在唯一极值?而化学平衡态的稳定性问题,就是要判断吉布斯函数G(ξ)在开区间(0, 1)内是否存在极小值?下面分别讨论之。
2 化学平衡态的存在性

如果ΔrGm(0) < 0和 ΔrGm(1)> 0 成立,则有 ΔrGm(0)· ΔrGm(1) <0 成立。根据零点定理,一定存在ξe∈ (0,1),使得 ΔrGm(ξe) = 0成立。即在等温等压条件下,可以自发进行但又不能进行到底的理想气体或理想溶液反应系统一定存在化学平衡态。
3 化学平衡态的唯一性
如上所述,化学平衡态的唯一性问题,就是要判断函数G(ξ)在开区间(0, 1)内是否存在唯一极值?为了判断化学平衡态的唯一性问题,引入下述的单调定理[5,6]:
如果函数f(x)是闭区间[a,b]上的连续函数和单调函数,并且f(a)·f(b) <0 成立,那么在开区间(a,b)内仅仅存在唯一的c∈ (a,b),使得函数f(c)=0。
从数学上看,因为ΔrGm(ξ)是闭区间[0, 1]上的连续函数,如果ΔrGm(0)·ΔrGm(1) < 0成立,根据零点定理,吉布斯函数G(ξ)在开区间(0, 1)内一定存在极值。如果ΔrGm(ξ)同时还是闭区间[0, 1]上的单调函数,按照单调函数的定义,当ξ2>ξ1时,必定有 ΔrGm(ξ2)> ΔrGm(ξ1)或者 ΔrGm(ξ2)< ΔrGm(ξ1)成立。那么ΔrGm(ξ)从ΔrGm(0)< 0 连续变化到 ΔrGm(1) > 0 的过程,只能有一次经过 ΔrGm(ξe) = 0的状态。也就是说,仅仅存在一个ξe∈ (0,1),使得 ΔrGm(ξe) = 0成立,即吉布斯函数G(ξ)在开区间(0, 1)内仅仅存在唯一极值。
例如,对于理想气体或理想溶液反应系统,如前所述,当 ΔrGm(0)<0和 ΔrGm(1)> 0 成立时,根据零点定理,反应系统存在化学平衡态 ΔrGm(ξe) =0。根据式(7),有:
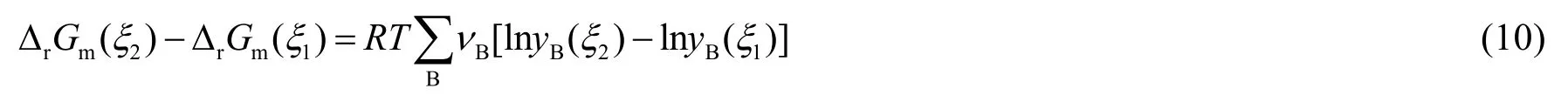
因为在从 ΔrGm(0) <0 连续变化到 ΔrGm(1) >0 的过程中,产物的摩尔分数随反应进度的增大而增大,反应物的摩尔分数随反应进度的增大而减小,即当ξ2>ξ1时,若νB>0,则 lnyB(ξ2)>lnyB(ξ1),若νB<0,则 lnyB(ξ2)<l nyB(ξ1)。所以对于理想气体或理想溶液反应系统,当ξ2>ξ1时有:

即ΔrGm(ξ)是闭区间[0, 1]上的单调递增函数。根据单调定理,则仅仅存在一个ξe∈ (0,1),使得ΔrGm(ξe) = 0成立。即在等温等压条件下,可以自发进行但又不能进行到底的理想气体或理想溶液反应系统仅仅只有一个化学平衡态。
4 化学平衡态的稳定性
如上所述,化学平衡态的稳定性问题,就是要判断函数G(ξ)在开区间(0, 1)内是否存在极小值?为了判断化学平衡态的稳定性问题,引入下述的极值定理[5,6]:
如果函数f(x)是闭区间[a,b]上的连续函数,并且存在c∈ (a,b)使得f′(c)=0。那么当f′′(c)<0时,f(c)为极大值;当f′′(c)>0时,f(c)为极小值。
从数学上看,因为ΔrGm(ξ)是闭区间[0, 1]上的连续函数,如果ΔrGm(0)· ΔrGm(1) < 0成立,根据零点定理,一定存在ξe∈ (0,1),使得 ΔrGm(ξe)=0成立。如果当ξ=ξe时,成立,那么G(ξ)e不仅是吉布斯函数G(ξ)在开区间(0, 1)内的极值,而且是极小值。
从物理上看,吉布斯函数G(ξ)的增量只与始末态有关而与过程无关,这就表明吉布斯函数G(ξ)具备势函数的特征。因此吉布斯函数G(ξ)的极小值G(ξe)就是势函数的极小值,而势函数的极小值在物理上代表系统处于稳定状态。
例如,对于理想气体或理想溶液反应系统,如前所述,当ΔrGm(0)<0和ΔrGm(1)> 0 成立时,根据零点定理和单调定理,反应系统存在唯一的化学平衡态ΔrGm(ξe) = 0。根据式(7),有:
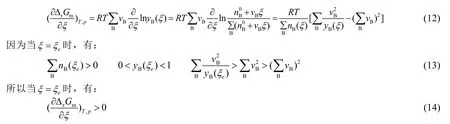
根据极值定理,G(ξe)不仅是吉布斯函数G(ξ)在开区间(0, 1)内的极值,而且是极小值。即在等温等压条件下,可以自发进行但又不能进行到底的理想气体或理想溶液反应系统,仅仅存在唯一的化学平衡态,而这个唯一化学平衡态是一个稳定的平衡态。
为了便于读者理解本文关于理想气体或理想溶液反应系统的化学平衡态的存在性、唯一性与稳定性的结论,下面给出理想气体或理想溶液反应系统的的示意图。
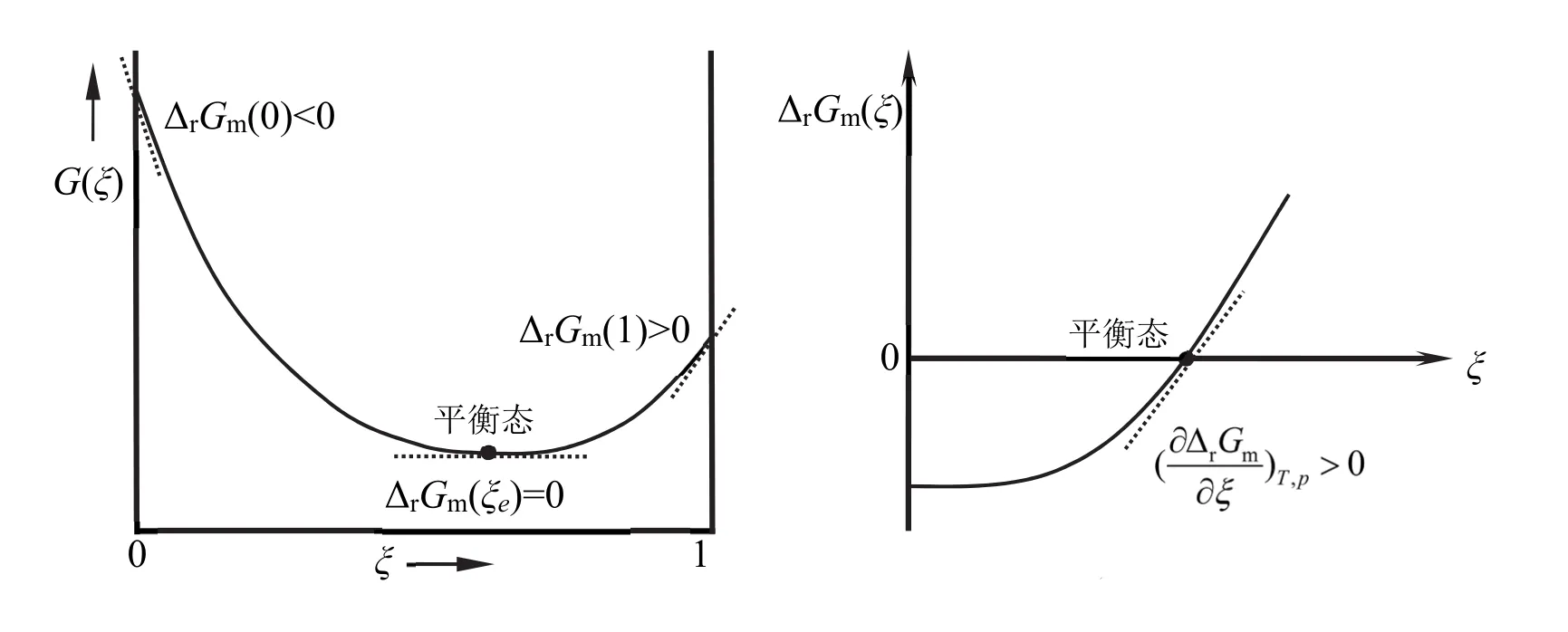
图1 理想气体或理想溶液反应系统的示意图
需要说明的是,本文选取理想气体或理想溶液反应系统为例,仅仅是因为理想气体或理想溶液反应系统的吉布斯函数G(ξ)及其一阶导数和二阶导数的数学表达式非常简单,便于读者理解。而绝不是说,本文关于化学平衡态的存在性、唯一性与稳定性的结论,仅仅只适用于理想气体或理想溶液反应系统。
5 结语
迄今为止,化学仍然还是一门以实验为主的学科,由于这种学科进化的阶段性所产生的局限性,导致目前许多重要的化学概念被认为是理所当然的或不言而喻的,很少进行过深入的理论分析和严格的数学论证,化学平衡态的存在性、唯一性与稳定性问题就是其中一例。本文把化学平衡问题数学化的最终目的就是使其结论具有普遍化的意义,所以本文关于化学平衡态的存在性、唯一性与稳定性的结论对于任何化学反应都是成立的。
致谢:作者曾就本文内容与山东大学张树永教授进行过有益的讨论,特此致谢。
