一种基于UWB的高精度室内定位系统设计

李玉峰，王君祎，李硕磊

(沈阳航空航天大学 电子信息工程学院，沈阳 110136)

基于位置的服务(Location-Based Service，LBS)已经在人类生活的方方面面扮演着重要的角色。目前，室外定位大多依赖全球卫星导航系统[1](Global Navigation Satellite System，GNSS)，由于卫星信号穿透建筑物的能力较差，一般情况下利用GNSS难以实现室内定位。目前主流的室内定位技术主要有WIFI、惯性导航及超宽带技术(Ultra-Wide Band，UWB)等。文献[2-3]提出了基于WIFI的定位系统，成本低且易部署，但是定位精度差通常在5～10 m左右；文献[4]提出了地磁和惯导的室内定位系统，该方法有效缩短了离线阶段基准库的构建时间，且定位精度提高到2 m左右；文献[5-7]提出了基于UWB的室内定位方法，UWB信号的脉冲功率谱密度极低，具有多径分辨能力强、抗干扰性好等优点，定位精度通常在分米甚至厘米级，是目前一种性价比较高的室内定位方法，故本文采用UWB技术来实现室内定位。

在实际定位场景中非视距误差以及多径效应会影响定位精度，针对此问题，刘琚等[8]提出了一种在非视距环境中的TDOA/AOA混合定位方法，相比于单纯的TDOA定位方法在一定程度上提高了定位的精度，但是随着AOA的测量精度下降，该方法的定位精度也会随之下降。毛永毅等[9]提出了面向室内定位的DHOHF-Elman神经网络算法，该算法能够较高程度地抑制环境中的高斯白噪声，但是定位精度受训练集影响大，且训练过程烦琐，不适合实际应用。李奇越等[10]提出了基于有色噪声自适应卡尔曼滤波算法，在一定程度上提高了定位精度，但是滤波效果容易发散，并且测量数据中的粗大误差对滤波结果影响大。文献[11-12]提出基于信道估计和地域规划的方法来抑制NLOS误差，该方法虽然可行但精度并不理想。为了降低NLOS和粗大误差对定位精度的影响，本文采用中值均值滤波法对原始距离观测量进行预处理，该方法能极大程度地剔除距离观测数据中的粗大误差，然后结合Taylor定位算法求解标签的位置信息，最后采用卡尔曼滤波算法进行滤波处理以抑制NLOS误差。实验表明该算法实现简单、定位精度高且实时性强。

1 UWB定位系统设计

本定位系统主要由定位标签(Tag)、参考基站(Anchor)、无线通信系统以及上位机等组成。其中定位标签和参考基站实现对配有定位标签的待测目标定位；无线通信系统主要将待测目标的测量信息传递给上位机；上位机显示平台主要包括基站、标签列表以及相关的配置信息，能够通过无线通信技术读取标签与基站之间的相对距离，并通过本文设计的定位算法求解位置信息，并将位置信息直观地显示在可视化界面上。同时为了应对定位场景的不固定问题，该上位机设有导入地图功能，实现不同场景下的定位。系统结构如图1所示。

图1 UWB室内定位系统结构图

2 硬件系统设计

硬件系统主要由UWB收发器、无线通信模块、主控单元、按键模块和显示模块等组成，系统框图如图2所示。其中UWB电路、主控单元以及通信电路的设计是该硬件系统的核心电路。

2.1 UWB电路设计

该系统采用DWM1000模块来实现UWB信号的接收与发送，该模块符合IEEE 802.15.4-2011的低功耗、低成本标准，其发射功率在-35～62 dBm/MHz区间。该模块集成了射频收发天线、电源管理和时钟等相关外围电路，使芯片体积小、集成度高且易于操作。在视距情况下，DWM1000测距可达290 m，非视距情况下测距可达35 m，其精度高达10 cm。同时设有3种数据传输速率可供选择，分别为110 kbit/s、850 kbit/s 和 6.81 Mbit/s，能够满足大部分场景的应用。该模块通过SPI总线与主控芯片进行通信，操作简单且数据传输速率高。DWM1000模块电路如图3所示。

2.2 主控单元电路设计

该高精度定位系统主控单元的最小系统电路如图4所示，主控芯片为STM32F103U8T6。该芯片采用arm架构，72 MHz最大时钟频率，配有专为要求高性能、低成本、低功耗的嵌入式应用设计的ARM32位Cortex-M内核芯片。根据本设计中定位及无线通信功能的实际需求，结合STM32单片机自身特点，编写软件程序实现UWB测距信息的获取、数据处理以及数据通信等功能。其内部集成的丰富硬件资源和灵活的库函数为本文提出的高精度定位系统的设计与实现带来了极大的方便。

2.3 通信电路设计

该高精度定位系统采用LoRa无线模块作为通信设备，该模块是一款基于SX1268射频芯片的无线串口模块，具有多种传输方式，且支持空中唤醒，非常适合超低功耗应用。该模块的载波中心频段为433 MHz，发射功率为100 mW，通信距离高达5 km。采用先进LoRa扩频技术，使其具有强干扰能力和穿透能力，较传统的FSK性能提升了1倍。本文主要采用LoRa模块实现UWB基站和标签与PC机的直接数据交互，在使用LoRa无线模块前先对其进行工作模式的参数配置，程序中对串口进行初始化设置，通过串口通信实现位置信息的传递。其接口电路如图5所示。

3 软件算法设计与实现

为克服非视距误差和随机误差等问题，本文采用中值均值滤波法对UWB观测距离进行滤波处理，然后对距离量进行判断，如果距离观测量的数量不满足taylor的定位算法输入量的个数，则返回继续观测，相反则通过taylor的定位算法求解位置信息，然后将此位置通过卡尔曼滤波再次进行平滑处理，最大限度地降低随机干扰带来的误差影响，算法流程图如图6所示。

3.1 Taylor定位算法设计

(1)

三维情况有

(2)

式中，(xn,yn,zn)为基站n的坐标值，dn表示待测目标与基站n之间的测量距离。

由Taylor级数展开并忽略二阶以上分量可得

(3)

式中，

(4)

(5)

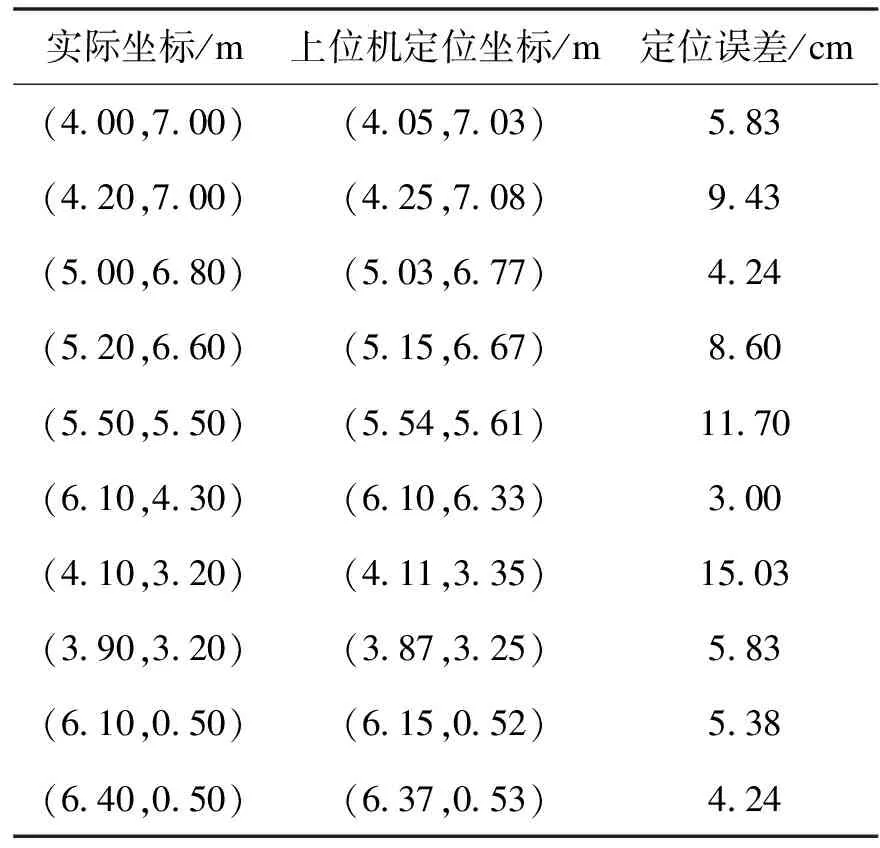
式中(x0,y0,z0)为上一次的迭代结果，每次迭代之后求出误差量Δx、Δy、Δz，并更新坐标值，进行下一次迭代。|Δx|+|Δy|+|Δz|

3.2 距离滤波算法设计

考虑到实际定位环境中由于脉冲干扰带来的测距误差，本文采用中值滤波法对距离观测量进行滤波，相比于传统的均值滤波算法，该算法能够极大降低由于脉冲干扰而引起的观测偏差，该算法将N次观测量进行大小排序，并剔除最大值和最小值，然后将剩余的N-2个观测量进行均值滤波，如式(6)所示。

(6)

其中，X(K)为观测量，且X(1)≤X(2)…≤X(N),N≥3。

理论情况下取任意值，但是N的取值过大不仅会影响运算速率同时会降低滤波效果的实时性，通常在实际情况中一般取4～6，本文N的取值为5，该滤波算法计算方便、速度快，同时尽可能保证了滤波的时效性。

3.3 卡尔曼滤波算法设计

虽然上文的距离滤波算法已经对距离观测量中由于脉冲干扰带来的误差进行了滤波，单定位结果仍会存在随机误差，因此本文采用卡尔曼[14]算法对解算后的位置信息进行滤波。卡尔曼是一种最优滤波器，采用递推算法，即由参数的验前估计和新的观测数据进行状态更新，一般只需存储前一个历元的状态参数估值，无须存储所有历史的观测信息，因此卡尔曼滤波具有很高的计算效率，并可以进行实时估计。

设状态变量n维，k时刻的状态为xk；k时刻的m维测量量zk,则

状态方程为xk=Øk-1xk-1+Γk-1wk-1

(7)

测量方程为

zk=Hkxk+Vk

(8)

其中Øk-1为状态转移矩阵；Γk-1为状态噪声系数矩阵；wk-1为状态噪声，Hk为测量矩阵；Vk为测量噪声，一般为零期望白噪声；根据匀加速运动模型有

(9)

(10)

(11)

由于系统采样频率较高，在一个采样周期内可以近似认为移动目标做匀速运动，因此上述公式可改写为

(12)

考虑到二维情形下的状态模型包含水平方向和垂直方向的位置和速度，因此可以将状态方程定义为

(13)

系统方程可以表示为

(14)

相应的测量误差方程和状态方程分别为

(15)

(16)

3.4 上位机软件设计

该上位机监测软件在挪威TrollTech公司出品QTCreator[15]平台上开发，是整个定位系统的信息处理中心，能够通过LoRa无线通信系统接收待测目标发送的距离信息，并结合上文提到的定位算法进行位置解算，上位机软件界面如图7所示。

图7 上位机软件界面

如图7所示，地图显示区域主要用于显示待测目标的位置信息，控制菜单栏主要用于控制软件的开始和退出基本控制操作，初始化信息配置栏主要用于配置基站的坐标信息和导入环境地图，上位机软件设计流程图如图8所示。

图8 上位机软件设计流程图

为实现上位机软件，采用模块化的思想进行开发，运用信号与槽的机制实现各个组件之间的交互，使得软件开发变得更加直观和高效。同时采用C++模板以及异步调用的机制实现一款通用的后台处理应用框架，使其具有易于扩展、移植等优点。

4 实验验证与结果分析

4.1 软件算法测试

4.1.1 距离测试

在测试定位算法性能之前先对距离滤波算法进行测试。本文对基站与移动标签之间不同距离进行大量实验测试，如图9a所示为理论距离为5 m的500组距离观测量，可以看出在实际测试环境中，传感器的观测距离会有粗大误差存在，势必会对定位结果带来较大的定位误差。为了验证中位值均值滤波算法的性能，将500组距离观测量通过该算法进行滤波。本文选取5次观测量进行处理，因此500组观测数据经处理生成100组数据，如图9b所示，观测量中的粗大误差被有效剔除，测距精度有明显提高，测量误差由原来的22 cm降低到7 cm，为高精度定位提供了保障。

图9 距离观测值滤波前后测量结果

4.1.2 定位算法测试

本实验主要是对移动终端进行多点测试，同时将taylor、taylor+卡尔曼、中位值均值滤波+taylor以及中值均值滤波+taylor+卡尔曼4种算法通过多个位置点的定位结果进行对比分析，采用均方根误差(Root Mean Square Error，RMSE)来衡量定位精度，用(x,y)表示待测点的真实位置，(x′,y′)表示定位算法解算出来的位置坐标，则在二维坐标下有

(17)

本文对不同定位点进行了大量的实验测试，并选取图10所示路线进行算法对比，测试环境中基站的坐标分别为(0,0)、(10,0)、(10,10)、(0,10)，虚线为行驶路径，即A(2,8)→B(8,8)→C(8,7)→D(5,7)→E(5,0.5)→F(2,0.5)，不同算法定位结果如图11所示。

图10 测试路线

图11a所示的定位结果是距离观测量没有进行滤波处理而直接通过taylor算法进行定位的结果，由图可以看出定位结果误差大，且部分定位点存在粗大误差。图11b所示的是图11a的定位结果经过卡尔曼滤波后的定位结果，可以看出卡尔曼滤波算法虽然提高了定位的平滑性，但是受粗大误差影响大，从而影响滤波性能。图11c是将距离观测量通过本文设计的滤波算法处理后再进行Taylor定位的结果，定位结果的粗差被有效剔除，同时定位精度也有一定的提高，但提高幅度相对不大。图11d表示的是将图11c的定位结果进行卡尔曼滤波的定位结果，可以清晰地看出定位精度有明显提升，且能够较好地避免粗大误差带来的影响。表1给出了不同定位算法的定位精度，由表1可知，相比其他定位算法本文设计的算法定位精度更高。

图11 不同算法定位轨迹图

表1 不同算法定位精度对比

本文算法与常见的UWB定位算法定位精度对比如表2所示。

表2 本文算法与常见UWB定位算法精度对比表

由表2可知传统的最小二乘定位算法的定位精度为39 cm，扩展卡尔曼定位算法定位精度为33 cm，且容易受到环境中多径效应、随机噪声和非视距误差等因素的影响，本文提出的定位算法定位精度为12 cm，能够有效克服定位环境中的干扰，较最小二乘和扩展卡尔曼定位算法精度有显著提高。

4.2 上位机软件测试

在上位机软件正式测试之前需对此软件进行初始化配置，主要包括通信设置和基站坐标设置，然后开启定位系统，并对植入改进版卡尔曼定位算法的上位机定位观测软件进行测试。

由定位软件显示可以看出该定位系统对移动目标有良好的跟踪性，表3给出了部分测试数据与实际坐标的对比数据。

由表3数据得出本文设计的定位系统的定位轨迹与实际坐标高度吻合，实现了高精度定位，同时该软件更加直观高效地显示出了移动目标的运动轨迹，有较高的使用价值。

表3 部分上位机测试结果

5 结论

本文采用中值均值滤波算法对UWB距离观测量进行滤波，使得测距误差从22 cm降低到7 cm，同时有效消除距离观测量的粗大误差，使得Taylor定位结果的最大误差从1.4 m降低到30 cm，避免了粗大误差对卡尔曼滤波算法的影响，定位精度提高到12 cm。基于本文设计算法的上位机软件具有人机交互性好、操作简单、实时性强等优点，定位轨迹高度贴近真实轨迹，能够用于高精度定位领域。