高边坡预应力锚索格构梁极限抗力分析

唐 浩

（广东省有色金属地质局水文地质队，广东 广州 510800）

0 引言

预应力锚索格构梁是一种新型的高边坡支护措施，以挡土墙或是抗滑桩作坡脚，借用锚索和抗滑桩所构成的固相力[1-2]，来抵抗边坡的边坡推力或边坡土体的侧向土压力。与传统加固方法相比，预应力锚索格构梁属于主动加固方式[3]。像这样类似复合结构的出现，要比其余应力分析更加烦琐。所以，深入探讨预应力锚索格构梁的设计和支撑构架，对其内部参数做出优化，不仅会使设计更合理，也促进了这种新型支护加固体系在国内的发展和应用，推进了国家的工程建设。

1 预应力锚索格构梁极限抗力分析

1.1 格构梁内力计算

应力锚索结构是一种新型的挡土结构，其广泛应用于铁路、高速公路等部门的边坡处理和边坡加固[4]。其主要用于治理滑坡地质灾害中，也可用于加固潜在不稳定的边坡和地面斜坡，避免斜坡松散，用于破碎基岩斜坡时可以单独使用，也可以结合其他常用围护结构[5]。格构梁结构根据所用材料的不同，可分为砌体结构、现浇钢筋混凝土框架结构和预制预应力混凝土框架结构[6]。预应力锚索格构梁作为一个在节点处承受张拉应力的框架，是一个非常烦琐的系统构架。如图1 所示。若想对预应力锚索格构梁进行剖析，要好好研究空间内框架的结构，结构的锚固力和地基的稳定性等因素造成的共同影响。

图1 格构梁受力简图

以上设计的具体计算内容，首先要对锚索格构梁的框架分类，可以分成横梁和竖向肋两种，然后分别进行设计，在设计完成之后做出计算，计算式要对梁和垂直肋上的锚固力分布情况进行解析。可岩土体存在一定的复杂因素，只能根据地基的状态建立简单的模型，想找到一个合适全部土体的应力变化关系的数学模型是不容易的。将格构梁视为柱下的横条形基础，根据弹性基础梁节点系数分布法计算格构梁和竖向梁中锚索力的内力分布规律如公式（1）所示。

Fcos（90°-α-θ）=Fx+Fy（1）

式中：θ为锚固角，F为作用在节点上的锚索拉力，α为边坡角，Fx+Fy为分配在节点x，y方向上的锚索力荷载总数。考虑基础与格构梁的相互作用，假定基础的反力为线性分布，将格架梁锚头的交点作为固定端，在柱基反力的作用下计算格构梁的内力。最大极限底反力公式如公式（2）所示。

式中：B为梁的宽，L为梁的长，∑ p为格构梁上的合力，∑M为格构梁上的合力距。在中小型工程简化中，一般采用倒置梁法。与静定方法相比，倒梁法假设基底应力是根据线性分布的，通过分析基础和演绎统一反应的外部载荷，不考虑基础与基础梁相互作用的多跨连续梁内力分析。

1.2 格构悬臂段、锚索锚固段长度计算

在边坡加固设计过程中，为了避免末端反力的集中，格构梁通常从墙角锚索处延伸一定距离，称为悬臂截面。悬臂段长度对地基反力分布有重要影响。格构梁的合理悬臂长度不宜过小，而使格构梁端基础反力急剧增大，也不宜过大，使格构梁端基础反力过小而影响加固效果。控制悬臂截面保持在合理的长度，使格梁端部基础反力保持在中间格梁端部基础反力0.5 倍以内。为了测量加固体的剪应力，通常在加固体上附加阻力丝。锚索受力筋的拉伸力由剪切力进行平衡，进而求出实测应变中黏接面上的剪应力，如图2 所示。

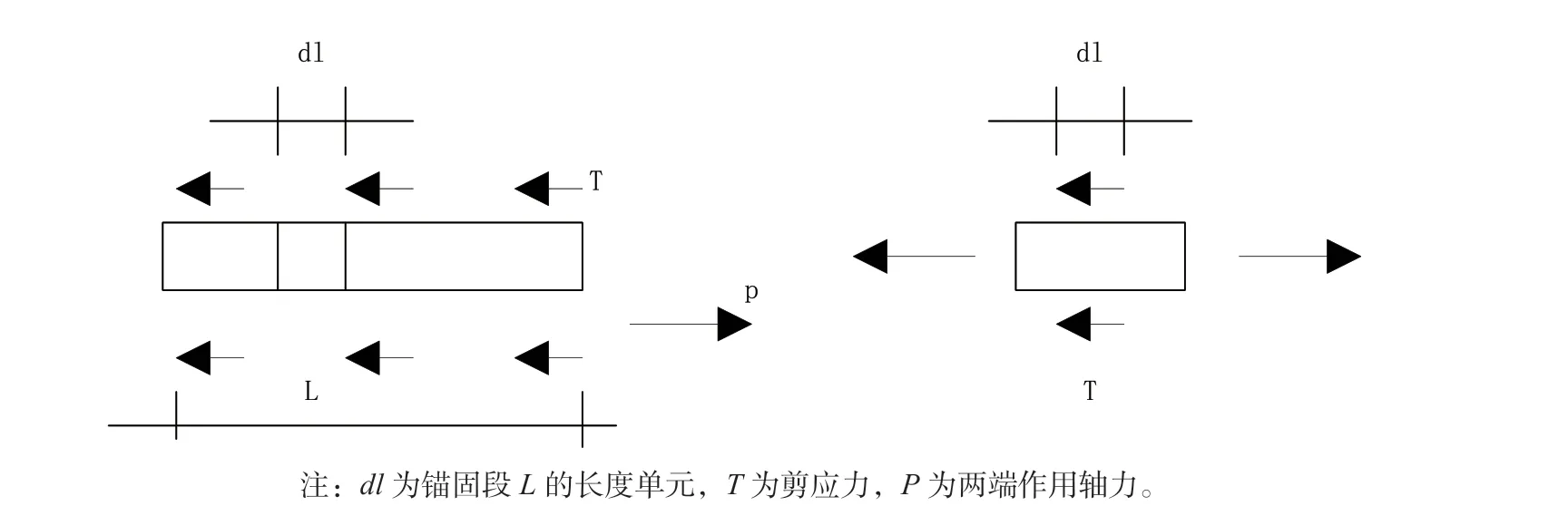
图2 锚索受力筋的受力分析

考虑到岩石和土壤的性质以及锚固体直径对应力分布的影响，可以得知硬岩体是可以选择粗直径和短锚固段的，而软岩体可以选择细直径和长锚固段。这样可以充分发挥锚索的承载能力。由力的平衡得到公式（3）。

式中：D表示锚段上的直径，dl表示锚固段长度，τ表示锚端dl上的平均剪应力。对钢绞线，πD为与注浆体接触的周长。由弹性力学δ=E·ε知：

式中：pi和pi+1为位于dl锚固段两端的作用轴力，εi以及εi+1为dl两侧的实际应变力，E为受力筋的弹性模量，F为受力筋的横断面积。则dl段上的平均剪应力如公式（5）所示。

式中：当受力筋上的拉力与应力平衡时，就可以按照εi-εi+1，求出剪应力的平均值τ，其他平均剪切应力可从式（5）中求出。用最小二乘法对一系列计算的剪应力进行处理后，可以得到接头表面相对一定张力的剪应力分布。在每步增加锚杆的拉力，可以得到锚固段长度的分布。

注浆体与孔壁的平均黏结强度如表1 所示。

表1 注浆体与孔壁间的结合强度

注浆体与加固体的平均黏结强度如表2 所示。

表2 注浆体与受力筋间的结合强度

钻孔的方法以及在钻孔时存在的冲击强度，决定了剪切强度的平均值。孔壁由于太过光滑，在冲击钻孔时注浆体与孔壁的连通性，关键体现在两者之间的黏结性。在冲击钻孔的过程中，孔壁表面变得粗糙，注浆体顺缝隙灌入，摩擦力受到了抗剪强度的限制，与黏结力相互作用构成了锚固力，使平均抗剪强度更大一些。

1.3 预应力格构梁极限抗力计算

预应力锚索加固是将锚索锚固在岩土体内，利用深部土体自身的强度，在岩土工程中直接制作预应力锚杆是人为施加外力的一种方式，使不稳定滑动体在高围压下呈现三维应力状态，提高岩土强度，改善变形特性。由于预应力的作用，岩体结构处于角压实状态，使岩土体压缩完整，锚固力改变了滑动面上的应力，锚索锚固力增加，格构梁极限阻力P可由公式（6）计算。

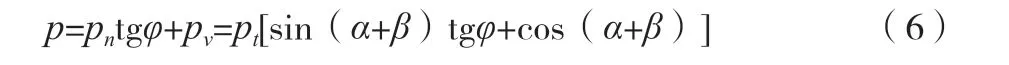
式中：pn为滑动面上的分力，pv为滑动面上的切向力，α为倾角，β为水平方向上存在的夹角，φ为靠内侧的摩擦角。

预应力锚索可以直接在滑动面上作用，从而产生一定的滑移阻力。另一方面，可以在滑动面上增加法向应力，这样就可以提高格构梁的极限阻力。预应力格构梁极限抗力设计，应考虑施工条件的影响、治理结构及整体经济性这三个方面的因素，在这三个条件全部满足的情况下，锚固角才能成为最优锚固角。实际工程中，锚固胶的应用受到各种条件的制约，锚杆的数量是有限的，而且工艺也有限制，锚杆不可以太大太长。也就是说，锚固力受到了限制，但为使滑体更加稳定，提高锚杆的利用率可以使每个锚杆给予最优抗滑力，从而利用格构梁的极限阻力进行整体设计，使整个过程更加完美。

设计锚索前详细研究边坡结构和地质条件，尤其是滑移面的相关参数。在此基础上，从预应力锚索对滑动面提供的抗滑能力、锚索长度、锚杆强度等方面进行综合计算，确定了加固效果好、经济的预应力格构梁的极限阻力角。提高边坡治理整体上的经济性和效果。

2 实例试验

2.1 试验准备

某边坡高度约为7.8m～15.7m，边坡约为35°～65°，边坡不同部位差异较大，原有挡土墙在拆除施工过程中已经倒塌，边坡现处于不稳定状态。边坡设计高度为14.5m～19.0m，为开挖和填筑边坡，边坡的顶部和底部均规划建造房屋。按照《建筑边坡工程技术规范》和《工程岩石分类标准》为工程支护设计提供岩土参数建议值边坡段压实填土参数可根据表3 进行选择。

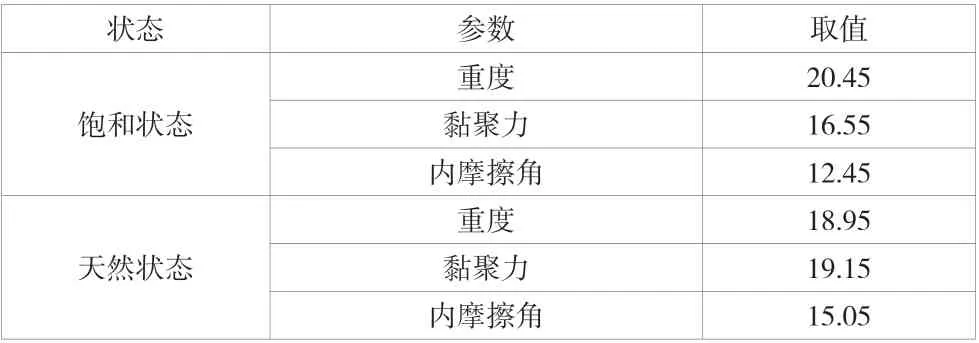
表3 压实填土计算参数取值表

边坡土体揭露深度为26.85m。表层充填人工土，下部为侏罗系木坡组的黏土、砾质土和粉砂岩。

锚索格构梁挡土墙体系预压试验主要包括静止土压力试验、竖向土压力试验、锚索张拉试验、格架横梁试验、竖向梁截面锚索应力试验。充填回填土是造成压力变化的原因，施工条件或天气变化也会有所影响，如张拉过程、降雨、冻结等工作条件。充填体回填后压力不是恒定的，而是随时间变化的。在可计算的节点总数上划分网格时，也减少了计算时间，使划分网格时将土体应力集中在锚索附着的网格上。挡土墙附着土体的网面宜细，但原锚索支护结构的部分土网宜稀。具体实体模型如下:板网尺寸为0.4m，底部抗滑土网尺寸为0.45m，锚索格构梁挡土墙附近土网为0.87m，模型边界支撑结构的网格尺寸为4.55m。

网格控制的土壤切分线梯度为0.7m～5.0m。为研究斜预应力锚索格构梁和直预应力锚索格构梁极限阻力挡土墙受力和变形的特殊点，分别建立了倾角为75°和85°的预应力格构边坡模型。锚索格构梁边坡支护的网格划分原则及竖向预应力，与倾斜的斜坡和直线垂直坡相比，向外水平土压力的变化规律和水平位移的变化规律不同。与边坡倾斜角度85°相比，当锚索边坡倾斜角度75°时，锚索具有更大的张力、格构梁铺设和固定更紧密。此外，当坡度为75°时，锚索提供的轴向力也较大，说明锚索接触面上的摩擦力更均匀。预应力锚索格构梁施工完成后，水平位移随墙体高度的变化而变化，当格构梁为垂直和直线时，挡土墙中部存在15.3mm 的正位移。

2.2 试验结论

格构梁的水平位移表现出一定的锯齿状，这是由于锚索的负位移较大，而锚索间土层的作用使负位移减小。而在垂直格架梁支撑形式下，这种现象并不明显，如图3 所示。

图3 格构梁水平位移变化图

因为锚索的负位移加大，锚索间土层负位移变小，所以格构梁的水平位移表现出锯齿状，在垂直格构梁支撑形式下并不明显。网格梁的顶部弯矩距离比较小，底部弯矩相对来说比较大，与此同时顶部与底部抗滑桩的交点处弯矩达到抗力的极限点。与之前研究的垂直和直格梁支撑的支挡形式相比，格梁仅在上弯矩下存在反向弯曲点。当网格梁倾斜角为75°时，底部弯矩较大，可达685.5kN·m。

水平土压力直接作用于挡土墙上，直接影响挡土墙的稳定性，也决定了格构梁的极限抗力。水平应力的方向为负，说明此处土单元的水平力是用来压实墙板的。当格构挡土墙垂直且格构梁高度大于3m 时，格构挡土墙后土体的水平应力大于斜挡土墙后土体。当格梁高度小于3m 时，斜格梁墙后的静止土压力大于直墙后的水平土压力，当倾角为75°时，格梁后的静止土压力最大。

3 结语

因为结合锚索支护和格构梁的特点，预应力锚索框架梁结构属于新型支护结构。这种结构的设计理论和规范虽然还不完善，但是在边坡工程中已经得到了应用。想要得到预应力锚索格构梁的应力分析，就应该与预应力锚索墩的支护分析以及预应力锚索肋梁的应力做对比，提供一些参考依据作为优化数据。为得到更多的数据作样本分析，对格构梁的间距进行调整，并模拟了多种工况下的应力数值，与实际情况结合，从而将得到的数据作为设计优化参考的依据。在现阶段，框架式格构梁的结构计算都是将格构梁拆分，分别计算横向、纵向格构梁。在拆分的过程里，一般都会对交叉结点处的横梁与纵梁铰接作出假设，这样很容易忽略另外一个方向上的格构梁以及扭转角在另一个方向格构梁上产生的扭矩影响，因此，需要对格构梁上的扭矩影响进行进一步探索。