基于α法的离散时间线性时不变系统状态超调优化1
2021-02-10程福亨龙达峰
程福亨, 龙达峰
(惠州学院 电子信息与电气工程学院,广东 惠州 516007)
调节器设计是控制领域的基本问题,经过几十年发展,相关理论和方法日渐完善[1-2].随着优化控制的发展,线性二次调节器(Linear quadratic regulator, LQR)设计理论为调节器设计提供了一种很好的方案.最近十几年,不少研究围绕改进现有的调节器设计方法或者把这些方法应用于某些特殊系统[3-5].在离散时间线性系统的LQR设计理论中,优化目标是各时刻状态、输入的二次函数之和,因此不能用于优化诸如最大状态范数等单个值的情况.
超调量最早见于经典控制理论,并被用于度量阶跃跟踪时最大输出与最终输出的差相对最终输出的大小,人们曾经对线性系统阶跃跟踪时的超调优化问题进行了大量研究[6-11].在调节器设计中,对于任意非零初态,要求设计合适的控制输入,使得系统状态逐渐趋近于原点.显然,从0时刻开始趋于原点的过程中,系统状态的范数一般呈现非单调变化.若把此过程中状态最大范数与初始状态范数之比称为系统状态调节过程中的超调量,并作为优化目标,这是完全不同于LQR设计方案和跟踪控制的超调优化问题,并且具有理论和实际意义.
近年来,复杂非线性系统的优化问题是一个研究热点[12-14].但是,线性系统的优化问题仍是基本问题,并在一定意义上有助于非线性系统优化研究.本文在研究固定α法特性的基础上,把该方法应用于离散时间线性时不变系统状态调节过程中的超调优化,并给出了相应的设计过程.随着状态的演变,对于不同的当前状态,若α取使得下个时刻状态范数最小的值,或许可以进一步优化状态超调量,从而提出了动态α法,并且,以一类4阶系统为例,研究了采用动态α法必然比采用固定α法可以获得更小超调的数学条件.
1 问题描述及预备知识
文中用到的符号说明如下:
ℝ:实数集;
ℝn:n维实向量集或n×1实矩阵集;
ℝn×n:n×n实矩阵集;
PT:矩阵P的转置矩阵;
P-1:可逆矩阵P的逆阵;
xT:向量x∈ℝn的转置向量;
xi: 向量x∈ℝn的第i个分量;
‖x‖:向量x的2-范数;
0:合适维数各元素都为0的列向量;
E:合适阶数的单位矩阵.
考虑下式描述的n-阶单输入可控离散时间线性时不变系统:
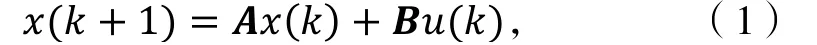
其中,x k ∈ℝn是系统状态,u k ∈ℝ是系统输入,A∈ℝn×n和B∈ℝn×1分别是系统矩阵和输入矩阵.
我们用状态2-范数度量系统(1)状态调节期间的超调量.由于2-范数的齐次性,只需要考虑n维单位球面上初态的超调量,则系统(1)在状态调节期间的状态超调优化设计问题描述如下:
对于n维单位球面上的给定初态x 0 ,设计一个控制输入u k ,使得系统状态向原点趋近过程中的最大状态2-范数最小化,即

定义1 对于某个给定的初态x 0 ,如果有一个控制输入u kx0,使得

则称系统(1)在初态x 0 可以无状态超调;否则,称 η-1 ×100%为系统在初态x 0 的状态超调量,所有的无超调初态形成系统的无超调区域,如果系统的无超调区域覆盖整个状态空间,则系统是状态无超调的,否则称

为系统的状态超调量.
2 基于α法的离散时间线性时不变系统状态调节优化设计
2.1 固定α法的基本原理
对于系统(1),令
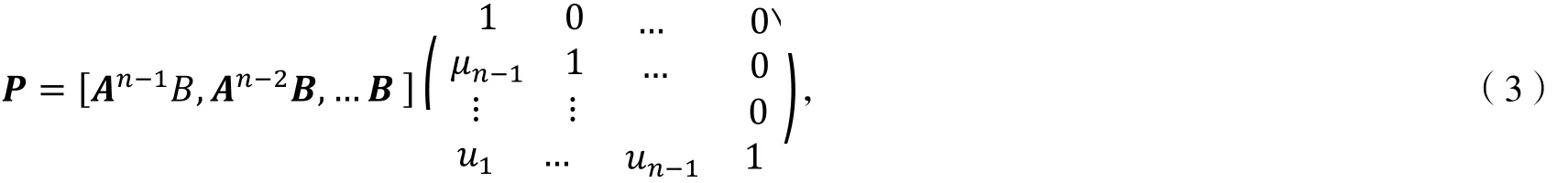
其中,μ1、μ2、…,μn-1是如下特征多项式的系数,
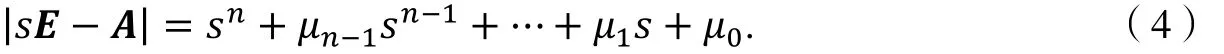

其中

直接计算可知:


进一步,如果

因此,控制输入(8)使得系统状态2-范数随着时间广义单调递减. 随后,把这个方法称为固定α法.
2.2 固定α法的特性
为了设计一个控制输入使得状态调节过程中的超调量尽可能小,下面研究固定α法的一些特性.
定理1对于一个n阶系统(1),自0时刻起,如果每n个连续时刻视为一个周期,那么2个相邻周期相应时刻的状态2-范数具有如下关系

证明:显然,

同时,把控制输入(8)式代入系统的可控标准型(5)式,可得,

把式(11)代入式(10)并简化即得结论. 证毕.
根据定理1,当k→+∞时,‖x k ‖的最大值必然出现在k∈ 0,1,…,n-1 . 因此,为了使得系统(1)在状态调节期间的状态超调最小,只需
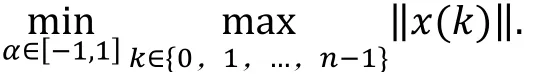
定理2对于一个给定初态x 0 ,如果系统(1)的控制输入如式(8)所示,那么当k=1,2,…,n-1时,‖x k ‖2是常数,或者是关于α的开口向上的二次函数.
证明:根据向量的加法特性,有

因此,

对于给定系统及初态,akTPTPak、akTPTPbk和bkTPTPbk都是常数,因此,从数学形式上看,‖x k ‖2是关于α的开口向上的二次函数.
同时,对于给定的非零初态x 0 ,x¯ 0 =P-1x 0 也是非零向量.
此外,由于矩阵PTP正定,则这些二次函数的图像开口都向上. 证毕.
2.3 基于固定α法的状态超调优化设计
结合固定α法及其性质,可以构造出系统(1)的一种状态超调优化设计方案.
对于给定的系统(1)及初态x 0 , ‖x 0 ‖2随之确定,但是,当k∈ 1,2,…,n-1 时,‖x k ‖2是一个常数或者关于α的二次函数. 如果存在某个α,使得
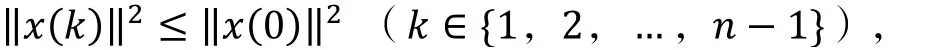
则根据定义1和定理1,系统在状态调节期间一直无超调.
如果

那么系统对于初态x 0 必然存在调节超调量. 在这种情况下,为了实现最小超调,α应该取使得
综合上述分析,可以给出基于固定α法的状态超调优化设计步骤如下:
步骤1:对于给定初态x 0 ,依次算出‖x k ‖的表达式,其中k∈ 1,2,…,n-1 .
步骤2:根据定理2,有如下2种情况:
情况(i):当α∈Θ1⊆ -1,1 时,‖x k ‖2≤‖x 0 ‖2成立,则系统(1)在初态x 0 下采用式(8)所示的控制输入时无超调. 此时,为了使得状态尽快收敛,取|α|尽量小的α值.
情况(ii):

成立,则该初态时系统(1)采用式(8)所示的控制输入时存在超调. 此时,为使得状态尽快收敛,也取|α|尽量小的α值.
步骤3:把步骤2中得到的α代入式(8),即得到实现超调优化的控制输入.
在步骤2中,直接人工确定Θ1、Θ2和找到最优的α颇有难度,Matlab软件提供的多目标优化函数fminimax可以方便的用于解决这个问题. 但是在使用fminimax时必须特别注意,该函数是在闭区间[-1,1]上搜索最优的α,如果找到的最优α为1或者-1,此时尽管采用式(8)所示的控制输入使得超调最小,但是状态2-范数呈现等幅振荡,这显然是不合期望的,因此,式(8)中的α应该取接近于所搜索到的1或者-1,但是绝对值稍微小于1的数,这将使得系统超调稍微增加一些,但是能保证状态最终向原点收敛.
2.4 动态α法及其在一类四阶系统中的应用
在固定α法中,参数α的值与初态密切相关,并且在整个状态调节期间是常数. 通常,状态随着时间演变,在不同的当前状态,如果式(8)所示的控制输入中的α取使得下一时间状态2-范数最小的值,系统状态超调可能进一步下降,而且系统状态可能更快收敛,这个方法称为动态α法. 显然,该法属于“贪婪算法”. 下面以四阶可控系统为例来讨论在什么情况下,动态α法可以比固定α法获得更小的状态超调量.
对于一个给定的四阶可控系统及初态x 0 ,令αc表示采用固定α法时参数α的值,‖x k ‖2表示固定α法中k时刻状态2-范数的平方,而αk和则依次表示采用动态α法时k时刻参数α的值和该时刻状态2-范数的平方. 则有

根据αc和α1的定义,可得,

对于四阶可控系统,有如下计算结果,
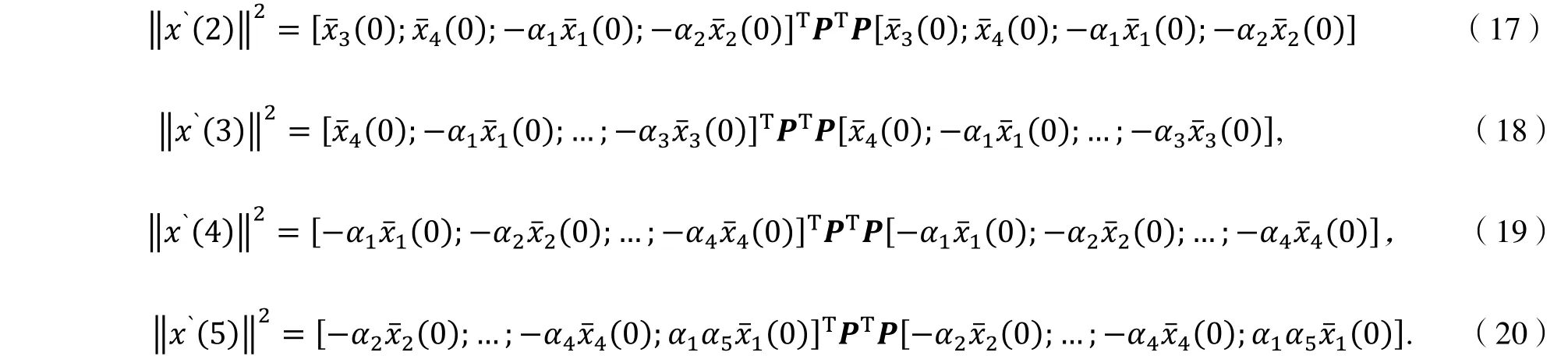
在固定α法中,‖x k ‖2是常数或者关于α0的二次函数.根据定理2的证明过程可知,‖x k ‖2是常数,当且仅当0 =0 =…=0 =0,并且,如果‖x k ‖2是常数,则当i=1,2,…,k-1时,‖x i ‖2都是常数.
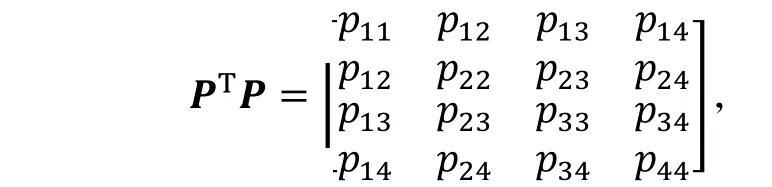
假设1:p14=p34=0,|p24|<|p44|.
根据实对称正定矩阵的性质,p44>0. 当k=1,2,…,6时,的对称轴依次为,

据以上规律,当k≥7时,可以猜想出αk的表达式,并用数学归纳法证明,在此省略.
命题1在假设1的条件下,
证明:对于任意给定的初始状态x 0 , 根据式(21)可以得到α1和α2. 令,根据假设1,|β|<1. 当k=1,2,…时,令αk与αk+2相乘,可得αk+2=-β2∈ -1,0 . 证毕.
在固定α法中,为了使得状态2-范数收敛到原点,αc∈ -1,1 是个常数. 然而在动态α法中,参数αk随着当前状态发生变化, 其中一些|αk|可能大于或者等于1,但是不可能所有的|αk|都大于或者等于1,正如上面推导所示,|α1|和|α2|可能大于或等于1,而当k≥3时,|αk|∈ -1,1 , 这是随后命题3证明中用到的一个关键条件.
假设2:p13==p23=p24=p33=0,-2p24α02β2-p22α02+p22β4≤2p24α0β2.
命题2在假设1和假设2的条件下,
证明:根据式(16)和假设1,可得

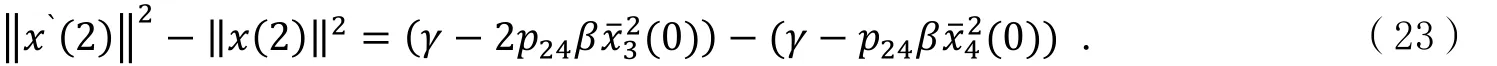

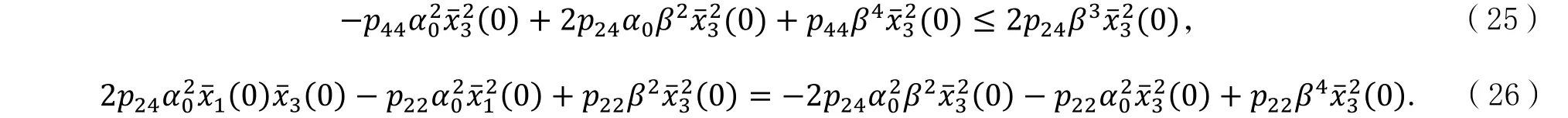
并且,此时假设2中的不等式变为

假设3:p12=0, p44β2-2p24β+p11>0.
命题3在假设2和假设3的条件下,当k≥3时,
证明:首先,当k≥3时,一方面,在命题1中,已经证明,αk=-β2∈ -1,1 是常数,另一方面,根据定理1,此时. 因此,只需要证明当k=3,4,5,6时命题中的不等式成立. 令ρ=p44β2-2p24β+p11, 可依次算得如下结果,
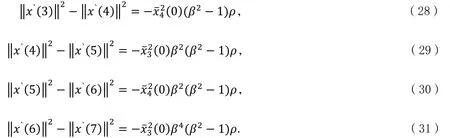
式(28)~(29)子等号右侧部分都大于或者等于0,因此,当k≥3时,. 证毕.
综合命题2和命题3,可得

可见,对于满足以上3个假设的四阶可控系统,动态α法比固定α法可以获得更小的调节超调量.
3 验证算例
考虑具有如下系统矩阵和输入矩阵的系统(1),对于本系统,对应的PTP为


不难验证,3个假设都成立,对于如下2个给定初态,

依次采用固定α法和动态α法时的控制输入和状态-2范数分别如图1、图2所示,可见,对于这2个初态,动态α法都比固定α法可以获得更小的调节超调量.并且,对于初态x 02,为了获得小的调节超调量,固定α法使得状态2-范数呈现等幅振荡,而动态α法不仅获得更小的超调量,还能使得状态快速收敛.
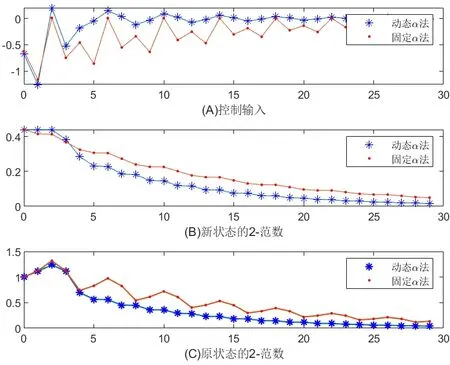
图1 初态为x 0 1时的控制输入及状态2-范数演变过程

图2 初态为x 0 2时的控制输入及状态2-范数演变过程
4 结论
对于离散时间线性时不变系统的调节超调量优化问题,固定α法具有一些非常漂亮的特性,基于这些特性可以设计出调节超调量优化的控制输入.尽管动态α法是一种“贪婪算法”,但是对于满足一定条件的四阶可控系统,动态α法在降低调节超调量和提高收敛的快速性方面优于固定α法.
