隧道掘进对近接垂直交叉隧道的三维有限元分析
2021-02-09赵俞成艾兵兵刘东宋强冯伟艾志伟
赵俞成 艾兵兵 刘东 宋强 冯伟 艾志伟
摘要:為研究隧道施工顺序对隧道开挖的影响,采用三维有限元分析方法模拟某垂直穿越隧道的开挖过程.基于砂土的亚塑性本构模型并考虑土体的小应变刚度,分析施工顺序对垂直交叉隧道的影响,研究对既有隧道附近土体的应力传递机制.研究结果表明:与无既有隧道工况相比,既有隧道的存在使得最大沉降量降低14%;新建隧道在既有隧道上方时,地表沉降较大,但影响范围小,当掌子面接近既有隧道中心线时,既有隧道的应力由拱顶传递至拱肩;当掌子面距离既有隧道中心线后方3D和前方6D之间时,应力释放对既有隧道的影响显著;新建隧道在既有隧道下方时,既有隧道产生的变形和弯矩更大;在垂直交叉隧道施工中,应充分考虑施工顺序对地表沉降、既有隧道的影响.
关键词:隧道开挖;垂直交叉隧道;地表沉降;隧道变形;应力传递机制;数值分析
中图分类号:TU43文献标志码:A
基金项目:国家自然科学基金资助项目(51779221,51939010),National Natural Science Foundation of China(51779221,51939010);浙江省重点研发计划项目(2018C03031),Key Research and Development Program of Zhejiang Province(2018C03031)
Three-dimensional Finite Element Study of Tunnel Advancing to Adjacent Perpendicularly Crossing Tunnel
ZHAO Yucheng1,AI Bingbing2,LIU Dong2,SONG Qiang2,FENG Wei3,AI Zhiwei3
(1. Research Center of Coastal and Urban Geotechnical Engineering,Zhejiang University,Hangzhou 310058,China;2. Project Department of Hangzhou Metro,China Railway NO.2 Engineering Group Co Ltd,Hangzhou 310058,China;3. Hangzhou Metro Group Co Ltd,Hangzhou 310058,China)
Abstract:In this study,a three-dimensional finite element analysis method was used to simulate tunnel excava-tion nearby a perpendicularly crossing existing tunnel,in order to investigate the effects of construction sequences on cross-cutting tunnels. The hypoplastic constitutive model of sand and soil is adopted and the soil small-strain stiffness is considered in the numerical analysis,so as to study the effect of construction sequences on cross-cutting tunnels as well as the stress transfer mechanism of the soil near the existing tunnel. The results show that the existence of the ex-isting tunnel reduces the maximum settlement by 14% when compared with the condition without the existing tunnel; when the new tunnel is above the existing tunnel,the settlement is larger,but the impact range is smaller. When the tunnel face approaches the centerline of the existing tunnel,the stress of the existing tunnel is transferred from the vault to the abutment;when the tunnel face is between 3D behind and 6D in front of the centerline of the existing tun-nel,the effect of stress relief on the existing tunnel is significant; when the new tunnel is under the existing tunnel,the deformation and bending moment of the existing tunnel are greater. In the construction of vertical cross tunnels,the impact of the construction sequence on the ground settlement and the existing tunnel should be considered comprehen-sively.
Key words:tunneling excavation;perpendicularly crossing tunnels;ground surface settlement;tunnel deforma-tion;stress transfer mechanics;numerical analysis
近几十年来,研究土体-隧道相互作用的方法多种多样,包括现场监测、模型试验、经验/分析方法和数值模拟[1-5],然而,大多数研究集中在平行隧道和背驮式隧道,对垂直交叉隧道研究较少.此外,大多数研究使用简单的弹性-理想塑性本构模型对隧道相互作用进行数值分析[6-9],没有考虑由于应力增加导致土体剪切模量的改变以及刚度的变化.基于速率型张量函数建立的亚塑性模型能够更好地描述土体复杂的本构特性[10-11].因此,有必要应用砂土的亚塑性本构模型研究垂直交叉隧道施工过程对邻近既有隧道的影响.
关于垂直交叉隧道的研究有限. Kim等[12]在1g条件下进行了模型试验,研究了粘土地层中新建隧道对既有隧道的影响.在垂直交叉隧道中,衬砌变形和弯矩在隧道开挖的初始阶段有明显的变化.由于试验是在1g的条件下进行的,原型尺度下的实际应力状态不能被复制,因此不能很好地反映土的剪胀行为. Liu等[13]采用三维有限元分析方法,研究了在新建隧道上下垂直施工时,隧道开挖对既有隧道的影响.衬砌在拱脚处受拉,而在拱顶和仰拱处受压.但该项研究未对既有隧道附近土体的应力传递机理进行研究. Ng等[14]在60g条件下开展离心机模型试验,并基于砂土的亚塑性本构模型采用有限元分析方法,研究了隧道竖直间距与直径之比(P/D)对垂直交叉隧道相互作用的影响.当P/D较小时,既有隧道中心线处的沉降较大.但该研究未考虑垂直交叉隧道的施工顺序对既有隧道的影响. Wang等[15]开展了两组离心机模型试验,研究了干砂中现有隧道的形状(圆形和马蹄形)对垂直交叉隧道相互作用的影响,并使用PLAXIS 3D进行三维数值反分析,但未考虑新建隧道上穿的情况.
目前,鲜有研究涉及砂土中垂直交叉隧道的施工顺序对既有隧道的影响.不同的隧道施工顺序引起不同的地应力变化,从而引发不同的应力传递机制.这导致了不同的地表沉降和变形,从而引起隧道衬砌产生不同的弯矩.因此,有必要研究施工顺序对邻近既有隧道的影响.本研究采用三维有限元分析方法,研究了施工顺序对垂直交叉隧道的影响.数值分析采用砂土的亚塑性本构模型,考虑了土体的小应变刚度.此外,将计算结果与只模拟体积损失(即不考虑重量损失的影响)的情况进行比较,以证明质量损失对不同施工顺序的显著影响.对既有隧道的地面沉降、变形和位移、弯矩和轴向力的影响进行了研究.同时对土的应力传递机理进行了分析,并将其应用于土的力学行为研究.
1数值模型
1.1有限元网格和边界条件
图1和图2显示了针对工况S1和S2的平面图和正视图.工况S1指在既有隧道上方新建隧道的情况,而工况S2指在既有隧道下方新建隧道的情况.新建和既有隧道均为盾构隧道,长度和直径分别为100 m和5 m,隧道衬砌厚度为0.2 m.根据《公路隧道设计规范》(JTG D70-2014),本研究假设隧道衬砌厚度为0.2 m.矿柱宽径比P/D为1.0,其中矿柱宽度定义为两隧道衬砌之间的最短距离.假设C/D为8.5,即距离地面42.5 m.利用有限元程序ABAQUS[16]对既有隧道上方和下方隧道开挖进行了模拟.
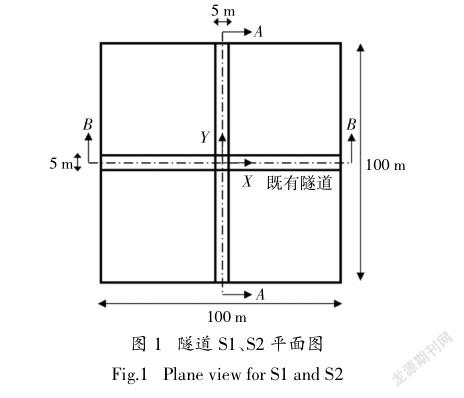
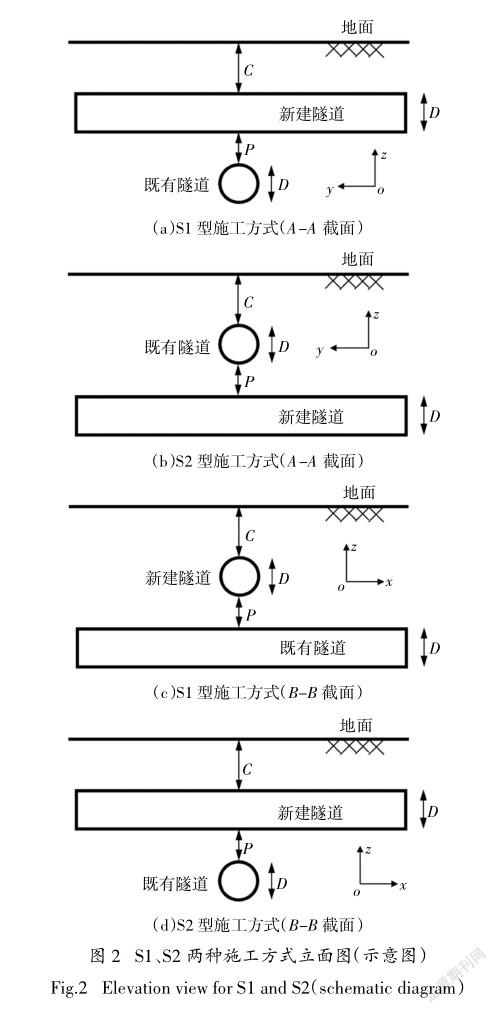
图3为工况S1的三维有限元网格,新隧道轴线位于距地面45 m处,距既有隧道轴线10 m处.工况S2的网格与S1相似,新隧道和既有隧道的位置与S1正好相反.此外,还分析了另外两种无既有隧道工况(对应S1和S2),以比较工况S1、S2的地表沉降槽情况.上述6种工况参数见表1.网格尺寸为100 m(长)×100 m(宽)×100 m(高),由22 556个元素和26 341个节点组成.采用四节点壳单元对隧道衬砌进行建模,采用八节点实体单元对土体进行建模.边界条件为底部及四个垂直面固定,从而限制底部和四个垂直面在任何方向的运动.


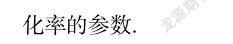
通过ABAQUS的用户材料子程序(User-defined Material Mechanical Behavior,简称UMAT)接口程序对亚塑性模型进行数值实现.本研究中采用Masin[19]开发的UMAT程序.该程序利用与有限元相结合的基于矩阵广义逆一致性切向模量矩阵,形成了通过UMAT接口实现亚塑性模型的数值方案.
本研究中,假设土体为丰浦砂,表2为丰浦砂亚塑性模型参数[20].混凝土隧道衬砌采用线弹性材料.考虑到衬砌接头对衬砌结构刚度的影响,将衬砌管片结构刚度折减0.15,杨氏模量为30 GPa(折减后),泊松比为0.25[21].隧道衬砌的有效单位重量为25 kN/m3[5].

1.3数值模拟方案
如前述表1所示,共分析了6种工况.首先进行了S1和S2两种不同施工顺序的分析,研究了新建隧道对地面和既有隧道的影响.为了研究既有隧道在新建隧道开挖下对地面沉降的影响,增加了仅有隧道开挖的工况(无既有隧道,对应于S1和S2).在只模拟体积损失的情况下进行了另外两种工况,以证明建模质量损失对不同施工顺序的显著影响,即在隧道衬砌周围开挖只模拟2%的体积损失,而没有开挖隧道衬砌内部的土.根据北京、上海、武汉、深圳等地盾构隧道施工引起的地表损失率数据,对71组数據进行统计分析.结果表明,地表损失率在0.2% ~ 3.01%之间[22].因此,本研究假设2%的体积损失是合理的.本研究采用的模拟隧道开挖的数值模型已被广泛应用,并得到了前人研究的验证[23-25].
图5为隧道开挖过程.在盾构掘进过程中,开挖面支护力沿深度线性变化,大小与侧向土压力相同[26],注浆压力为0.2 MPa[27].新建隧道(长100 m)分为80段,每段挖土1.25 m.为了既能反映盾构推进过程及其对既有隧道的影响,又能满足计算量要求,避免尺寸效应及边界带来的计算误差,新建隧道开挖时首先会挖去8段,共计挖土10 m.隧道开挖是通过移除位于开挖区域的土体来模拟的,即通过使土体单元失活来开挖隧道衬砌内部和衬砌周围的土体.每一个开挖步包含两个分析步:第一步为应力释放,即刚度折减过程,在刚度折减的同时,在开挖面处施加支护力.第二步开挖土体然后生成衬砌,土体与衬砌单元的接触设为绑定接触(*interaction,tie adjusted sur-face).绑定接触可以实现两个面之间没有连接关系,从这个分析步开始才绑定在一起.在只考虑体积损失的情况下,仅在衬砌周围开挖土体.衬砌会在重力作用与土层接触,进行应力传递.如图5所示,土体与隧道外径之间的间隙相当于2%的体积损失.这样简化了隧道衬砌周围2%体积损失的位移控制方法.模拟重量损失时,将隧道内部的土体单元全部失活.隧道开挖过程可视为盾构掘进.这种建模技术可以模拟隧道施工过程中的重量损失和体积损失.在每个掘进阶段,隧道工作面不允许发生水平位移.

2结果分析
2.1地表沉降
图6为开挖结束时沿B-B段计算出的地表横向沉降槽.其中,图6的实测值是Ng等[24]在60g条件下离心机模型试验测得的结果,试验中新建隧道在既有隧道下方(C/D = 2;P/D = 0.5).对于双隧道的工况(S1和S2),工况S1的最大地表沉降大于工况S2,其中S1和S2的最大地表沉降分别为6.6 mm和6.2 mm.这是因为S1的新隧道C/D比S2的小.对比工况S2和实测值,沉降量随中心线偏移量的变化均呈现中间大两头小的规律,最大地表沉降相差4 mm.这是由于Ng等[24]的试验条件P/D = 0.5,工况S2的P/D = 1,根据Ng等[14]论文的结果,P/D较小时,既有隧道中心线处的沉降较大.因此,模型预测结果较为合理.图中S1-gf和S2-gf为无既有隧道工况,地表最大沉降量(即S1-gf和S2-gf)分别大于相应的双隧道条件(即S1和S2).这是由于现有隧道的存在使土体变硬,导致S1和S2两种情况下最大地表沉降降低了约14%.

另一方面,仅有体积损失工况(S1-vl和S2-vl)的地表沉降均小于双隧道和无既有隧道的沉降. S1-vl和S2-vl最大地表沉降分别为5.8 mm和5.4 mm.也就是说,S1-vl和S2-vl的地表最大沉降量分别比S1和S2小12%和13%.可以解释为隧道衬砌内土体质量的去除引起了新隧道周围总应力的变化.与只考虑体积损失影响而不考虑质量损失影响的S1-vl和S2-vl相比,S1和S2的新隧道周围出现较大的应力释放.因此,地表沉降小于S1和S2两种情况.
2.2隧道纵向沉降
图7为既有隧道沿B-B截面(见图1)的纵向沉降分布,不同推进阶段的纵向沉降量通过y/D比值表示. y/D代表隧道掌子面与既有隧道中心线(B-B截面)的距离与隧道直径的比值.随着y/D比值的增加,工况S1和S1-vl既有隧道的轴线部分向上位移(即隆起),工况S2和S2-vl向下位移(即沉降).這是因为隧道开挖会减少既有隧道的应力,导致既有隧道向新建隧道移动. S1处既有隧道最大沉降量为9 mm,S2处最大沉降量为16 mm. S1和S2沉降差分别为11.6 mm和11.8 mm. S1和S2差异沉降分别相当于1∶2 800和1∶2 400的梯度. S2沉降差和梯度略大于S1,这是由于应力释放的作用更大. S1-vl和S2-vl的差异沉降量小于S1和S2. S1-vl和S2-vl的差异沉降分别比S1和S2小54%和53%.由于没有减少衬砌内土体质量,导致S1-vl和S2-vl的应力释放效果小于S1和S2.
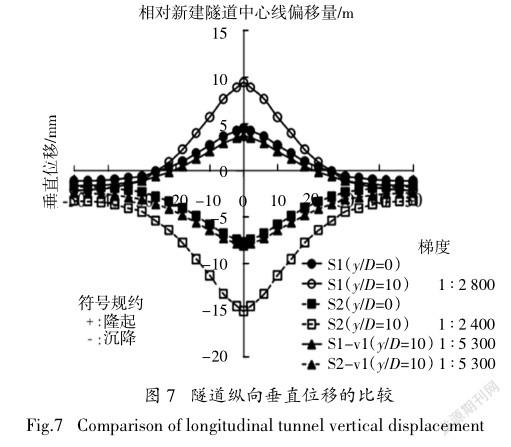
图8为在工况S2中不同推进阶段(y/D表示)竖向位移U3的云图.为了便于观察,只截取了靠近隧道的局部区域.随着新建隧道的不断推进,工况S2既有隧道及周围土体的竖向位移不断增大,新建隧道下部结构、土体均产生不同程度的“上浮”,最大值位于隧道结构的临空面.
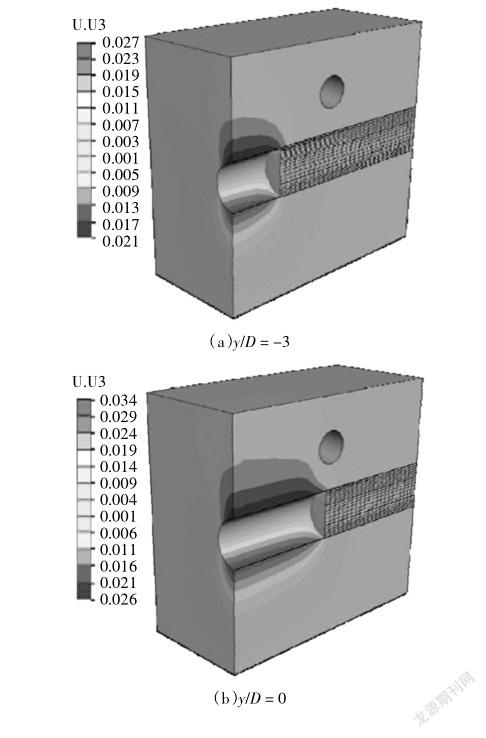

2.3既有隧道的位移和变形
图9为既有隧道在A-A截面不同推进阶段(y/ D表示)的位移和变形形态.随着y/D比值的增加,工况S1既有隧道发生了向上位移(即隆起),工况S2既有隧道发生了向下位移(即沉降).这是因为隧道开挖会减小既有隧道的应力,从而导致既有隧道向新建隧道移动. S1和S2工况下,既有隧道在开挖结束时的最大向上和向下垂直位移分别约为9.4 mm和15.0 mm(即在y/D = 10处).工况S2的最大向下垂直位移比S1最大向上位移大60%.这是因为工况S1中上覆土体压力阻碍了既有隧道的位移,导致既有隧道向上位移较小(见图7).另一方面,工况S2的向下位移是由仰拱处的应力降低和既有隧道上方土体压力共同作用的结果.当隧道掌子面y/D = -1时,既有隧道向新隧道掌子面位移,当隧道掌子面通过监测断面后,横向水平位移回到原来的位置.在隧道施工过程中,由于应力释放的作用,既有隧道在掘进过程中往往向开挖掌子面y方向移动.
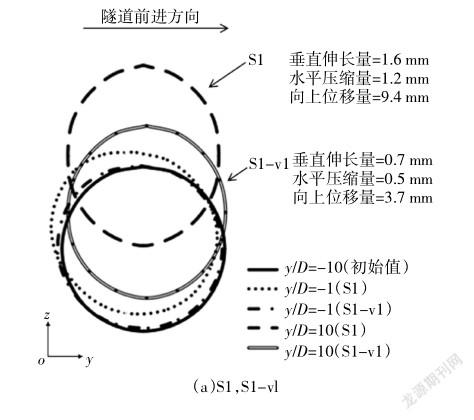

由于应力释放作用,随着y/D的增大,水平直径减小(即压缩),垂直直径增大(即拉长).工况S1的变形在伸长和压缩两方面均略小于S2,S2既有隧道的垂直延伸和水平压缩分别比S1大6%和9%. S1和S2工况下既有隧道的竖向伸长主要是隧道顶部衬砌变形引起的.通过考虑隧道周围的正应力变化导致隧道衬砌产生弯矩,进一步验证了这一点.在开挖完成时(即y/D = 10时),S1和S2的垂直伸长量分别比水平压缩量大约33%和54%.另一方面,S1-vl和S2-vl两种情况下,各既有隧道的竖向位移和变形均小于S1和S2两种情况. S1-vl组和S2-vl组的上下垂直位移分别比S1组和S2组小61%和47%.这是由于与S1和S2相比,S1-vl和S2-vl没有减少衬砌内土体质量,导致应力释放更小.与S1和S2类似,S2-vl的向下垂直位移大于S1-vl的向上位移,这是因为减重的影响会引起新隧道周围总应力的变化.随后,当新隧道穿越既有隧道时,既有隧道会因减重而产生额外的应力降低. S1-vl和S2-vl隧道变形分别小于S1和S2的变形,S1-vl和S2-vl的垂直伸长量分别比S1和S2小56%和59%.与S1和S2相似,S2-vl的变形大于S1-vl.这是因为S2-vl的拱顶最大弯矩远大于S1-vl.
2.4既有隧道的弯矩
图10(a)和10(b)为开挖完成时既有隧道衬砌沿A-A截面的横向弯矩分布.正弯矩表示既有隧道向外变形,负弯矩表示现有隧道向内变形.

如图10(a)和10(b)所示,S1和S1-vl最大横向弯矩发生在拱顶,S2和S2-vl最大横向弯矩发生在拱底,在S1、S2、S1-vl和S2-vl四种工况,最小弯矩均出现在起拱线上.工况S1最大和最小横向弯矩略小于工况S2.

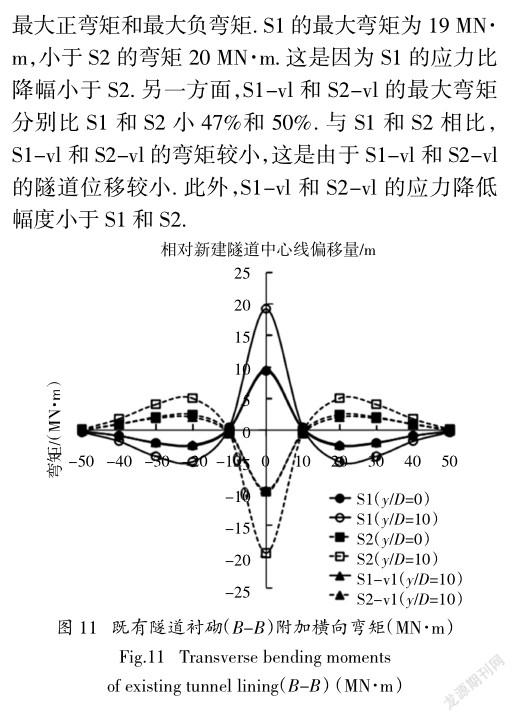
2.5既有隧道衬砌轴向力
图12(a)(b)分别为S1、S1-vl、S2、S2-vl开挖完成时既有隧道衬砌沿A-A段的环向力和纵向轴向力.由图12(a)可知,对于工况S1和S2,最大的环向力都在拱脚处,最小的环向力在拱顶和拱脚.最大和最小轴力分别为372 kN/m和197 kN/m.对于工况S1来说,拱脚以上的环向力大于拱脚以下的环向力,从而导致既有隧道的隆起.相反,在工况S2中,拱脚以下的环向力大于拱脚以上的环向力,导致既有隧道的沉降. S1-vl和S2-vl的环向力分别小于S1和S2.这是由于S1-vl和S2-vl的隧道变形分别小于S1和S2(见图9),且S1-vl和S2-vl的应力降低量分别小于S1和S2(见图13).
从图12(b)可看出,最大纵向轴力分别出现在工况S1的拱顶处和工况S2的拱底处,而最小轴力出现在工况S1的拱底处和工况S2的拱顶处.这是由于S1拱顶和S2拱底附近的应力释放.在S1和S2两种工况下,襯砌所承受的最大轴力分别为579 kN/ m和584 kN/m. S1-vl和S2-vl的轴力大小分别小于S1和S2.这是由于S1-vl和S2-vl的隧道变形要小于S1和S2(见图9),且S1-vl和S2-vl的隧道应力降低量小于S1和S2.
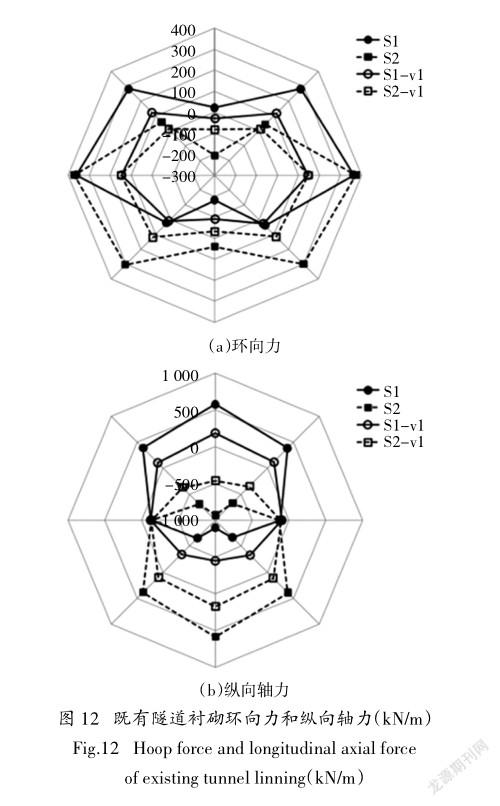
2.6应力传递机制
图13为新建隧道沿A-A截面推进的不同阶段既有隧道周围土体归一化纵向、横向、竖直应力比σxx/σv、σyy/σv、σzz/σv.其中,σxx为沿既有隧道轴线方向(x方向)的正应力,σyy为沿新建隧道轴线方向(y方向)的正应力,σzz为竖直方向(z方向)的正应力,σv为新建隧道未开挖时对应位置的竖向有效应力. S1和S2分别选择拱顶、拱肩、拱脚和拱底作为监测点.
图13(a)为归一化应力比纵向方向上,当隧道掌子面达到y/D=-3位置时,σxx/σv略有增加.当隧道掌子面接近既有隧道的中线时,S1拱顶、拱肩应力比和S2拱脚、拱底应力比均显著降低.当掌子面达到y/D=1.5时,应力比达到最小值.当掌子面达到y/D=2时,S1拱顶处应力比和S2拱底处应力比略有增加.
在图13(b)中,当掌子面达到y/D = -3时,隧道的横向应力发生了明显的变化.当y/D = -0.5时,工况S1拱肩和S2的拱脚处横向应力比σyy/σv大大提高,当隧道开挖面到y/D = 0.5时,达到最大. S1拱肩和S2拱脚处应力比的增加和S1拱顶和S2拱底处应力比的减少表明,S1拱顶和S2拱底处的应力传递至S1拱肩和S2拱脚处.

3结论
本文基于砂土亚塑性本构模型采用有限元分析方法进行了不同施工顺序的垂直交叉隧道数值试验,研究了施工顺序对垂直交叉隧道的影响及既有隧道附近土体的应力传递机制,得出以下结论:
1)与下穿工况相比,上穿工况的地表沉降较大,但影响范围较小.与无既有隧道工况相比,有既有隧道工况最大沉降量降低14%.下穿工况中新建隧道对既有隧道的影响在位移和变形上都比上穿工况更为显著.
2)上穿工況和下穿工况的最大弯矩分别出现在拱顶和拱底处,而最小弯矩出现在拱脚处.下穿工况中既有隧道的最大弯矩和最小弯矩的大小均大于上穿工况.
3)当新建隧道掌子面接近既有隧道中心线时,上穿工况的拱顶横向和纵向应力传递至拱肩,下穿工况的拱底横向和纵向应力传递至拱脚处.
4)有既有隧道工况下,当掌子面距离既有隧道中心线后方3D和前方6D之间时,应力释放对既有隧道的影响显著.
5)只考虑体积损失的工况的地表沉降小于同时考虑体积和质量损失的工况,而且既有隧道的竖向位移和变形、附加弯矩、轴向力均更小.
在垂直交叉隧道施工中,应充分考虑施工顺序对地表沉降、既有隧道的影响.本研究的局限性主要包括两个方面:首先,模拟中采用的土体本构模型不考虑土体的小应变(0.001% ~ 1%)刚度.其次,干砂隧道衬砌的力学参数缺乏相应的工程背景.为了辅助工程设计,进一步的数值研究应结合具体的实际工程或模型试验.
参考文献
[1]COOPER M L,CHAPMAN D N,ROGERS C D F,et al.Movements in the piccadilly line tunnels due to the heathrow express construc-tion[J].Géotechnique,2002,52(4):243—257.
[2]MAIR R J,TAYOR R N,BURLAND J B. Prediction of ground movements and assessment of risk of building damage due to bored tunneling[C]// Proceedings for Geotechnical Aspects of Under-groundConstructioninSoftGround.London:Universityof Southampton Press,1996:713—718.
[3]LEE Y J,YOO C S.Behavior of a bored tunnel adjacent to a line of loaded piles[J].Tunneling and Underground Space Technology,2006,21(3/4):370.
[4]WW NG C,LEE K M,KW TANG D.Three-dimensional numerical investigations of new Austrian tunneling method(NATM)twin tun-nel interactions[J].Canadian Geotechnical Journal,2004,41(3):523—539.
[5]方勇,汪辉武,郭建宁,等.下穿黄河盾构隧道管片衬砌结构受力特征模型试验[J].湖南大学学报(自然科学版),2017,44(5):132—142. FANG Y,WANG H W,GUO J N,et al.Model test study on the me-chanical characteristics of segment linings for the shield tunnel un-dercrossing the Yellow River[J].Journal of Hunan University(Nat-ural Sciences),2017,44(5):132—142.(In Chinese)
[6]LIU H L,LI P,LIU J Y.Numerical investigation of underlying tun-nel heave during a new tunnel construction[J].Tunneling and Un-derground Space Technology,2011,26(2):276—283.
[7]NEMATOLLAHI M,DIAS D.Three-dimensional numerical simula-tion of pile-twin tunnels interaction - Case of the Shiraz subway line[J].Tunneling and Underground Space Technology,2019,86:75—88.
[8]张运强,曹文贵,邢静康,等.动力扰动下既有隧道的动态响应及衬砌影响分析[J].湖南大学学报(自然科学版),2018,45(S1):138—143. ZHANG Y Q,CAO W G,XING J K,et al.Dynamic response and lining impact of existing tunnel analysis under dynamic perturbation[J].Journal of Hunan University(Natural Sciences),2018,45(S1):138—143.(In Chinese)
[9]SHIVAEI S,HATAF N,PIRASTEHFAR K.3D numerical investi-gation of the coupled interaction behavior between mechanized twin tunnels and groundwater - A case study:Shiraz metro line 2[J]. Tunneling and Underground Space Technology,2020,103:103458.
[10]WU W,BAUER E.A simple hypoplastic constitutive model for sand[J].International Journal for Numerical and Analytical Methods in Geomechanics,1994,18(12):833—862.
[11]WANG S,WU W,PENG C,et al.Numerical integration and FE im-plementation of a hypoplastic constitutive model[J].Acta Geotech-nica,2018,13(6):1265—1281.
[12]KIM S H,BURD H J,MILLIGAN G W E.Model testing of closely spaced tunnels in clay[J].Géotechnique,1998,48(3):375—388.
[13]LIU H Y,SMALL J C,CARTER J P,et al.Effects of tunnelling on existing support systems of perpendicularly crossing tunnels[J]. Computers and Geotechnics,2009,36(5):880—894.
[14]NG C W W,BOONYARAK T,MASIN D.Effects of pillar depth and shielding on the interaction of crossing multitunnels[J].Journal of Geotechnical and Geoenvironmental Engineering,2015,141(6):04015021.
[15]WANG R,NG C W W,BOONYARAK T. Effect of an existing tunnelshape on crossing tunnels’ interaction[J]. Geotechnical Special Publication,2017,277:505—514.
[16]HIBBITT K. Abaqus user’s manual[M]. version 6.14. Rhode Is-land,USA:Hibbitt Karlson and Sorensen Inc,2016:25—78.
[17]VON WOLFFERSDORFF P A.A hypoplastic relation for granular materials with a predefined limit state surface[J].Mechanics of Co-hesive-Frictional Materials,1996,1(3):251—271.
[18]NIEMUNIS A,HERLE I.Hypoplastic model for cohesionless soils with elastic strain range[J].Mechanics of Cohesive-Frictional Ma-terials,1997,2(4):279—299.
[19]MASIN D.Modelling of soil behaviour with hypoplasticity[M]. Cham:Springer Nature Switzerland AG,2019:89—101.
[20]HONG Y,SOOMRO M A,NG C W W.Settlement and load transfer mechanism of pile group due to side-by-side twin tunnelling[J]. Computers and Geotechnics,2015,64:105—119.
[21]TANG K W D. Numerical studies of multiple NATM tunnel interac-tion in soft ground[D]. Hong Kong:Hong Kong University of Sci-ence and Technology,2001:34—47.
[22]魏纲.盾构隧道施工引起的土体损失率取值及分布研究[J].岩土工程学报,2010,32(9):1354—1361. WEI G.Selection and distribution of ground loss ratio induced by shield tunnel construction[J].Chinese Journal of Geotechnical En-gineering,2010,32(9):1354—1361.(In Chinese)
[23]李强,曾德顺.盾构施工中垂直交叉隧道变形的三维有限元分析[J].岩土力学,2001,22(3):334—338. LI Q,ZENG D S.3D FEM deformation analysis with the new tunnel perpendicularly crossing under the old one[J].Rock and Soil Me-chanics,2001,22(3):334—338.(In Chinese)
[24]NG C W W,BOONYARAK T,MASIN D.Three-dimensional cen-trifuge and numerical modeling of the interaction between perpen-dicularly crossing tunnels[J].Canadian Geotechnical Journal,2013,50(9):935—946.
[25]BOONYARAK T,NG C W W.Effects of construction sequence and cover depth on crossing-tunnel interaction[J].Canadian Geotechni-cal Journal,2015,52(7):851—867.
[26]杜勝,钟俊辉,尹培林.福州砂土地层土压平衡盾构隧道掘进参数和地表沉降特性分析[J].现代隧道技术,2019,56(S2):379—385. DU S,ZHONG J H,YIN P L.Analysis of driving parameters and surface subsidence characteristics of the EPB shield tunnel in Fuzhou sand soil[J].Modern Tunnelling Technology,2019,56(S2):379—385.(In Chinese)
[27]ZHAO K,BONINI M,DEBERNARDI D,et al.Computational mod-elling of the mechanised excavation of deep tunnels in weak rock[J].Computers and Geotechnics,2015,66:158—171.
