基于GPU的车辆-轨道-地基土耦合系统3D随机振动并行计算方法
2021-02-09朱志辉夏禹涛王力东刘禹兵
朱志辉 夏禹涛 王力东 刘禹兵
摘要:針对轨道不平顺随机特征导致车辆-轨道-地基土耦合系统随机分析计算效率低的问题,采用虚拟激励法降低大样本分析的计算量;针对耦合系统等效刚度矩阵的稀疏特性,采用行压缩(Compressed Sparse Row,CSR)格式存储大型稀疏矩阵,采用预处理共轭梯度法(Preconditioned Conjugate Gradient,PCG)求解对称正定的等效静力平衡方程,最后通过MAT-LAB-CUDA(Compute Unified Device Architecture)混合平台开发基于GPU的并行计算程序.数值算例表明:基于MATLAB-CUDA混合平台求解等效静力平衡方程的效率是串行多点同步算法的86.13倍,大大缩短了随机振动分析的总计算时间,且内存占用小、易于在个人计算机上实施;采用PCG法求解车辆-轨道-地基土耦合系统形成的大型稀疏线性方程组时,建议以加速度指标作为迭代收敛精度的控制指标;可通过选取适当的迭代收敛精度,以达到计算精度和计算效率的平衡.
关键词:随机振动;GPU并行计算;3D有限元法;虚拟激励法;车辆-轨道-地基土耦合模型
中图分类号:U211.3;TP399文献标志码:A
基金项目:国家自然科学基金资助项目(51678576,52078498),National Natural Science Foundation of China(51678576,52078498);国家重点研发计划项目(2017YFB1201204),National Key R&D Program of China(2017YFB1201204)
A Parallel Computing Method for Three-dimensional Random Vibration of Train-track-soil Dynamic Interaction Based on GPU
ZHU Zhihui1,2,XIA Yutao1,WANG Lidong3,LIU Yubing1
(1. School of Civil Engineering,Central South University,Changsha 410075,China;2. National Engineering Laboratory for High Speed Railway Construction,Central South University,Changsha 410075,China;3. School of Civil Engineering,Changsha University of Science & Technology,Changsha 410114,China)
Abstract:Aiming at the issue of low efficiency in the random analysis and calculation of train-track-soil cou-pled system due to the random characteristics of track irregularity,the pseudo-excitation method(PEM)is used to re-duce the computing cost of large samples. Considering the sparsity of equivalent stiffness matrix of train-track-soil coupling system,the large-scale sparse matrix was stored in Compressed Sparse Row(CSR)format. The symmetric positive definite equation of equivalent static equilibrium is solved by the preconditioned conjugate gradient(PCG)method,and the parallel program is developed by the MATLAB-CUDA(Compute Unified Device Architecture)hy-brid platform. The numerical example shows that the efficiency of solving equivalent static equilibrium equation based on MATLAB-CUDA hybrid platform is 86.13 times that of the multi-point synchronization algorithm,which greatly reduces the total calculation time of the random vibration analysis,and the memory usage is small and it is easy to im-plement on a personal computer. When using PCG method to solve the large sparse linear equations of vehicle-trackfoundation soil coupling system,it is suggested to take the acceleration as the control index of convergence accuracy of iteration. By choosing the appropriate convergence accuracy of iteration,the balance of calculation accuracy and effi-ciency is achieved.
Key words:random vibration;GPU parallel computing;three dimensional finite element method;pseudo-exci-tation method;train-track-soil couple model
随着列车速度、轴重、路网密度和行车密度的提高,铁路运输引起的振动对周围环境的影响问题日渐突出.计算机性能的不断提升使得有限元法[1-2]、有限元/无限元法[3]、边界元法[4]等数值计算方法能够广泛用于研究车辆引起的周围环境振动问题;根据所建立的模型维度可将数值模型分为2D模型[5]、2.5D模型[3]和3D模型[2].与3D模型相比,2D和2.5D模型假设轨道-地基土模型的几何形状和材料特性沿车辆运动方向保持不变或周期性变化,计算中只需建立线路的横截面模型,具有计算效率高的优点.但车致环境振动实质上是3D空间上的工程问题,3D模型可以考虑地基土的不连续性及与附近结构的耦合[6],因此仍具有不可替代的普适性.
同时,轨道不平顺的随机性导致轮轨相互作用力具有随机性,移动车辆引起的任何特定地面位置的振动均是一个非平稳的随机过程[7].采用蒙特卡罗法等常规方法分析随机响应时由于样本过多导致计算效率较低.针对随机振动计算效率低的问题,林家浩等提出了高效的虚拟激励法,该法已被广泛地用于分析平稳或非平稳随机激励下线性系统的随机响应[8].虚拟激励法将平稳随机振动分析转化为谐响应分析,将非平稳随机振动分析转化为可用数值积分方法求解的确定性瞬态分析,与蒙特卡罗方法相比,其计算效率提高了1~2个数量级[9-10]. Wang等[2]采用虚拟激励法分析车辆-轨道-地基土的随机振动,基于填充元优化与多波前法提出了一种求解大型稀疏线性方程组的多点同步算法,进一步节省了计算时间.这些方法大部分都在传统CPU串行平台上开展并实施.由于车辆-轨道-地基土耦合系统3D有限元模型的自由度数量庞大,且使用虚拟激励法进行随机振动分析时仍需求解一系列大型稀疏线性方程组,因此计算效率低仍然是基于3D模型开展随机振动分析面临的主要问题.
近年来,并行计算等高性能计算技术的发展为大规模的工程计算问题提供了高效的解决方案.在随机振动领域,聂旭涛等[11]结合有限元EBE并行策略和虚拟激励法实现了结构随机振动的并行计算,其中通过消息传递接口(MPI)实现多CPU节点间的通讯,并证明了该算法的准确性和高效性.张健[12]利用虚拟激励法中每个频点的随机响应计算相互独立的特点,采用包含8个CPU的工作站实现虚拟激励法的并行计算,每个CPU平均分配各频点的计算任务,结果表明计算加速比几乎与CPU数目成线性关系.这些方法通过CPU集群实现程序的并行化加速,但是CPU集群平台搭建与维护的成本较高.随着GPU通用计算的发展,CUDA等统一计算架构和编程环境的出现为GPU并行计算提供了易用的编程接口.相对于传统的CPU串行计算,GPU的浮点计算能力更强、内存带宽更大,具有低功耗和高性价比的特点,因此越来越广泛地应用于科学研究和工程計算中.陈曦等[13]通过使用CPU-GPU混合计算构架加速了预处理Krylov子空间迭代法,从而提升了岩土工程有限元分析的效率;蔡勇等[14]基于GPU并行计算平台CUDA,使用多重网格法加快Jacobi迭代的收敛速度,在采用GTX 460显卡的个人计算机上有效提高了大规模壳结构有限元分析的效率.
综上所述,针对轨道不平顺随机特征导致车辆-轨道-地基土耦合系统随机分析计算效率低的问题,采用虚拟激励法降低大样本分析的计算量;针对车辆-轨道-地基土耦合系统等效刚度矩阵的稀疏特性,采用行压缩格式存储大型稀疏矩阵,采用预处理共轭梯度法并行求解等效静力平衡方程,最后通过MATLAB-CUDA混合平台开发并行计算程序.通过数值算例验证了该并行计算方法的高效性,并给出了使用该法进行车致场地振动分析时迭代收敛精度选取的建议.
1车辆-轨道-地基土耦合系统的3D随机振动分析模型
1.1车辆-轨道-地基土耦合振动模型
车辆-无砟轨道-路堤-地基土系统可分为车辆子系统和轨道-地基土子系统,两个子系统通过轮轨相互作用耦合为一个整体,如图1所示.




2基于GPU的耦合时变系统随机振动并行求解方法
使用虚拟激励法分析随机振动时,仍需求解一系列形如式(17)的等效静力平衡方程,该步骤巨大的计算耗时是3D模型难以广泛用于随机振动分析的重要原因.根据并行系统的安姆达尔加速定律[17](Amdahl’s law),对该步骤进行并行化加速能获得更大的加速比.
2.1基于GPU的统一计算架构
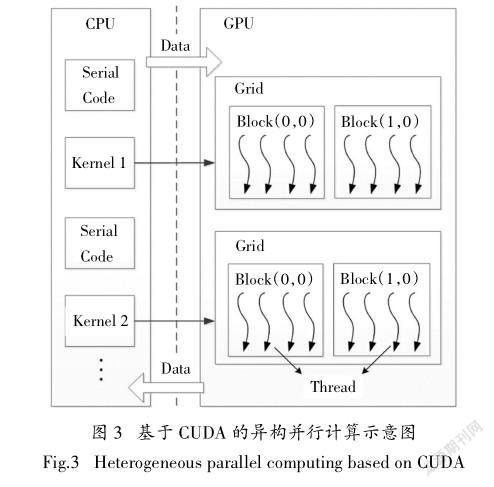
CUDA(Compute Unified Device Architecture)平台是NVIDIA公司于2006年提出的GPU通用计算编程接口,它大大简化了通用计算向GPU上移植的难度,缩短了程序开发的周期. CUDA称CPU为主机(Host),称GPU为设备(Device),使用GPU设备进行并行计算主要包括3个步骤:①在主机端与设备端分别分配计算数据所需的内存,将数据从主机端复制到设备端;②由设备端执行并行计算程序;③将计算结果数据从设备端复制到主机端.
基于CUDA的并行计算是建立在CPU和GPU协同工作的异构并行计算.如图3所示,其中CPU主要负责程序中逻辑流程的控制及执行部分串行代码,GPU负责执行大规模数据的并行计算部分.每个GPU设备由若干个流处理器簇(SM)组成,每个SM配备多个流处理器(SP),在GPU上执行的并行程序称为核函数(Kernel),其中规定了线程(Thread)的组织和内存的管理.线程是并行计算的基本构建块,CUDA的编程模型将线程组合形成了线程束(Warp)、线程块(Block)以及线程网格(Grid). GPU多线程的计算构架适合于大型3D有限元模型分析中涉及的大规模矩阵运算等操作.
2.2等效静力平衡方程的并行求解
耦合系统随机振动分析中的等效靜力平衡方程为大型稀疏线性方程组.线性方程组的解法一般分为直接法和迭代法,直接法经过有限步计算可得到方程组的精确解,但矩阵分解产生的大量填充元导致直接法的存储量较大.迭代法可利用矩阵稀疏的特性,因此所需的内存占用小且易于编程实现,被广泛用于大型稀疏线性方程组的求解,但需考虑计算精度和收敛速度的问题,一般来说,迭代循环的次数和计算时间随收敛精度取值的减小而增大.考虑到GPU内存的限制和并行编程的难度,本文选用迭代法求解等效静力平衡方程.
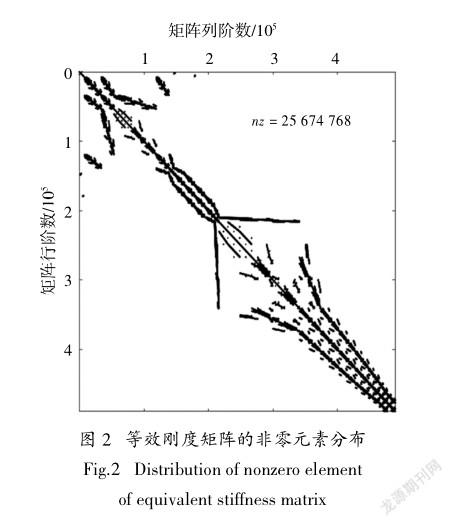
3D有限元方法形成的大型稀疏矩阵中含有大量不参与矩阵运算的零元素,图2所示矩阵的稀疏度达到0.107‰,采用压缩存储的方式存储稀疏矩阵可大大减少迭代求解时的内存占用、避免额外的计算开销.为了满足3D有限元法生成的无规则的系数矩阵,本文采用对矩阵结构无要求且适合并行编程的CSR格式[18]存储等效刚度矩阵K,该法对稀疏矩阵进行逐行压缩处理,只存储非零元素及其位置索引.对于一个包含nz个非零元素的n×n维稀疏矩阵,分别使用三个一维数组存储矩阵信息,如图4所示.其中,Val数组含nz个元素,用于存储所有非零元素的值;RowPtr数组含(n+1)个元素,用于存储矩阵每行首个非零元素在数组Val中的位置;ColInd数组含nz个元素,用于存储每个非零元素所在列位置.程序中,Val数组的数据类型设为双精度浮点型(double),RowPtr和ColInd数组的数据类型设为整型(int).

针对图2所示的系数矩阵对称正定的特征,采用Krylov子空间迭代法中的共轭梯度法进行求解.为了改善迭代求解的收敛性能,采用矩阵预处理技术减少系数矩阵条件数、改善其病态特征从而加快收敛速度.常用的预处理技术包括Jacobi预处理、不完全Cholesky分解预处理(IC)、多项式预处理和对称超松弛预处理(SSOR)[19]等.本文采用的Jacobi预处理是一种简单易行的预处理方法,能在不增加额外内存需求、通信开销小的前提下达到较好的收敛性能,从而提高计算效率.对于线性方程组Ax = b,取系数矩阵的对角项形成对角预处理矩阵,如(18)式所示:
M = diag(A)(18)
采用预处理技术的共轭梯度法称为预处理共轭梯度法(PreconditionedConjugateGradientMethod,PCG).
PCG法将等效静力平衡方程的求解转化为矩阵和向量间的运算,其中主要包括稀疏矩阵向量乘、向量更新和向量内积运算,它们都适合于利用GPU进行的细粒度并行计算.基于CUDA的并行PCG法计算流程如表1所示,其中Jacobi预处理通过自编核函数实现,其余的矩阵向量运算通过调用CUBLAS和CUSPARSE函数库实现.
2.3耦合时变系统随机振动并行计算流程


通过MATLAB-CUDA混合平台开发了计算程序,其中CPU端的程序在擅长矩阵数值运算的MATLAB平台上编制,通过调用CUDA程序在GPU端实现并行PCG法求解等效静力平衡方程.其中,采用cudaMemcpy函数实现CPU和GPU间的数据传输,通过NVIDIA Visual Profiler软件进行CUDA程序的耗时分析.结果表明:对于本文研究对象,每一时间步内CPU和GPU间的数据传输时间小于0.5 s,占该步总计算时间的1%以内,因此数据传输对计算效率的影响较小,该并行计算流程适合本文耦合时变系统的随机动力分析.
MATLAB中调用CUDA并行程序的步骤如下:利用nvcc编译器将CUDA代码(.cu)编译成目标文件(.obj),使用mex命令编译C++代码(.cpp)并将其链接到CUDA目标文件(.obj),最终得到可执行的动态链接库文件(.mexw64).其中,CUDA代码(.cu)完成了主机端和设备端间的数据传输和PCG法的并行求解流程. C++代码(.cpp)中定义了被MATLAB调用的外部子程序的入口地址、MATLAB系统和子程序间传递的参数.
3数值算例
3.1有限元模型和计算参数
以京沪高铁某路基段试验场地为例,建立了如图6所示的有限元模型,模型参数通过现场实测获得[20].为控制有限元模型的尺寸,除地表外的其他五个边界面采用3D黏弹性人工边界[21]模拟半无限域场地.地基土参数、有限元模型横截面几何参数、有限元模型单元尺寸及车辆参数,参考文献[2]中数据.整个3D有限元模型由210 686个单元、193 135个节点和542 002个自由度组成,采用CSR格式存储后的等效刚度矩阵所占内存仅为296.7 MB.

本文算例仅考虑单线行车,车辆选取8车编组的CRH3型高速列车组,车速设为316 km/h.选取德国低干扰高低不平顺轨道谱作为随机激励,如图7所示取其空间频域范围为0.0125×2π~1×2π,并在该范围内等间距离散为100个频点(即m = 100).轨道-地基土系统有限元模型采用瑞利阻尼,阻尼比取0.05.时间积分步长为0.002 s,当考虑车辆的运行时间为4 s时,总时间步为2 000.

3.2计算精度分析
为了验证本文方法的计算精度,考虑到PCG法中迭代收敛精度ε对车辆-轨道-地基土耦合系統3D随机振动计算精度的影响,分别取ε为10-7和10-6进行计算,并与文献[2]中串行的ANSYS求解所得结果进行对比.选取了如图8所示的A、B、C和D四个采样点,它们与轨道中心线的距离分别是0 m、7.5 m、20 m和40 m.本文所采用的计算平台参数如表2所示.图9和图10分别给出了四个采样点竖向速度和竖向加速度标准差的ANSYS求解和不同精度下本文方法计算的结果.



结果表明:
1)当收敛精度ε取10-7时,本文方法所得四个采样点的计算结果与ANSYS所得结果均吻合良好,具有较高的精度.
2)当收敛精度ε取10-6时,A点的计算结果吻合良好;3 s后离轨道中心线较远的B、C和D点的竖向速度标准差轻微偏离,竖向加速度标准差严重偏离.经过分析,造成该现象的主要原因包括:①每一步的计算精度下降导致PCG算法的截断误差随着时间步的积累效应逐渐显著.②3 s之后振动响应的数值减小,同时距离轨道中心线越远的振动响应数值越小,此时计算机字长限制导致的舍入误差愈发明显.
3)加速度指标对收敛精度ε的敏感性更高,采用PCG法求解车辆-轨道-地基土耦合系统形成的大型稀疏线性方程组时,建议以加速度指标作为迭代收敛精度的控制指标;可通过选取适当的迭代收敛精度,以达到计算精度和计算效率的平衡,如当关注的振动范围较小时,取较大的ε可减少迭代次数、缩短求解时间.
3.3计算效率分析
为验证本文方法的高效性,采用表3所示的3种不同方法求解车辆-轨道-地基土耦合系统3D随机动力分析中的等效静力平衡方程.其中,Case 1与Case 2的计算方法相同,均采用文献[2]中填充元优化的串行多点同步算法;Case 3采用本文提出的MATLAB-CUDA混合编程的并行PCG方法,迭代收敛精度ε取10-7. Case 1和Case 3均在如表2所示的计算平台上实施;Case 2的计算平台硬件环境[2]为Intel Xeon E5-2620 CPU,内存为64 G.

表4给出了不同方法的计算效率对比结果,其中计算加速比以Case 1一个时间步的计算耗时为基准计算得到.考虑到该算例完整的随机振动计算包含2 000个时间步,而Case 1的总计算时间预计可达180 d左右,故未开展Case 1的全过程计算.

由表4数据可得以下结论:
1)对比Case 1和Case 3可知,相同计算平台下计算一个时间步,本文方法的计算效率是多点同步算法的86.13倍,大大减少了计算耗时,并将总计算时间减少到可接受的3.5 d.
2)对比Case 1和Case 2可知,多点同步算法在不同的计算平台实施时,Case 2的计算效率是Case 1的13.74倍.主要原因是多点同步法[2]属于线性方程组解法中的直接法,对内存的需求大,在内存较小的计算机上使用直接法进行大规模3D有限元方程求解时,会导致计算效率大幅降低.
3)对比Case 1、Case 2和Case 3可知,本文方法采用的稀疏矩阵CSR压缩存储格式和预处理共轭梯度法有效降低了算法的内存需求、提高了计算效率,易于在一般个人计算机上实施计算分析.
4结论
本文结合虚拟激励法与并行的预处理共轭梯度法两种高效算法,提出了一种基于GPU求解车辆-轨道-地基土耦合系统3D随机振动的并行计算方法.通过不同工况的对比分析,得出以下结论与建议:
1)本文方法将GPU并行计算技术应用于车辆-轨道-地基土耦合系统3D随机振动分析,在保证精度的前提下大大提升了计算效率,且对计算机内存的需求小,在一般个人计算机的硬件配置下就能达到较好的计算效率提升,有利于3D模型在随机振动分析中的推广应用.
2)在工程设计中,本文方法有助于更快速地对铁路运输引起的环境振动问题进行评估.例如,使用本文所得结果同时结合3σ法则可高效地确定车辆-轨道-地基土耦合系统随机响应的上下限值.
3)本文方法结合了不同计算平台的优势,采用商业数学软件MATLAB串行处理随机振动计算涉及的大部分运算及计算流程中的各种逻辑控制,通过CUDA调用GPU实现系统等效静力方程的高效并行求解.
4)采用PCG法求解车辆-轨道-地基土耦合系统形成的大型稀疏线性方程组时,建议以加速度指标作为计算精度的控制指标.同时可通过选取适当的迭代收敛精度ε,以达到计算精度和计算效率的平衡.
参考文献
[1]KOUROUSSIS G,VAN PARYS L,CONTI C,et al. Using three-di-mensional finite element analysis in time domain to model railwayinduced ground vibrations[J]. Advances in Engineering Software,2014,70:63—76.
[2]WANG L D,ZHU Z H,BAI Y,et al. A fast random method for three-dimensional analysis of train-track-soil dynamic interaction[J]. Soil Dynamics and Earthquake Engineering,2018,115:252—262.
[3]YANG Y B,HUNG H H. A 2.5D finite/infinite element approach for modelling visco-elastic bodies subjected to moving loads[J]. Inter-national Journal for Numerical Methods in Engineering,2001,51(11):1317—1336.
[4]SHENG X,JONES C J C,THOMPSON D J. Prediction of ground vi-bration from trains using the wavenumber finite and boundary ele-ment methods[J].Journal of Sound and Vibration,2006,293(3/4/ 5):575—586.
[5]GODINHO L,AMADO-MENDES P,PEREIRA A,et al. A coupled MFS-FEM model for 2-D dynamic soil-structure interaction in the frequency domain[J].Computers & Structures,2013,129:74—85.
[6]GALVIN P,ROMERO A,DOMINGUEZ J. Fully three-dimensional analysis of high-speed train-track-soil-structure dynamic interac-tion[J].Journal of Sound and Vibration,2010,329(24):5147—5163.
[7]SI L T,ZHAO Y,ZHANG Y H,et al. Random vibration of an elastic half-space subjected to a moving stochastic load[J].Computers & Structures,2016,168:92—105.
[8]林家浩,張亚辉,赵岩.虚拟激励法在国内外工程界的应用回顾与展望[J].应用数学和力学,2017,38(1):1—32. LIN J H,ZHANG Y H,ZHAO Y. The pseudo-excitation method and its industrial applications in China and abroad[J].Applied Mathe-matics and Mechanics,2017,38(1):1—32.(In Chinese)
[9]LU F,LIN J H,KENNEDY D,et al. An algorithm to study non-sta-tionary random vibrations of vehicle-bridge systems[J]. Computers& Structures,2009,87(3/4):177—185.
[10]ZENG Z P,LIU F S,LOU P,et al. Formulation of three-dimensional equations of motion for train-slab track-bridge interaction system and its application to random vibration analysis[J]. Applied Math-ematical Modelling,2016,40(11/12):5891—5929.
[11]聂旭涛,范大鹏.基于EBE策略实现结构动力响应的并行计算[J].振动与冲击,2007,26(10):51—55. NIE X T,FAN D P. Implementation of structural dynamic response parallel computation based on ebe policy[J]. Journal of Vibration and Shock,2007,26(10):51—55.(In Chinese)
[12]张健.车辆-轨道耦合系统动力学的数值方法研究[D].大连:大连理工大学,2014. ZHANG J.Studies on the numerical methods for dynamics of coupled vehicle-track system[D].Dalian:Dalian University of Technology,2014.(In Chinese)
[13]陈曦,王冬勇,任俊,等. CPU-GPU混合计算构架在岩土工程有限元分析中的应用[J].土木工程学报,2016,49(6):105—112. CHEN X,WANG D Y,REN J,et al. Application of hybrid CPUGPU computing platform in large-scale geotechnical finite element analysis[J].China Civil Engineering Journal,2016,49(6):105—112.(In Chinese)
[14]蔡勇,李光耀,王琥.基于多重网格法和GPU并行计算的大规模壳结构快速计算方法[J].工程力学,2014,31(5):20—26. CAI Y,LI G Y,WANG H. A fast calculation method for large-scale shell structure based on multigrid method and GPU parallel comput-ing[J]. Engineering Mechanics,2014,31(5):20—26.(In Chi-nese)
[15]ZHU Z H,GONG W,WANG L D,et al. A hybrid solution for study-ing vibrations of coupled train-track-bridge system[J]. Advances in Structural Engineering,2017,20(11):1699—1711.
[16]朱志輝,王力东,龚威,等.多种垂向轮轨关系的对比及改进的车-线-桥系统迭代模型的建立[J].中南大学学报(自然科学版),2017,48(6):1585—1593. ZHU Z H,WANG L D,GONG W,et al. Comparative analysis of several types of vertical wheel/rail relationship and construction of an improved iteration model for train-track-bridge system[J]. Jour-nal of Central South University(Science and Technology),2017,48(6):1585—1593.(In Chinese)
[17]WAIVIO N. Parallel test description and analysis of parallel test system speedup through Amdahl’s law[C]//2007 IEEE Autotestcon. Baltimore,MD,USA:IEEE,2007:735—740.
[18]李佳佳,张秀霞,谭光明,等.选择稀疏矩阵乘法最优存储格式的研究[J].计算机研究与发展,2014,51(4):882—894. LI J J,ZHANG X X,TAN G M,et al. Study of choosing the optimal storage format of sparse matrix vector multiplication[J]. Journal of Computer Research and Development,2014,51(4):882—894.(In Chinese)
[19]GEORGESCU S,CHOW P,OKUDA H. GPU acceleration for FEMbased structural analysis[J]. Archives of Computational Methods in Engineering,2013,20(2):111—121.
[20]BIAN X C,JIANG H G,CHANG C,et al. Track and ground vibra-tions generated by high-speed train running on ballastless railway with excitation of vertical track irregularities[J]. Soil Dynamics and Earthquake Engineering,2015,76:29—43.
[21]LIU J B,DU Y X,DU X L,et al. 3D viscous-spring artificial bound-ary in time domain[J]. Earthquake Engineering and Engineering Vibration,2006,5(1):93—102.
