基于弦振动的混沌实验装置研制
2021-02-07丁格曼徐颂华林墁烔叶文超刘家豪谢翠婷
丁格曼 徐颂华 林墁烔 叶文超 刘家豪 谢翠婷
(华南师范大学物理与电信工程学院 广东 广州 510006)
混沌现象起源于非线性系统对初始条件的敏感依赖性,是由确定性方程描述的简单系统出现极为复杂的貌似随机的无规则运动现象.本装置从混沌动力学理论出发,制作弦振动混沌实验装置,利用NI myDAQ数据采集卡和虚拟仪器处理系统,可直观地观察和研究弦线振动由混沌运动向周期有序运动相互转换的过程,并通过Matlab对实验结果进行仿真验证.
1 实验原理
1.1 振动源带动弦线实验中的混沌现象及理论分析
在弦振动实验弦线前加上振动源,当弦线和振动源的连接点调整到接近驻波波节处时,振动系统会形成混沌现象.这种不稳定振荡正是振动源振动端的非线性振动所引起的,此时振动源振动端处于不规则周期运动状态或混沌状态,进而把整个振动系统带入不稳定振动状态[1].
如图1所示,选定弦线固定端点(反射处)为坐标原点x=0,当有阻尼力时,沿x轴反向(即远离振动源方向)驻波振幅不断衰减,距离越大衰减越快.实验中弦线的阻尼小,因此采用弦线作为实验材料,则形成的弦线驻波方程为[2]
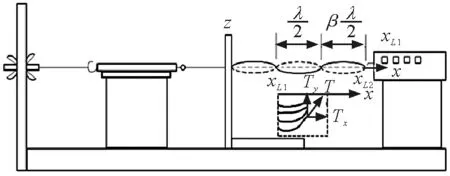
图1 实验振动装置原理图
(1)
其中弦线长度
(2)
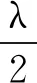
针对振片振动情况进行研究,本实验中振片受振动仪驱动力F驱、振片恢复力F恢和弦线张力T.在上述力的共同作用下进行运动,可得振片的运动状态为
(3)
其中m为振片振动时的有效质量;F恢=-ky;F驱=Focosωt;Ty为弦线张力T的横向分量,即Ty=Tsinθ,θ是振动源与弦线连接处弦线的切线角,如图2所示.
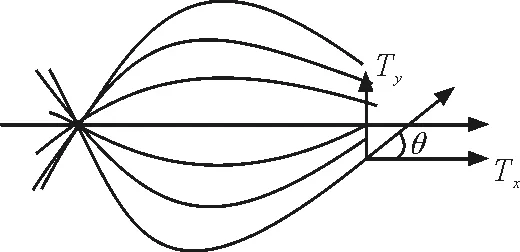
图2 弦线张力分解图
根据图2分析可知,xL处弦线张力的分量Ty对振片振动有作用,而Tx分量并没有作用,因此式(3)中仅含有Ty.切线角θ可通过弦线振动方程来求解,利用式(3)进行分析可知θ满足[2]
(4)
故式(3)可改写为
(5)
其中,y为振片纵向位移;k是振片恢复系数;γ为主要由自身阻尼和弦线张力垂直分量决定的阻尼系数;T是弦线张力;ω为振片振动圆频率.上式就是能产生混沌运动的非线性运动方程.
1.2 驻波实验非线性系统运动的数值分析及仿真
在LabVIEW中内嵌数值模拟部分,即可将实验结果与理论模型进行对比.为了简化计算又不失规律性,将式(5)转化成了无量纲标准型[3]
(6)
其中做了变化,令
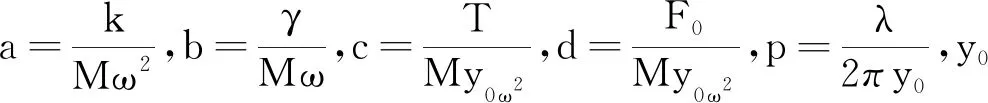
当系统振动起来后,振动仪的驱动力频率与振动系统的固有频率相同,因此式(6)中取a=1.另外根据实验的具体情况,不失一般性地取电磁铁驱动力因子d=0.8,弦线张力因子c=1.0,p=0.637.选择初始条件(X0,Y0)改变β,对式(6)进行数值模拟研究,从而可得到相图和波形时域图,依此来判断混沌现象的发生[4].
根据系统参数a,b,c,d,p,q和初始条件(X0,Y0)的不同情况,利用Matlab对式(6)进行数值模拟研究,得到振动系统的相图和时域图,由此判断系统的振动状态.
根据实验的具体情况,不失一般性地取(b,c,d)=(0.3,1.0,0.5),对β在(0,1)范围内,不同数值进行数值模拟(X0,Y0)=(0.01,0.05),得到相图和时域图如图3所示.结果表明:
(1)β处在(0.22,0.77)范围时,系统振动接近稳定状态;β处在(0.18,0.21)或(0.78,0.81)范围时,系统振动接近混沌状态.
(2)系统处于稳定状态时,时域图接近于正弦波,相图呈现出单个圆形的形状.
(3)系统处于混沌状态时,时域图呈现表面不规律,实际有规律可循的波形,相图出现带“双吸引子”的双圆形状.
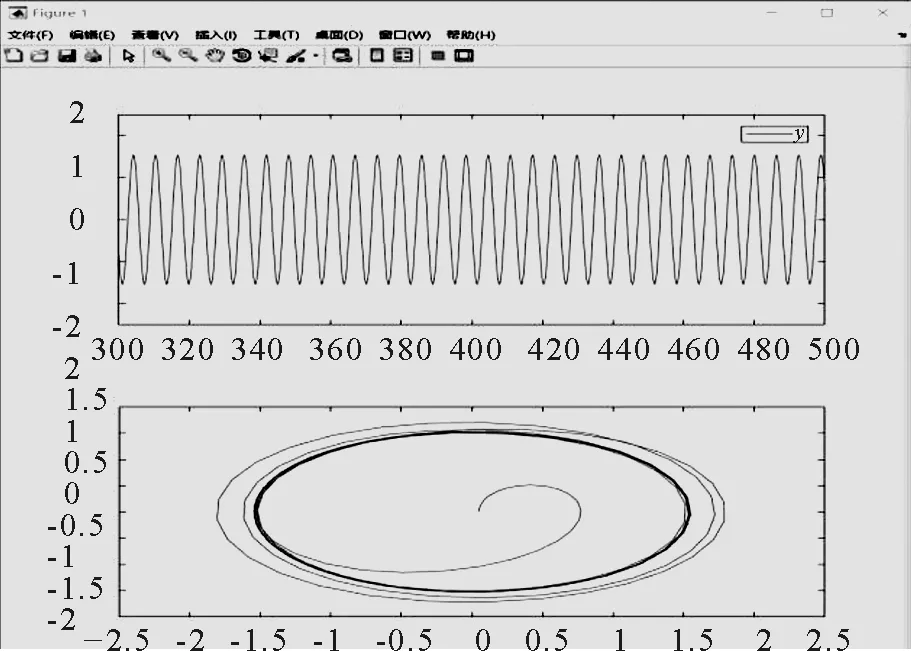
(a) β=0.4时,系统时域图与相图
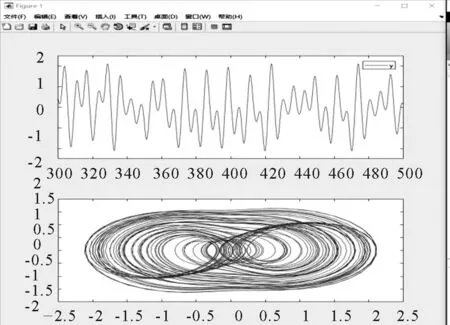
(b) β=0.2时,系统时域图与相图
2 混沌实验装置设计
混沌实验装置主要包括非线性振动平台、电子装置与电路系统、数据采集处理系统3部分.
2.1 非线性振动平台
如图4所示,非线性振动平台主要包括振动源,金属薄片,弦线,驻波显示屏,弹簧测力计,电涡流传感器,尺子等.FD-SWE-Ⅱ弦线上驻波实验仪提供可调节式振源.在振动仪前端延伸固定一个具有较好弹性和小阻尼力的薄金属振片,在金属薄片的一侧设置一个电涡流传感器探头,在振片内部产生电涡流,完成振幅非接触测量的电信号实时转换.薄片的另一端连接弦线穿过一个驻波显示屏(中间带有一小孔的平面板),可控制机械波的反射位置并对驻波波节的位置进行测量.穿过小孔再连接一个弹簧测力计,弹簧测力计固定一个螺旋管穿过木板用螺丝固定,能方便控制弦线张力的大小和连续变化.当条件满足混沌振动时,振片与弦线连接处就会进入混沌振动,从而实现直观和定量测量.
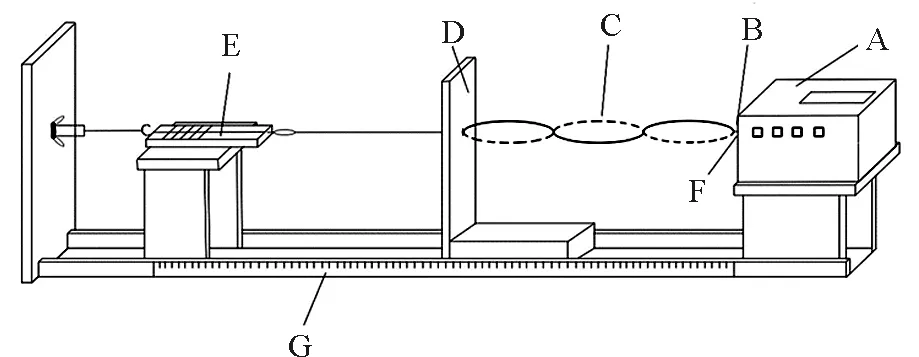
A-振动源;B-金属薄片;C-弦线;D-驻波显示屏;E-弹簧测力计;F-电涡流传感器;G-尺子
图4 非线性振动平台实验装置图
2.2 电子装置和电路系统
装置的电子电路部分包括直流稳压电源、电涡
流传感器、NI myDAQ数据采集卡等.直流稳压电源负责输送-24 V电压供数据采集器使用.弦线振幅的变化由振动源前端金属振片反映,随后将转换成的电信号输出到数据采集系统中.采集的信号数据经过A/D转换,再送入计算机进行处理.具体实现过程为:
(1)将电涡流传感器靠近振动中的铜线.
(2)电涡流传感器感应到铜线振动后,输出电信号给数据采集器电路.
(3)数据采集器将电信号经过处理后产生模拟信号,传递到LabVIEW数据采集卡NI myDAQ中进行处理.
(4)NI myDAQ数据采集卡将模拟信号转化为数字信号,经过放大滤波后传输到计算机.
2.3 数据采集处理系统
利用LabVIEW软件平台,开发数据采集与处理的虚拟仪器,在此虚拟仪器中完成对实验参数的输入、实验数据采集、实验数据处理、实验结果实时展示等功能.其主要程序设计框图如图5所示.
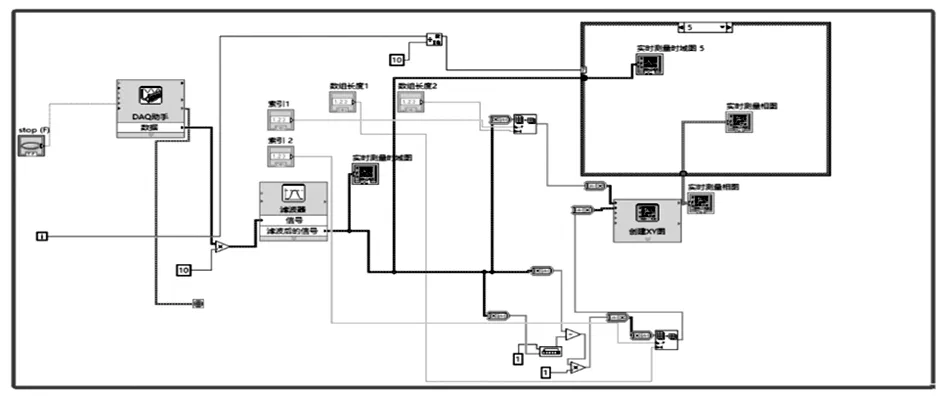
图5 LabVIEW程序设计框图
3 实验观察及数据记录处理
3.1 实验操作
实验前,先调节驻波振动上弦线位置,使其与实验平台保持水平,调节弹簧测力计示数以改变弦线张力,接通驻波振动仪;再打开电子装置控制开关,此时输出端与数据采集卡端口连接,数据采集卡另一端口接地,USB端口与电脑连接,随后启动LabVIEW软件相关程序及MALATB仿真程序,输入相关参数后即可开始实验[5].
以固定频率改变拉力为例,实验操作主要为:
(2)继续微调驻波屏位置,观察此时显示弦线状态的相图和时域图,当相图出现带“吸引子”双圆时,记录此时振动状态及驻波显示屏的位置L.
(3)继续移动驻波显示屏位置,当弦线连接端处于波腹位置附近时,观察时域图与相图,当相图出现单圆时,记录此时振动状态及驻波显示屏的位置L′.
(5)改变拉力大小T,重复以上步骤.
固定拉力大小T不变,改变频率,观察相应时域图与相图,方法类似故不在此详述.
3.2 实验数据记录
通过上述操作,即固定频率改变拉力,数据记录如表1所示.

表1 固定频率f,改变拉力T实验数据记录表
3.3 实验结果与观察
实验过程中,虚拟仪器界面可实时显示驻波显示振片处的振动状态时域图及相图,其中固定频率改变拉力过程中,可观察随着β值的改变,弦振动状态从混沌状态到稳定状态的改变过程,如图6所示.
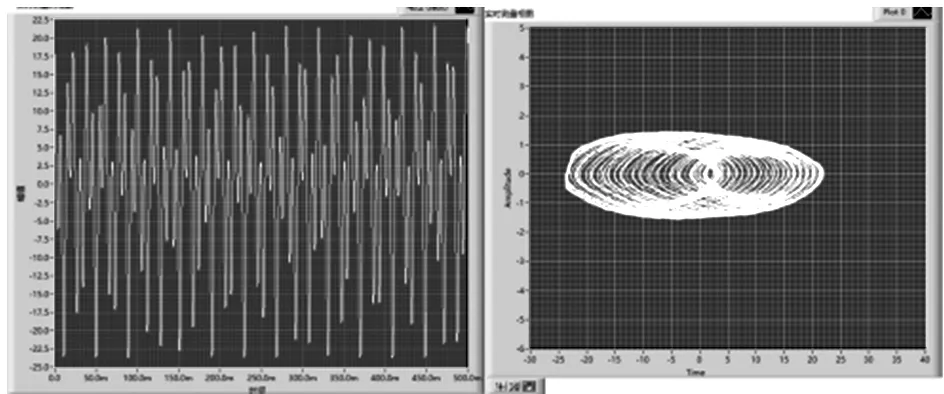
(a) f=128 Hz,T=1.20 N,β=0.20,时域图及相图
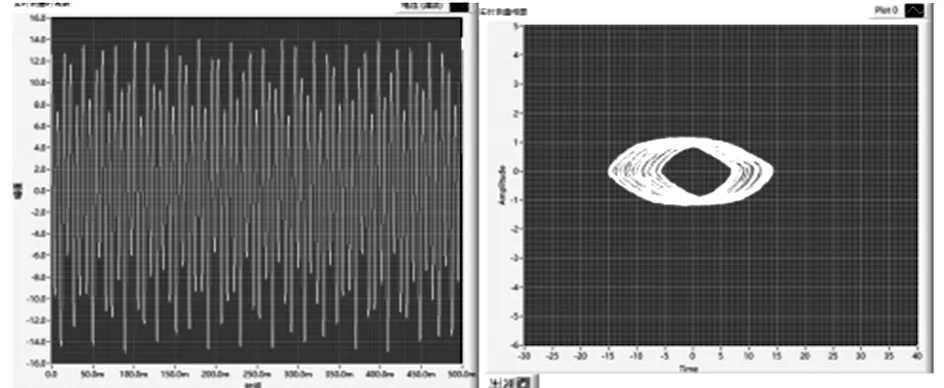
(b) f=128 Hz,T=1.20 N,β=0.56,时域图及相图
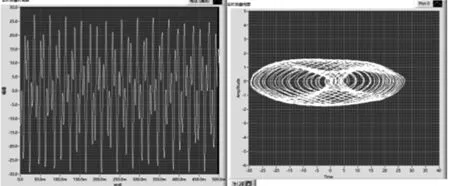
(c) f=128 Hz,T=1.40 N,β=0.18,时域图及相图
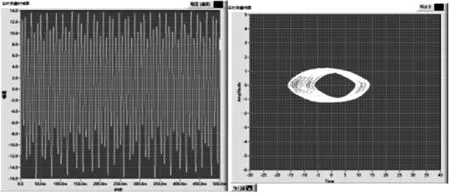
(d) f=128 Hz,T=1.40 N,β=0.48,时域图及相图
4 结论
本实验根据弦线非线性振动理论,结合硬件及软件设计两方面,构建了一套学习和分析该系统中混沌现象的方案,能直观地观察和定量研究该系统由混沌运动向周期有序运动相互转换的过程.当弦线和连接点调整到接近驻波波腹处,弦线处于稳定的振动状态,而调节到接近驻波波节处时,振动系统处于不稳定运动状态.实验中β值在(0.18,0.21)或(0.78,0.81)范围时形成了混沌现象,此时系统的运动过程对初值的依赖性十分敏感.实验装置混沌现象的理论模型和实测数据及实时观察的混沌现象比较吻合.
