创新视角下的立体几何图形变换问题
2021-02-07江苏省无锡市洛社高级中学翟荣俊
■江苏省无锡市洛社高级中学 翟荣俊
立体几何是高考的重要内容,而图形变换问题更是一类常考题型。图形变换,使得立体几何问题由“静态”转为“动态”,并在“动态”过程中生成新的问题加以考查同学们的空间想象能力和抽象思维能力,提升同学们的直观想象的数学素养。图形变换过程中,原图形中的部分几何元素的位置关系、数量关系发生了变化,因此,如何合理分析变换前后图形的关系,特别是抓住动态变换中的几何关系的不变性及相互关系,是解决这类问题的关键。近年来,立体几何中的图形变换问题也出现了一些新的变化。本文旨在通过对立体几何图形中的变换问题进行剖析,为2021 届高三数学立体几何复习提供一些参考。
视角一:平移无形变有形,优化运算显本领
例1(2020年浙江模拟)如图1,在多面体ABCDEF 中,四边形ABCD 为菱形,且∠BAD=60°,在四边形ADEF 中,AF∥DE,∠DAF = 90°,AD=DE=2AF=2,BE =2,M 为AB的中点。
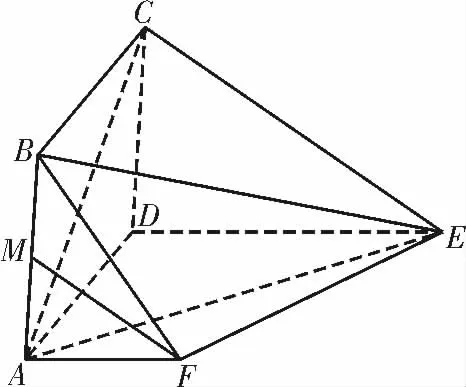
图1
(1)证明:直线FM∥平面EAC;
(2)求直线BF与平面EAC 所成角的正弦值。
解 析:(1)如图2,过E 作EQ∥AD,与AF 的延长线交于点Q。因为AF∥DE,可知四边形ADEQ 为平行四边形,连接BD 交AC 于点S,连接DQ 交AE 于点R,连接RS,所以,MS∥AD。
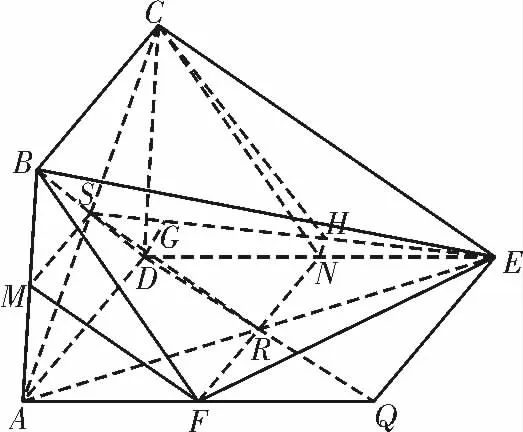
图2
(2)取DE 的中点为N,连接CN,则BF∥CN。
连接BD 交AC 于点S,连接ES,因为DE2+BD2=BE2,所以BD⊥DE。
又因为AD ⊥DE,AD ∩BD=D,所以DE⊥平面ABCD。因为AC⊂平面ABCD,所以AC⊥DE。又因为AC⊥DB,BD ∩DE=D,所以AC⊥平面BDE。
所以平面BDE ⊥平面ACE,作DG ⊥SE 于点G,NH ⊥SE 于点H,则NH ⊥平面EAC,所以∠NCH 为直线CN 与平面EAC所成角,等于直线BF 与平面EAC 成角θ。
点评:本题是一道有一定难度的立体几何问题,空间向量在本题中使用并不方便,解题的关键在于掌握图形中的线面关系,通过平移变换,将线段AD 平移到QE,将线段BF 平移到CN,从而使得原来无形的线面角转化为了有形的∠NCH。可见平移变换,让原本看似很困难的问题转化为了同学们熟悉的考题,也将原本很难运算的空间角问题变得比较方便,优化了运算。
视角二:旋转线动成曲面,曲直结合益解题
例2(2020年山东济南模拟)已知直角梯形ABCD 中,AD∥BC,AB⊥BC,AB=将直角梯形ABCD(及其内部)以AB 所在直线为轴顺时针旋转90°,形成如图3所示的几何体,其中M为弧的中点。
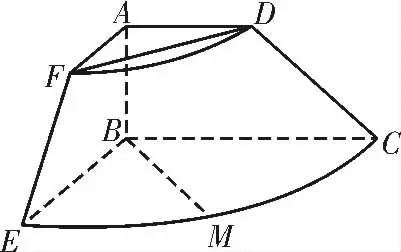
图3
(1)求证:BM ⊥DF;
(2)求异面直线BM 与EF 所成角的大小。
解析:(1)如图4,连接CE,与BM 交于点N。
根据题意,该几何体为圆台的一部分,且CD与EF 相交,故C,D,F,E 四点共面。
因为平面ADF∥平面BCE,所以CE∥DF。
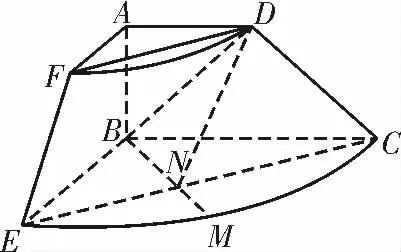
图4
又BC=BE,所以BN ⊥CE,即BM ⊥CE,所以BM ⊥DF。
(2)连接DB,DN,由(1)知,DF∥EN 且DF=EN,所以四边形ENDF 为平行四边形,所以EF∥DN,所以∠BND 为异面直线BM 与EF 所成的角。
点评:本题是一道通过直角梯形旋转得到曲面,进而围成几何体的考题,让同学们直观感受圆台(局部)的形成过程,动静结合,考查了同学们的空间想象能力。两个小题都是围绕几何体中的线线关系展开,考查同学们对于旋转过程中不变量和不变关系的掌握,是否能熟练将空间问题转化为平面问题加以研究和解决。
视角三:翻折化平面为立体,折前折后巧分析
例3(2020年湖北高考模拟)如图5,在梯形ABCD 中,AB∥CD,过A,B 分别作AE⊥CD,BF⊥CD,垂足分别E,F。AB=AE=2,CD=5,已知DE=1,将梯形ABCD沿AE,BF 同侧折起,得到如图6 所示的空间几何体ADE-BCF。
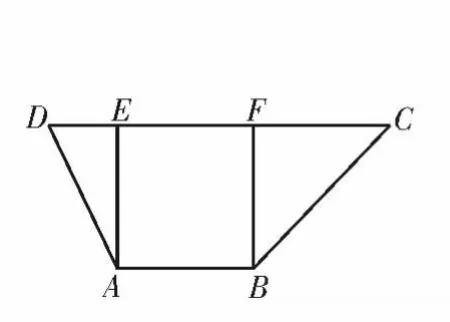
图5
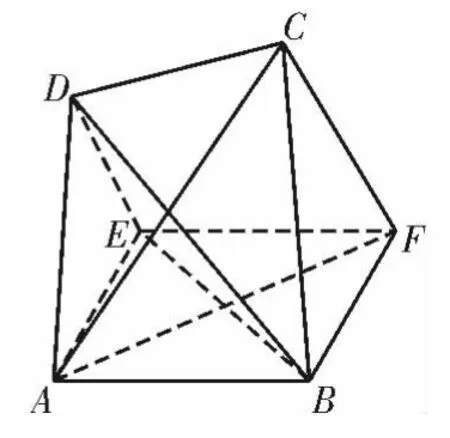
图6
(1)若AF ⊥BD,证明:DE ⊥平面ABFE;
解析:(1)由已知得四边形ABFE 是正方形,且边长为2,在图6中,AF⊥BE。
由已知得AF⊥BD,BE∩BD=B,所以AF⊥平面BDE。
又DE⊂平面BDE,所以AF⊥DE。
又AE⊥DE,AE∩AF=A,所以DE⊥平面ABFE。
(2)在图6中,因为AE⊥DE,AE⊥EF,DE∩EF=E,所以AE⊥面DEFC。
在梯形DEFC 中,过点D 作DM ∥EF交CF 于点M,连接CE。
由题意得DM=2,CM=1,由勾股定理可得DC⊥CF,则
因为DE∥CF,则DC 与DE 垂直,所以CE=2,可得△CEF 为正三角形。
过E 作EG⊥EF 交DC 于点G,可知GE,EA,EF 两两垂直,以E 为坐标原点,以分别为x 轴,y 轴,z 轴的正方向建立如图7所示的空间直角坐标系,则A(2,0,0),B(2,2,0),C(0,1,所以
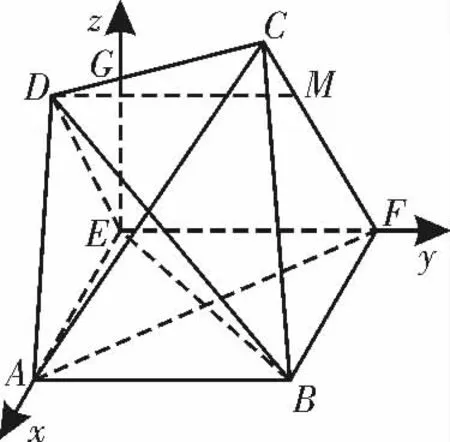
图7
点评:这道考题通过翻折完成了由平面到空间的转化,翻折过程由“动”到“静”,考查同学们是否能正确分析翻折过程中哪些量是不变的,哪些量是改变的。处理此类翻折问题时,通常需要对照分析折前的图形和折后的空间图形,抓住翻折过程中的不变量和不变关系,这样容易对有关线段、角的数量关系及位置关系作出正确判断。
视角四:割补解决局部问题,原有性质要用好
例4(2020年湖南长沙模拟)如图8,多面体ABC-DB1C1是正三棱柱ABC-A1B1C1沿平面切除一部分所得,BC=CC1=1,D为AA1的中点。
(1)求证:BC1⊥平面B1CD;
(2)求点B1到平面BCD 的距离。
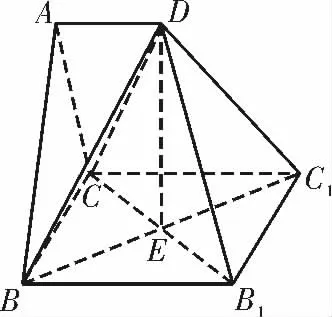
图8
解析:(1)设BC1与B1C 交于点E,连接DE。
因为多面体ABC-DB1C1是正三棱柱ABC-A1B1C1沿平面DB1C1切除部分所得,BC=CC1,所以四边形BB1C1C 是正方形,四边形CC1DA 和四边形ABB1D 均为直角梯形,其中AB⊥AD,AC⊥AD。
因为D 为AA1的中点,AA1平行且等于BB1,所以
因为E 为BC1的中点,所以BC1⊥DE。
又因为B1C⊥BC1,B1C∩DE=E,所以BC1⊥平面B1CD。
(2)设点B1到平面BCD 的距离为d。
因为V三棱锥B1-BCD=V三棱锥D-BCB1,所 以点D到平面BCC1B1的距离即为△ABC 边BC 上的高,即为
点评:本题从一个三棱柱出发,通过切除一部分,完成由“静”到“动”的割补过程,考查同学们对几何图形的理解能力,抓住割补变化后的不变性质。在问题的设置上,重点考查同学们在理解原棱柱性质的基础上,对局部图形的研究。第(2)问的解答中,巧妙地引入了等体积法,将图形变换中的体积转换融入其中,再一次实现了由“静”到“动”的灵活考查。
立体几何中的图形变换问题是高考考查的热点问题,是平面几何与空间几何问题转化的集中体现。纵观近两年的高考试题,图形变换试题的灵活性越来越明显,能力要求也越来越高。处理这类问题的关键是抓住变换前后两图的特征关系,特别是抓住变换过程中的不变元素。
总之,立体几何中的图形变换看似变化多端,实则有规律可循,解答图形变换问题,需要同学们树立信心,掌握解题的常用方法,积极深入地分析问题的特征,才能顺利解答。
