LNG超低温调节阀阀杆流激共振分析
2021-02-06王伟波郝娇山刘柏圻杨恒虎李树勋
王伟波, 郝娇山, 刘柏圻, 杨恒虎, 李树勋
(1.重庆川仪自动化股份有限公司技术中心调节阀研究所,重庆 400707;2.重庆川仪调节阀有限公司,重庆 400707;3.兰州理工大学 石油化工学院,兰州 730050)
近年来,随着国家对清洁能源行业发展的大力推进,海岸线上LNG接收站项目的建设加快了进程。其中,超低温调节阀作为接收站上的关键控制元件,其运行的可靠性极为重要。但由于超低温介质易造成填料损伤,导致填料处泄漏,故此类调节阀阀杆设计都较长,在有散热片的情况下一般须保证填料处温度在0 ℃以上。而对细长阀杆,阀门小开度时剧烈的流体流动极易诱发其共振,对工业的安全稳定运行造成不利影响。因此开展LNG超低温调节阀阀杆的共振研究意义重大。
徐登伟等[1]研发了一种LNG超低温调节阀,建立了其数学模型,进行了低温性能预测,通过低温试验验证了数学模型的正确性,试验结果表明调节阀低温密封性良好;王雯等[2]针对单座式调节阀阀芯阀杆系统的流固耦合振动问题,建立了考虑阀门定位器作用的系统动态仿真模型,给出了求解阀芯-阀杆系统响应的预估-校正算法,利用ANSYS软件对系统在固定开度与变开度情况和流开型与流闭型情况下的振动响应进行了定性分析;刘丽等[3]以某大型化工厂气体管道阀门小开度工况下的振动管路为例,采用模态分析和CFD模拟的方法进行了管道振动分析,结果表明阀后流体脉动是引起管道振动的主要原因,提出了在阀后增设隔板的减振措施,减振效果明显;Yu等[4]为了解决阀门的振动问题,基于模态分析理论,分析了三个典型调压阀的活塞及其支撑结构,得到支撑结构比活塞更刚硬,而刚性活塞对阀门的刚度至关重要;Yonezawa等[5]为阐明由阀门周围的不稳定流动引起的阀芯振动机制,使用刚性和柔性阀头支撑进行实验和数值研究,结果表明,刚性支撑阀头周围的不稳定流动导致阀芯表面上的压力波动具有随机和脉冲波形,柔性支撑阀芯在阀芯支撑系统的固有频率附近振动,且分离喷射的响应滞后于阀芯运动,横向流体力对阀芯上的振动增加了负阻尼。另外申永康等[6]对大型拦污栅结构进行了液固耦合流激振动分析研究;沈春颖等[7]对平面直升闸门进行了流固耦合振动同步测试模型试验研究;李树勋等[8]对高压降套筒式蒸汽疏水阀进行了振动特性研究。
以上研究均未涉及LNG超低温调节阀细长阀杆的流激共振问题,本文将研究流体施加于其阀杆上的激振力频率,以及阀塞阀杆组件在有流体载荷作用时的固有频率,从而对阀杆流激共振问题进行深入研究。
1 LNG超低温调节阀结构模型
本文所研究的LNG超低温调节阀流量调节特性为等百分比调节特性,额定行程为75 mm,最大流量为1 796 t/h,对应的阀门进口压力为0.83 MPa(G),进出口压差为0.05 MPa。各节流开度下的三维实体模型均采用NX软件建立。为方便分析,在不影响分析结果的基础上对3D实体模型的铸字和螺栓孔等进行适当简化,另外考虑到模型从介质进口端至出口端沿中心面对称,固体域和流体域均采用5%、10%、20%、30%和50%开度下的一半模型进行仿真实验,其中20%开度3D实体模型,如图1所示。

图1 LNG超低温调节阀三维实体模型
2 LNG超低温调节阀流场模拟分析
2.1 流道模型建立及网格划分
将所建立的LNG超低温调节阀各开度下的三维实体模型存为.x-t格式,导入ANSYS Fluent软件中,反向建模生成三维流体域模型,流体域和固体域偶合面完全对应,其中20%开度模型,如图2所示。

图2 LNG超低温调节阀三维流体域模型
流道模型网格由ANSYS Meshing划分生成,整体采用四面体/混合网格控制,尺寸较小的局部区域采用六面体网格控制。以20%开度流体域模型为例进行网格无关性检验说明,将稳态模拟得到的调节阀出口流量值及出口流体平均流速作为评判依据,具体网格无关性检验数据,如表1所示。

表1 流体域网格无关性检验数据
由表1可知:网格数从502 279增大到711 620时,流量从8.890 46 kg/s变为8.865 54 kg/s,减小0.28%,速度从1.531 28 m/s变为1.542 75 m/s,增大0.75%。网格数从711 620增大到907 157时,流量从8.865 54 kg/s变为8.862 36 kg/s,减小0.036%,速度从1.542 75 m/s变为1.543 94 m/s,增大0.077%。相比较而言,当网格数达到711 620以上时,流量及速度的变化量可以忽略不计。同时考虑模拟计算精度、时间成本和工作量,以网格数为711 620的流道网格模型作为LNG低温调节阀20%开度时的最终流场仿真模型,具体网格模型,如图3所示。

图3 LNG超低温调节阀20%开度流体域网格模型
2.2 流场模拟计算理论
基于连续性方程、动量方程和能量方程,LNG超低温调节阀流场计算采用RNGk-ε湍流双方程构成封闭方程组,其理论方程如下[9]。
(1)湍动能k方程:
(1)
(2)湍流耗散率ε方程:
(2)
式中:Gk为平均速度梯度引起的湍动能生成项,ρ为介质密度,μ为介质黏度,其中:
(3)
(4)
(5)
(6)
(7)
Cμ=0.084 5,C2ε=1.68;αk=αε=1.39
(8)
2.3 不同开度流场瞬态分析
非定常流场及压力脉动的研究大多应用在泵和水轮机上[10-12],本文针对LNG超低温调节阀阀杆流激共振问题,对各开度模型进行流场瞬态分析。
入口设置总压0.931 325 MPa,出口为静压0.881 325 MPa;壁面边界采用标准壁面函数;介质为-162 ℃ LNG,黏度为0.000 133 Pa·s,密度为453.3 kg/m3;Time Step Size设置为0.000 5 s,Number of Time Steps为1 000。
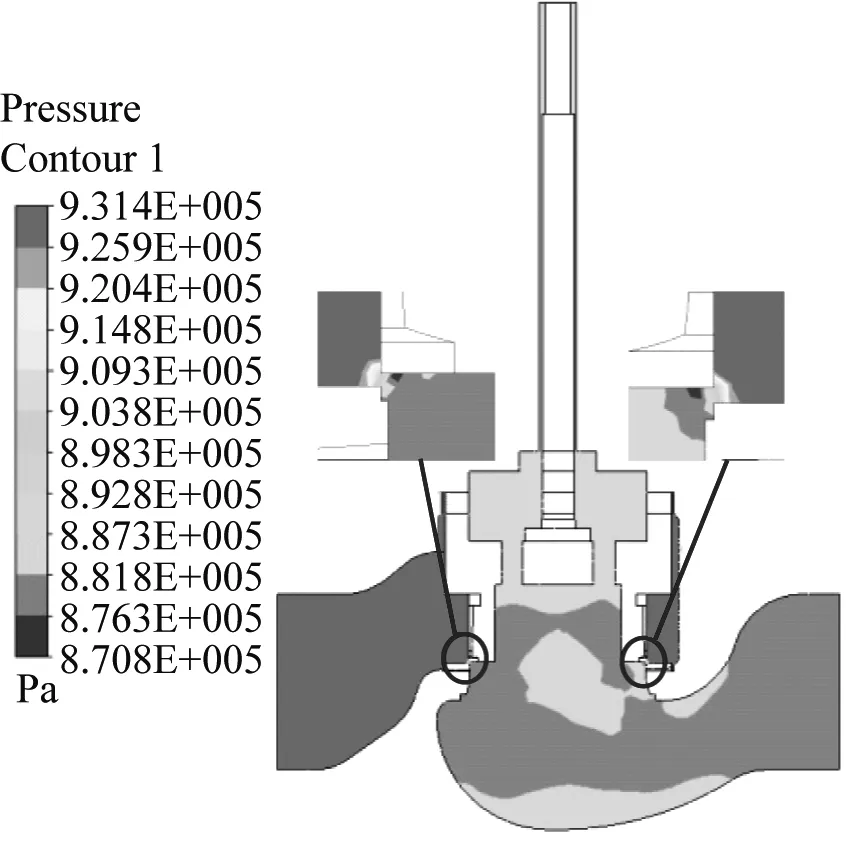
以LNG超低温调节阀5%、20%和50%开度0.5 s时刻流场云图为例,研究阀门从5%到50%开度过程中的流体流动特性,分别如图4~6所示。
(a)横截面压力分布云图

(a)横截面压力分布云图

(a)横截面压力分布云图
由图4~6可知:调节阀开度从5%~50%增大的过程中,在阀塞与阀盖及上套筒之间逐渐形成较小的旋涡,且随开度的增加旋涡逐渐增多,在下套筒内部至阀门出口,始终都形成有较大的旋涡;最大流速均分布在节流区域,最小流速均分布在阀塞与阀杆之间的缝隙处;最大湍动能从节流区域逐渐过渡到阀塞压力平衡孔处,最小湍动能均分布在阀门节流前区域、阀杆与阀盖间隙处;最大压力始终位于阀门进口至下套筒节流之前区域,节流前后压力变化逐渐趋于平缓。另外由最小流速和最小湍动能位置可判断,阀塞与阀杆之间的缝隙处流体流动非常缓慢,几乎处于静止状态。
2.4 流体激振频率分析
对调节阀各开度阀塞和阀杆流固耦合面压力脉动时域信息进行监测,20%开度监测面,如图7所示。
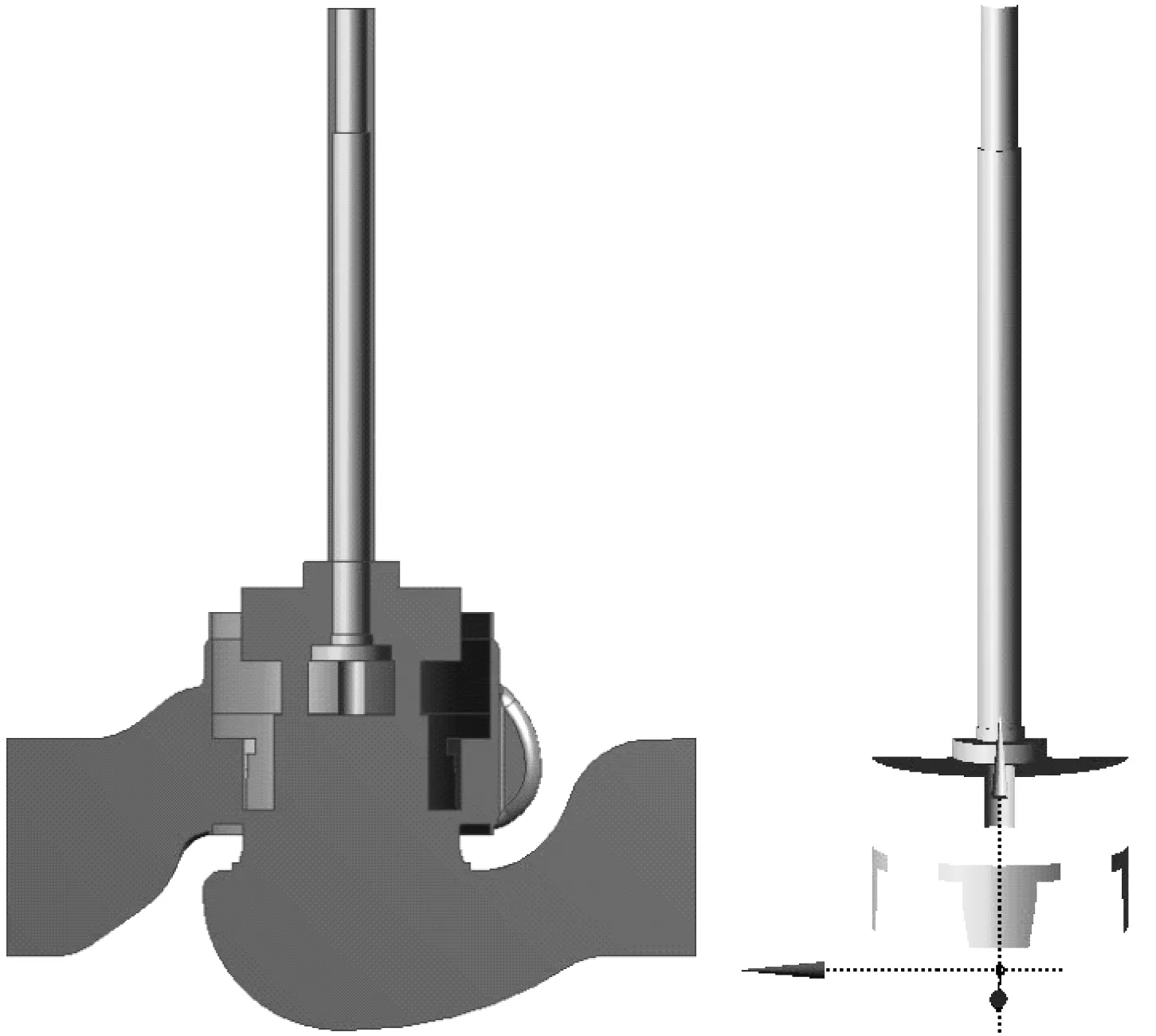
图7 调节阀20%开度阀塞和阀杆流固耦合监测面
在0~0.5 s时间段内,对阀塞和阀杆流固耦合面上的压力脉动时域信息进行数据提取,并通过Tecplot软件对阀门5%、10%、20%、30%和50%开度阀塞和阀杆流固耦合面上的压力脉动时域信息进行傅里叶变换,得到流体作用于阀杆上的压力脉动频谱图,如图8所示,其中压力脉动峰值频率即为流体激振力频率。

图8 各开度流固耦合监测面压力脉动频谱图
由图8可知:调节阀开度从5%~50%增大的过程中,阀塞和阀杆组件上的压力脉动波动幅值逐渐降低。各开度下的压力脉动峰值频率均在60 Hz以内,其中5%开度时,压力脉动峰值频率为32.032 Hz;10%开度时,压力脉动峰值频率为10.01 Hz、18.018 Hz、52.052 Hz;20%开度时,压力脉动峰值频率为16.016 Hz;30%开度时,压力脉动峰值频率为18.018 Hz;50%开度时,压力脉动峰值频率为14.014 Hz、20.02 Hz、26.026 Hz。
3 LNG超低温调节阀模态分析
目前对阀门固有频率的研究大都是基于干模态的方法[13-16],并未考虑流固耦合[17]作用对阀门模态的影响。对LNG超低温调节阀,在现场使用中需进行保温处理,故本文对其开展流固耦合分析,再在耦合基础上进行阀塞阀杆组件的模态分析。
3.1 流固耦合模态分析模型建立
(1)在ANSYS Workbench软件中联用流场、静力场与模态分析模块,并将各开度的实体模型导入Fluent中,反向建模生成内部流道模型,对其进行前处理及网格划分,设置模型边界条件、流体属性以及求解方式,进行流场的求解。
(2)将流场的求解信息导入到静力场,在静力场进行材料设置、实体模型网格划分、约束条件设置以及流场信息的加载,得到流固耦合边界压力信息,进行静力场求解。
(3)将静力场中求解的信息导入到模态分析模块,进行模态阶数的求解设置,完成调节阀模态分析模拟计算。
3.2 流固耦合模态分析计算理论
LNG超低温调节阀流固耦合模态分析计算理论方程如下[18]。
(1)流体诱发固体振动和位移的控制方程:
(9)
(2)耦合控制方程:
(10)
(3)有预应力的模态方程:
(11)
式中:Ms为结构体质量矩阵,Cs为结构体阻尼矩阵,Ks为结构体刚度矩阵,rs和rf分别为流固耦合面固体位移和流体位移,τs和τf分别为流固耦合面固体应力和流体作用力,ωi为结构体第i阶固有频率,{φi}为结构体第i阶阵型向量。
3.3 流固耦合模态分析模型前处理
流固耦合分析需定义流体耦合面和固体耦合面,且为确保计算的准确性,流体耦合面和固体耦合面完全对应,完成流体压力信息向结构体的传递,进而完成流固耦合模态分析,20%开度耦合面,如图9所示。

(a)流体耦合面
3.4 材料参数
LNG超低温调节阀阀体、阀盖、套筒、阀塞和阀杆等组件均需在液氮中进行深冷处理,其性能参数根据《ASME BPVC SECT.Ⅱ Part D, 2015 ED》[19]查询得到,主要零部件材料性能参数,如表2所示。
3.5 固体域网格划分
稳态流场计算完成后,将其压力信息导入结构场中,在结构场中根据表2进行材料性能参数设置,并采用ANSYS Meshing软件的自适应网格划分技术对固体域模型进行网格划分,20%开度网格模型,如图10所示。
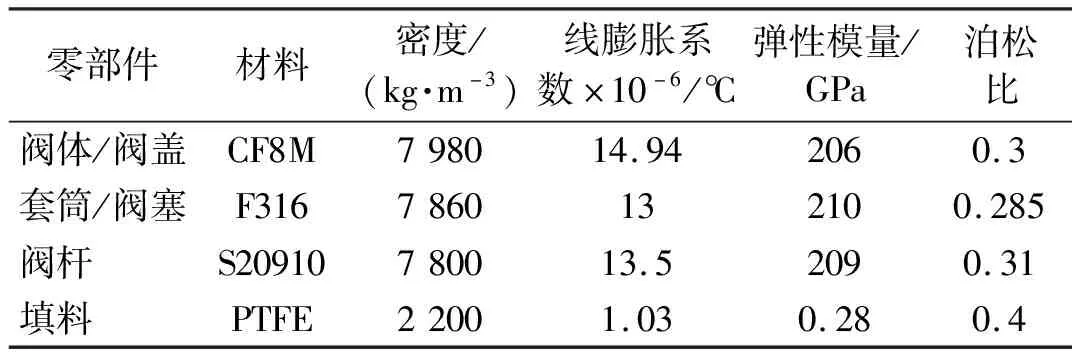
表2 主要零部件材料物理性能参数
图10 LNG超低温调节阀固体域网格模型
3.6 流固耦合边界分析
根据LNG超低温调节阀各零部件的实际安装方式进行接触设置,施加重力载荷,阀体两端面施加位移约束,内腔压力由流场传递,20%开度流固耦合边界如图11所示。

图11 LNG超低温调节阀流固耦合边界
由图11可知,流体作用于固体域的最大压力为0.931 129 MPa,主要位于阀体、阀盖和阀塞内腔面,最小压力为0.321 837 MPa,主要位于下套筒节流部位、阀塞平衡孔处和阀盖下端面处。
3.7 流固耦合应力变形分析
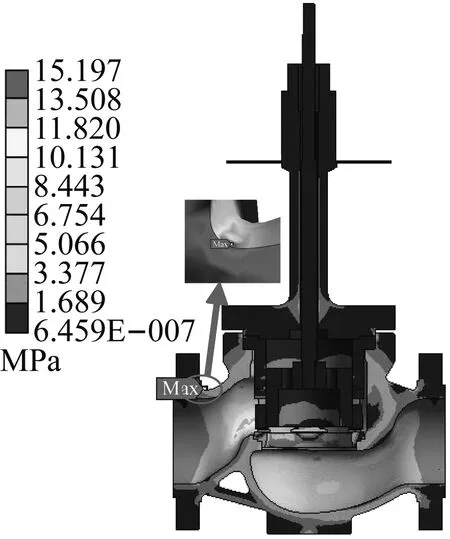
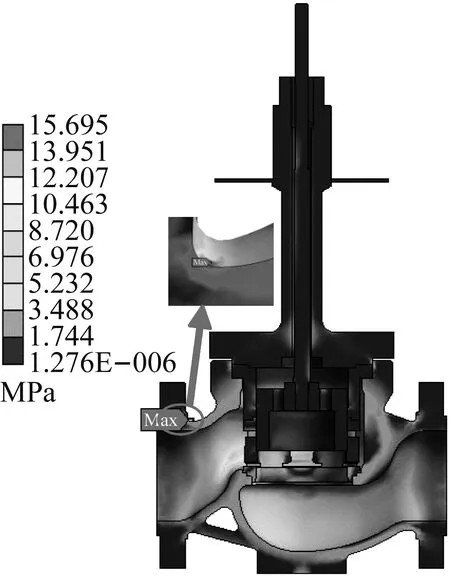
为方便研究LNG超低温调节阀从5%~50%开度过程中流体流动对其应力变形的影响,取5%、20%及50%开度结构场应力变形云图进行分析说明,分别如图12~14所示。
(a)应力云图
(a)应力云图
由图12~14可知:调节阀开度从5%~50%增大的过程中,调节阀整体最大流固耦合应力均在15.3 MPa左右,均位于介质进口侧阀体法兰端结构突变处;调节阀整体最大流固耦合变形量均在0.045 mm左右,均位于填料最底端区域;5%开度时阀杆挤压填料左侧程度大于右侧,导致填料底端左侧变形量较大;20%和50%开度时,阀杆挤压填料右侧程度大于左侧,导致填料底端右侧变形量较大。
3.8 模态分析
(1)模态振型分析
对LNG超低温调节阀进行有预应力(介质压力)的结构模态频率求解,由于高阶模态频率和振型可以看作若干个低阶模态和振型的组合,故在调节阀5%、10%、20%、30%和50%开度时,分别对阀塞和阀杆组件进行前6阶结构模态仿真实验,获得各开度下其前6阶固有频率。
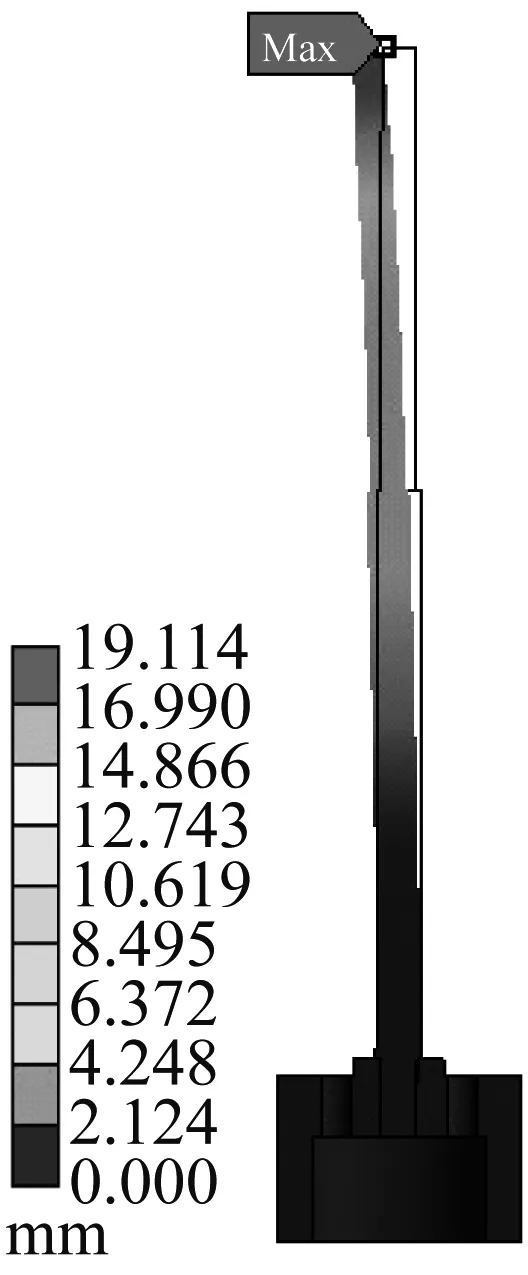
为方便研究LNG超低温调节阀从5%~50%开度过程中流体流动对其振型的影响,取5%、20%及50%开度阀塞和阀杆组件的第一、二阶模态振型云图进行分析说明,分别如图15~17所示。

(a)一阶模态振型

(a)一阶模态振型
(a)一阶模态振型
由图15~17可知:调节阀开度从5%~50%增大的过程中,阀塞和阀杆组件最大一、二阶流固耦合模态变形量均呈增大趋势;调节阀各开度下,二阶模态最大变形量均大于一阶模态最大变形量;调节阀5%开度时,阀塞和阀杆组件一阶最大流固耦合模态变形位置在阀杆端部左侧部位,二阶在阀杆端部右侧部位;调节阀20%和50%开度时,阀塞和阀杆组件一阶最大流固耦合模态变形位置在阀杆端部右侧部位,二阶在阀杆端部左侧部位;一阶流固耦合模态振型均以阀塞和阀杆连接处为支点,阀杆沿垂直于流体流动方向的中心面左右摇摆;二阶流固耦合模态振型均以阀塞和阀杆连接处及阀杆与填料接触处为支点,阀杆沿垂直于流体流动方向的中心面左右弯曲。
(2)模态频率分析
LNG超低温调节阀5%、10%、20%、30%和50%开度时的模态频率,如表3所示。
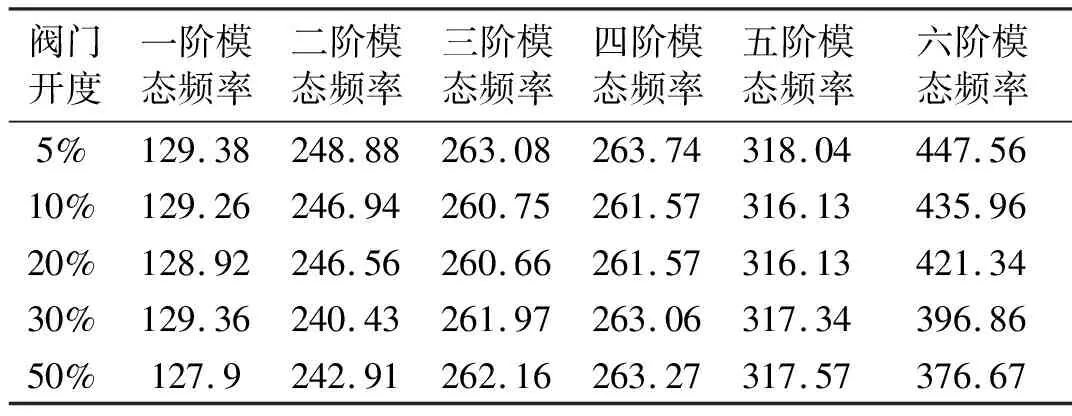
表3 LNG超低温调节阀各开度下阀塞和阀杆组件模态频率
由表3可知:调节阀开度从5%到50%增大的过程中,前五阶模态频率相差较小,第六阶模态频率相差较大,且呈现递减趋势;随着模态阶数的增大,调节阀各开度下模态频率均呈递增趋势;前六阶模态频率均大于120 Hz。
4 LNG超低温调节阀阀杆共振分析
LNG超低温调节阀介质压力脉动作用在阀塞和阀杆组件上,相当于给阀杆施加了一个激振力,当阀杆的某阶固有频率恰好等于或接近压力脉动的峰值频率时,就容易引起阀杆的共振,导致调节阀噪声增大,损害工作人员健康,甚至造成阀杆的损毁失效,对工业生产带来不可预计的损失。
根据上述分析,调节阀在5%、10%、20%、30%及50%开度,阀塞和阀杆组件上的压力脉动峰值频率均在60 Hz以内,其前六阶模态频率均大于120 Hz,两种频率值没有相等和接近,因此阀杆不会发生流激共振。
5 结 论
本文针对LNG接收站超低温调节阀细长阀杆的流激共振问题,对固体域铸字和螺栓孔等进行了适当简化,且考虑LNG介质对阀体、阀盖、套筒、阀塞和阀杆等组件线膨胀系数和弹性模量等性能参数的影响,基于瞬态流场数值模拟和流固耦合模态分析,对其5%、10%、20%、30%及50%开度模型进行了深入研究,得出以下结论:
(1)调节阀从5%~50%开度,阀塞与阀盖及上套筒之间形成的小涡逐渐增多,阀杆与阀盖间隙处流体流动非常缓慢,几乎处于静止状态,节流区域流速最大,压力变化剧烈,阀塞和阀杆组件上的压力脉动波动幅值逐渐降低,各开度下的压力脉动峰值频率均在60 Hz以内。
(2)调节阀开度从5%~50%,介质进口侧阀体法兰端结构突变处出现由应力集中导致的最大流固耦合应力,填料底端出现最大变形。
(3)一阶流固耦合模态振型中阀杆呈摇摆运动,二阶流固耦合模态振型中阀杆呈弯曲运动。阀塞和阀杆组件上各阶模态频率均大于120 Hz。
(4)调节阀各开度下,阀塞和阀杆组件上的压力脉动峰值频率均避开了其固有频率,阀杆不会发生流激共振。
