柔性环形防护网顶破受力归一化分析
2021-02-06余志祥张丽君李自名
齐 欣, 余志祥,张丽君,许 浒, 李自名
(1.西南交通大学 土木工程学院,成都 610031;2.西南交通大学 防护结构研究中心,成都 610031)
柔性防护网是由钢丝绳、钢丝等具有较高抗拉强度的金属材料,通过缠绕、编制等工艺手段而成的具有一定刚度的结构物。柔性防护网在施工防坠落、高楼防坠物、公路沿线防坠物、山区落石防护等许多工程防护领域中广泛使用[1]。常见的柔性防护网有:菱形网、双绞六边形网、G.T.S网、环形网等,其中环形柔性防护网是金属柔性防护网中应用最为广泛,也是最重要的一种形式。柔性环形网通常由多个圆环相互套结而成,遭受冲击作用时,一方面,依靠网环大变形使冲击荷载作用持续时间延长了4倍~8倍,冲击力降幅达50%以上[2];另一方面,环形网在工作中将力传递给柔性防护系统中的其他支撑构件,实现系统协同工作,有效降低了钢柱和钢丝绳的内力,提高了系统整体的工作性能[3],并能承受落实的累计多次冲击[4]。
柔性防护网是柔性防护结构的重要组成部分,其本身的大变形、大位移涉及到复杂的结构非线性问题,因此各国学者广泛开展了柔性防护网的相关研究,Grassl等[5]设计了单跨网的试验机,对尺寸为3.9 m×3.9 m的柔性环形网进行了冲击试验,修正了数值模拟的网片单元。Gentilini等[6]针对不同防护等级的防护系统,将网环等代为菱形或者三角形单元,并将仿真结果与试验结果对比,建立了由圆环单元和三角形桁架单元构成的数值模型。汪敏等[7]采用数值分析对环形网耗能因素进行了参数分析,并与理论结果进行了比较。Castro-Fresno等[8]开展了集中力和局部荷载作用下,网片的顶破试验研究,讨论了两种试验方法下,试验结果的差异。Escallón等[9]对柔性环形网的准静态拉伸和落石冲击开展了数值模拟,结果表明环与环之间的接触具有增塑效应,并确定了滑动摩擦、接触、损伤行为以及应变率相关材料特性参数。Yu等[10]研究表明柔性环形网的冲击变形受钢丝股数、边界特性的影响,变形量相对稳定,约占系统变形的30%~40%。赵雅娜等[11]通过网环拉伸试验与数值模拟计算的方式得到了各典型变形状态下,网环的荷载位移关系,建立了分区等代计算模型。Albrecht等[12-15]开展了静力拉伸试验并将静力结果指导试验和数值分析,见图1。

(a)落石边坡防护
文献[6-14],均采用静定拉伸试验和动态冲击试验相对比的方式对网片性能进行了研究,两种试验方法下均取得了较好的一致性结果,表明环网的静力试验和动态冲击试验具有相似性。因此,欧洲行业标准EOTA、中国铁路行业标准(TB-T3089—2004)和公路行业标准(JT-T528—2004)均要求在产品投入使用前,开展网片、环链的静力拉伸试验,确定其极限拉力。
现有文献的研究主要集中于柔性防护网的数值建模、平面内的静态拉伸和防护网能量的耗散,鲜有柔性环形网的平面外顶破分析。而在实际工程中,柔性防护网长时间承受平面外荷载,其破坏也主要由平面外的顶破所引起,见图2。
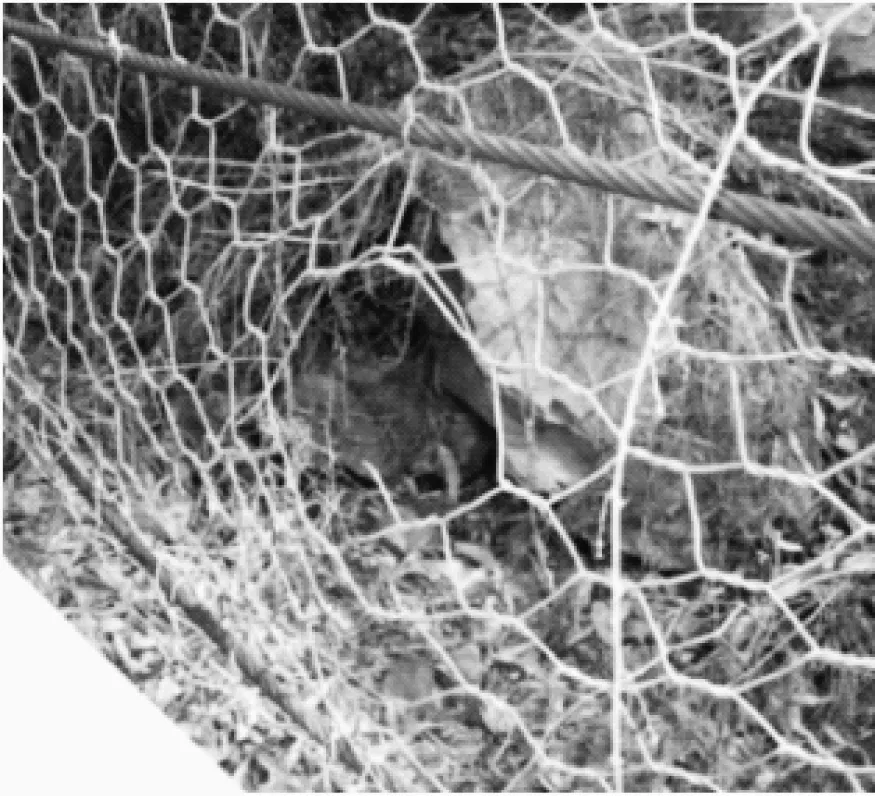
图2 柔性防护网冲破
基于此,本文通过柔性环形网平面外的顶破试验,明确柔性环形网的力学性能,并结合数值模拟,开展参数分析,为今后柔性防护网结构的研究提供参考。
1 理论分析
柔性环形网由多个单环套接而成,单个圆环通常与其它四个圆环相互套结,单个圆环的受力简图如图3(b)。由对称结构及弹性理论分析可知,单环双向对称,受力双轴对称。其轴力对称,剪力反对称,弯矩对称,转角反对称,因此B截面竖向位移、水平位移和转角位移均为零,解除A截面约束,固定B截面,由力的平衡条件并取四分之一结构为计算单元见图3(d)。由文献[15]并结合经典力学中的能量法和单位荷载法,可得内力表达式如式(1)~式(3),单环的内力分布图(图4(a)~4(c))。

(a)
(1)
(2)
(3)
A点为直接受力点,从图4中也能看出,A点弯矩大于B点弯矩,A点率先形成塑性铰,M0为截面的极限弯矩,此刻FP值:

(a)弯矩图
(4)
A点形成铰后,拉力继续增大,而后B截面形成塑性铰。此刻FP值:
(5)
其截面上三种内力共同作用:弯矩M, 轴力FN和剪力FS,略去剪力FS对屈服条件的影响,则在弯矩和轴力联合作用下的屈服曲线的方程是:
|m|+n2=1
(6)

当A、B均处于屈服状态后:
(7)
最终,在弯矩和轴力的共同作用下,单环在A点发生破坏。多环套接后,圆环的边界与相互套结的圆环刚度相关,环套结后的圆环受力更趋于均匀。扩展至整体的柔性环形网,还需要考虑环网之间的滑移与错动,其受力更加复杂,因此,开展专项的整体柔性环形网的分析十分必要。
2 柔性环形网平面外顶破试验
2.1 试验模型
单个圆环是由直径3 mm,抗拉强度不少于1 770 MPa的钢丝盘结一定的圈数,见图5(a),多个圆环相互套接形成整体柔性网,见图5(b)。

(a)
本文首先开展6组不同缠绕圈数的环形网平面外顶破试验。试验工况如表1所示,其中R5/3/300中的R5表示圆环的钢丝缠绕5圈,3表示钢丝的直径是3 mm,300表示圆环直径是300 mm。

表1 试验工况
2.2 试验装置及测试方法
试验装置由加载设备、顶破试验架、数据采集仪、位移传感器等部件组成。水平试验架四周设有定位孔,柔性环形网通过定位孔连接于试验架,见图6。

图6 试验装置
加载时,加载端预置于环形网面下,经由液压作动器提供竖直向上准静态位移,顶头缓慢提升后与网面发生接触。该过程中当加载顶头底面与网面等高时,认为试件初始松弛量被消除,此状态作为标定初始状态。加载端位移加载速率为7 mm/min。当拉力测试值达到峰值并极速下降时,停止加载。摄像机记录顶破试验过程,数据采集系统记录环形网加载历程的顶压力、顶压位移。其中,拉力传感器为1 000 kN,精度为0.3%;拉线式位移传感器,量程>1.5 m,精度0.3%。位移与拉力量测值通过数据采集系统实现同步。反力架的内部空间3.15×3.15 m,试验网片为3 m×3 m。
2.3 试验过程及结果
2.3.1 试验过程
试验开始后,随着加载端提升,圆环相互滑动,网片绷紧。环形网不断被拉伸,圆环内力逐步增大。与加载端直接接触的中心圆环由正圆转变为椭圆,最终形成梯形;与边界卸扣直接相连的圆环,从正圆转变为椭圆,最终形成三角形;中部圆环由正圆转变成椭圆状,最终形成矩形。环形网由初始水平状态转化为倒扣的漏斗状。最终,加载端边缘圆环突然断裂,环形网失效,试验结束,见图7。

图7 顶破试验
2.3.2 试验结果分析
试验后,提取出各工况的荷载-位移曲线,见图8(a)。曲线呈现出三个阶段:第一个阶段:顶破力平缓增长,拉伸位移快速增加。网片逐渐张紧,但在前期圆环内轴力较小,在弯矩的作用下圆环发生大变形,曲线缓慢上升;各条曲线在第一阶段基本保持一致。第二阶段:随着位移逐渐增大,网片张力开始非线性上升,圆环内轴力急剧增加,弯矩减少,在弯矩和轴力的共同作用下圆环变形减缓。随着缠绕圈数的增加,第二阶段的斜率加大,表明其顶破力增长速率加快。第三阶段:弯矩不变,圆环在轴力作用下塑性流动,圆环变形很小,当荷载达到顶破力极值,圆环钢丝破断,网片顶破,第三阶段的各曲线斜率基本保持一致。
提取各工况下的破断力和破断位移,并进行拟合,见图8(b),破断力随着圈数的增加明显呈线性增长,从缠绕圈数5圈的环形网到缠绕圈数16圈的环形网,破断力从318 kN增大到904 kN。极限拉伸位移随着圈数的增加线性小幅减小,从1 022 mm降低到917 mm。

(a)力——位移曲线
3 有限元分析
为了进一步对柔性环形网的力学性能进行分析,采用LS-DYNA模拟试验全过程。有限元模型对试验进行了简化,简化后模型包括三部分:环形网,固定端(仅保留卸扣用于连接、固定环形网),加载端。环形网、卸扣采用非线性梁单元,加载端采用实体单元。各部分的材料特征如表2。加载端与网片设置梁单元与面单元的接触,圆环之间为梁与梁接触,并考虑相对滑移。卸扣顶点将其三个方向自由度全部约束。数值模拟中的参数与试验保持一致。具体模型建立及边界设定方法见文献[17-20],加载端通过位移加载,加载速度为1.2×10-4m/s,不断提升加载端,施加给网片顶破力,直至环形网单元达到极限应力,单元失效,环形网破坏。

表2 模型材料特性
3.1 试验与有限元结果对比
数值模拟加载变形过程如图9。完整重现了试验的全过程。第一阶段,网片从松弛状态转变为紧绷;第二阶段,边界处的网环从圆转变为三角形;第三阶段,圆环转变成三角形和梯形。最终圆环应力达到1 770 MPa,圆环破断,环形网破坏。
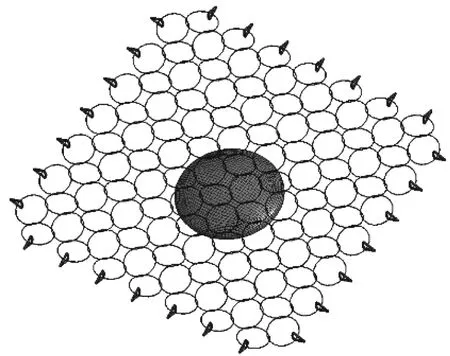
图9 网片变形过程
选取5、6、7圈的网片试验与数值模拟结果进行对比见图10,二者吻合的较好,数值模拟中所得的破断力略大于试验结果。二者在第一阶段稍有偏差,其原因在于,试验时为保证环形网平整,预先进行了张紧,即试验的初始值不为零,但数值模拟中环形网呈现自然状态,二者略有差别。同时数值模拟中加载端严格位于环形网正下方,而试验中网片安装时位置略有偏差。

图10 数值仿真与试验对比
4 顶破力学性能参数分析
实际工程中,环形网的尺寸规格各异,为了探求各种不同规格的环形网力学性能,分别建立了19组模型,进行单参数分析,分析圆环直径、加载端与环形网面积比,长宽比对网片力学性能的影响,见表3。

表3 计算参数
4.1 圆环直径的影响分析
保持环形网面积不变,分别建立圆环直径D为200 mm、250 mm、300 mm、350 mm和400 mm的模型。从图11可看出,第一阶段,四条曲线基本重合,但随着圆环直径的增加,第一阶段到第二阶段的分界点所对应的位移持续增大,说明加载端与环形网接触后,圆环直径越大,整体变形也越大。第二阶段,四条曲线平行上升,速率基本一致。从图11(b)可以看出,破断力随着网片圆环直径的增加呈指数函数明显降低。极限拉伸位移随网环直径的增大而线性增大。

(a)力——位移曲线
4.2 加载端与网片面积比的影响分析
保持环形网面积不变,改变加载端直径,分别选取直径为0.6 m、0.8 m、1 m、1.2 m和1.5 m。加载端和环形网的面积比S分别为0.04、0.05、0.09、0.16、0.20。
从力——位移曲线看出,第一阶段,各条曲线基本重合。第二和第三阶段,随着面积比的增大,曲线斜率小幅减小。随着加载端与环形网面积比的增大,自由环数随之减小,圆环之间的初始总空隙减小,网片的总弹性变形减小,从而圆环在达到破断之间可拉伸变形减小,极限拉伸位移随着减小。同时更多的圆环共同承担荷载,破断力随之减小。总体而言,随着加载端与网片面积比的增大,破断力和极限拉伸位移都呈幂函数持续减小,变化速率基本一致。

(a)力——位移曲线
4.3 长宽比的影响分析
保持环形网面积不变,改变环形网的长度和宽度,分别选取(3 m×3 m、2.63 m×3.42 m、2.45 m×3.67 m、2.24 m×4.02 m和2.12 m×4.25 m)长宽比λ分别为1.0、1.3、1.5、1.8和2.0。从图13(a)可以看出,各条曲线在第一第二阶段基本保持一致,随着长宽比的增大,环形网快速的进入到第三阶段,并随之破坏。长宽比越接近1的环形网,能更好的把荷载分散到各个圆环上,具有更好的变形能力并能承受更大的荷载。长宽比越大更容易形成应力集中,局部圆环变形过大,而其他区域圆环变形过小,过早达到网片的极限拉伸位移,导致环形网过早破断。破断力和极限拉伸位移都呈幂函数减小,破断力的减小更为明显,破断力急剧降低。

(a)力——位移曲线
5 力-位移曲线归一化公式
为了更好的研究环形网的受力性能,对环形网平面外的极限拉伸位移和力——位移曲线进行归一化。
5.1 极限拉伸位移
假定环形网尺寸为HB(H≥B),达到临界破坏状态时,极限拉伸位移OA、短边半边长OC(B/2)和拉伸后的网片坡长AC在空间上形成直角三角形,见图14。
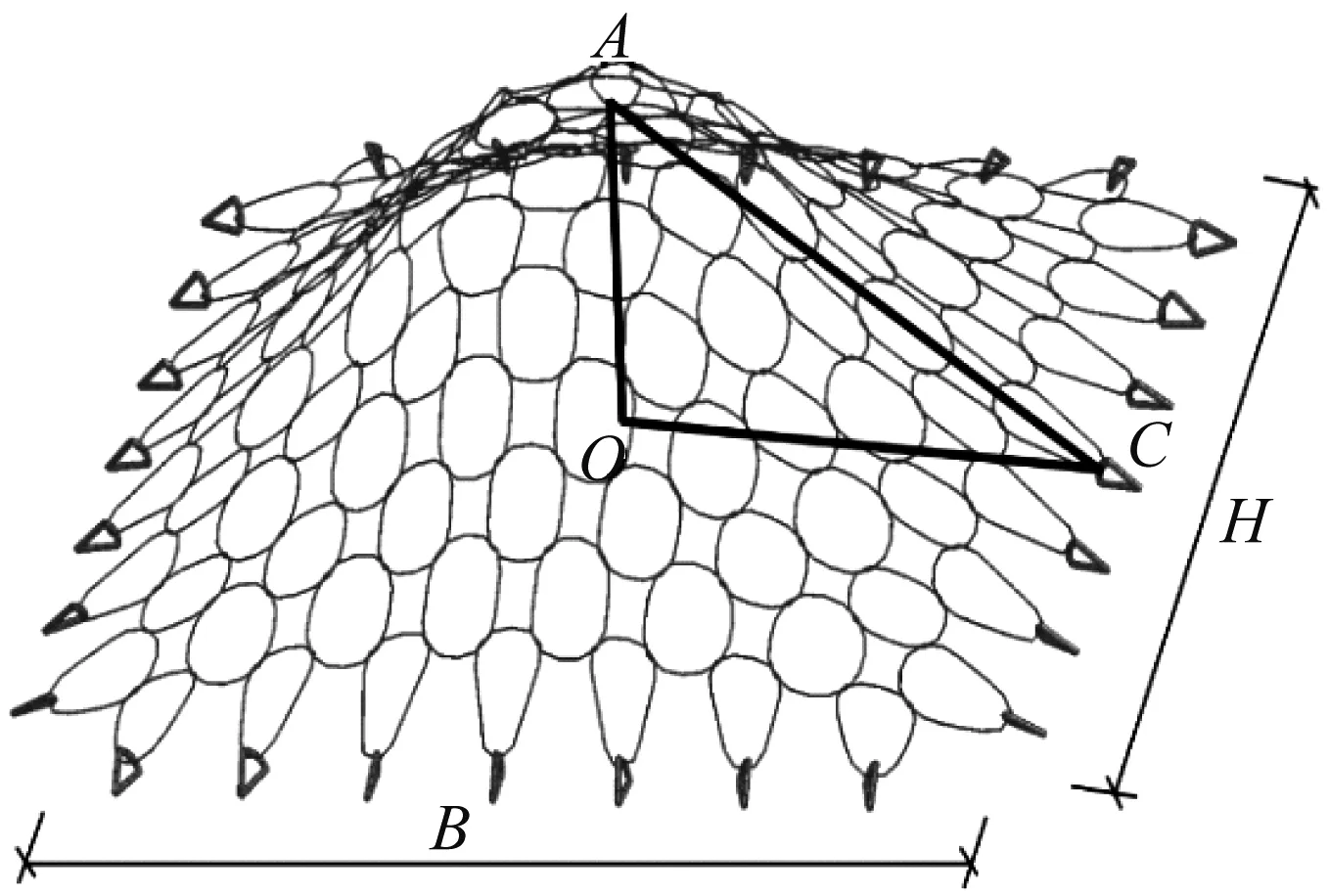
图14 极限拉伸的临界状态
横、纵两个方向任意两圆环间均存在空隙,令空隙间距为圆环直径α倍,因此一排的圆环数m:
(8)
式中:m为圆环数量,m取向上取整数;B为网片宽度;H为网片长度;D为圆环直径;网片达到临界破坏时,圆环从圆形转化为正方形,考虑钢丝的伸长量为圆环直径的β倍,拉伸后的空隙间距为圆环直径的γ倍,则AC长度为
(9)
从而确定极限拉伸位移:
Δmax=OA=
(10)
5.2 顶破力-位移归一化曲线
为了得到网片的整体受力情况,将前述19个模型的顶破力-拉伸位移曲线为拟合数据,各项参数(圆环的缠绕圈数N、圆环直径D、顶破端与环形网的面积比μ和环形网的长宽比)作为自变量,进行多参数曲线归一化拟合,得到归一化公式为
(11)
式中:ζ1、ζ2、ζ3为相关系数
(12)
ζ2=0.2×D2μλN-201.72
(13)
ζ3=-1.23λDμ+0.37N-4.45
(14)
同时需要满足Δ≤Δmax=OA
6 动力冲击验证
为研究归一化公式的通用性和正确性,参照文献[5]的模型试验(图15),试验的环形网尺寸为3.9 m×3.9 m,网型采用R7/3/300。提取文献中的试验数据,采用数值模拟对相同试验参数模型进行落石模拟(冲击后的网片变形图对比如图16),并将圆环直径D=300 m,圆环缠绕圈数N=7,落石与网片面积比μ=0.03,网片长宽比λ=1,考虑网片几何尺寸增大系数为(3.9×3.9/3/3=1.3),动力放大系数取为1.1,代入到式(11)中,得到该网型的归一化曲线公式为

图15 试验模型

图16 冲击后变形图对比
P=0.22e(Δ/205)-4.03
(15)
试验、数值模拟以及归一公式所得的冲击位移和冲击力对比如表4,三种工况下的最大冲击力的标准差为12.50 kN,变异系数为7.33%,最大冲击位移的标准差为20.11 nn,变异系数为1.46%,表明三种工况下冲击力和冲击位移的极值取得了较好的一致性。三种工况下力——位移曲线对比见图17,采用归一化公式计算所的的曲线,介于数值模拟和文献试验结果之间,验证了该归一化公式的有效性。
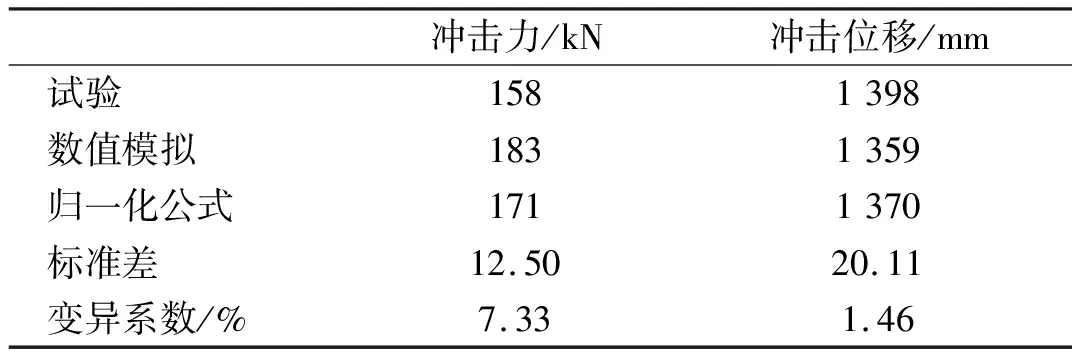
表4 最大冲击力和最大冲击位移对比

图17 力——位移曲线对比
7 结 论
本文结合柔性环形网顶破力学试验和数值模拟,分析了不同参数对环形受力性能的影响,得到以下结论:
(1)柔性环形网平面外顶破受力变形可分为三个阶段:第一阶段顶破力平缓增长,拉伸位移急剧增大;第二阶段顶破力急速增大,网环变形速率减慢;第三阶段,荷载达到顶破力极值,网片破断。
(2)随着圆环缠绕圈数的增多,整体网片的破断力持续线形增大,极限拉伸位移小幅线形减小。随着圆环直径的增加,破断力指数型减小,极限拉伸位移线形增大。随着顶破端与环形网面积的比值的增大,破断力和极限拉伸位移呈幂函数减小。随着环形网长宽比的增大,破断力和极限拉伸位移呈幂函数减小,破断力减小速率更快。
(3)根据试验与数值模拟的结果,提出了环形网片拉伸变形的解析计算方法和顶破力——拉伸位移的相关性方程。采用该方程可快速确定相应网片的破断力和极限拉伸位移,为柔性防护系统环形网单元设计提供了参考。
