考虑驱动和负载状态的三自由度超声电机接触模型研究

李 争，赵 亮，郭 鹏, 于絮泽

(河北科技大学 电气工程学院，石家庄 050018)

超声电机是1980年以来前景较好的一种新型微电机。超声电机通过压电陶瓷的逆压电效应将输入的电能转化为振动机 械能，再通过振动的叠加组合和摩擦力驱动转子[1-4]，它在很多方面优于电磁电机，如：毫秒级响应速度、可断电自锁、大转矩、高精度、抗电磁干扰[5-9]，在微机械、医疗器械、精密加工和航空航天等领域具有广泛应用和广阔的前景[10-14]。

由于超声电机的定子-转子间通过摩擦传递能量，所以其接触面的摩擦特性对超声电机的性能很重要。目前，国内外学者对此做出了很多研究。Zhu[15]提出了一种基于弹性力学和摩擦层形变的接触模型。Duan等[16]提出了压电耦合定子，转子和接触界面之间完全耦合的有限元框架，并分析了有限元法对压电驱动的一般间歇接触问题的不足。Sun等[17]提出了一种定子摩擦层为黏弹性的接触模型，并将该模型与滑块为柔性、定子为刚性的模型比较，结果证明基于该模型的电机将获得更大的失速扭矩和更大耐磨性。蒋春荣等[18]提出了一种摩擦层在定子上、转子为刚性的接触模型。

本文提出了一种对于三定子多自由度超声电机的新型的接触模型。首先，介绍了多自由度超声电机的基本原理和结构；计算得出了压电驱动的转矩公式；引入Hertz接触理论和Mindlin理论分析接触层摩擦力的分布，建立考虑非线性的摩擦界面模型，最后通过转矩公式和摩擦模型得出不同驱动、运动状态下的多自由度超声电机接触面的摩擦力分布以及定子轴与xoy平面的夹角对转矩的影响。

1 多自由度超声电机结构和原理

多自由度超声电机主要由三个环形定子(定子S1、定子S2、定子S3)和一个球形转子组成，三个定子对称分布于球形转子内部，如图1所示。

(a)外部结构

三个定子均由两相空间相位差为π/2的压电陶瓷片组成，其均沿厚度方向极化且相邻压电陶瓷片为相反的极化方式，每个压电陶瓷片长λ/2。对定子施加两相等频、等幅、相位差为π/2的交流电时，两相压电陶瓷上产生的振动经过弹性体放大和叠加后在齿上形成行波，再通过摩擦作用驱动转子旋转。同时由于三个定子不共面，球形转子可以在三个驱动转矩的共同作用下产生任何一个方向的旋转运动，实现电机的三自由度驱动。

多自由度超声电机的连接方式和预压力结构,如图2所示。支撑体、基体和预压力杆材料均为钢材且倾角一致，行波定子通过三个螺栓装置与支撑体上部分的圆盘固定连接，支撑体下部分的圆柱与基体的圆形开孔直径相等且可沿开孔轴向滑动。预压力杆顶端锥形结构与支撑体圆柱部分为刚性接触，底端通过螺栓结构基体底端连接，通过在预压力杆底端螺栓结构可以使预压力杆上下移动，推动支撑体的轴向位移，从而增大或减小行波定子和转子的预压力。由于基体和行波定子空间上均为对称结构，所以三个定子和转子之间的预压力大小保持一致。

图2 预压力结构截面图

对电机定子-转子建立正交坐标系，如图3所示。三个定子在周向均匀分布且轴线与xoy平面夹角为α。由于三个定子角速度矢量的合成矢量可分解到x轴、y轴、z轴，因此电机可以实现三自由度运动。设定子角速度合成矢量为ωt，其在定子轴S1、S2和S3方向的分量分别为ω1、ω2和ω3，表达式为：

图3 超声电机内部结构及坐标系

ωt=ω1u1+ω2u2+ω3u3

(1)

式中，ω1、ω2和ω3为标量，其大小由施加到定子上的激励电压的大小、频率、相位差决定，u1、u2和u3分别为三个定子轴的方向向量，沿球心向外。u1在oxyz坐标系下的表达式为：

u1=[cosα0 sinα]T

(2)

由于u2和u3分别为u1为绕z轴旋转2π/3和4π/3，所以u2和u3经过转换矩阵A02和A03变换后可得，其表达式分别为：

(3)

当球形转子旋转时受到接触面摩擦力的影响，所以超声驱动的模型包括来自3个定子的摩擦力矩与定子的角速度矢量关系。令ω表示球形转子的角速度矢量，其与定子S1的线成ψ1角，如图4所示。

图4 转子相对于定子的角速度和转矩

转子角速度矢量ω的标量为ω。定义定子S1的角速度为ω1，定子S1的接触半径为r。定子和球形转子之间的预压力为P。定子S1和球形转子之间的总转矩T1包括驱动转矩。

Ta1和摩擦转矩Tf1，表示为：

T1=Ta1u1+Tf1uf1

(4)

式中,uf1为摩擦转矩的方向向量。

由于转子角速度可以分解为平行和垂直于定子S1的两部分，所以驱动转矩Ta1由定子S1速度快于转子平行转速而产生的摩擦力决定，摩擦转矩Tf1由定子速度慢于转子相同转向的速度产生的摩擦力和与定子速度方向垂直的转子方向产生的摩擦力驱动。驱动转矩Ta1可表示为：

Ta1=cd(ωS1-ωcosψ1)rP

(5)

摩擦阻力矩Tf1表达式为：

Tf1=-(cdcosψ1+crsinψ1)ωrP

(6)

式中:cd为周向摩擦因数，cr为径向摩擦因数，如图5所示。

图5 径向摩擦因数和周向摩擦因数

uf1在如图4所示坐标系中为周向旋转提供的摩擦阻力和球形转子垂直于定子角速度产生的摩擦阻力矢量和的单位向量，转换到oxyz坐标：

(7)

式中:γ1为定子S1坐标系平面与z轴夹角。

uf2和uf3分析方式与uf1相同，在取值γ2、γ3和ψ2、ψ3的基础上，可表示为：

(8)

式中,ψ1、ψ2、ψ3可以根据电机角速度方向通过几何关系得到。

转子角速度矢量与定子S2、S3轴线的夹角分别为ψ2和ψ3，定子S2和定子S3的转矩T2和T3分析方法与T1相同。

2 三自由度超声电机接触状态分析

三自由度超声电机由三个定子的合成转矩作为输出转矩，因为转矩是摩擦力的函数，且驱动摩擦力和摩擦阻力均垂直于压电定子径向，即其夹角为90°。由转矩-力的关系可知摩擦力F=T/r，因此可通过第二章求得转矩进而得出接触面摩擦力的大小，再通过下述的摩擦模型可得出摩擦力分布。

三自由度超声电机不同的驱动状态接触面摩擦力分布不同，添加负载后电机的运动也状态不同，所以其接触状态分布会改变。电机的运动状态可以分为以下几类：堵转运动；自转运动；偏转运动；带负载运动。

2.1 摩擦模型

由于定子-转子接触面有很多非线性因素，因此假设：

1)电机定子、转子为刚性体；

2)定子表面连续，忽略定子齿槽的影响。

由于定子-转子间接触层径向接触宽度远小于周向接触长度，径向形变可忽略不计，所以可以降维建立二维接触模型，如图6所示。

图6 定子-转子接触模型

通过位移-应变-应力的关系得出预压力可表示为[14]:

(9)

根据摩擦驱动模型，摩擦因数的大小与滚轮和平板的相对速度大小呈线性关系，摩擦力表示为：

τ(x)=cd(ωs-ωr)p

(10)

式中:cd为定子周向摩擦因数，p为接触面垂直方向的压力分布，ωs为压电定子角速度，ωr为转子角速度，可通过实验测量得到。

两个物体受到法向压力P和切向摩擦力F作用，法向压力分布等效为Hertz接触理论，切向摩擦力由Mindlin理论求得，其计算值与处于稳态的弹性物体近似。当弹性安定时，假设接触压力保持不变。

在二维情况下，由Hertz接触理论可知其法向压力分布为：

(11)

式中:p0为法向压力最大值，即p在x=0处的值，a为摩擦层接触长度的1/2。

电机运行过程中，摩擦层处既有摩擦驱动力，也有摩擦阻力，在任意转速下其矢量和最大值都大于相同转速下静摩擦力。由Mindlin理论可得接触面切向力表示为：

(12)

式中:c为实际摩擦力F的函数，表达式为：c/a=[1-(Fmax-F)/2μP]1/2，根据图6，Fmax为定子最大摩擦力，其大小由周向驱动摩擦力和径向摩擦力矢量和决定，实际摩擦力由周向驱动摩擦力、周向摩擦阻力和径向摩擦阻力的矢量和决定，μ为当前速度下的摩擦因数。

2.2 堵转运动

当压电驱动激励施加到电机时，如果电机处于堵转状态，即ω=0，则定子-转子接触层仅有摩擦阻力。此时，其转矩表达式由式(4)～式(6)给出，并且摩擦力分布可以从等式T=F×r和摩擦模型获得。

2.3 多自由度空载运动

通常，有三种方法可以调节电机转速：调压，调频和调相位差。其中，调压的线性相关性最好。

如果对三个压电定子施加同幅、同频、同相位差的交流电压，则三个定子产生幅值相等、速度的大小和方向均相同的行波，并且转矩在空间上对称，电机可实现自转运动。

如果三组激励电压的相位差不相等，则三相定子产生空间上不对称的行波，所以转矩也是不对称的。此时，电机实现偏转运动。其转矩表达式由式(4)～式(6)给出，并且摩擦力分布可以从等式T=F×r和摩擦模型获得。

2.4 带负载运动

负载转矩可分解到三个定子轴方向，与不同的驱动方式产生的转矩叠加等小成定子转矩，当负载转矩与水平面垂直时，其沿三个定子轴方向的大小均为TR/(3sinα)；当负载转矩不与z轴平行时，其分解转矩表示为：

(13)

所以转矩方向不与z轴平行的负载转矩对三个定子接触状态的影响也不相同。压电定子的驱动转矩和阻力转矩由式(4)～式(6)得出，摩擦力分布可由公式T=F×r和摩擦模型得到。

3 三自由度超声电机接触状态计算

在该实验中，为了测量样机在不同驱动和负载条件下的转速，首先用阻抗分析仪(HT2829A，Tonghui，China)分析压电定子在不同驱动频率下的阻抗。阻抗分析仪夹具分别连接样机定子的通电端和接地端，如图7所示，这样可测量出压电定子阻抗和频率的关系，得出定子的谐振频率，实现最大的输出性能以方便测量，其中定子的阻抗-频率关系如图9所示。由于每个定子均有两相压电陶瓷，对这两相压电陶瓷的测量结果是一致的；对于三个定子，由于制作、安装的微小误差导致的不对称，其测试结果也具有微小的偏差，所以分别对三个定子的进行了测试，其谐振频率分别为40.350 kHz、40.360 kHz、40.365 kHz，取其平均值为40.358 kHz。

图7 样机阻抗-相位测量平台

图8 样机性能测试平台

图9 样机的阻抗-频率关系图

然后，通过上位机调整驱动电压的频率到谐振频率，并通过MPU-9250九轴姿态传感器实时记录样机的转速和欧拉角，通过滑轮-线-砝码装置增加负载。实验平台如图8所示。由于通过调压调节压电驱动的输出性能具有最好的线性相关性，测试了压电驱动装置转速-驱动电压幅值的关系，结果如图10所示。从图10中可知，当电压低于450 V时，样机的转速-电压关系近似线性。当驱动电压大于450 V时，转速的增加幅度逐渐降低。

图10 样机转速-电压关系图

为了使结果更加明显，根据以上实验，以下均为样机，电压幅值为400 V、电压频率为40.356 kHz情况下测试的电机转速进行的计算。

3.1 堵转运动

当压电驱动激励应用于三自由度超声电机并且电机处于堵转状态时，由于转子速度为零，定子-转子接触层仅有摩擦阻力，并且由于定子和转子之间的平均转速之差最大，接触层的所以平均摩擦力最高。摩擦力分布,如图11所示。

图11 堵转时接触层摩擦力分布

3.2 自转运动

对三个定子分别施加三组两相等幅、等频和等相位差的电压，由于三相定子空间对称，而且激励电压相同，因此三相合成转矩也关于z轴对称。通过等式(4)～式(6)可得出电机的输出转矩平行于z轴，电机实现围绕z轴的旋转。另外，三个定子-转子的相对速度是相同的，因此其接触状态相同。摩擦力分布,如图12所示。

图12 施加对称激励电压时三相定子接触层摩擦力分布

3.3 偏转运动

将三组不对称激励电压施加到三个定子，此时由压电定子产生的扭矩的大小和方向是不对称的。原型的总输出扭矩不平行于z轴，电机实现偏转运动，偏转方向与原型的总输出扭矩方向一致。当偏转角为θ= 27.4°，φ=22.3°时，三相定子接触层的摩擦分布如图13～15所示。

图13 施加不对称激励电压时定子1接触层摩擦力分布

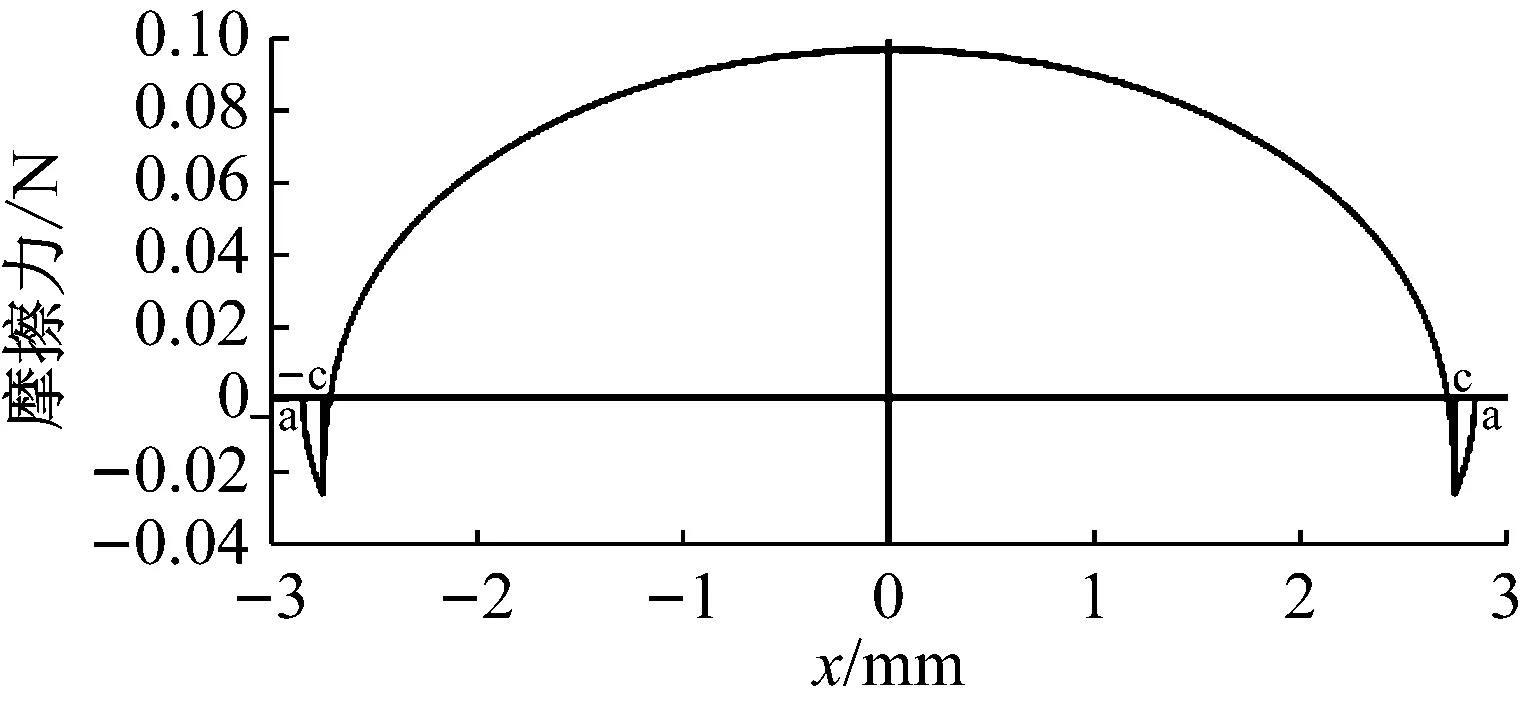
图14 施加不对称激励电压时定子2接触层摩擦力分布

可以直观地从图13～图15中得出，三个定子摩擦力的大小和分布是不同的，并且由于定子S2的旋转方向是-94.32°，所以定子S2的接触表面的摩擦力对于球形转子接近摩擦阻力，降低了电机的输出性能。

图15 施加不对称激励电压时定子3接触层摩擦力分布

3.4 带负载运动

当负载转矩为120 N·mm时，由于负载对电机运动状态的影响，电机的转速降低，但定子的行波速度是恒定的，这导致球形转子和压电的相对速度相较于无负载状态更大，所以定子-转子接触面的摩擦力增大，摩擦力分布,如图16所示。

图16 带负载时定子接触层摩擦力分布

3.5 定子轴与xoy平面夹角对压电自转转矩的影响

电机定子轴线与xoy平面的α夹角选值不同，电机的输出转矩也会随之改变，如图17为三相激励电压相同时不同α值对应的z轴输出转矩。

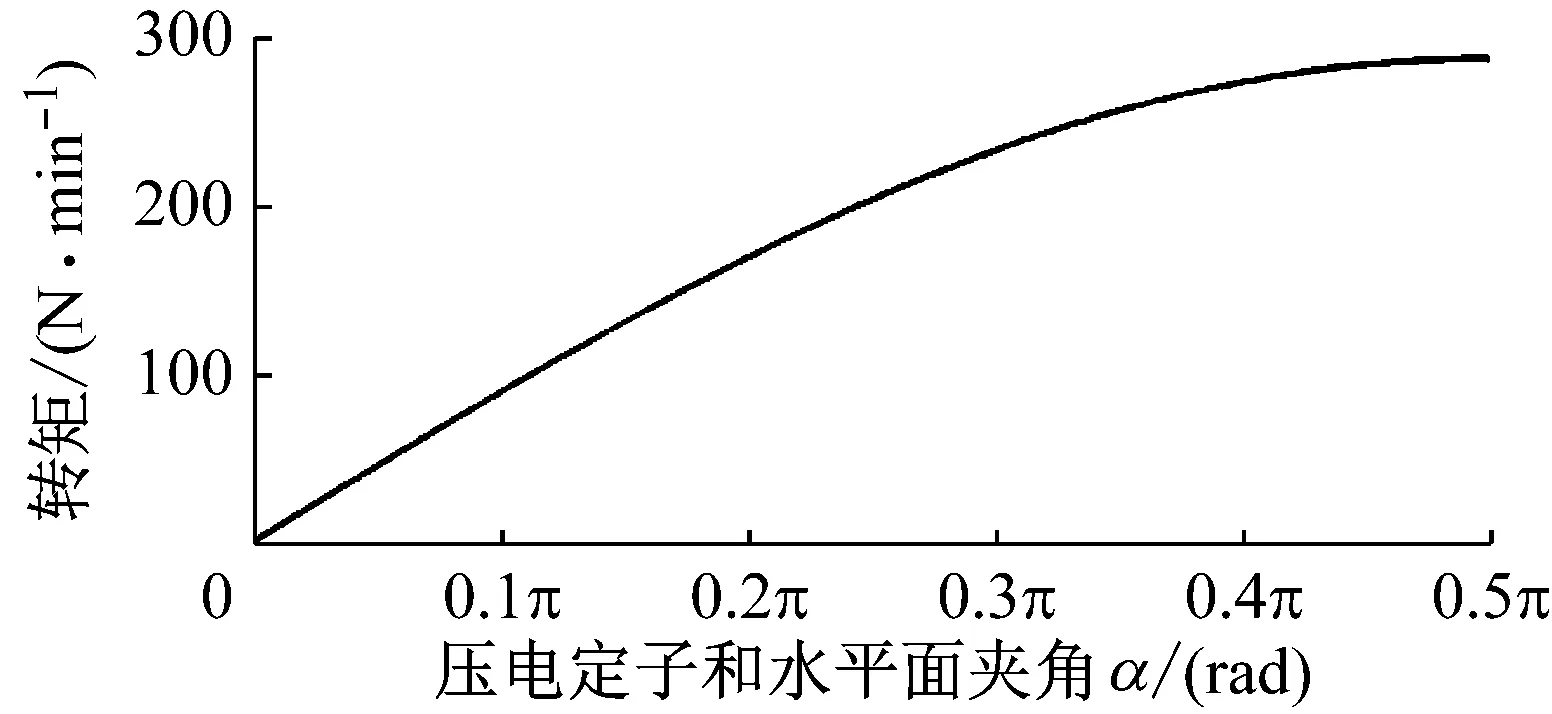
图17 定子轴与xoy平面夹角对压电自转转矩的影响

由图17可知，当α为0时，z轴输出转矩为0，电机不能围绕z轴旋转，此时该电机失去一个自由度，为二自由度电机。α值越大，z轴转矩越大，当在结构允许范围内，α接近极值π/2时，z轴转矩达到最大值。

x轴输出转矩和y轴输出转矩不仅和α角相关，也和三相电压是否相同以及负载转矩方向相关，若三相电压相同且负载方向平行于z轴，则x轴和y轴转矩为0，若电机运行角速度方向不平行于z轴，则x轴转矩和y轴转矩与cosα成正比。

4 结 论

建立压电定子-转子界面接触模型是建立三自由度超声电机耦合系统的动力学模型中的关键之一。三自由度超声电机的驱动状态和负载不同，电机的运动状态和转矩也不相同，三个定子的接触层摩擦力分布通过压电转矩和摩擦擦模型得出，为接触层摩擦界面的优化设计提供了依据。

首先介绍了三自由度超声电机的基本原理和结构；通过解析法得出电机转矩；通过对非弹性体移动接触的分析，并引入Hertz接触理论和Mindlin理论对接触层摩擦力分布进行分析，建立了考虑了非线性部分的摩擦界面模型，最后通过求出的转矩和摩擦模型结合，用Matlab得出不同驱动、运动状态下的三自由度超声电机的接触面摩擦力分布图。

通过对三自由度超声电机转矩的详细分析，可以得出压电驱动转矩会对接触状态产生影响，压电驱动转矩由定子角速度、球形转子角速度矢量和负载情况决定，再根据摩擦模型得出最终的接触状态，且定子与球形转子的相对速度与摩擦力成正比，验证了三自由超声度的可行性，分析了不同驱动状态、负载下接触层摩擦力的分布，对认识定子-转子接触机理、进一步优化摩擦界面提供了支持。