航天器太阳帆板多自由度减振装置设计
2021-02-06朱仕尧雷勇军
朱仕尧,雷勇军,郭 欣
(国防科技大学 空天科学学院,长沙 410073)
现代航天器上外伸的太阳帆板会引起两类振动问题。①残余振动:太阳帆板具有频率低、阻尼小等特点,导致其在航天器姿态调整和进出阴影产生的振动响应需要较长时间衰减,影响航天器姿态稳定时间和快速响应能力[1];②驱动扰动:为尽可能多获取能量,太阳帆板需要不断旋转以持续面向太阳,由此引起的连续扰动会影响高精度航天器指向精度和敏感设备的动态环境[2]。
一方面,残余振动属于自由振动问题,发生在帆板面外方向,主要由弯曲模态振动引起。抑制残余振动的目的是为了加快衰减速度,缩短振动稳定所需的时间,可以从被动和主动两个方面开展减振研究。哈勃空间望远镜阻尼器[3]是太阳帆板被动减振方法的典型应用,其利用阻尼层剪切变形耗散振动能量。刘超等[4]用聚合物阻尼材料替代阻尼器中的黏弹性阻尼材料,并证明模态阻尼比随温度升高而增大。Jia等[5-7]分别研究了平台式、斜杆支撑式和质量调谐式太阳帆板阻尼器设计。在主动减振方面,Weck等[8-12]以嵌入太阳帆板支架和基板内部形状记忆合金丝或粘贴于基板表面的压电陶瓷片为作动器,采用分散化控制、线性最优控制、非线性黄金分割自适应控制或混合灵敏度H∞鲁棒控制等理论设计控制率,提高太阳帆板振动衰减速率。
另一方面,驱动扰动属于强迫振动问题,发生在帆板旋转运动方向,主要由驱动装置驱动运动和太阳帆板扭转模态耦合引起。抑制驱动扰动的目的是通过避免结构共振,降低扰动幅度。目前对太阳帆板驱动扰动的抑制主要集中在改进驱动装置运动平稳性,减小输出力矩的波动幅度。Chen等[13-14]讨论了太阳帆板步进驱动扰动特征。Zhou等[15]引入输入成形的驱动指令以改善驱动指向精度。Atlas等[16]采用一种修正的正弦驱动指令,减小系统误差的影响,提高驱动稳定性。Zhu等[17-19]从力矩平衡方程出发,在参考电流中引入补偿项,抵消谐波扰动成分,提高驱动运动稳定性。
综上,残余振动和驱动扰动属于不同的振动类别,发生在不同的自由度,且涉及不同的振动模态,上述研究中将太阳帆板驱动系统(Solar Array Drive System, SADS)的减振问题单独考虑残余振动或驱动扰动问题。这无疑简化了驱动系统减振问题的难度,但较少涉及驱动系统动力特性的系统性改进。为此,本文提出了在太阳帆板与驱动装置之间设置一种刚度可调的多自由度减振装置(Multi-degree-of-freedom Vibration Reduction Device, MVRD),以改善结构系统多种振动模式下的动力学特性,同时削弱上述两种振动干扰(如图1所示)。首先基于虚功原理和混合坐标描述,对含减振装置的驱动系统进行动力学建模;然后系统分析减振装置等效参数对扭转和弯曲模态动力学特性的影响规律。在此基础上,设计减振装置原理样机,通过驱动扰动特性试验和模态参数测试试验,验证了减振装置对两类减振问题的有效性。
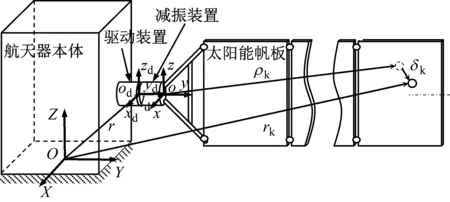
图1 太阳帆板驱动系统组成示意图
1 驱动系统动力学建模
1.1 基本假设
坐标体系定义如图1所示。基本假设如下:①航天器本体:本体结构为刚性体,且约束平动和转动位移;②驱动装置:太阳帆板转速很慢,短时间内可认为驱动装置转角为小量;③减振装置:相对于展开状态太阳帆板,减振装置质量和结构尺寸为小量,仅体现其刚度和阻尼特性;④太阳帆板:小变形情况下,忽略太阳帆板材料参数和展开锁定装置连接刚度等非线性因素。
1.2 动力学描述
太阳帆板驱动系统虚功主要由惯性力、外力、内力、约束力以及阻尼力引起。惯性力虚功δWI由驱动装置和太阳帆板两部分引入,具体可以表示为
(1)
式中:Mm和Jm为驱动装置转动部件的质量和转动惯量矩阵;r为驱动装置对本体系原点的矢径;θd和ωd为驱动装置转角和转速;mk、ak和rk为帆板k节点的质量、加速度及矢径;M、S、J、P和H分别为太阳帆板的质量、静矩、惯性矩、模态动量和模态角动量矩阵;A和Ad为太阳帆板和驱动装置到本体坐标系的转换矩阵;Ads和Asd为减振装置和太阳帆板随体坐标系之间的转换矩阵;η为太阳帆板模态坐标;Δd和φd为减振装置平动和转动方向变形向量。
驱动系统的弹性势能包括太阳帆板模态变形势能以及减振装置的平动和转动变形势能。根据功能转换原理,内力虚功δWN等于虚应变能的相反数
δWN=-δU=-(δΔdKrΔd+δφdKθφd)-δηTΛη
(2)
式中:Kr和Kθ为减振装置的平动和转动等效刚度矩阵。类似地,阻尼力虚功δWD具体可以表示为
(3)
式中:Dr和Dθ为减振装置的平动和转动等效阻尼矩阵。
在不考虑空间环境干扰和航天器本体激扰情况下,驱动力矩Tl是作用在太阳帆板上的唯一外力,对应的虚位移只发生在驱动方向。因此,外力虚功δWE表示为
δWE=T·δθ=δθTT
(4)
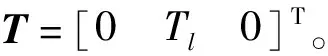

(5)
式中:θ|1和θ|3为θ的第一和三分量,ρo为帆板系原点到本体系原点距离。取虚位移为δq,则式(5)可整理为
(6)
式中:Cq是C(q,t)的雅可比矩阵,其中各参数矩阵为
(7)
引入拉格朗日乘子λ后,约束力虚功δWC表示为
(8)

1.3 模型组集
对太阳帆板驱动系统应用虚功原理
δWI+δWE+δWN+δWC+δWD=0
(9)
将式(1)~式(4)和式(8)代入式(9)并整理得到
由于短时间内的驱动装置转角θd和减振装置扭转变形φd均为小量,则坐标转换矩阵取值接近单位阵。因此驱动系统动力学方程表示为如下形式
(10)
式中:左边三项分别为广义质量、阻尼和刚度矩阵。根据式(5)中的运动约束关系,式(10)可整理为
(11)
式中:θl和ωl为太阳帆板转角和转速;Jm2和J2为转动惯量在驱动方向分量;|2h和|2l表示第二行或列分量。
2 减振装置影响分析
本节在对所建立模型进行合理等效基础上,重点分析减振装置结构参数对驱动系统扭转和弯曲模态的影响规律,为减振装置结构设计提供设计依据。
2.1 动力学特性等效分析模型
根据文献[20]可知,驱动力矩Tl可近似为
(12)
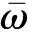
将式(12)代入式(11),并整理为
(13)
式中各项表达式为
式(13)中减振装置对系统动力学特性影响体现为六自由度弹性阻尼单元,而驱动装置对系统动力学特性的影响表现为扭转弹性边界条件,如图2所示。
以某型卫星太阳帆板结构为例进行影响分析,其质量为21.6 kg,几何尺寸和材料如图2所示。固支边界下前三阶弯曲固有频率分别为0.396 Hz,2.176 Hz和5.148 Hz;前三阶扭转模态固有频率分别为1.492 Hz,5.237 Hz和10.004 Hz;振型见图3,其中不同填充颜色代表振动方向相反。

图2 驱动系统动力学特性等效模型

(a)一阶弯曲
2.2 扭转模态动力特性影响分析
将驱动系统扭转模态动力学方程从式(13)中分离出来进行求解,然后分析减振装置结构系数对驱动系统模态动力学特性的影响。
2.2.1 特征值问题求解
扭转模态动力学方程可从式(13)中分离出来:
进行拉普拉斯变换后得到
(MTs2+DTs+KT)qT(s)=0
(14)
由此将扭转模态特征值问题转换为关于式(14)系数矩阵的代数方程求解问题:
det[MTs2+DTs+KT]=[(J2s2+Dds+Kd)×
(15)
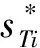
(16)
2.2.2 扭转模态参数影响分析
从扭转模态动力学方程不难发现:减振装置绕y轴刚度和阻尼系数对系统扭转模态动力学特性具有重要影响。图4为fT和ξT随减振装置绕y轴等效刚度的变化曲线,其中减振装置等效阻尼系数取1.5 Nms/rad。fT仅在特定刚度范围内随减振装置刚度系数升高而增大,分别由0.039 Hz、2.280 Hz和6.810 Hz提高到0.748 Hz、4.645 Hz和12.990 Hz,而在其余区间内基本保持不变。ξT1随减振装置刚度增大而逐渐减小,并最终稳定在0.004;ξT2和ξT3在等效刚度较小和较大的区间内均保持不变,仅在中间特定刚度范围内随刚度增大而逐渐减小。图5为fT和ξT随减振装置绕y轴等效阻尼的变化曲线,其中减振装置等效刚度为100 Nm/rad。fT对减振装置阻尼参数并不敏感,基本保持不变。ξT随减振装置阻尼参数增大而逐渐增大,ξT2和ξT3的变化幅度明显大于ξT1,分别可达到0.085和0.160。

图4 减振装置绕y轴刚度与扭转模态参数关系曲线

图5 减振装置绕y轴阻尼与扭转模态参数关系曲线
2.3 弯曲模态动力特性影响分析
2.3.1 特征值问题求解
将弯曲模态动力学方程从式(13)中分离出来
通过拉普拉斯变换可得频域方程
(MBs2+DBs+KB)qB(s)=0
(17)
类似地,将弯曲模态特征值问题转换为关于式(17)系数矩阵的代数方程问题:
det[MBs2+DBs+KB]=
(18)
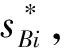
2.3.2 弯曲模态参数影响分析
由动力学方程不难发现:减振装置沿x轴和绕z轴方向上的刚度和阻尼分量会对系统弯曲模态产生重要影响。图6给出绕z轴刚度分量对弯曲模态动力学参数的影响关系。在不同刚度范围内,前三阶固有频率分别从0.005 Hz、0.194 Hz和0.836 Hz明显增大到0.099 Hz、0.268 Hz和1.313 Hz,其余刚度范围内均达到稳定。随着减振装置刚度参数的增大,ξB1逐渐减小。ξB1在刚度系数为0.1 Nm/rad时取得最大值为0.26,随着减振装置刚度参数的增大而逐渐减小,并最终稳定在0.039;刚度系数较小时,ξB2和ξB3平缓变化,并在特定刚度范围内逐渐减小,在高刚度范围内达到稳定。图7给出绕z轴阻尼分量对弯曲模态动力学参数的影响关系。前三阶固有频率在所研究阻尼范围内基本保持不变,说明其对减振装置的阻尼系数并不敏感。但前三阶模态阻尼比随减振装置阻尼系数的增大而增大,且增大速率也在逐渐增大。ξB3增长最明显,而ξB2增长最慢。

图6 减振装置绕z轴刚度与弯曲模态参数关系曲线

图7 减振装置绕z轴阻尼与弯曲模态参数关系曲线
图8和图9分别给出了沿x轴刚度和阻尼分量对弯曲模态动力学参数的影响关系。前三阶固有频率随x轴刚度的变化趋势与绕z轴刚度的变化趋势基本相同,仅变化幅度更为明显。在减振装置刚度为0.1 Nm/rad时,ξB1取得最大值0.49,然后随刚度增加而逐渐减小,直到40 Nm/rad刚度系数趋于稳定。刚度系数相对较小时,ξB2和ξB3平缓变化,而后随着刚度增大而明显减小,并最终趋于稳定。固有频率对减振装置x轴阻尼分量不敏感,在研究范围内的相对变化小于2%。前三阶模态阻尼比随减振装置沿x轴阻尼分量的增大而增大,且增大率也具有相同的变化趋势;其中ξB2最大(可达0.865),ξB1最小(仅为0.052)。
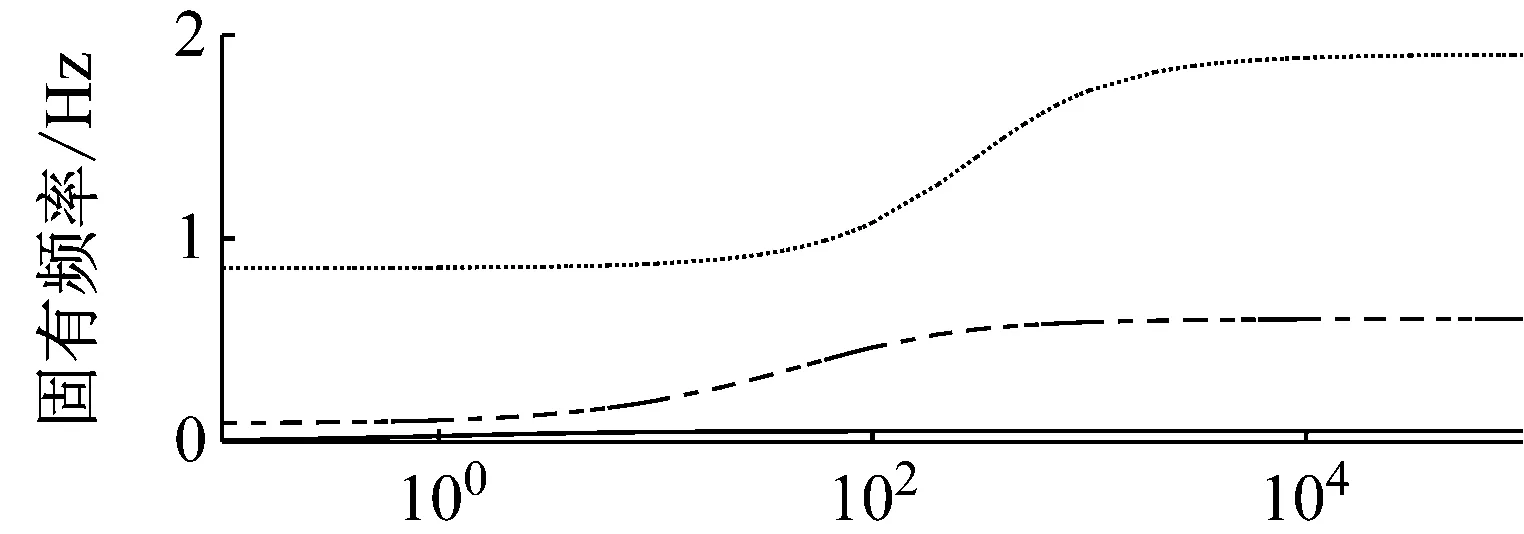
图8 减振装置沿x轴刚度与弯曲模态参数关系曲线

图9 减振装置沿x轴阻尼与弯曲模态参数关系曲线
3 减振装置结构设计
通过合理的减振装置结构设计,可以全面抑制驱动扰动和剩余振动。为便于验证减振装置对太阳帆板一阶弯曲和一阶扭转振动的抑制效果,且考虑到试验验证的可行性,选用包含1个支架和1块基板构成的太阳帆板结构为减振对象,其中部件尺寸和材料如图2所示。结构总质量为14 kg,扭转转动惯量11.74 kg·m2,固支边界一阶弯曲和扭转频率分别为0.787 Hz和0.635 Hz。一方面,根据表2所列驱动装置参数,谐波激励频率为0.21 Hz的整数倍[20];而实际驱动系统的第一扭转固有频率为0.635 Hz,非常接近三次谐波激励频率0.63 Hz。因此,调整第一扭转固有频率有利于降低共振响应。另一方面,弯曲模态的衰减时间与模态阻尼比固有频率均成负相关关系,因此应增大模态阻尼,并尽量避免减小相关固有频率,可以加速残余振动的衰减。
为便于调整等效结构参数,减振装置结构形式相对简单。如图10(a)所示,减振装置主要由高刚度中轴和高损耗因子阻尼环同轴安装而成。图10(b)为采用铝合金材料的中轴结构,其通过上下连接界面分别与顶盖和底盖螺栓连接。中轴为可以更换的部件,通过选用不同中轴截面形状改变减振装置整体刚度特性,例如十字形截面,因其设计参数更多,便于灵活调整各方向刚度分量。图10(c)为采用硅橡胶高分子阻尼材料的阻尼环结构,通过环向均匀布局,尽量增大其分布面积,提高减振装置的阻尼系数。该构型可以保证太阳帆板在发生轴向扭转振动时,阻尼环各部分均发生明显的结构变形,有利于提高阻尼器的等效阻尼参数。顶盖和底盖结构与中轴和阻尼环连接为整体,并在中心开设通孔,便于中轴替换;内表面平整,便于与阻尼环粘接或共固化连接;外表面按安装界面设螺纹孔,用于与驱动装置和太阳帆板连接。

(a)实物图
经反复调整后,确定中轴长度为30 mm;十字界面各边形状相同,单边长为8 mm,单边厚为2 mm;阻尼环内外直径分别为150 mm和110 mm,整体质量为1.169 kg,外包络为Φ156 mm×56 mm。分别在安装减振装置前后进行复模态分析和扰动特性分析,结果见表1和图11。安装减振装置后,一阶扭转固有频率为0.555 Hz,与扰动频率明显错开,对应的模态阻尼比提高491.04%;扰动力矩波动幅度由0.456 Nm降至0.293 Nm,减少35.74%;一阶弯曲模态阻尼比可提高十倍以上,但固有频率仅能降低19.70%,可以计算一阶弯曲模态99%振幅衰减时间从225.9 s大幅降低至24.2 s。

表1 驱动系统复模态分析结果

图11 驱动系统扰动力矩仿真分析结果
4 减振效果验证
在试验室环境中进行了扰动特性和模态特性测试试验,以评价减振装置对太阳帆板轴向驱动扰动和弯曲残余振动的抑制效果。
4.1 扰动特性试验
4.1.1 试验系统
所搭建的模拟太阳帆板驱动系统包括:驱动装置、柔性附件以及减振装置(如图12所示)。驱动装置为低轨直接驱动型SADA(参数见表2);柔性附件由两块构型相同(尺寸为1 630 mm×400 mm×5 mm)的铝合金薄板组成,其与太阳帆板满足转动惯量等效(11.8 kg·m2)和扭转振动基频等效(0.8 Hz)。为抵消柔性附件对驱动装置轴承的压力,在转动轴线方向配备龙门吊和吊装组件以卸载重力。

图12 驱动系统扰动特性测试系统

表2 太阳帆板驱动装置参数
测试系统由Kistler六自由度测力平台、Polytec激光测振仪(包括前置端和后置端)、信号放大器、数据采集器、SADA外置驱动器、计算机及分析软件等组成,如图12所示。测力平台与SADA通过转接工装固定连接,以测量驱动扰动;激光测振仪直接测量激光柔性附件运动速度变化。测量结果分别经过信号放大器和测振仪后置端进行处理,并通过数据采集器传递给计算机。SADA外置驱动器用于产生指定的脉冲信号,控制驱动装置以0.063 5°/s匀速转动。
4.1.2 结果分析
图13给出了匀速驱动指令下达后,驱动系统稳定驱动段扰动力矩时间历程和频谱分布曲线。扰动力矩具有周期性波动特点,具体表现为主要低频波动频率和若干小幅高频波动频率的叠加;频谱分布曲线中均包含一个明显的低频峰值,安装前后频谱峰值对应频率分别为0.625 Hz和0.563 Hz;安装前的波动幅度和频谱峰值均明显高于减振装置安装后。

(a)时间历程
进一步通过图11和图13(a)对比不难发现:分析结果与试验数据一致性较好,扰动力矩主要波动频率基本一致,扰动幅度偏差在17%以内(仿真0.456 Nm,试验0.552 Nm),其主要由试验测得的高频扰动成分引入。表3给出了稳态扰动力矩波动幅度和均方差、平均转速和系统基频数据。对比相同测试状态下的①~③数据可发现:试验结果的重复性良好。安装减振装置前后的扰动力矩波动幅度平均值相对减小41.61%,力矩均方差降低53.48%。这是由于减振方案的实施,一方面调整了系统一阶固有频率,使其降低至0.563 Hz,偏离了激扰频率,减小了系统共振响应;另一方面系统模态阻尼比增加后,在一定程度上减小了柔性附件振幅,从而实现减小系统扰动的目的。
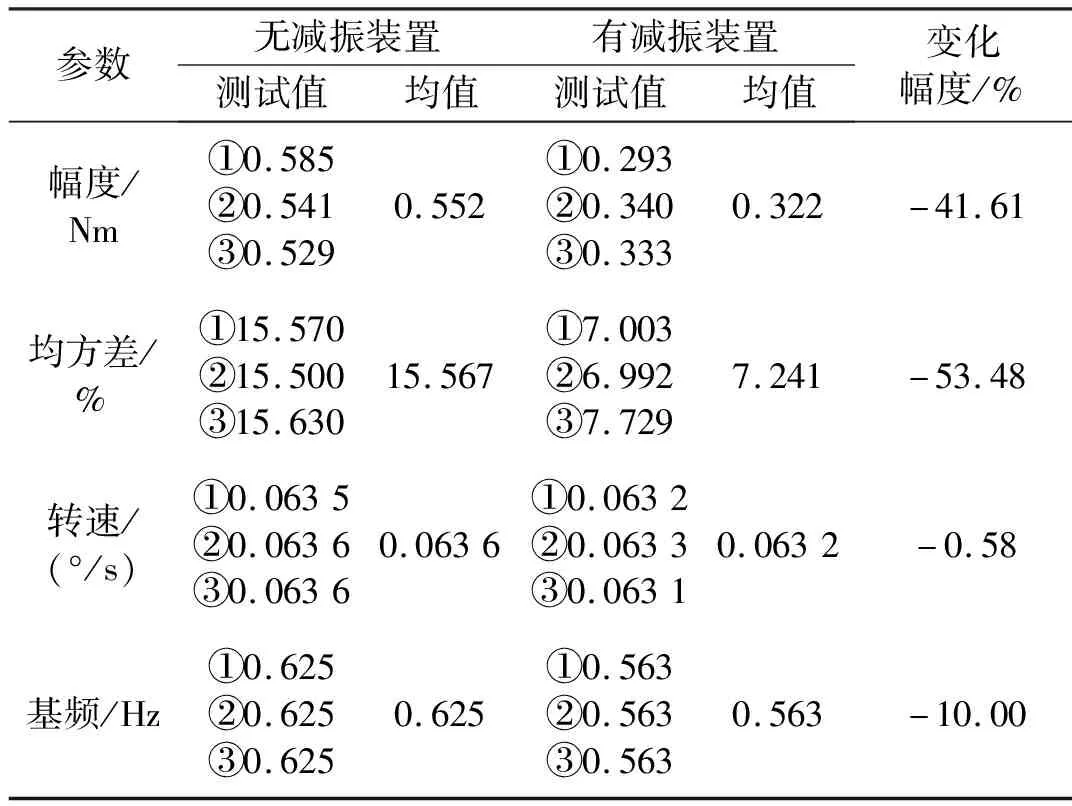
表3 驱动系统扰动特性试验结果
4.2 弯曲模态试验
4.2.1 试验系统
由于驱动装置在非驱动方向可以近似为刚体,因此试验对象仅由减振装置和太阳帆板组成。太阳帆板结构和材料特性如第3章所述,其由重力卸荷装置悬吊,消除重力的影响。减振装置安装在支架和墙面之间。由于本试验是在大气环境中进行,因此大气阻尼效应影响不可避免。测试系统由电磁激励器、力传感器、加速度传感器、电荷放大器、数据采集系统、计算机以及模态测试分析软件等组成,如图14所示。

图14 太阳帆板模态特性测试系统
模态试验采用单点力激励和多点加速度测量方式,其中激励点位于支架横梁上,测点分布在支架和基板表面。模态分析软件通过电荷放大器将0~12.5 Hz频段随机激励信号输出至电磁激励器,数据采集器以400 Hz采样频率采集加速度测点响应,传输给计算机后,分析软件后采用频域辨识方法进行模态辨识,频率辨识分辨率为62.5 mHz。
4.2.2 结果分析
获取的一阶弯曲模态的固有频率和模态阻尼比如表4所示。与表1给出的分析结果对比不难发现:分析与试验测得的固有频率非常接近(分析0.787 Hz,试验0.765 Hz),相对偏差小于3%;由于测试过程中存在空气阻尼,因此测试模态阻尼数据与分析结果的取值存在偏差,但是模态阻尼的变化趋势相同。安装减振装置后,模态阻尼比由3.202%(含空气阻尼)显著增加到8.878%(含空气阻尼),其中减振装置的作用使模态阻尼增加了177%,说明减振装置对太阳帆板的阻尼贡献很大;固有频率从0.765 Hz降至0.63 Hz,仅降低约18%。对比同种测试状态下的①~③数据可以发现:模态试验结果具有良好的重复性。安装减振装置前后的太阳帆板99%振幅衰减时间分别为29.893 s和13.103 s,相对减少56.17%。测试所得模态形状如图15所示,其中模态位移均沿太阳帆板的展开方向逐渐增大,最大位移出现在帆板外缘。
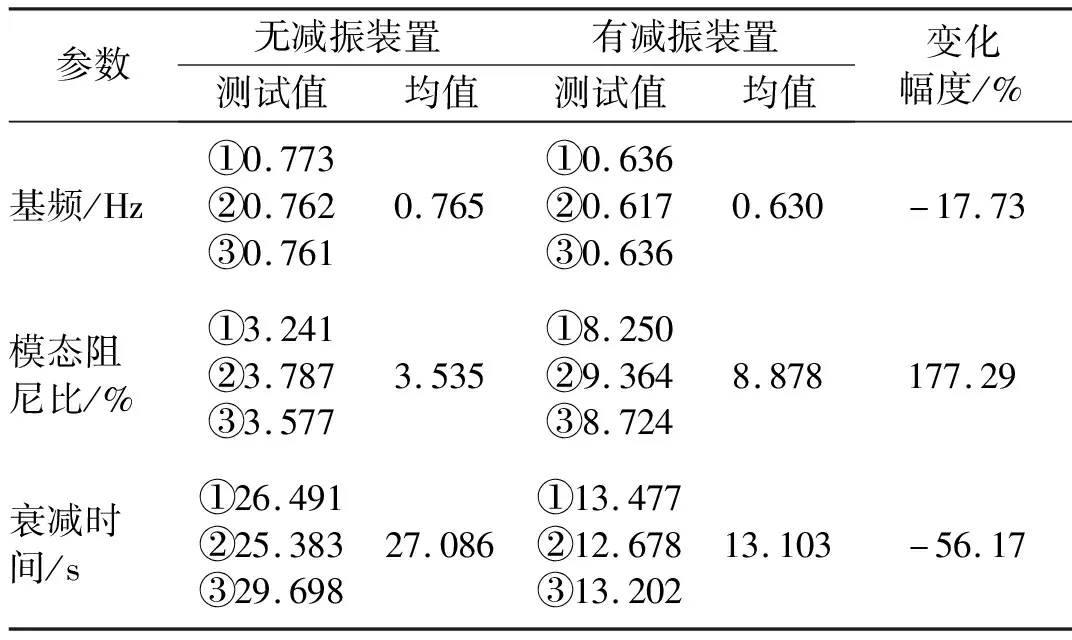
表4 驱动系统模态试验结果

(a)无减振装置
5 结 论
太阳帆板驱动系统的驱动扰动和残余振动属于不同的振动类别,发生在不同的振动方向,涉及不同的振动模态。为了系统抑制这两种振动,本文合理设计了一种安装于太阳帆板和驱动装置之间的多自由度减振装置,通过理论建模、影响分析、结构设计和性能验证,得到主要结论如下:
(1)该减振装置由可更换的中心轴和固定的阻尼环组成,可以在调节固有频率的同时增加系统阻尼。
(2)减振装置的等效刚度仅在特性刚度区间内对驱动系统固有频率影响显著,因此应慎重选择,以使扭转模态固有频率错开驱动扰动激扰频率,避免共振。
(3)减振装置的等效阻尼与系统模态阻尼比呈正相关关系,因此在减振装置的结构设计中建议采用损耗系数高的阻尼材料以加速帆板残余振动衰减。
(4)通过理论和试验方式验证,减振装置对两类振动问题均取得了较好的抑制效果,其中驱动扰动幅值衰减40%以上,99%残余振动衰减时间减少了56%以上。
