基于分离涡方法的台北101大厦流固耦合风致响应分析
2021-02-06卢春玲刘宇杰陈锦焜李秋胜
卢春玲,刘宇杰,陈锦焜,李秋胜
(1.桂林理工大学 土木与建筑工程学院,桂林 541004;2.广西岩土力学与工程重点实验室,桂林 541004;3.桂林理工大学 广西有色金属隐伏矿床勘查及材料开发协同创新中心,桂林 541004;4.中南大学 土木工程学院,长沙 410082)
流固耦合指的是可变形体在风流场中,由于风载荷作用产生变形,而结构变形又反过来作用于风流场,使风流场产生重分布,导致流体对固体作用的荷载大小和分布发生变化。它研究的是流体与固体之间的相互作用。对于阻尼低,自振频率低的超高层建筑物而言,这种流固耦合效应更加明显。近年来,随着计算技术的不断提高,流固耦合相关理论与应用也得到了极大的发展,国内外学术界已经意识到流固耦合效应对建筑结构的抗风稳定性有不可忽视的影响[1-5]。在对建筑结构进行流固耦合相关研究中,对进行流场分析时采用分离涡(Detached Eddy Simulation,DES)算法是一种较为新型的数值模拟方法,相比于目前较常用的大涡模拟方法(Large Eddy Simulation, LES),分离涡模型能在保持精度的前提下有效降低计算量。目前,采用分离涡算法对高层建筑进行流固耦合的研究在国外已有进行[6-7]。本文应用分离涡模拟并结合一种新的可满足大气边界层中风场特性的湍流脉动速度生成方法——离散再合成的随机湍流生成法(DSRFG)[8]模拟非稳态边界层湍流风场。以复杂超高层建筑台北101大厦为对象,对该超高层建筑进行建筑表面风压分布与周围流场分布的数值模拟,模拟得到台北101大厦刚体模型周围的风流场及作用于其上的风荷载时程数据,然后将模型表面风荷载时程施加在超高层建筑有限元模型上,获得未考虑流固耦合效应的结构风致响应分析结果。同时基于WORKBENCH平台构建有限元模型,采用考虑双向流固耦合的方法对超高层建筑模型进行模拟计算,将计算结果与现场实测以及风洞试验的相应数据进行对比,以对该数值模拟方法的实用性和准确性进行检验。同时将考虑与未考虑流固耦合的计算结果进行对比,分析流固耦合效应对101大厦风致响应及结构周围流场分布特性的影响。
1 风洞试验
台北101大厦高频天平测力风洞试验是由Rowan Williams Davies&Irwin Inc.(RWDI)于安大略圭尔夫市的风洞实验室进行的。台北101大厦模型采用与建筑物的几何外形相似的刚性模型,模型缩尺比为1∶500,如图1所示。在RWDI 4.9 m×2.4 m的边界层风洞中,考虑主体建筑600 m半径范围内所有主要建筑物,设定风速采用经过实际风速折减后的试验风速,采用高频天平对台北101大厦的刚性缩尺模型进行测力试验。风洞试验测得湍流强度剖面,见图2。

图1 台北101大厦风洞试验模型
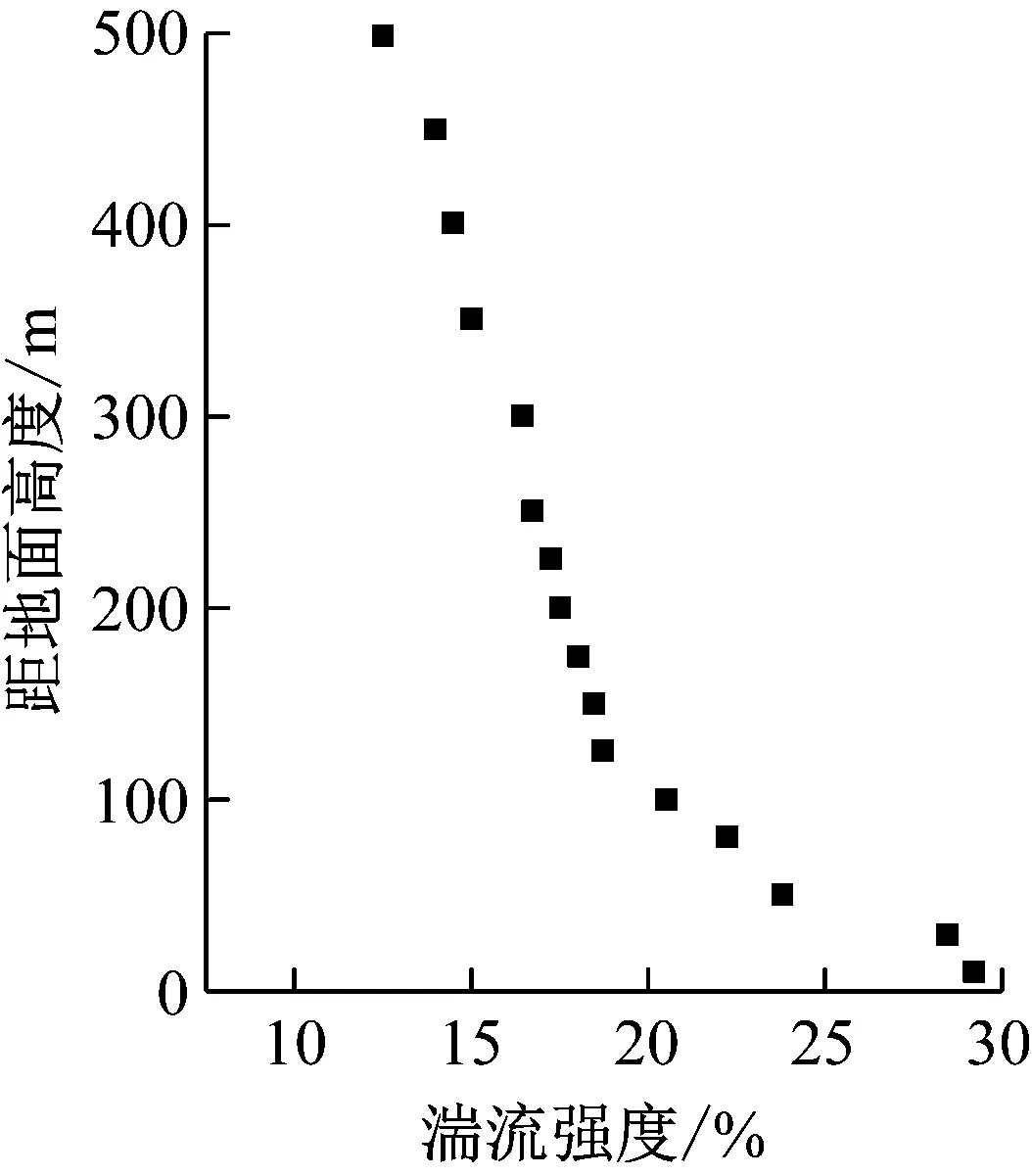
图2 风洞试验湍流强度剖面
2 大厦振动监控系统
台北101大厦动力特性,如自振频率、模态及阻尼比等数据,均来源于在台北101大厦上安装的由传感器和数据采集处理系统组成的振动监测系统。该传感器系统包括30个加速传感器,分别安装在大厦的-5 th(地下室),1 st,36 th,60 th,89 th和101 st层,如图3(a)所示。加速度传感器在大厦平面上的布置如图3(b)所示。用于对比分析的现场实测数据是由采样频率为200 Hz的数据采集系统从2005年8月到2008年5月期间,三次台风作用和一次地震作用下采集得到。

(a)传感器立面布置图
3 数值模拟方法
本文对台北101大楼进行考虑与未考虑流固耦合数值风洞模拟。对未考虑流固耦合的数值风洞,首先建立刚性模型与ANSYS有限元模型,运用fluent软件计算并提取刚性模型表面风压时程,施加在ANSYS有限元模型中获取其风致响应。对考虑流固耦合的数值风洞,则基于结构动力学特性相似原理和workbench平台,建立外形与刚性模型相同,并具有与ANSYS有限元模型相同质量、体积、振型与阻尼比的workbench有限元模型,依靠流固耦合模块直接计算得到其风致响应。
3.1 计算模型及网格划分
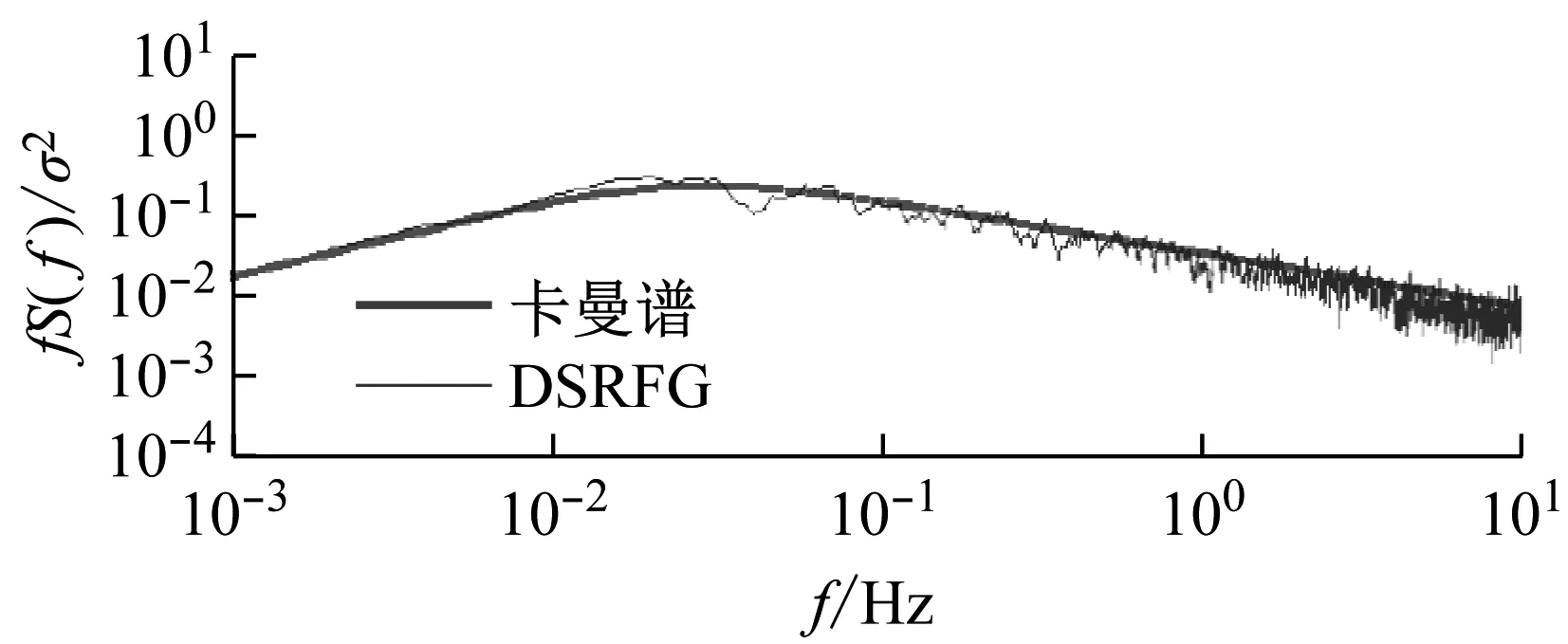
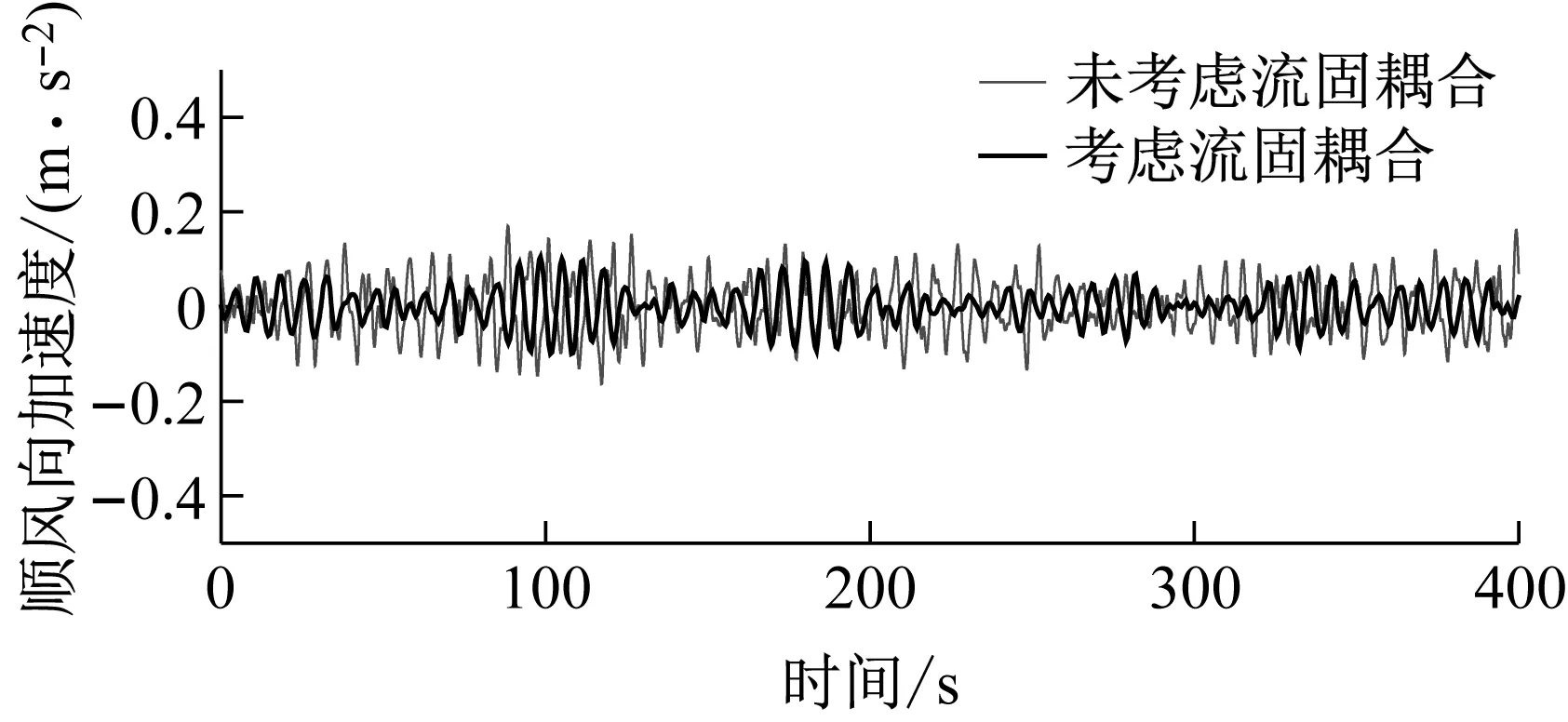
数值风洞计算域见图4(a),在顺风向(X轴方向)的长度为32Db(-9 (1) 经计算流域与模型满足阻塞率小于3%的要求。 本文对计算域中的流体和固体区域网格分别进行划分。对于流体区域,不考虑流固耦合的刚体模型流场采用混合网格划分,网格总数量320万左右,网格划分方式见图4(b)。考虑流固耦合的有限元模型流场采用非结构化网格进行划分,网格数量313万左右。 对于建筑实体部分,未考虑流固耦合的台北101大楼有限元模型通过有限元软件ANSYS建立,分别使用梁单元BEAM188、壳单元SHELL181、杆单元LINK8以及质量单元MASS21构建全尺寸主体结构,并忽略建筑围护结构,大厦的三维有限元模型共计20 532个梁单元,24 048个板单元, 以及3 496个杆单元。ANSYS有限元模型如图4(d)所示。考虑流固耦合的建筑有限元模型基于Workbench平台建立,为便于流体与固体之间耦合面的建立,并在保留建筑模态特性的同时提高计算效率,将建筑模型构建为均质等效模型。建筑单元类型为solid186,单元总数约32万。建筑物整体质量为2.391×108kg,模型体积为1.039×106m3,故材料密度取为230.12 kg/m3;弹性模量取为1.3×109Pa,泊松比取为0.2。 (a)数值风洞计算域整体尺寸 对于流体计算域,刚性模型与弹性模型均采用分离涡模拟的数值模拟方法并采用相同的边界条件。采用作者提出的一种新的湍流入口生成方法-DSRFG方法。速度入口处平均风速沿高度的变化服从指数率,计算公式为 (2) 式中:v、v0为任意高度与标准参考高度处的平均风速(m/s);z、z0为任意高度与标准参考高度(m);α为地面粗糙度指数,取值0.15。文中z0=10 m,10 m高度处50年重现期平均风速v0为43.27 m/s。 基于Shiau[9]在台湾基隆港的观测塔测(距离台北北部约20 km)得的26 m高度处的强风(台风)数据的结果确定台北101大厦入口处的湍流强度剖面及湍流积分尺度的分布。湍流强度与风洞试验结果进行对比如图5所示,从图5可看出数值风洞与风洞试验的湍流强度剖面趋势相同,但在数值上有差异。采用DSRFG方法生成的入口处的瞬时风速分布图,如图6所示。 图5 入口湍流强度及积分尺度剖面 图6 DSRFG方法产生的入口瞬时风速场 通过DSRFG方法生成的入口处脉动风速时程的功率谱与目标谱卡曼谱的比较如图7所示。由图7可知,大涡模拟所生成的脉动风速时程功率谱与目标谱一致,故其功率谱特性符合大气边界层湍流。其他边界条件,见表1。 表1 边界条件设置 图7 DSRFG方法生成的脉动风速时程功率谱与目标谱比较 在结构动力响应计算中,设置大楼在基础处的约束为3向固定约束(Fixed Support)。在workbench有限元模型中,设置建筑物除去底面的其他面为流固耦合面(Fluid Solid Interface)。 对未考虑流固耦合的刚性模型与考虑流固耦合的模型流体部分均采用分离涡模型作为湍流模型。分离涡模型是Spalart于1997年提出的一种三维非稳态数值模型,其原理是在模型近壁面采用RANS模型进行模拟,而在远端采用LES方法模拟,在保证相对高的计算精度的同时,有效降低了计算量。为获得较高的分离涡模拟精度,本文选用延迟分离涡模拟[10-11](Delayed Detached Eddy Simulation,DDES)进行分离涡的计算。该方法构造了一个转换函数fd,表达式为: fd=1-tanh[(8rd)3] (3) 其中, (4) 式中:νt为运动学涡黏性;ν为分子黏度;Uij为速度梯度;k为卡门常数;d为距壁面距离。 利用fd对经典分离涡模型进行修正,能够重新定义分离涡模型的长度尺度,延迟了RANS模型的作用范围,有效解决由于边界层网格加密产生的模型应力损耗问题和网格诱导分离问题,提高模拟的准确度。为使分离涡模型的方程封闭,需要设定亚格子模型和RANS模型。分离涡模型选择湍动能运输亚格子模型(Kinetic-Engergy Transport,KET),由Kim等[12]提出,这种亚格子模型对不均匀湍流的复杂流场有着较好的模拟效果。RANS模型则设定为Realizablek-ε两方程模型。对于考虑双向流固耦合的模型,采用分离涡模型进行流场的数值模拟,亚格子模型设置与刚性模型相同。 对流体的求解基于流体计算软件Fluent,采用分离涡法对台北101大厦进行模拟计算。对风场的计算采用3D单精度、分离式求解器,空气模型选用不可压缩的常密度空气模型,基于压力求解器(Pressure-Based),时间类型选择瞬态(Transient),求解算法采用SIMPLEC算法,离散格式选用二阶迎风格式。时间步长设置为0.05 s,时间步数设置为12 000。为获得较稳定的入口湍流,将定常Standardk-ε模型计算结果通过瞬态化处理作为分离涡模型计算的初始场。 在workbench有限元模型中,不仅要设置流体的求解参数,还要对耦合求解模块进行设置。在Workbench平台耦合计算模块中设置求解类型为瞬态(Transient),迭代结束时间设置为600 s,时间步长为0.3 s,每步最大迭代子步采用默认的5步,将流体部分的建筑物表面与固体部分的流固耦合面进行数据传输,并设置计算顺序,即流体计算-固体计算依次迭代,最终计算完成后在分析模块中查看计算结果。 本文对考虑流固耦合与未考虑流固耦合的数值模拟模型进行流场分析,分离涡模型在考虑流固耦合与未考虑流固耦合情况下风场中平均流速分布及模型y=0平面涡量分布见图8、9。 由图8~9可以看出,对于考虑流固耦合的气弹模型与未考虑流固耦合的刚性模型,来流在建筑周围表现出相似的典型钝体扰流的流场特点。上部来流越过建筑物顶端后向下分离,在建筑顶端背风处形成驻涡区。来流通过建筑物顶端与两侧绕流,不同频率的风速脉动与分离区域中的涡旋结构相互作用,在建筑侧面与背风面形成密集的涡旋脱落,这也是高层建筑横风向脉动风力产生的主要原因。 (a)刚性模型y=0平面 由图9(a)、(c)可以看出,相比于有限元模型,刚性模型周围涡量分布更为密集,尾流区域也更广泛,这使得不考虑流固耦合的模型顺风向加速度与位移响应均大于考虑流固耦合的模型。由图9(b)、(d)可以看出,双流固耦合作用下建筑背面尾流区域较刚性模型存在明显的旋涡脱落现象,旋涡更多且涡量更大。但在有限元模型中,建筑侧面的分离泡在形成初期即与建筑分离,形成脱落涡旋时也与建筑距离较远,而对于刚性模型,两侧的分离泡与建筑有较大的附着面积,建筑物两侧涡量明显大于气弹模型,这使得刚性模型中建筑受到更大的横向力影响,在风致响应中则表现为未考虑流固耦合的模型拥有更大的横风向位移与加速度。在有限元模型中,漩涡脱落时其涡量较大,可能会对其下游的毗邻建筑造成影响。 (a)刚性模型y=0 对台北101大厦ANSYS有限元模型与workbench有限元模型进行模态分析,将前五阶自振频率与实测数据进行对比,将结果列于表2。从表2可看出,ANSYS模型模态计算值与实测值差距都在15%以内,而workbench模型模态计算值与实测差距在5%以内,具有较高的精确度与可信度。 表2 前五阶振型自振频率计算值与实测值对比 本文采用规范计算以及时域分析两种方法,对台北101大厦等效静力风荷载进行计算。 规范中顺风向风荷载标准值ωk按下式计算: ωk=βzμsμzω0 (5) 式中:βz为高度z处的风振系数;μz为风压高度变化系数,根据建筑结构荷载规范GB—50009—2012[13]中B类风场要求分层取值;μs为风荷载体形系数,对该建筑以高度超过45 m,长宽比为1的矩形截面高层建筑取值,取1.4;ω0为基本风压(kN/m2),台北地区50年重现期下基本风压取值0.7 kN/m2。横风向风荷载标准值按下式计算: (6) 时域分析法是对结构的动力响应时程,采用惯性风荷载方法计算建筑等效静力风荷载(ESWLS),在未考虑流固耦合的数值风洞中,在刚性模型计算中的每个时间步对大厦的表面风压进行积分得到大厦每层的风荷载时程数据,并将其施加在台北101大厦三维有限元模型上,在时域内用逐步积分法求解微分方程,得到结构的动力响应时程,在考虑流固耦合的情况下,结构的动力响应时程数据可直接由气弹模型计算得出。等效静力风荷载可表示为: (7) 两种计算方法与风洞试验数据对比见表3。从数据对比结果可以看出,顺风向上考虑双向流固耦合与未考虑流固耦合的建筑等效静力风荷载较为一致,二者与风洞试验结果相差不大;横风向和扭转方向上,未考虑流固耦合的等效风荷载略小于高频天平测力风洞试验结果。这是因为数值模拟中未对建筑周边建筑进行考虑,风洞试验中考虑了主体建筑600 m半径范围内所有主要建筑物,且风洞试验中风场的湍流特性也与数值模拟存在一定差别;值得注意的得是考虑双向流固耦合后,横风向等效静力风荷载则大大减小。此外,数值模拟计算结果与规范计算结果有一些差别,这是因为规范是对结构进行简化计算,且只考虑结构一阶响应,对建筑层间结构引起的风场湍流特性与高阶振型影响无法充分考虑。 表3 各工况等效静力风荷载(结构阻尼比=2%) 计算与现场实测得到的大楼最高居住层第89层处,X及Y轴方向上的加速度功率谱对比如图10所示。从图10中可看出,计算的加速度功率谱与实测谱吻合较好。 (a)x方向加速度功率谱 通过有限元瞬态动力分析得到台北101大厦最高居住层(第89层)在50年重现期[14]风速条件下的位移时程与加速度时程曲线,50年重现期风速条件下建筑物最高居住层加速度与位移时程曲线,如图11所示。 (a)顺风向加速度 从图11可以看出,计算稳定后大厦最高居住层的横风向加速度响应占据主导地位。考虑流固耦合作用时顺风向最大加速度为0.11 m/s2,最大位移为0.56 m,横风向最大加速度为0.15 m/s2,最大位移为0.32 m;而未考虑流固耦合时顺风向最大加速度为0.18 m/s2,最大位移为0.59 m,横风向最大加速度为0.86 m/s2,最大位移为0.67 m。在顺风向上,ANSYS有限元模型的加速度与位移响应均略大于workbench有限元模型,这是由于有限元模型背风面分布密集的分离涡对建筑产生了负风压。在横风向上,ANSYS有限元模型在加速度和位移响应均远大于workbench有限元模型,这是由于有限元模型中紧密附着在建筑两侧的分离涡对建筑造成的巨大横向力。对比两组模型的加速度时程数据可以看出,总体上看,ANSYS有限元模型最大位移、最大加速度比workbench有限元模型结果大30%以上。由计算可知,台北101大厦最高居住层居民在50年重现期风速条件下会感到不适,但在可接受范围之内,满足在工程实践中的要求。 本文以台北101大厦为研究对象,基于结构动力学特性相似原理,利用 Workbench平台建立大厦的有限元模型并进行流固耦合数值模拟,并将计算结果与现场实测以及风洞试验的相应数据进行了对比,以验证数值风洞的有效性。监测振动稳定后400 s内建筑物最高居住层的位移与加速度时程等风致响应,并将其与未考虑流固耦合的ANSYS三维有限元模型进行对比,主要结论如下: (1)由刚性模型的数值风洞与实体风洞测得等效风荷载对比可知,采用DSRFG湍流生成方法的DDES模型具有较高的准确性与可信度。在非定风场的模型中,DDES模型能够较好的预测出建筑物侧面与背后的旋涡分布现象,对复杂风场有足够强的预测能力。 (2)台北101大厦超高层建筑振动以横风向为主。在考虑流固耦合效应后,建筑顺风向位移及加速度响应变化较小,而建筑物最高居住层(89层)横风向位移响应与加速度响应均明显减小,这表明考虑流固耦合效应在对该栋建筑进行数值风洞模拟时是必要的。 (3)考虑流固耦合情况下,建筑模型横风向等效风荷载显著降低,顺风向等效风荷载则保持不变。在双向流固耦合作用下,来流将在建筑背风处形成涡量较大的脱落旋涡,可能对下游毗邻建筑风稳定性造成影响。
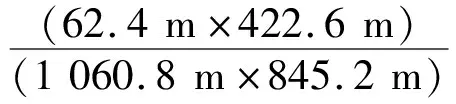

3.2 边界条件



3.3 湍流模型
3.4 求解参数
4 数值模拟结果分析
4.1 流场分析


4.2 模态分析

4.3 等效静力风荷载



4.4 位移和加速度响应

5 结 论
