一种改进的DQG格网编码与经纬度高效转换算法

丁加成，赵学胜

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

0 引言

球面退化四叉树格网(Degenerate Quadtree Grid,DQG)[1]是一种建立在经纬度格网基础上的变间隔经纬度格网模型，具有径向对称性、方向一致性及平移相和性等优点[2]，其四边形网格的投影为矩形[3]，适用于数字地形的构建和遥感影像的管理等[4,5]，是全球地表建模及可视化分析[6]的基础框架之一。格网利用编码表达空间对象，而现有空间数据多以经纬度的形式存在[7]。因此，编码与经纬度间的转换效率是制约格网应用的重要因素[8]。随着空间信息获取技术的进步和更新频率的加快，时空数据量急剧增加[8,9]，数据类型也日益丰富[10]，对格网编码与经纬度间的转换效率提出了更高要求。

国内外学者提出了诸多格网编码与经纬度转换方法。例如：ZOT (Zenithal Ortho Triangular)投影法[11]按曼哈顿距离进行转换，效率较高，但编码失去方向性，不便于邻近搜索；等三角投影法(Equal Triangles Projection,ETP)[12]计算精度较高，但涉及投影操作及幂指数运算，效率较低；行列逼近法[7]在保证算法效率的同时，生成的编码具有方向性，但存在半个格网误差；三向互化算法[13]有效降低了转换误码率，其转换速度介于行列逼近法和ZOT算法之间；王谦等[8]对行列逼近法和三向互化算法进行改进，提高了编码转换精度；张玉梅等[14]提出的球面菱形格网与经纬度转换算法不涉及投影操作，计算速度较快。上述算法在编码与经纬度间转换时存在递归过程，转换效率有待提升。针对DQG格网编码，崔马军等[15]最早利用DQG和经纬度格网的对应关系提出相应的转换算法，实现简单，但其采用四进制编码，转换效率需进一步提升；余接情等[16]对DQG进行三维扩展，提出一种球体退化八叉树立体格网SDOG，采用二进制方式存储编码，并设计对应的单层次和多层次格网编码方式，但需进行多次浮点运算，使用逐位处理进行编码/解码，特别是处理海量数据时，其效率仍需进一步提升。

为适应海量格网数据的实时计算与分析需求，本文在现有算法基础上进行改进：用二进制代替四进制编码，并推导出格元行号和经度差间关系，优化格元列号计算方式，以期提高编(解)码效率，为海量时空大数据的高效转换和实时分析提供可能。

1 DQG格网剖分与八分体编号

随着纬度升高，DQG格元的经度差自适应变大，在极点周围退化为三角形。为分析DQG格元的分布特征，构建DQG格元的行号、列号、格元经纬差以及剖分层次间关系，本文引出梯形区域的概念。

1.1 梯形区域的定义

余接情等[16]定义纬域为同一层域中经度差相同的格元集合。由于DQG中没有层域的概念，纬度的计算过程不涉及层域，本文定义八分体内经度差和纬度差均相同的格元集合为梯形区域。对同一剖分层次，格元纬度差相同，因此，梯形区域的定义可简化为八分体内经度差相同的格元集合，八分体由多个梯形区域组成。如图1所示，将梯形区域按纬度由高到低进行编号，最大编号kmax=剖分层次level，包含极点的退化三角形编号为0。图中右侧数字表示各梯形区域内格元的行数，除0号区域外，梯形区域内格元的列数是行数的两倍。

图1 梯形区域的分布和编号Fig.1 Distribution and serial number of trapezoid areas

1.2 梯形区域编号与行列号间关系

表1 梯形区域的行数和列数Table 1 Number of rows and columns of trapezoid areas

(1)

(2)

(3)

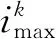
(4)

(5)

将式(3)和式(4)代入式(5)，当k=0时，0≤i≤0，即i=0。当k>0时有以下关系成立：

(6)

对不等式取对数可得：

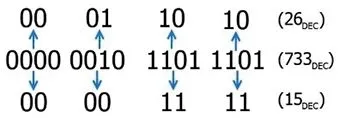
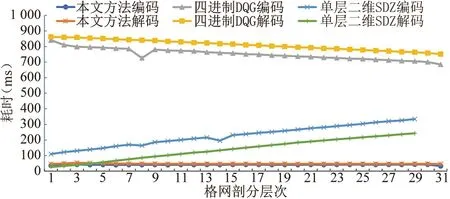
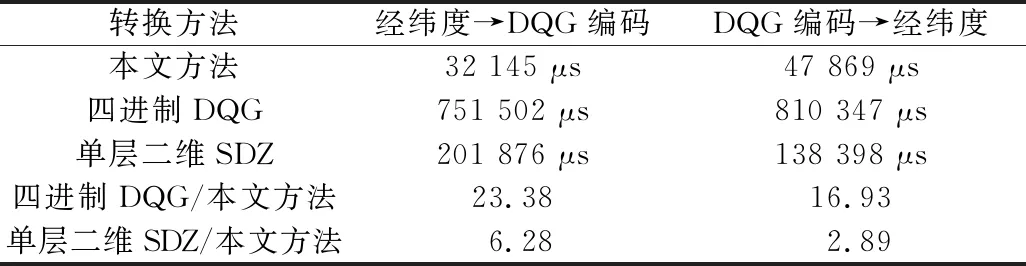
k-1

(7)

即：

(8)

由式(8)可知，格元所在的梯形区域编号由格元行号决定，与输入点纬度和剖分层次无关，反映了DQG格元的分布规律。将i=0代入式(8)，得k=0，即式(8)在i=0时仍然适用。

1.3 格元经纬差计算

八分体的经度范围为[0,π/2]，由行内格元平分，结合式(2)可计算i行格元经度差：

(9)

将式(8)带入，可得

ΔLi=π/2log2(i+1)+1

(10)

2 DQG编码及转化方法

2.1 编码存储方式

本文以自定义结构体存储格网编码，用C++语言描述(图2)。其中，整型成员m_morton存放格元行列号对应的二进制Morton码，无符号字符成员m_oct_level的高三位存放八分体编号，低五位存放剖分层次，每个编码占据9 B存储空间。编码能表达的最大剖分层次为32，对应格网单元最大边长小于4 mm[2]，能满足多数空间分析和表达的精度要求。

图2 格网编码结构体定义(C++描述)Fig.2 Grid code structure definition (C++)

2.2 Morton编码与解码

现有的DQG格网编码/解码方式多采用逐位处理实现[15-17]，效率不高。使用查找表进行编码和解码时，一次可处理多个二进制位，计算效率较高，故本文利用查找表[18]，结合位运算实现Morton码的编码和解码。二维情况下，可建立大小为2m的查找表(m为映射位数)。当m较小时，需进行映射的次数较多，效率较低；当m较大时，需建立的查找表较大，占用存储空间较大。综合考虑，本文取m=8。

编码过程是将各维编号的二进制位按m位为一组分为若干组，每组利用查找表进行编码映射，并将结果进行拼接，然后将各维编号经过映射和拼接后的二进制位进行移位，并进行按位或运算；解码过程是对Morton码的二进制位按m位为一组分为若干组，从每组二进制位中分解出各维的二进制位并进行拼接，即得到各维的二进制表示。图3和图4展示了映射位数m=4，对行号i=26和列号j=15进行编码和解码的过程。

图3 查找表编码过程Fig.3 Morton encoding using look up table

图4 查找表解码过程Fig.4 Morton decoding using look up table

此外，还可以使用位操作指令集(BMI2)中的并行位存储指令pdep和并行位提取指令pext实现Morton编码和解码。经测试，其计算效率和查找表法基本相同。

2.3 经纬度坐标与DQG编码间转换算法

在DQG格元编码和解码过程中，需要计算格元纬度差、八分体编号及进行八分体内经纬度和全球经纬度间转换，计算过程见文献[15,16]。

2.3.1 经纬度坐标向DQG编码转换算法 输入数据为经纬度坐标(L,B)、剖分层次level，输出数据为经纬度对应的DQG格元编码。1)由经纬度计算其所在八分体编号oct；2)由oct计算八分体内经纬度(L′,B′)；3)利用剖分层次level计算格元纬度差ΔB；4)由ΔB按式(11)计算格元行号i；5)按式(10)计算i行格元经度差ΔL；6)按式(12)计算格元列号j；7)将i和j的二进制交错成Morton编码，存放在DQG格网编码成员m_morton中，设置成员m_oct_level的高三位为八分体编号，低五位为剖分层次。

(11)

(12)

2.3.2 DQG编码向经纬度坐标转换算法 输入数据为DQG格元编码，输出数据为编码对应格元的中心点经纬度。1)提取编码成员m_oct_level的高三位为八分体编号oct，低五位为剖分层次level；2)对编码成员m_morton进行解码，得到行号i和列号j；3)计算格元纬度差ΔB，并按式(13)计算格元中心点的八分体内纬度Bc；4)由式(10)计算i行格元经度差ΔL，并按式(14)计算格元中心点的八分体内经度Lc；5)由oct和编码格元中心点的八分体内经纬度(Lc,Bc)，计算对应的全球经纬度。

Bc=π/2-(i+0.5)ΔB

(13)

Lc=(j+0.5)ΔL

(14)

3 实验分析与效率对比

实验运行环境为虚拟机，硬件配置为RAM 3 GB，CPU AMD R5 4600H，核心数4，磁盘空间40 GB，操作系统为Ubuntu 20.04 LTS，编译器版本GCC 9.3.0。实验随机生成分布于全球的100万个经纬度坐标，分别测试本文方法与四进制DQG[15]、单层二维SDZ[16]编码和解码的效率(图5)，并计算不同剖分层次下各转换算法的平均转换时间(表2)。

图5 编码转换速度对比Fig.5 Comparison of code conversion speed

表2 编码转换算法耗时Table 2 Time consumption of code conversion algorithm

由表2可以看出，四进制DQG[15]编码和解码耗时分别是本文方法的23.38倍和16.93倍，而单层二维SDZ[16]编码和解码耗时分别是本文方法的6.28倍和2.89倍。若开启编译器最高优化级别编译程序，使用本文方法对100万个随机生成的地理坐标进行编码耗时17 618 μs，将编码转换为地理坐标耗时10 358 μs。在虚拟机的配置环境下，每秒可实现约5 676万个经纬度坐标的编码及约7 364万个编码的解码，基本能满足海量地理坐标与格网编码间的高效转换。

4 结论

格网编码与经纬度间转换效率是影响海量空间数据集成和分析的重要因素。本文通过分析DQG格网剖分的特征，推导出格元经度差和行号间的数学关系；使用查找表法进行二进制DQG编码与经纬度的转换，提高了计算效率。与现有转换算法不同，本文算法可根据格元所在行号直接计算格元经度差。实验表明：本文算法的编码和解码的平均速度是四进制DQG算法的20.15倍，是单层二维SDZ算法的4.58倍；单机情况下可进行每秒千万级的格网编码与解码，为海量格网数据的实时分析奠定基础。但本文方法也存在一定不足，如编码存储的格元剖分层次有一定限制，转换过程中的浮点数运算会降低计算效率等。下一步研究考虑使用字节数组存储编码以提高编码的最大剖分层次，并使用异构计算进一步提高格元编码与经纬度的转换效率。