顾及风向和风速的气温空间插值方法

曹端广，张子民*，王 海，常鲁群

(1.山东建筑大学测绘地理信息学院，山东 济南 250101；2.济南市勘察测绘研究院，山东 济南 250101)

0 引言

气温不仅是自然地域系统界限划分的关键指标，还是陆地环境过程模拟的重要参数[1,2]，广泛应用于生态环境评价、自然灾害检测、农业生产和气候变化等领域[3-6]，故对气温进行空间化对于研究全球气候变暖对生态系统的影响至关重要[7，8]。已有研究常基于气象站点实测气温数据利用空间插值方法(反距离加权法、克里金法、自然邻近法、样条函数法、趋势面法等[9])预测未知点数据[10]，例如：Stahl等比较了12种基于回归和加权平均的气温插值方法，发现选择控制站点与计算权重的方法比计算高程的方法对预测精度的影响更小[11]；Hutchinson等在样条函数插值法的基础上考虑了海拔对气候要素的影响，提出了薄盘光滑样条插值方法(Thin Plate Smoothing Spline，TPS)，并开发了相应的插值软件ANUSPLIN[12]；Nalder等通过结合多元线性回归法和地理加权回归法提出了梯度下降反比法(GIDW)，提高了插值结果的精度[13]；徐翔等通过比较普通克里金法、反距离加权法以及将高程作为协变量的薄盘光滑样条插值法，发现薄盘光滑样条插值法适于复杂山地环境下气候要素的空间插值[14]；刘正佳等研究得出，薄盘光滑样条插值法适用于全国大部分地区在区域尺度上以DEM为协变量的插值[15]。

综上可知，当前气温空间插值方法多将高程、经纬度等作为影响因素，未考虑气象数据中风向和风速对气温空间插值的影响。我国冬季盛行的西北风起源于西伯利亚高压，其将西北冷空气吹向东南方，使我国大部分地区气温降低，而夏季则相反[16]。陆福志等通过建立秦岭—大巴山气温与降水格点数据集，发现秦岭阻挡冬季季风南下，从而影响冬季气温空间分布[9]，可见季风对气温影响很大。与高程数据不同，风向和风速数据既有大小也有方向，因此，不能将风向和风速数据直接作为薄盘光滑样条插值的协变量，需对其进行量化。谢瑶瑶等对中国1951-2008年的气温站点数据进行了严格的统计学分析，证明气温服从正态分布，符合高斯扩散模型的假设条件[17]；Li等利用风向数据与最短路径算法提出风场最短路径，并将其代替反距离加权插值(IDW)中的欧氏距离进行空气污染物空间插值[18]。

本研究在已有气温与污染物插值研究的基础上，提出一种顾及风向和风速的气温空间插值方法，并分别以累计移动成本最短路径(SPOCMC)、高程(DEM)和SPOCMC-DEM作为协变量进行薄盘光滑样条插值，通过分析不同方法插值结果的误差验证本文方法的准确性。

1 研究方法

本文研究方法具体实现步骤(图1)为：1)根据气象站点观测的风向、风速数据进行插值，生成连续的风场表面；2)基于该风场数据利用高斯扩散模型构建扩散成本表面；3)利用Dijkstra最短路径算法计算观测点与待求点的累计移动成本最短路径(SPOCMC)；4)将SPOCMC作为协变量进行薄盘光滑样条插值以实现气温插值。

图1 本文方法流程Fig.1 Flowchart of the proposed method in this paper

1.1 双线性内插生成风场表面

由于风场是矢量数据，对风向和风速进行插值生成连续的风场表面，需将矢量风分解为东西、南北两个方向的笛卡尔分量，然后采用双线性插值法，即在两个方向分别进行一次线性插值[19]。如图2所示，假设已知函数f在Q11=(x1,y1)、Q12=(x1,y2)、Q21=(x2,y1)、Q22=(x2,y2)4个点处的值，为求得未知函数f在点P=(x,y)处的值，首先在x方向进行线性插值，得到式(1)、式(2)，然后在y方向进行线性插值，得到式(3),即可得到f(x,y)(式(4))。

图2 双线性插值示意Fig.2 Schematic diagram of bilinear interpolation

(1)

(2)

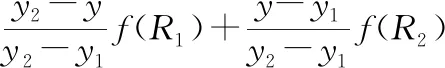
(3)

(4)

1.2 基于高斯扩散模型构建成本表面

为计算累计移动成本最短路径，需要求出待求点到已知点的移动成本。本文利用高斯扩散模型(式(5))模拟气温在风场作用下的移动距离，以此作为两点之间的移动成本，并假设气温受风力作用在水平和垂直方向符合正态分布，风力为均匀连续的作用力[18]。

(5)

式中：C0(x,y,z,u)表示气温；x和y分别表示下风向距离和待求点与风向中心线的水平距离；z表示污染物在扩散中的释放高度，本研究将z设为固定值；u表示水平风速；σy和σz分别表示水平和垂直方向的扩散标准差。

由于高斯扩散模型用于模拟污染物从特定来源的扩散，而热量不能点源化，且不像污染物有稳定的扩散源，故该模型不能直接应用于本研究，但能说明热量在风场作用下移动成本的起源。将高斯扩散模型中的笛卡尔坐标(x,y)转换为极坐标后，可以看出浓度会随距离γ和方位角θ的增大而减小，所以将高斯扩散模型化简[18]可得：

CostAB=[F(DA,DM)+F(DB,DM)]×LAB

(6)

F(DA,DM)=[|cos(|DA-DM|)|×VA]-sgn[cos(|DA-DM|)]

(7)

F(DB,DM)=[|cos(|DB-DM|)|×VB]-sgn[cos(|DB-DM|)]

(8)

式中：VA和VB分别代表A、B网格单元的风速；cos(|DA-DM|)为A网格单元的风速在AB方向上的分量，其值的正负分别代表对下风向和上风向的作用：作用于下风向时，风速越大，站点温度对下风向温度贡献越大，反之则贡献越小；而作用于上风向时，风速越大，站点温度对上风向温度贡献越小，反之则贡献越大。

1.3 计算累计移动成本最短路径(SPOCMC)

在移动成本表面的基础上，采用最短路径Dijkstra算法[20]计算待求点到已知点的累计移动成本最短路径(SPOCMC)。算法的输入条件包括起点与终点在格网中的位置和所有格网单元的有向加权邻接矩阵(其权值为式(5)计算出的移动成本)，算法的输出结果为累计移动成本最短路径，包含最短路径和最短路径长度。计算过程如图3所示，将风场表面划分为规则格网，网格线上的数值代表相邻网格点之间的移动成本，通过式(5)将风向和风速的矢量数据分解到网格的每条边上进行相邻网格间移动成本的求解，图中加粗路径为累计移动成本的最短路径，其方向与分解到规则格网后的风向一致。

图3 累计移动成本最短路径计算Fig.3 Calculation of the shortest path of cumulative moving costs

1.4 薄盘光滑样条插值法的气温插值

薄盘光滑样条插值法实现了模型的平滑度和精确度的最佳融合，极大提高了插值精度。将累计移动成本最短路径(SPOCMC)作为协变量进行薄盘光滑样条插值，以实现顾及风向和风速的气温空间插值。薄盘光滑样条的理论统计模型为：

zi=f(xi)+bTyi+ei

(9)

式中：zi为位于空间i(i=1,…,N)点的因变量；xi为d维样条独立变量矢量；f为要估算的关于xi的未知光滑函数；yi为p维独立协变量矢量；b为yi的p维向量系数；ei为期望值为0、方差为ωiσ2(ωi为作为权重的已知局部相对变异函数，σ2为误差方差，在各数据点上均为常数，且一般未知)的自变量随机误差。

函数f与系数b通过最小二乘法进行估计：

(10)

式中：Jm(f)为函数f(xi)的m阶偏导数，称为粗糙测次数或样条次数；ρ为正的光滑参数，用于平衡曲面的粗糙度和数据的保真性。

2 方法验证

2.1 研究区与数据

考虑到气象观测点分布以及地形的影响，选择风向和风速较为稳定、地势较为平坦的山东省作为试验区域。山东省位于中国东部沿海、黄河下游，省内中部山地突起，西南、西北低洼平坦，东部缓丘起伏，形成以山地丘陵为骨架、平原盆地交错分布的地形大势。实验数据(图4)包括：1)气象站点数据，从中国气象数据网(http://data.cma.cn/)获取山东省109个气象站点逐小时观测温度、风向和风速数据；2)DEM数据，从地理空间数据云(http://www.gscloud.cn/)上下载山东省90 m空间分辨率的SRTM DEM UTM 数据。

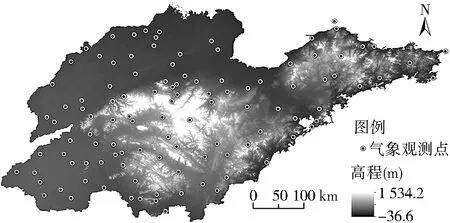
图4 山东省气象站点分布Fig.4 Distribution of meteorological stations in Shandong Province

2.2 不同协变量的薄盘光滑样条插值

为验证本文方法可有效提高气温空间插值的准确性，分别以累计移动成本最短路径(SPOCMC)、高程(DEM)和SPOCMC-DEM作为协变量进行薄盘光滑样条插值，对比不同插值方法的精度。选取山东省109个观测站点2019年每月15日9：00的气温、风向和风速数据作为实验数据，采用上述3种方法进行气温空间插值，图5为7月15日9：00的气温空间插值效果图。

从图5a可以看出，以高程(DEM)为协变量进行薄盘光滑样条插值时，研究区中西部出现气温低值点，缘于泰山位于该处，高程较大，气温偏低；本文SPOCMC法顾及了风向和风速影响，插值结果(图5b)显示，受东南风影响，泰山低温区域较图5a向西北方向有所偏移，东部沿海低温区域也向内陆扩散；从SPOCMC-DEM法的插值效果图更能明显看出受风力影响的气温扩散趋势，在泰山低温点处呈现出近似条带状的扩散路径。

图5 空间插值效果Fig.5 Spatial interpolation effect

2.3 误差分析方法

采用交叉验证方法[21,22]对109个观测站点12个月的数据进行插值，运用表征估计值误差范围的平均绝对误差(MAE，式(11))、反映数据估值灵敏度和极值效应的均方根误差(RMSE，式(12))评估SPOCMC法、DEM法和SPOCMC-DEM法的气温插值精度并进行对比分析(表1)。

(11)

(12)

由表1可知，SPOCMC-DEM法的MAE和RMSE均值分别为0.517、0.779，比SPOCMC法(0.583、1.016)分别降低了11.32%、23.32%，比DEM法(0.809、1.231)分别降低了36.09%、36.72%，表明本文累计移动成本最短路径(SPOCMC)法的气温插值精度要高于DEM法，当同时使用SPOCMC和DEM作为协变量进行薄盘光滑样条插值时效果更优。

表1 3种插值方法误差统计Table 1 Error statistics of three interpolation methods ℃

由图6可直观地看出3种插值方法的精度对比结果，总体上SPOCMC-DEM法的MAE和RMSE最小，其次为SPOCMC法，DEM法最大。3种方法的MAE、RMSE在6-8月略有增大，原因是研究区夏季气温空间差异明显，导致插值结果误差增大;春、秋季气温空间差异较小，致使3-4月、9-11月的MAE、RMSE值降低，插值结果精度提升。

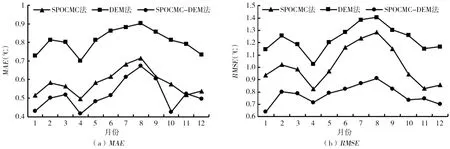
图6 误差分析折线Fig.6 Broken lines of error analysis

2.4 方法适用性分析

为验证本文方法在不同地区的适用性，选取江苏省和贵州省两个具有地形代表性的省份进行实验，其中江苏位于我国东部沿海地区，地貌主要为平原，贵州地处我国西南内陆腹地，地貌类型复杂，包括山地、丘陵、高原和盆地。分别选取两省份2019年3月、6月、9月和12月15日9：00的气温观测数据，采用3种方法进行气温插值并统计误差(表2)。

表2 3种插值方法在两个研究区域的误差统计Table 2 Error statistics of three interpolation methods in two study areas ℃

从表2可以看出：江苏的实验结果中，SPOCMC法的MAE和RMSE值明显小于DEM法,这是由于江苏地处平原，区内高程差异较小，所以高程对气温插值造成的影响较小；贵州的实验结果中，SPOCMC法的MAE和RMSE值比DEM法大，原因是贵州的地形多为丘陵和山地，高程对气温插值影响较大；而使用SPOCMC-DEM法在两省进行插值的MAE和RMSE值均小于SPOCMC法和DEM法，充分证明了添加SPOCMC协变量可提高气温插值的精度。

2.5 算法复杂度分析

算法的计算耗时与样本数量直接相关，本文分别采用SPOCMC法、DEM法和SPOCMC-DEM法对江苏、贵州和山东3省的数据进行气温插值，同时计算3种方法在不同样本数量情况下的执行时间(表3)。可以看出，3种方法的计算耗时随样本数量的增加而增大，SPOCMC法对于不同样本数量的计算时间均明显大于DEM法，SPOCMC-DEM法的计算耗时最多。

表3 3种插值方法的性能统计Table 3 Performance statistics of three interpolation methods s

设n为样本数量，m为待插值点的数量。传统的以DEM为协变量进行薄盘光滑样条插值需要迭代m次，时间复杂度为Ο(mn)，空间复杂度为Ο(n2)。本文算法在传统方法的基础上需要额外计算累计移动成本最短路径，第一步采用双线性内插法生成风场表面需要进行两次循环次数为n的循环，时间复杂度为Ο(n2)，空间复杂度为Ο(1)；第二步利用高斯扩散模型的改进公式计算移动成本的时间复杂度为Ο(n)，空间复杂度为Ο(1)；最后采用最短路径Dijkstra算法计算待求点到已知点的累计移动成本最短路径，其对应的时间复杂度为Ο(n2)，空间复杂度为Ο(E)(E代表路径数)。综上，本文算法的总时间复杂度为T(m,n)=Ο(mn)+Ο(n2)+Ο(n)+Ο(n2)=Ο(max{mn,n,n2})，空间复杂度为S(n,E)=Ο(n2)+Ο(1)+Ο(1)+Ο(E)=Ο(max{n2,E})，与传统方法相比，时间复杂度和空间复杂度均有所增加。由于实际气温插值工作中样本点数量有限，且算法增加的时空复杂度对于实际工作并不会产生较大影响，所以本文算法仍具有较高的实用性和有效性。

3 结论

本文提出一种顾及风向和风速的气温空间插值方法，并以SPOCMC、DEM和SPOCMC-DEM分别作为协变量对山东省109个站点12个月份的气温数据进行薄盘光滑样条插值比较，结果表明：以SPOCMC-DEM作为协变量进行插值的MAE、RMSE均值分别为0.517、0.779，略小于以SPOCMC作为协变量插值结果的均值(0.583、1.016)，明显小于以DEM作为协变量插值结果的均值(0.809、1.231)，说明该方法相比通常以DEM为协变量的薄盘光滑样条气温插值方法精度明显提高，当同时以SPOCMC和DEM为协变量进行插值时，效果更优。江苏省和贵州省的插值实验结果证明了该方法具有普适性。由于本研究的风场模型仅考虑了风在水平方向上的作用力，若将垂直方向上的作用力也纳入模型中，可能会进一步提高插值的精度。目前该算法计算量较大，有待进一步优化，以降低算法的时空复杂度。