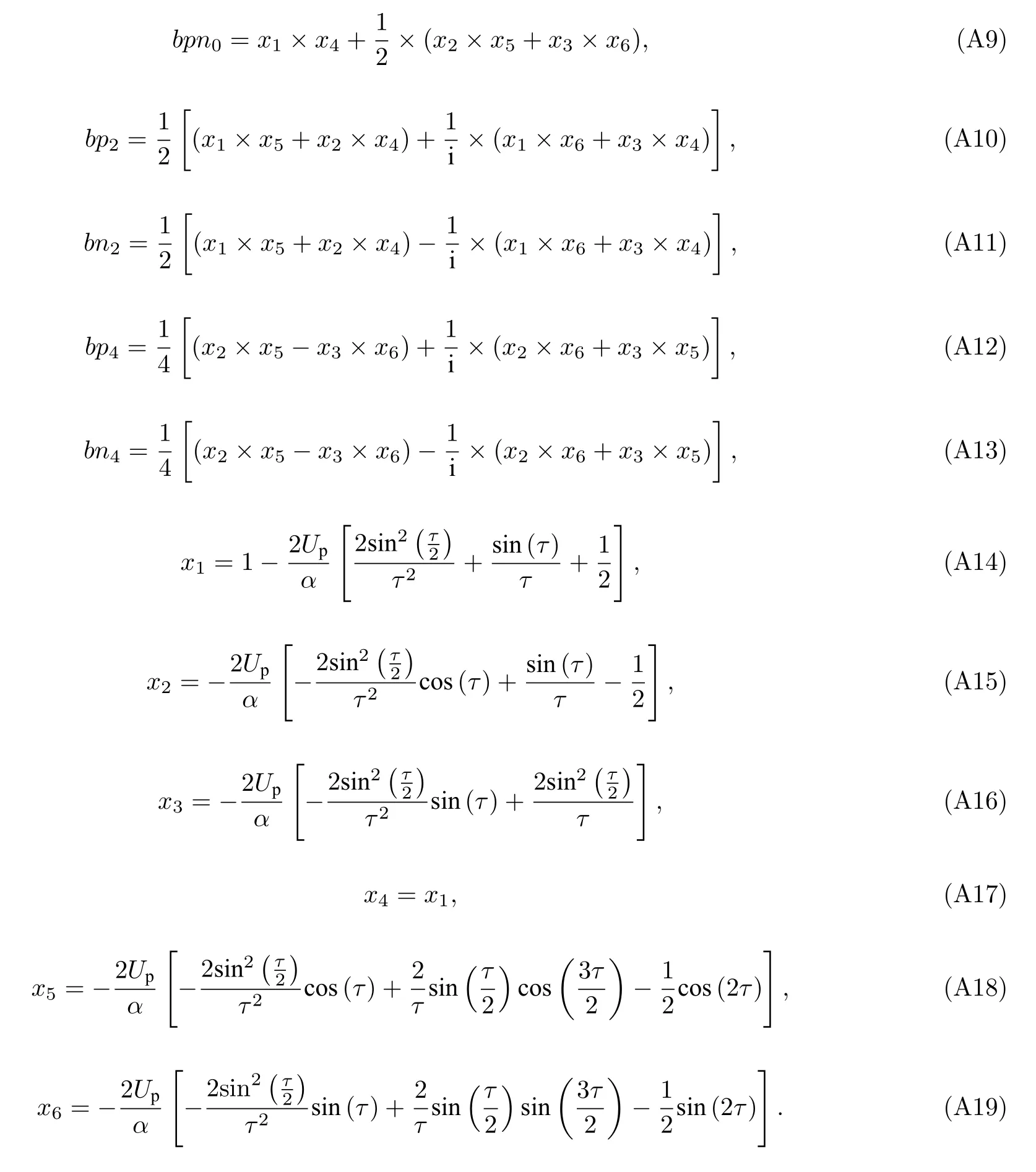原子基态函数对高次谐波谱影响的研究

李忠元,郭迎春,王兵兵

（1. 华东师范大学 物理与电子科学学院，上海 200241; 2. 中国科学院 物理研究所北京凝聚态物理国家重点实验室 光物理实验室，北京 100190）

0 引 言

处于强激光场中的原子、分子会产生频率为入射激光场频率整数倍的高次谐波. 人们发现谐波谱具有以下特点: 最初的谐波强度随谐波阶次的增加而迅速下降, 接着出现随阶次增加强度不变的平台区域, 最后在某一阶次处(截止频率)急剧下降为0. 高次谐波的这一特点使其成为潜在的超短脉冲光源及高频深紫外光源[1-3], 也使其逐渐成为测量分子准直[4-5]、分子[6-7]和原子[8]轨道, 以及凝聚态物质拓扑性质[9-10]的有力工具. 以上这一切都要求深刻理解原子及分子的结构与高次谐波的关系. 对于高次谐波的理解, Corkum[11]给出了著名的三步模型的物理图像: 电子先隧穿电离为速度为零的自由电子,在电场作用下运动; 电子获得动能, 并在激光场的驱动下回到母核附近, 发生复合; 辐射的高次谐波的能量为电子的动能与电离势能的和. Lewenstein等[12]在强场近似下解析求解薛定谔方程, 获得了谐波强度的积分表达式, 该强场近似理论对分析物理图像非常方便.

惰性气体一直都是高次谐波研究的首选对象[13-22]. 因为惰性气体原子中的电子是满壳层的, 电子的分布是中心对称分布的, 所以文献[18]用s轨道函数作为基态函数, 运用频域理论得到了惰性气体高次谐波谱和正确的截止频率. 文献[19]采用类氢的s轨道函数作为基函数, 探讨了双色场下氖(Ne)的圆偏振的高次谐波谱. 而在实际中, 参与高次谐波的电子在Ne、 氩(Ar)、 氪(Kr)、 氙(Xe)原子气体中, 都是p电子. 文献[20]研究了惰性气体p轨道的空间分布大小对双色场下的高次谐波谱的影响, 强调了使用p轨道波函数的重要性. 文献[21]探讨了p电子轨道对双色场下的Ne的圆偏振的高次谐波谱的影响. 文献[22]测量了氦气、氖气和氩气的HHG谱, 将它们的光谱的不同归因于复合步骤中原子轨道的影响. 本文采用Lewenstein理论[12], 在单电子近似下, 分别用高斯型的p电子和s电子的轨道波函数为基函数, 通过计算惰性气体的高次谐波谱, 探讨了基态函数的不同空间分布对高次谐波的影响; 通过p轨道情况和s轨道情况的比较, 获得了p轨道情况下高次谐波的独特特征.

本文的安排: 第1章原理部分, 首先概述Lewenstein等计算高次谐波的理论, 然后给出以s电子轨道函数为基态函数和以p电子轨道函数为基态函数这两种情况下计算高次谐波的表达式; 第2章,首先给出两种情况下谐波谱的计算结果并进行比较, 然后通过理论推导, 给出p轨道情况下谐波谱中出现凹陷结构的位置; 第3章给出结论.

1 Lewentein理论

原子在x方向偏振的激光电场Ecos(t)作用下, 其单电子近似的薛定谔方程为[12](本节的公式中涉及的能量都是以激光场频率ω为单位的, 即ω=1).

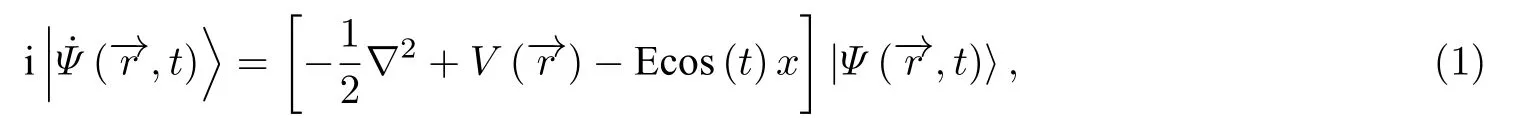
不考虑激发态对高次谐波的贡献, 并且忽略激光电场对原子态的影响, 得到电场方向的偶极矩

其中,

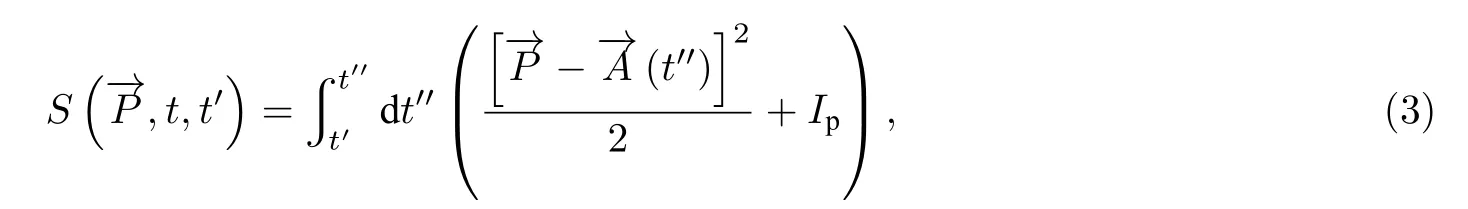
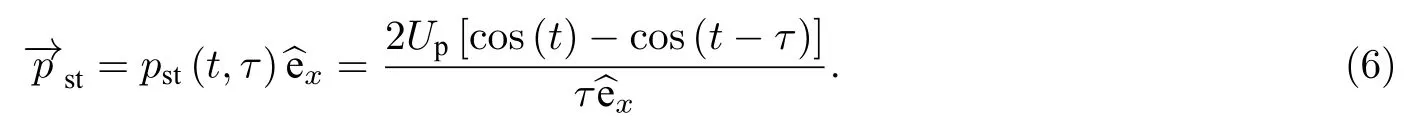
对偶极矩进行傅里叶展开, 获得高次谐波谱

2k+1阶高次谐波的强度为

1.1 高斯型s轨道函数为基态函数情况下的高次谐波

研究氢原子或惰性气体原子, 通常用高斯型s轨道函数来近似基态函数, 即

进而,

结合式(5)、式(6)、式(7)和式(10), 得到偶极矩的2k+1阶的傅里叶分量为

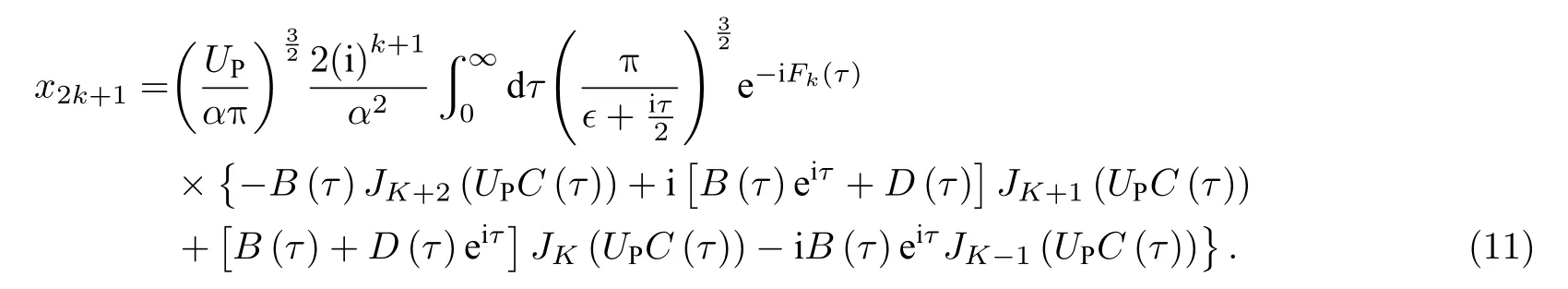
式(11)中的B(τ),D(τ),C(τ),Fk(τ) 的表达式见文献[12]附录中的A5–A8.

1.2 高斯型p轨道函数为基态函数情况下的高次谐波

对于氦(He)原子, 用上面的s轨道函数来近似基态函数是合理的, 因为参与高次谐波过程的是s轨道电子. 但对于氖原子、氩原子、氪原子、氙原子, 因为参与高次谐波过程的是p电子, 所以用p电子轨道函数作为基态函数更为合理. 在粒子坐标系中, p电子的波函数可近似为

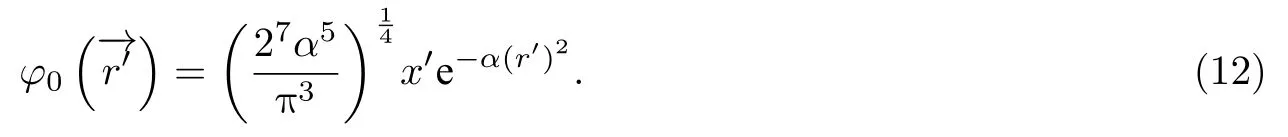
在实验室坐标系中, 因固定在粒子上的x′轴的方向角是 (θ0,φ0), 故而基态的波函数为

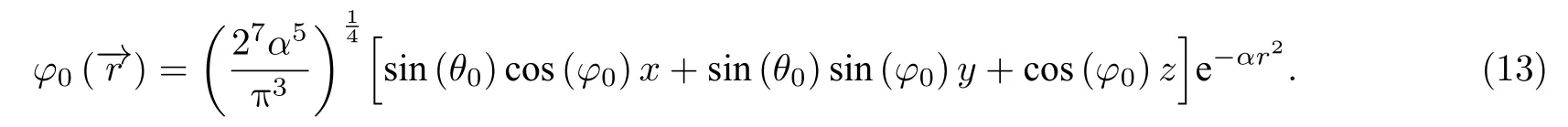
相应地

将鞍点式(6)以及式(14)代入式(5), 得到偶极矩, 经过繁琐的运算得到偶极矩的2k+1次的傅里叶分量为

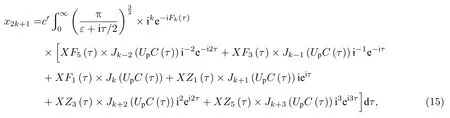
其中,

式(15)中的Fk(τ),C(τ),XF5(τ),XF3(τ),XF1(τ),XZ1(τ),XZ3(τ),XZ5(τ) 的表达式见文后附录A.

需要强调的是, 固定在原子上的粒子坐标系在固定的实验室坐标系中不是固定不变的, 即上面公式中的方位角 (θ0,φ0) 的取值是随机的, 所以最终的谐波的强度需要对方向角进行积分, 即

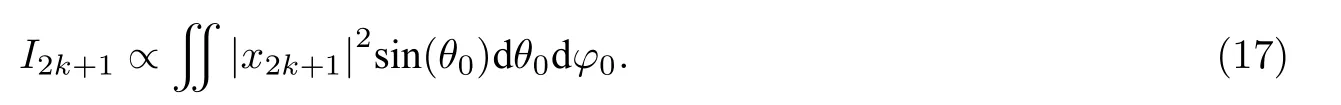
幸运的是, 在式(15)除c′外, 其他因子都和 (θ0,φ0)无关, 所以积分带来的变化体现在c′上, 与阶次2k+1无关, 即不影响高次谐波谱的轮廓.

2 计算结果及分析

本文采用这些参数来计算惰性气体的单原子响应的高次谐波谱: 入射激光的偏振方向是x方向;激光光强为I=5.18×1014W/cm2; 激光的波长为 1 064 nm ; 对应的角频率ω在原子单位下为0.043 a.u.;从而对应的有质动力势能是Up=20ω; 氦原子、氖原子、氩原子、氪原子和氙原子的电离势Ip分别是21.1ω、 18.5ω、 13.4ω、 12ω和 10.4ω; 对于s轨道函数α=2Ip, 对于p轨道函数α=Ip. 采用上面的数据, 本文计算了: ①基态看作是s轨道函数情况下, 由公式(11)计算的氦原子、氖原子、氩原子、氪原子和氙原子所对应的高次谐波谱, 如图1a)所示, 其中, 横坐标为谐波阶次, 纵坐标为谐波强度;②基态看作是p轨道函数情况下, 由公式(15)计算的氖原子、氩原子、氪原子和氙原子的高次谐波谱,如图1b)所示.

综合图1a)和图1b)可见, 两种情况下都表现出了在光电场不变的条件下, 氦原子、氖原子、氩原子、氪原子和氙原子的高次谐波效率随着它们电离势能的减小而依次增大. 这是由于电离势能越大,高次谐波的第一步的电子电离几率越小, 所以谐波效率越小, 截止频率两种情况是一致的, 都符合截止频率为Ip+3.17Up的规律.

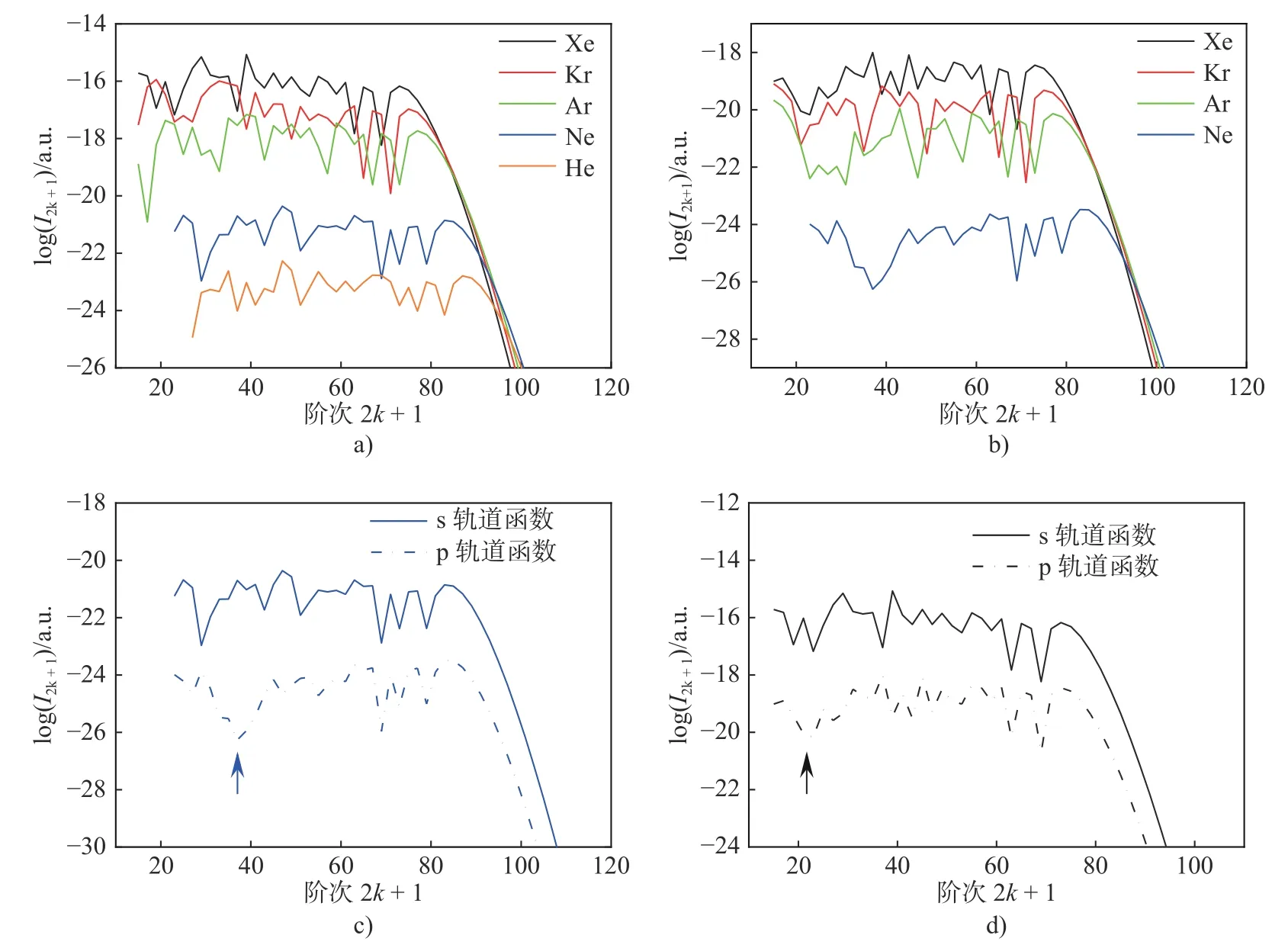
图1 a)以s轨道函数为基函数获得的惰性气体的高次谐波谱; b)以p轨道函数为基函数获得的高次谐波谱;c) Ne原子和d) Xe原子分别以s轨道函数和p轨道函数为基态函数的高次谐波谱的比较Fig. 1 The HHG spectra of noble gases. The ground state wave function is an s orbital function in a) and a p orbital wave function in b); The comparison of the HHG spectra between the above two cases are shown for Ne in c) and Xe in d), respectively

如图1c)和图1d)所示, 对于s轨道和p轨道两种情况下, 高次谐波谱一方面有共同的特征: 相同的截止频率, 在截止频率附近, 有由量子干涉效应引起的局部极小值(如59次谐波). 另一方面轮廓稍有差别: 即p电子产生的高次谐波谱会在平台区额外产生一个凹陷, 对应图1c)和图1d)中用箭头标明的位置, 而s电子产生的高次谐波谱的轮廓没有此凹陷.

下面分析p轨道电子产生的在高次谐波谱上产生凹陷的原因. 我们借用Ne原子的电离势能的数据, 改变p轨道函数的参数α, 给出了不同α下的高次谐波谱, 如图2所示. 由图2可见, 凹陷位置取决于α的大小, 即α越大凹陷越趋向于截止频率的方向. 由图2还可见, 不同的α值情况下的截止频率都是图中黑色虚线所对应的位置, 可见,α值不影响截止频率.

下面将结合三步模型来理解凹陷的根源并通过推导得到它的具体位置.

(1) 三步模型的第一步是电子从基态电离, 式(5)中的因子dx[Pst(t,τ)−Ax(t−τ)]Ecos(t−τ) 可理解为电子在t−τ时刻的电离概率幅, 用g1来表示, 代入式(6)和式(14), 可得

而Pst−A(t−τ)=v(t−τ) 是电离时刻的电子的初速度, 按照三步模型, 电离时刻电子的初速度v(t−τ) 为0. 所以

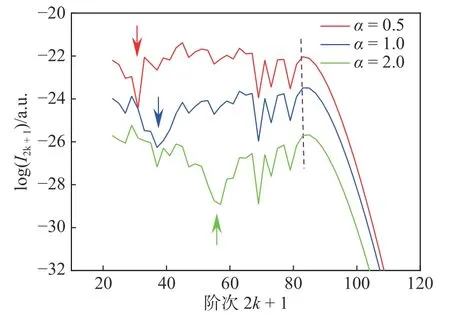
图2 p函数中的取不同 α 值时高次谐波谱Fig. 2 The HHG spectra for different α parameters in a p orbital function

(2) 三步模型的第二步是电子在激光场中自由运动, 获得一相位因子, 用g2表示, 对应式(5)中的e指数因子, 即

同样, 由于Pst−A(t)=v(t), 得到

综合三个步骤, 知电子在t−τ时刻电离, 在t时刻复合, 产生的高次谐波的概率, 即高次谐波的强度正比于

t时刻复合, 产生高次谐波的能量为, 从而有

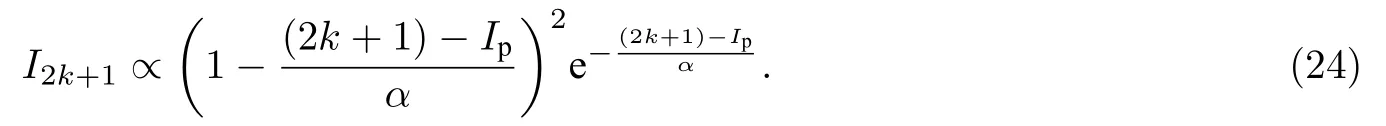
从式(24)可见, p电子产生的高次谐波谱有凹陷, 凹陷的位置对应, 即凹陷处的阶次为

对于氖和氙, 由式(25)估算的凹陷位置分别是37和21, 与图1c)和d)中箭头所示位置吻合. 图2中, 理论估计为27, 37和55, 与箭头所示的凹陷位置也基本相符.

在图3中, 在氖和氙的高次谐波谱中给出了由式(24)计算的结果,可见式(24)基本给出了氖和氙的高次谐波谱的轮廓. 式(23)和式(24)的形式由p函数的在动量空间的微分表达式决定. 所以说, 高次谐波谱的轮廓能看到p函数的在动量空间的微分表达式的特征.

图3 氙原子和氖原子产生的高次谐波谱 (图中的虚线对应式(24)的结果)Fig. 3 The HHG spectra of Xe and Ne (the dash lines from Equation (24) show the respective envelopes)

根据相似的分析, 对于s电子产生的高次谐波的强度应正比于

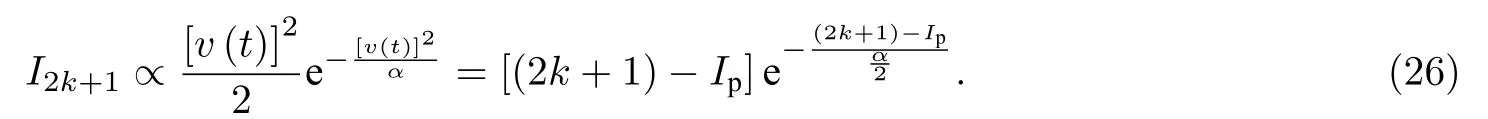
由式(26)可见, s电子产生的高次谐波谱没有凹陷点.

从上面的分析可以知道, 原子或分子中的电子轨道结构特点可以影响高次谐波谱的结构. 对于本文中p轨道造成的凹陷结构, 目前在实验上还没有探测得到: 这一方面可能的原因是单原子响应中其他轨道电子的参与造成的; 另一方面是高次谐波的传输过程中相位匹配也可能导致凹陷现象的不明显. 随着超短激光脉冲技术的不断发展, 原子和分子结构特点对高次谐波产生过程的影响会越来越敏感地体现出来.

3 结 论

本文采用Lewenstein的理论, 分别以s轨道函数为基态函数和以p轨道函数为基态函数, 计算了惰性气体的高次谐波谱; 发现两种情况下得到的高次谐波谱轮廓有差别, 即后者的平台区有一凹陷,而前者没有. 分析表明, 凹陷的位置是由p轨道函数参数α所决定的; 指出了高次谐波的平台轮廓体现了基态函数动量空间的微分表达式的特征. 本文工作可为运用高次谐波分析轨道结构提供参考.

附录A

本附录给出了公式(15)中的Fk(τ) ,C(τ) ,XF5(τ) ,XF3(τ) ,XF1(τ) ,XZ1(τ) ,XZ3(τ) ,XZ5(τ) 的表达式. 具体如下.

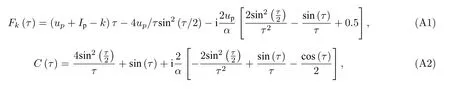
其中,