修正牛顿动力学中的平面圆形限制性三体问题

毕艳芳,王 焘

（华东师范大学 物理与电子科学学院, 上海 200241）

0 引 言

在牛顿动力学和牛顿平方反比万有引力作用下, 二体问题的解是圆锥曲线轨道, 包括广为人知的圆形轨道. 当两个主天体绕其质心做角速度为ω的圆周运动时, 另有一个小天体在同一轨道平面内运动, 就构成平面圆型限制性三体问题. 在以质心为原点、角速度为ω的旋转坐标系中, 3个天体都静止在平衡位置. 在牛顿动力学理论中, 该问题的解给出5个拉格朗日点:L1、L2、L3都与主天体共线,称为直线解或欧拉特解, 其中第一拉格朗日点L1位于两个主天体之间;L4、L5各自与两个主天体构成等边三角形, 称为三角形解或拉格朗日特解. 在给定的雅克比积分下, 希尔曲线即零速度曲线将空间分成希尔域和禁行域两个区域.

作为暗物质理论的竞争对手, 修正牛顿动力学理论[1]巧妙地解释了星系旋转曲线. 修正牛顿动力学理论比牛顿动力学理论函数形式更加复杂, 并且多出一个常数, 通常约定为加速度常数a0. 文献[2]发现, 在153个星系中观测到的2 693个点的径向加速度关系满足统一的函数形式, 加速度常数的最佳拟合值为a0=1.20×10−10m/s2. 修正牛顿动力学理论不仅在星系尺度得到了广泛的研究, 还可以在太阳系内进行检验. 利用日地第一拉格朗日点附近的航天器轨迹[3], 有望精确地检验修正牛顿动力学理论[4]. 到目前为止, 太阳系内修正牛顿动力学理论的研究热点集中在日地第一拉格朗日点, 特别是月球、八大行星对它的扰动. 尚无研究报道该理论中其他拉格朗日点以及平面圆型限制性三体问题的一般性质. 本文将填补这一空白, 在修正牛顿动力学理论中, 较全面地研究平面圆形限制性三体问题,包括雅克比积分、拉格朗日点、希尔曲线和希尔域等, 以最重要的地月系统和日地系统为例, 定量地研究加速度常数对它们的影响.

文献[5]中, Milgram通过动量守恒和位力定理, 得到了修正牛顿动力学极限下圆形轨道中两体力的解析形式. 基于这一结果, 文献[6]给出了修正牛顿动力学理论中的两体相互作用方程

在限制性三体问题中, 第三天体质量m远小于主天体质量M, 可以将式(1)简化成

本文将从这一动力学方程出发, 研究平面圆形限制性三体问题. 当a0取值为 0 时, 修正牛顿动力学就回到了标准牛顿动力学的情形, 这有助于对比和检验计算结果.

本文的后续内容安排: 第1章计算并演示修正的拉格朗日点; 第2章绘制修正的希尔曲线、希尔域和禁行域; 第3章总结全文.

为了计算方便, 本文采用旋转坐标系, 并约定G=ω=J=1, 其中G表示万有引力常数,ω表示旋转坐标系相对于惯性坐标系的角速度,J表示在惯性坐标系中2个主天体相互绕转的角动量. 在这一约定下, 若一个主天体的质量为µ, 则可证明另一主天体的质量为 1−µ. 不失一般性, 本文设µ≤0.5, 在数值计算中, 取地月系统µ= 0.012 195 121 951 2, 日地系统的µ=0.000 002 999 39.

1 修正的拉格朗日点

本文在旋转坐标系下考虑小天体的运动情况. 旋转坐标系相对于两个主天体静止, 且以它们的质心为原点, 记为O(0,0,0). 小天体受两个主天体的共同作用, 其质量远小于主天体质量, 因此不影响主天体的轨道. 记A(−µ,0,0) 、B(1−µ,0,0) 、C(x,y,z) 依次为2个主天体和小天体的位置坐标, 那么, 整个系统的拉格朗日量为

其中,m为小天体质量,分别是小天体到2个主天体的距离. 由拉格朗日方程, 可以得到小天体的运动方程

对于整个系统来说, 拉格朗日点其实就是系统的平衡点, 在这些点上, 小天体或航天器处于平衡状态. 这意味着, 再结合式(4)、式(5)、式(6)得到

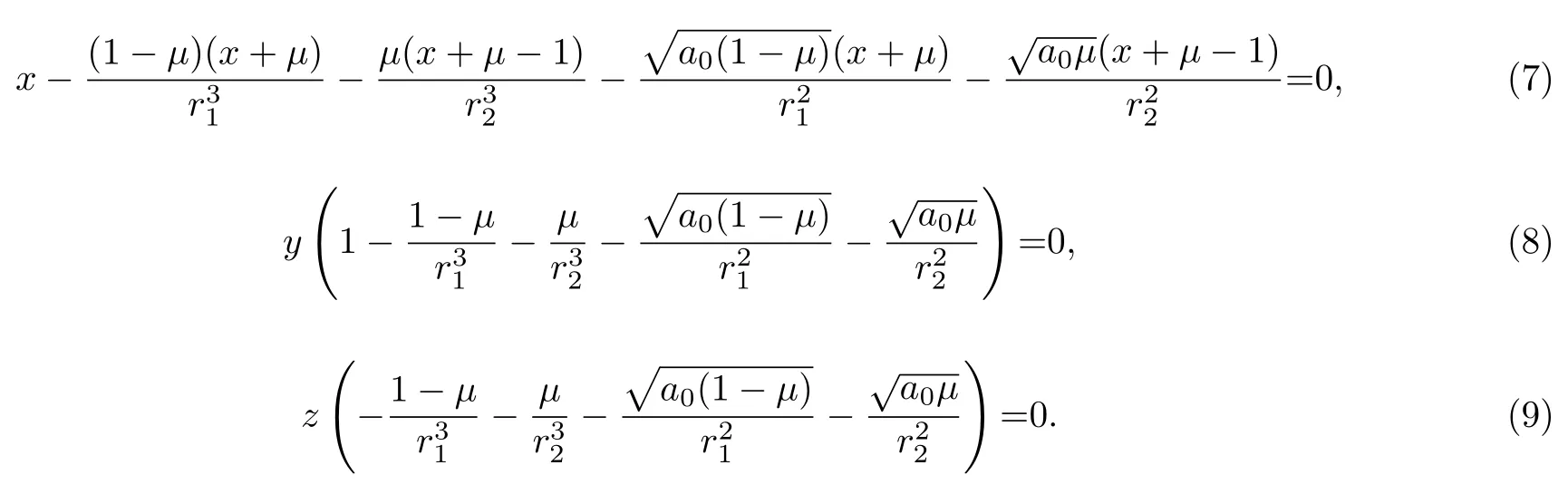
从式(9)不难发现, 要找的平衡点位于Oxy平面内, 此时. 根据式(8), 可以分两种情况进一步求解运动方程.

式(10)说明Oxy平面内可能存在平衡解, 解的数目和具体形式与a0、µ的取值有关.

第二种情况y=0是, 平衡点位于x轴上. 此时有,r1=|x+µ|r2=|x+µ−1|. 联立式(7)、式(8), 得

式(11)有3个解, 就是常说的直线解, 解的x坐标与a0、µ的取值有关.

利用式(10)、式(11), 在地月系统和日地系统中进行数值计算, 就可得到不同参数取值下的拉格朗日点. 图1与表1展示了本文的计算结果. 图1与表1的左列对应地月系统, 右列对应日地系统.在每一列中, 从上到下a0的取值依次为0、0.001、1、1 000. 表1中ρALi和ρBLi分别以1个地月距离(约384 404 km)和1个日地距离(约14 959 787 km)为单位.

值得注意的是, 图1中有些情形没有L4点和L5点, 可以利用式(10), 通过估算来理解这一特点.根据式(10), 可以得到

当µ≪a0时, 还可以根据式(10)得到

图1 拉格朗日点分布图Fig. 1 Maps of the Lagrangian points

将式(13)和式(14)分别代入式(12)的分子和分母, 可以发现

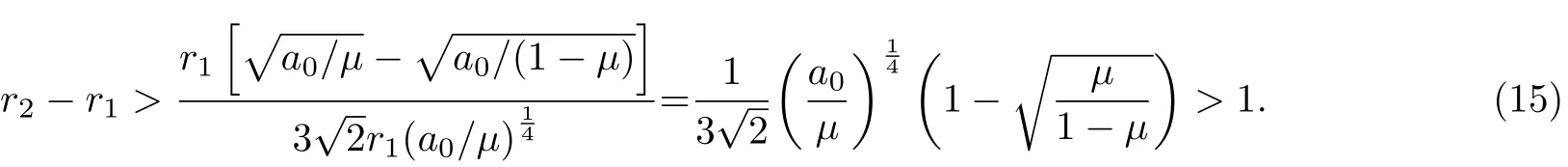
2 修正的希尔曲线和希尔域

如果定义那么运动方程(4)、(5)、(6)可以记成x¨−2y˙=∂U/∂x,y¨+2x˙=∂U/∂y,z¨=∂U/∂z. 由此可知, 降阶后的运动学方程满足x˙2+y˙2+z˙2=2U−C. 对于给定的雅克比积分C, 小天体的运动限制在一个固定的曲面上, 这个曲面就是零速度曲面, 满足x˙2+y˙2+z˙2=0. 零速度曲面可以用来界定希尔域和禁行域. 如果只考虑二维平面的运动, 这些轨迹就表现为一系列曲线, 就是零速度曲线, 也称希尔曲线[7].

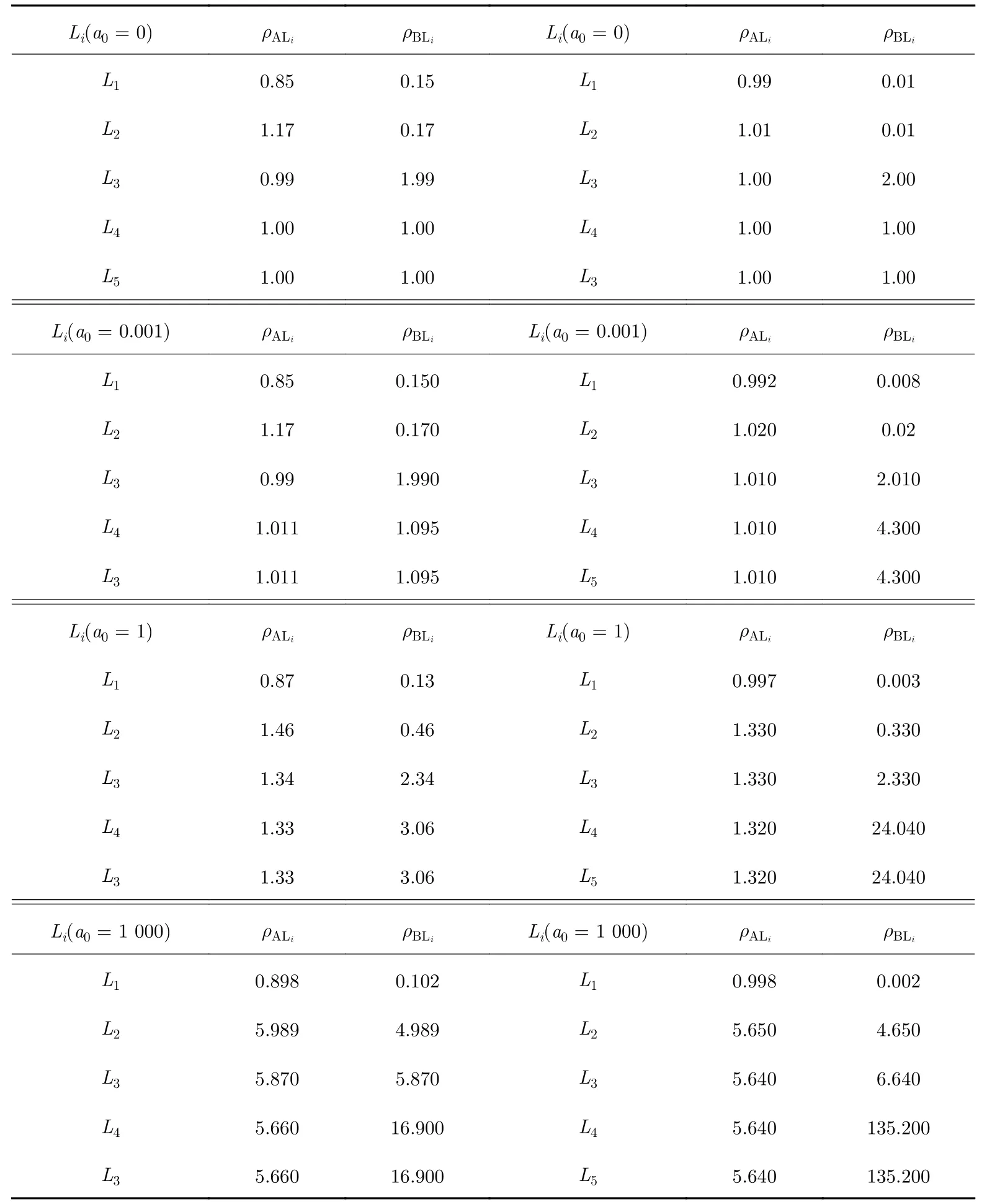
表1 拉格朗日点与主天体的距离Tab. 1 The distances between the Lagrangian points and the main celestial bodies

本文仍以地月系统和日地系统为例, 绘制不同雅各比积分下的零速度曲线组合成的等高线图, 进而分析a0对小天体运行轨迹的影响. 图2中各子图的参数取值与图1、表1一致, 左列对应地月系统,右列对应日地系统. 在每一列中, 从上到下a0的取值依次为0、0.001、1、1 000. 在每个子图中, 不同的等高线对应不同雅各比积分时的零速度曲线.

图2 不同加速度常数下的等高线图Fig. 2 Contour maps for different acceleration constants

3 总 结

本文在修正牛顿动力学理论中重新研究了平面圆形限制性三体问题. 这些研究结果表明, 在修正牛顿动力学理论中, 平面圆形限制性三体问都都有朗格朗日点. 在牛顿动力学极限下, 即a0=0 的时候, 3个直线解位于主天体所在直线上, 另外2个点与2个主天体构成等边三角形. 同一系统, 随着a0取值的增大, 拉格朗日点的位置与牛顿动力学情况下的区别就越明显, 甚至在某些参数区域只有直线解.

本文的研究结果还表明, 对于确定的系统来说,a0值的差异会对小天体运动区域有所影响. 图 2表明, 在a0很大的时候, 修正牛顿动力学理论与经典牛顿理论的零速度曲线分布有较大差异. 具体表现为, 随着a0的增加, 系统之间的希尔域不再连通, 即地月系统小天体很难靠近月球, 日地系统小天体则很难靠近地球.

本文得到的拉格朗日点均为µ和a0取值确定下的数值解, 具体到不同的系统, 拉格朗日点位置和数目有所不同. 由于篇幅所限, 本文未能研究这些拉格朗日点的稳定性. 本文注意到, 在修正牛顿动力学理论的平面圆形限制性三体问题中, 三角形解并不总是存在的; 相应临界线上,µ和a0的参数值也是一个值得进一步研究的问题.