基于自适应空间正则化的视觉目标跟踪算法
2021-02-06谭建豪张思远
谭建豪 张思远
(湖南大学电气与信息工程学院 长沙 410082)(机器人视觉感知与控制技术国家工程实验室(湖南大学) 长沙 410082)(tanjianhao@hnu.edu.cn)
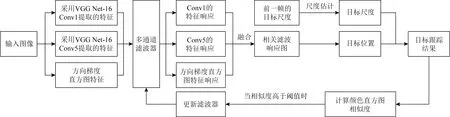
Fig. 1 Flow chart of tracking algorithm图1 跟踪算法流程图
视觉跟踪技术是计算机视觉领域中一个重要的研究方向,在视觉制导、人机交互、视频监控等多个领域都有广泛应用.随着MOSSE(minimum output sum of squared error)算法将相关滤波引入视觉跟踪中,这种从时域计算转换到频域计算的方法大大提升了运算速度.基于相关滤波的视觉跟踪技术由此得到迅速发展[1],出现很多经典的跟踪算法,如Henriques等人[2]提出的核相关滤波(kernelized correlation filter, KCF)算法,速度在CPU上达到172fps;Danelljan等人[3]提出的DSST(discriminative scale space tracking)算法,采用了33种不同尺度,大大提高了尺度估计的精度;Li等人[4]提出的SAMF(scale adaptive with multiple features)算法,引入了多特征融合和尺度自适应策略,对遮挡具有良好的抵抗能力.
而随着相关滤波类视觉跟踪算法性能的不断提升,因循环移位采样导致的边界效应问题引起了学者的关注.边界效应产生的错误样本会导致模型判别力下降,尤其是在目标快速变形和快速运动的场景下更为明显.为解决这一问题,Galoogahi等人[5]提出了BACF(background-aware correlation filter)算法,使用真实的负样本代替正样本循环移位生成的负样本,这些样本包括了更大的搜索区域和真实的背景,取得了不错的效果;Danelljan等人[6]提出了SRDCF(spatially regularized discriminative correla-tion filters)算法,在模型中加入了空间正则化项,让边界附近滤波器系数接近零,一定程度上缓解了边界效应问题,但该方法为了形成合适的正则化权重,必须仔细调整一组超参数,否则会导致较差的跟踪性能,且算法整体速度较慢;Dai等人[7]提出了基于自适应空间正则化的ASRCF(adaptive spatially-regularized correlation filters)算法,此算法可以学习到空间正则化权重的变化,对非目标区域的惩罚更为准确,但在遇到目标有较大形变时,滤波器对不准确目标的学习容易导致跟踪漂移;Li等人[8]提出了基于时空正则化的STRCF(spatial-temporal regularized correlation filters)算法,利用时间正则化来建立相邻滤波器之间的关系,但空间正则化权重没有学习能力,在遇到相似背景干扰时跟踪容易发生漂移.
为此,本文提出了一种基于自适应空间正则化的视觉跟踪算法,该算法通过建立正则化权重在相邻帧之间的关联,降低算法模型在处理不准确样本时发生过拟合的风险,减小边界效应的影响;采用一种自适应宽高比的尺度估计策略,灵活适应目标宽高尺度比的变化;利用基于颜色直方图相似度的模型更新策略,阻止模型在跟踪不准确时进行更新,降低模型漂移风险.
1 基于自适应空间正则化的视觉跟踪算法
1.1 算法整体流程
本文提出的基于自适应空间正则化的视觉跟踪算法流程如图1所示.算法的主要步骤为:
1) 根据第1帧图像中标记的跟踪目标训练滤波器;
2) 提取输入图像的方向梯度直方图(histogram of oriented gradients, HOG)特征,并利用VGG Net-16的Conv1和Conv5分别提取图像浅层和深层特征;
3) 提取的特征与滤波器进行相关运算,得到多个特征响应,经过融合得到相关滤波响应图,进而获取目标位置;
4) 利用自适应宽高比的尺度估计方法得到目标尺度;
5) 判断估计的目标与前一帧目标颜色直方图相似度是否高于阈值,若满足,则进行滤波器更新,否则不更新滤波器.
1.2 自适应空间正则化模型
经典的相关滤波模型采用循环移位的方式进行采样,虽然大大提高了样本数量但也带来了边界位置周期性重复的问题,导致模型使用了一些非真实样本进行训练.同时,由于正样本周围不可避免地包含一些背景信息,在训练过程中分类器容易将这些紧邻目标的背景视作目标进行特征学习,降低了整体的跟踪性能.为解决这个问题,本文提出一种引入自适应空间正则化的算法模型.在经典的相关滤波模型中引入自适应空间正则化项,通过建立正则化权重在相邻帧之间的关联,自适应调整模型的正则约束.目标函数定义如式(1):
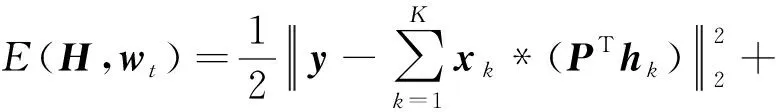
(1)
其中,X=(x1,x2,…,xK)是用于训练的样本数据,H=(h1,h2,…,hK)表示滤波器.y是预期的高斯响应,P是二元对角矩阵,用于使相关算子能直接应用于真实前景和背景样本.*表示卷积运算,⊙表示哈达玛积.λ1和λ2是空间正则化参数,wt是第t帧(当前帧)需要优化的自适应权重,wt -1是第t-1帧(前一帧)的自适应权重.初始时,将w0设为负高斯形的分布,之后根据目标的变化学习更准确的权重.根据帕塞瓦尔定理,将目标函数转换到频域中,并转换为如式(2)的等式约束优化形式,以方便进一步地求解.
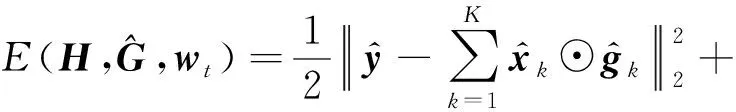
(2)

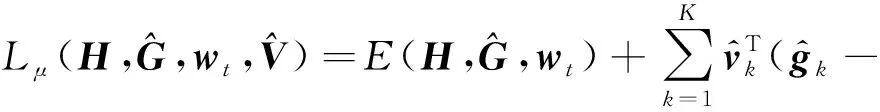
(3)
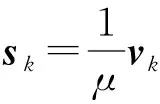
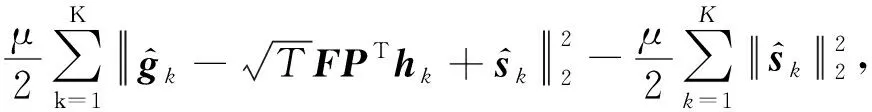
(4)
其中,S=(s1,s2,…,sK).对式(4)采用方向交替乘子法(alternating direction method of multipliers, ADMM)来求解,即迭代求解以下子问题:
1) 求H的最优解H*.
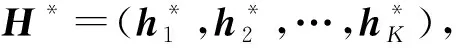
(5)
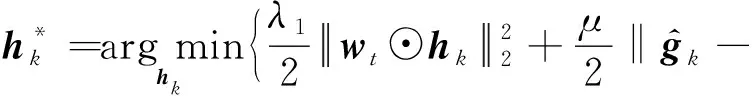
(6)
其中,W=diag(wt),p=(P11,P22,…,PTT)T是矩阵P中对角元素组成的列向量.
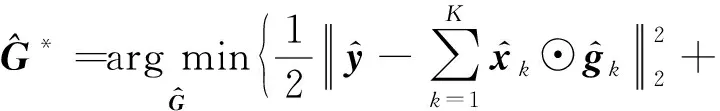
(7)
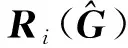
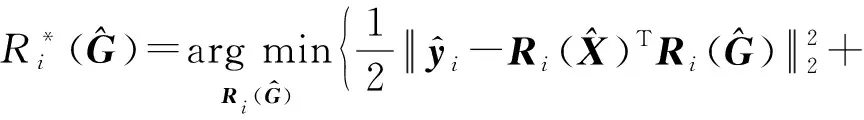
(8)

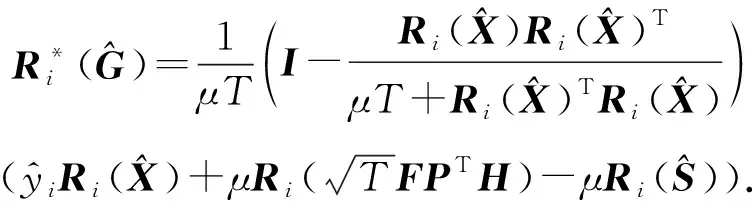
(9)
3) 求wt的最优解wt*.
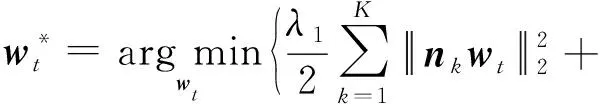
(10)
其中,nk=diag(hk).
4) 更新拉格朗日乘子.

(11)
通过反复执行上述4个步骤来进行优化,待到收敛后,可获得一组最优的滤波器和空间正则化权重.
1.3 自适应宽高比的尺度估计
尺度金字塔方法是视觉跟踪中常用的尺度估计策略,其基本原理是将原有的目标框尺度进行不同比例地放大和缩小,并计算对应的响应,选择响应值最大的作为跟踪目标框,从而达到尺度自适应追踪.在实际跟踪任务中,目标的宽高比可能发生大的变化,这时尺度金字塔方法的缺点就凸显出来:无法适应目标宽高尺度比的改变,导致跟踪变得不再精准,经过多帧以后出现模型漂移,极易导致目标完全跟丢.
针对这一问题,本文提出一种自适应宽高比的尺度估计策略:保持前一帧预测目标的高不变,以前一帧的宽乘以n个不同的缩放因子作为候选宽,组合得到n个候选尺度;根据这些候选尺度来提取图像块,并获得每个图像块对应的HOG特征描述;与滤波器进行相关运算后,对输出响应进行排序,取前q名的宽尺寸作为新的候选宽尺度;以前一帧的高乘以m个不同的缩放因子作为候选高,组合得到q×m个新的候选尺度;根据这些新的候选尺度提取图像块,并提取每个图像块对应的HOG特征描述;再次与滤波器进行相关运算后,取响应最大的图像块作为当前帧的预测目标图像,其对应的尺度即为当前帧的预测尺度,如图2所示.使用该策略能灵活适应目标宽高比的变化,在发生形变、旋转等情况时仍保持良好的跟踪精度.

Fig. 2 Schematic diagram of scale estimation图2 尺度估计示意图
1.4 基于颜色直方图相似度的更新
相关滤波类视觉跟踪算法中的更新策略一般有2种:一种是对每一帧都进行模型更新,这样能保证模型很好地适应目标的形变,但存在模型漂移的问题[9-12];另一种是每间隔一段时间更新一次,这样的好处是能一定程度上减少计算量和抑制模型漂移[13],但若目标在短时间内发生大的形变,这种更新策略会使模型难以准确跟踪目标.
本文采用一种基于颜色直方图相似度的更新策略,其主要思想是:利用颜色直方图相似度的大小来判断是否更新模型,仅当预测的目标和前一帧目标的颜色直方图相似度高于设定阈值时,才进行模型更新.当前,巴氏距离在相似性度量方面的研究已经十分成熟,尤其在直方图相似度计算时,巴氏距离获得的效果最好,因此本文中通过计算2帧图像颜色直方图概率分布之间的巴氏距离来判断2帧图像的相似性.巴氏距离越小,则颜色直方图相似度越高.计算颜色直方图相似度时,对彩色图像分为红(red,R)、绿(green,G)、蓝(blue,B)3个颜色通道分别计算相似度,每个通道都以8等分进行像素划分,最后取3个通道的平均值作为最终的相似度.对灰度图像则只进行灰度值的直方图相似度计算,同样划分为8等分.采用这种基于颜色直方图相似度的更新策略能阻止模型在跟踪不准确时进行更新,防止模型漂移,并在一定程度上提高算法运行速度.

Fig. 3 Success plots of OPE图3 OPE成功率比较
2 实验结果分析
2.1 实验环境与参数设置
实验采用英特尔酷睿i5-8300H处理器,内存为16 GB,操作系统环境为64位Windows10系统.基于MATLAB R2016a软件平台及工具箱MatConvNet实现程序编写.
浅层网络提取的特征有较高的分辨率,有利于对目标进行精准地定位,而深层网络提取的特征则包含更多的语义信息,鲁棒性更强.故实验中利用VGG Net-16 Conv1提取的浅层特征,VGG Net-16 Conv5提取的深层特征和HOG特征进行对象表示.由正则化的基本原理可知正则化参数太小则无法消除模型的过拟合,太大容易产生欠拟合,经过多次实验调整,本文将正则化参数分别设置为λ1=0.1和λ2=0.001.模型的学习率通过迭代实验的方式进行调整,最终设置为0.015.交替方向乘子法优化过程使用3步迭代.设置尺度相关因子时,考虑到尺度跟踪因子的值和计算量呈正相关,为保证算法速度,尺度跟踪因子不宜取过大的值.本文尺度跟踪因子设置为n=m=5,设置q=3.通过多次调整实验,将缩放增量设置为0.08.
本文分别在UAV123[14],OTB2013[15],OTB 2015[16]这3个公开数据集上对跟踪算法进行测试和对比.其中,UAV123是由低空无人机捕获视频组成的数据集,共包含123个视频序列;OTB2013数据集由51个视频序列组成,其中包含一定量的灰度序列;OTB2015数据集由100个视频序列组成,其中包含多种视觉跟踪过程中可能出现的复杂情况,能较为全面地评估算法的整体性能.
2.2 结果与分析
在2.1节所述的实验设置下,本文提出的跟踪算法跟踪速度平均为17.15 fps.实验中,使用一次通过评估(one-pass evaluation, OPE)的方式,对本文提出的算法(our)进行性能评估,并与DSST[3],SAMF[4],BACF[5],SRDCF[6],ECO-HC(efficient convolution operators with hand-crafted feature)[17],Staple(sum of template and pixel-wise learners)[18],Staple_CA(Staple with context-aware)[19]这7种目前跟踪效果领先的相关滤波类算法进行对比,生成成功率曲线图和精确度曲线图.在此基础上,对算法进行成功率和精确度排序,其中成功率排序的依据是成功率曲线下面积(area under curve, AUC),精确度排序的分数阈值设置为20像素.评估结果分别如图3和图4所示,本文所提出的跟踪算法在UAV123,OTB2013,OTB2015数据集上的成功率得分分别为:0.484,0.658,0.652,精确度得分分别为:0.656,0.863,0.855,排名均为第1.较排名第2的ECO-HC算法在成功率上平均提升了3.12个百分点,精确度上平均提升了1.36个百分点.图3和图4显示各算法在UAV123数据集上的成功率和精确度明显低于OTB2013,OTB2015,这是由于UAV123数据集中的视频序列都是无人机在空中拍摄的,目标较小,角度更多,跟踪难度相对更大.尽管如此,本文提出的算法在该数据集上的表现依旧优于其他7种算法,进一步验证了本算法的有效性和可靠性.

Fig. 4 Precision plots of OPE图4 OPE精确度曲线图
为更全面地分析所提出的算法的性能,本文还在OTB2015数据集上测试了上述8种算法在快速运动、运动模糊、目标形变、光照变化、平面内旋转、目标遮挡、平面外旋转、出视野、尺度变化、背景杂乱和低分辨率这11种复杂场景下的跟踪成功率,结果如图5所示.
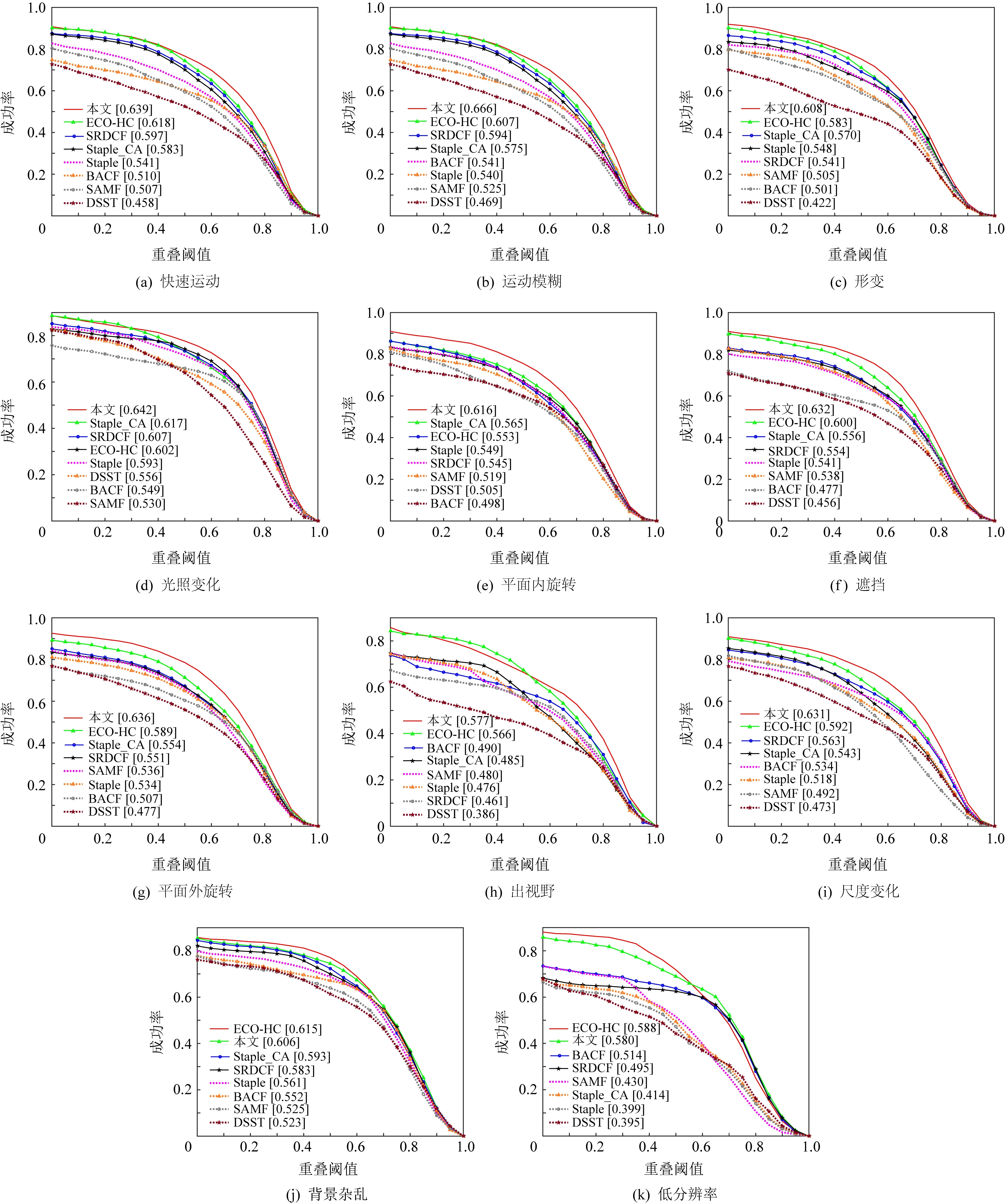
Fig. 5 Success plots in 11 complex scenes图5 11种复杂场景下的成功率曲线图
由图5可知,本文所提出的算法在快速运动、运动模糊、形变、光照变化、平面内旋转、遮挡、平面外旋转、出视野和尺度变化这9种复杂场景下的跟踪成功率均高于其他算法.在背景杂乱和低分辨率2种场景下,本文提出算法跟踪成功率排名第2.为更直观地分析本文算法在各场景下的性能,计算本文算法在各个场景下相对其他算法中排名最佳的一种的性能提升百分点,具体数据见表1.由表1可知,本文算法在运动模糊和旋转场景下的成功率提升相对更大,分别提升9.72个百分点、9.03个百分点(平面内旋转)和7.98个百分点(平面外旋转),说明本文提出的跟踪算法对运动模糊和旋转带来的干扰有更强的抵抗力,能有效减少跟踪过程中的模型漂移,提高复杂场景下跟踪的准确性和稳定性.对于尺度变化场景,本文算法成功率提高了6.59个百分点,说明自适应宽高比的尺度估计策略能更好地跟踪目标的尺度变化.
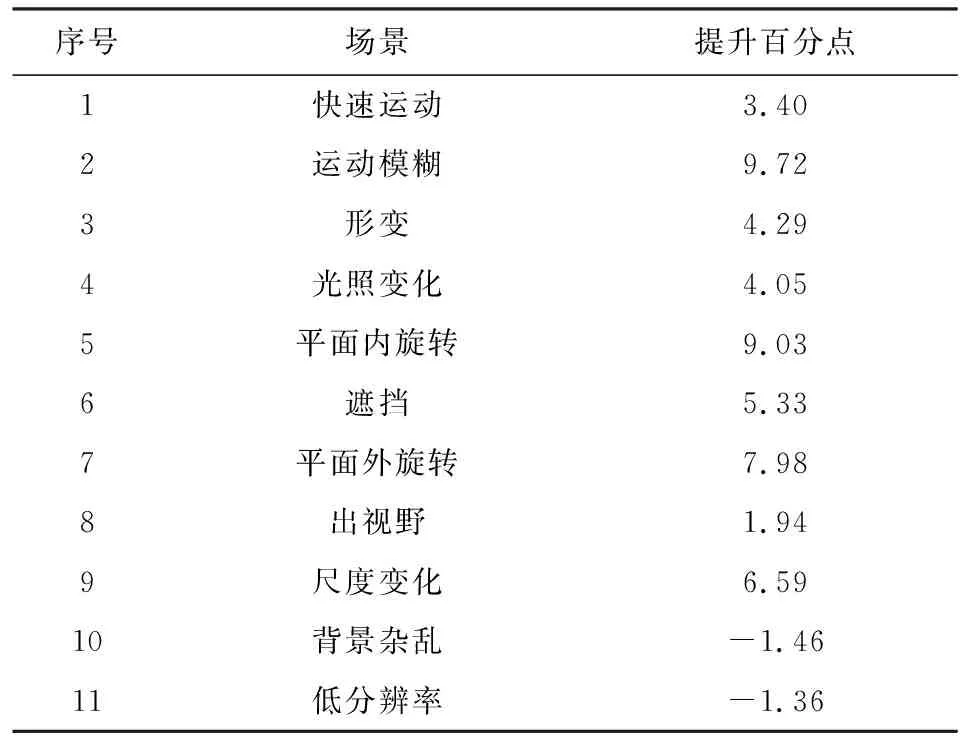
Table 1 Improvement of Algorithm Success Rate inVarious Scenes
图6为综合排名领先的4种算法(本文,ECO-HC,Staple_CA,SRDCF)对部分复杂场景序列跟踪结果,可以看到在这4种复杂场景下,本文算法都有良好的表现.在对Biker序列跟踪到第100帧时,只有本文算法和ECO-HC算法能在目标快速抖动并转向后依旧保持准确跟踪,其余2种算法模型已经漂移到其他位置,无法再进行正常跟踪;对Diving序列进行跟踪时,其他采用固定的宽高比估计的算法都在形变过程中逐渐丢失了目标,只有本文算法一直保持着跟踪;对Girl2序列跟踪到第790帧时,女孩被遮挡后再次出现,只有本文算法和ECO-HC算法能重新定位到目标,但本文算法定位得更精准;对Liquor序列跟踪到第890帧时,一直表现良好的ECO-HC算法已经完全漂移到干扰物体上了,而此时本文算法的定位准确度也略低于SRDCF算法.由此可见本文提出的算法对大部分复杂场景具有较好的适应性,但在出现与目标相似的干扰时跟踪准确性会略有下降.

Fig. 6 Tracking results of some complex scene sequences图6 部分复杂场景序列跟踪结果
3 结 论
针对相关滤波类视觉跟踪算法中存在的边界效应问题,本文提出一种基于自适应空间正则化的视觉跟踪算法,在经典滤波模型中引入了自适应空间正则化项,建立正则权重在相邻帧之间的关联,从而自适应调整当前帧的模型正则化权重,有效缓解了边界效应的影响;使用自适应宽高比的尺度估计策略,提高了复杂场景下尺度估计的准确性;采用基于颜色直方图相似度判别的模型更新策略,抑制模型漂移并加快跟踪速度.多个数据集上的测试结果表明,本文提出的算法的整体跟踪精确度和成功率均优于对比的其他算法,验证了算法的有效性.11种复杂场景下的针对性实验表明,该算法能够较好地实现在快速运动等多种复杂情况下的目标跟踪,具有较强的适应性.但该算法在背景杂乱和低分辨率场景下的目标跟踪不够稳定,未来将对此展开进一步研究.
