基于持久性内存的单向移动B+树
2021-02-06张兴军纪泽宇董小社姬辰肇
闫 玮 张兴军 纪泽宇 董小社 姬辰肇
(西安交通大学计算机科学与技术学院 西安 710049)(yanweiwei.002@stu.xjtu.edu.cn)
由新型非易失存储介质如PCM[1],ReRAM[2],MRAM[3]等构成的持久性内存(persistent memory, PM)具有按字节访问、非易失、存储密度高等特性,为计算机主存与外存融合提供了一个强大的契机.相较于传统内存,PM由于内部结构与制作工艺不同,具有更强的扩展性,同时由于其持久化特性,PM还能够大幅降低系统的静态能耗.相较于传统块设备,PM能够提供更快的访问速度,同时支持按字节访问.
为了大幅提高数据访问速度,存储系统通常需要根据访问需求及硬件特性设计高效的索引结构如树、散列、字典树等.B+树以其扩展性好、性能稳定、缓存局部性较强等特点成为其中最受欢迎的索引结构之一,目前作为内存数据结构也得到了广泛应用.然而PM的出现并作为存储级内存设备为其设计带来了新的挑战:
1) 失败原子性问题.目前常见Cache由易失存储介质构成,在系统故障后数据会完全丢失.因此在写回式(write-back)Cache与PM交互时,cache line内数据会根据Cache替换算法被写回到主存上,若发生故障,Cache内未及时写回到PM中的数据将会丢失.这可能会破坏PM中数据的完整性.另外为了满足内存级并行[4-5],Cache中写回PM的cache line的顺序可能被打乱,进一步增加了数据恢复的难度.为了保证失败原子性,目前常见操作是使用clflush指令将cache line显式写回到主存之上,同时通过mfence指令规定cache line的写回顺序.然而上述操作会显著降低内存的并发性能,进而降低整个系统的性能.
2) 持久化开销问题.保证失败原子性会带来显著的持久化开销(mfence+clflush),这个开销在B+树中会被进一步放大,如若B+树节点内数据有序,那么插入一个数据的排序操作会引起平均一半数据的移动,这些移动有明确的移动次序,意味着多次有序持久化操作;若B+树内节点无序,需先持久化数据,再持久化相应元数据;B+树节点的合并与分裂时,涉及到大量数据移动(拷贝)与部分指针的修改,数据移动(拷贝)必须在指针修改之前完成;若采用写时复制策略,亦涉及到大量数据移动(拷贝)与部分指针的修改.同时目前商用较为成功的持久性内存如Intel Optane DC persistent memory亦面临着使用寿命有限的问题[6-8],过多的持久化操作亦会影响其设备的使用寿命.
虽然现存PM设备相较传统DRAM,延迟与吞吐量存在一定差距[9-10],但随着新型非易失存储介质技术的不断发展,其性能差距必然会被不断缩小(ReRAM具有近似SRAM的性能).同时在官方公布信息与文献[10]针对Intel Optane DC persistent memory的测评中均无法得知其失败原子性的保证粒度及机制,因此本文假定PM的失败原子性保证仍为8 B.本文聚焦基于单一PM架构的B+树设计,旨在保证数据结构失败原子性的基础上,进一步减少持久化开销,进而提高其性能并优化其使用寿命.
本文设计主要基于以下4个观察:
1) 使用无序数据布局能够大幅提高写入性能,但由于数据无序,查找速度会受到很大影响,同时也会影响插入操作中节点内元素定位的过程.通过添加元数据加快查找速度会带来额外的持久化开销.节点内数据排序能够大幅提高数据访问性能,但排序开销较大.
2) B+树节点占用率通常为70%左右[11].
3) 在有序节点内,插入或删除一组数据会造成平均50%的数据移动,这将带来大量的有序持久化操作.
4) 同节点内,插入操作能够大概率与之前发生的删除操作结合,进而减少数据的移动距离.
本文针对有序节点进行优化,主要贡献包括3个方面:

Fig. 1 Updating the node with three strategies图1 节点的3种更新方法
1) 设计了一种基于节点内数据真实分布的数据单向移动算法.通过原地删除的方式,减少删除带来的持久化开销.利用删除操作在节点内留下的空位,减少后续插入操作造成的数据移动,进而减少数据持久化操作数量.
2) 基于该单向移动算法,设计了一个基于PM的单向移动树(one-direction shifting tree, ODS-Tree).ODS树通过基于数据分布的分裂算法缓解了节点空间利用率较低的问题,同时利用选择性重均衡算法进一步节省了ODS树占用的空间.
3) 通过单一负载与混合负载验证本文所提出的ODS树空间利用的合理性及访问性能.
1 研究背景
1.1 节点更新方式
目前常见B+树节点更新的方式如图1所示,包括原地更新(in-place updates)、日志式更新(log-structured updates)和写时复制(copy-on-writes, COW).具体介绍如下:
1) 原地更新.原地更新是指增删查改等操作直接作用于原始节点.如图1(a)所示,插入操作直接发生在节点内,该过程需要日志来保证更新的原子性,同时更新操作需要的空间较少.
2) 日志式更新.如图1(b)所示,增删查改等操作均记录在日志内,以追加的方式存储在节点之后,或存储在特定区域.该更新策略能够支持高效的顺序读写,因此非常适合基于传统机械硬盘的存储.日志式更新由于其产生的日志式结构,不需要额外日志保证原子性,但读操作需要访问原节点以及其所有日志并通过一定的计算才能获得正确结果.
3) 写时复制.如图1(c)所示,当我们要对节点进行更新时,首先分配一个新的节点,将原始节点数据拷贝到新节点中,然后将相应更新操作在新节点内进行,更新完成后,通过修改父节点内指针使新节点替换原始节点.写时复制不需要额外日志保证更新的原子性,但会引起显著的写放大,在树结构中尤为明显,如产生一个“自底而上”的拷贝.
文献[12]中通过对比分析在PM环境下的3种更新策略,提出原地更新方式更适用于基于PM的B+树节点更新.在原地更新条件下,由于节点内数据排布方式不同,增删查改等操作细节也需要相应的变化.
1.2 节点数据排布方式及其更新方式
树节点内常见数据排布方式包括有序排布与无序排布.有序排布是指所有数据按照数据key的大小升序或降序排布,这有利于查找速度的提升,但插入操作会造成大量的数据移动(平均一半节点内数据),删除操作与插入操作类似,只是数据移动方向相反.无序排布是一种写优化排布,在此排布下插入操作直接将数据存储到数据组尾部(或数据组内部可用位置),删除操作将数据组内相应数据删除或在数据组尾部存储一个带删除标记的该数据.无序排布的写性能较高,但每次访问某一数据都需要遍历所有数据,造成大量的查找开销,写性能优势亦会相应下降,可以通过元数据设计优化降低查找开销.
1.3 失败原子性及其保证
原子性通常可分为并发原子性与失败原子性.并发原子性是指我们对数据的操作在多个事务看来具有原子性,这意味着任何事务无法看到操作过程中数据的中间状态.目前保证并发原子性的常见机制除利用显式内存屏障外还可通过硬件事务内存保证[13-14].
失败原子性是指在数据持久化的过程中,需要保证断电或系统故障后数据的完整性与正确性.其中一个破坏失败原子性的主要表现为数据从易失介质写入到非易失介质的过程中,若传输数据量大于非易失介质的原子写入粒度,此过程中发生断电或故障,未写入数据将会丢失,同时非易失介质内数据可能会出现无法识别的局部更新现象.在基于PM的存储系统中,Cache与PM的交互粒度为一条cache line(通常为64 B),原子性更新粒度为8 B.因此故障既可能发生在单条cache line内字(word)更新之间(在64位处理器中,word长度通常为8 B),也可以能发生在多条cache line更新之间,同时由于粒度差距,日志会造成显著的写放大.结合图2分析,失败原子性的保证条件为:
1) 若需要更新的数据量小于等于8 B,则可直接对数据进行更新操作.
2) 若需要更新的数据大小大于8 B小于等于64 B且位于一条cache line内,则需考虑在当前cache burst order(word写回顺序)情况下[15],持久化一条cache line过程中发生故障是否会破坏数据的完整性.若单条cache line内所有word不存在依赖性,则需使用日志保证所有word在一个原子区间内完成持久化操作(不考虑额外硬件保证).若word之间存在依赖性(原地更新场景下插入操作后数据移动),为减少日志开销,可通过选择特定的burst order通过一次持久化指令保证word有序持久化到PM上.
3) 若需要更新的数据大于8 B且跨多条cache line,则在每条cache line内需满足条件2).同时由于多条cache line写回PM过程中可能会出现乱序问题,因此还需要保证多条cache line的写回顺序.若cache line之间不存在依赖性,则多条cache line的更新需保证在一个原子区间内完成,通常采用日志方式完成(不考虑额外硬件保证);若多条cache line之间存在依赖性(原地更新场景下插入操作后数据移动),为保证多条cache line之间的有序持久化,需要采用显式持久化指令+内存屏障的形式,保证多条cache line顺序持久化到PM上.

Fig. 2 Updated data after insertion under different conditions图2 不同条件下插入操作更新的数据量
在B+树中,更新操作通常仅修改value值,而value值的长度通常为8 B,插入操作需完成一次key,value对的插入,尺寸大于8 B.在节点内数据有序排布的情况下,更新操作能够直接对数据进行原子更新操作;插入操作会造成大量的数据移动(平均移动节点内一半的数据),这涉及到大量数据的修改,操作粒度通常远大于原子更新粒度,同时数据在移动过程中存在依赖性,因此需根据更新数据量大小选择2)或3)来保证失败原子性,即保证被更新数据的有序持久化.删除操作与插入操作类似,仅移动方向相反.由于节点内数据有序排布,查找操作可以通过顺序查找或二分查找进行,查找性能较高.
在节点内数据无序排布的情况下,更新操作可直接对原始数据进行.插入操作会将key,value对追加到尾部(或数据组内部可用位置),结合2)分析,该操作需要日志保护.但我们可以通过增加一个额外的位图表示数据的可见性,数据写入后,通过原子性更新位图来保证整个追加操作的原子性,另外也可通过该位图来快速完成删除操作(标记位图相应位置为0即可,无需在数据组尾部追加标记).基于上述条件优化之后,插入操作的持久化保证可简化为先持久化key,value对,再持久化元数据(位图).查找操作需要遍历所有有效数据,若数据存储设备与Cache直接交互,位图虽然能减少查找开销,但访存开销依旧较高.
如果更新数据量小于8 B,更新操作可以直接原子性完成,更新数据量大于8 B则需要根据情况选择持久化策略:在有序节点内,若更新操作仅涉及修改一条cache line,则需保证cache line内每一个word的持久化顺序,若更新涉及到多条cache line,则需要保证数据移动过程中相应修改的cache line按一定顺序持久化;在无序节点内,需要先持久化数据,再持久化元数据.因此可得到结论:无论节点内数据如何排布,更新大于8 B的失败原子性均需要通过有序的持久化操作来保证.
目前基于X86架构下,保证数据持久化的常用指令包括clflush,clflushopt,clwb[16].clflush能够显式地将一条包含指定地址的cache line写回到内存中同时使Cache中相应的cache line无效;clflushopt是一种并行版本的clflush;clwb在clflushopt功能的基础上,能够保证cache line在Cache中有效,进而能够在一定程度上保证Cache的命中率.为了保证数据持久化操作之间的有序性,我们可以通过mfence指令来规定持久化的顺序,目前相关研究均假定clflush与store,clflush指令存在乱序现象,但最新Intel编程手册中指出clflush不会与上述指令乱序.由于mfence添加与否对本研究影响极小,为便于对照,故本研究采用clflush+mfence的方式保证数据有序持久化操作.为了进一步提高数据持久化效率,文献[17]提出了epoch barrier,通过硬件保证多个epoch之间的持久化顺序,同时epoch内flush操作可以并行执行.文献[18]在epoch barrier的基础上,通过使strand内epoch可并发执行,进一步放松了持久化操作的顺序性.由于实验硬件条件限制,同时结合前人研究,本文采用clflush与mfence指令保证失败原子性.
除单个节点内情况外,B+树的重均衡操作也会带来大量的持久化操作,因此亦需要保证其失败原子性.B+树的分裂操作原子性保证与写时复制相似,但是由于B+树为了支持高效范围查找,叶子节点间通过兄弟指针连接,这将导致一个新节点插入到树中需要修改2个指针(父节点内指针与兄弟节点内指针).B+树节点合并操作亦涉及到上述2个指针.这将增大基于PM的B+树的设计难度.
1.4 相关研究
为了减少基于PM的B+树持久化开销,目前相关研究根据存储架构不同可分为:基于DRAM+PM的B+树与基于单一PM架构的B+树.基于DRAM+PM架构的部分主要相关研究如下:
1) NV-Tree[19].内部节点数据有序且存储在DRAM内,该设计能够大幅提高数据查找速度;叶子节点无序且存储在PM内,在该设计下每次数据插入仅需要一次持久化操作,能够大幅减少写入开销.然而,系统崩溃后,内部节点的重构需要消耗大量时间.
2) FP-Tree[20].与NV-Tree不同的是,FP-Tree为叶子节点添加了一组元数据(指纹)用以管理无序的数据,每一个key对应一个1 B的散列值.查找操作通过优先访问元数据,提高了Cache命中率.同时,FP-Tree还采用硬件事务内存来保证内部节点的并发性.
3) DP-Tree[21].设计了一种基于DRAM+PM的,同时具有双阶段的索引架构.该设计基于真实硬件Intel Optane DC persistent memory访问粒度为256 B的特性,首先通过DRAM中的buffer tree对数据更新操作进行缓冲,同时将更新写入到位于PM的日志中.然后,当buffer tree达到一定尺寸后,合并到base tree中.值得注意的是base tree的内部节点也存在于DRAM中,且只允许合并之后进行修改.除此之外,DP-Tree还提出了一种粗粒度的锁,以保证索引结构的并发性.
4) FlatStore[22].结合新硬件特性,利用DRAM中的B+树或散列对更新请求进行缓冲,提出了一种横向steal的打包策略,将更新请求批量写入到PM内,有效解决了Cache与Intel Optane DC persistent memory访问粒度不同的问题,同时将每一个包填充至cache line对齐的尺寸,以解决Optane DC flush同一条cache line会产生额外延迟的问题.该优化策略可兼容绝大多数B+树和散列,能够显著提高KV-store吞吐量.
基于PM+DRAM的B+树能够利用DRAM低延迟与高吞吐量的特性高效完成数据的查找操作,进而一定程度上提高插入操作的性能.但DRAM易失特性会显著影响故障后数据恢复的效率.基于PM的B+树能够提供快速的故障后数据恢复,部分主要研究如下:
1) wB+树[23].wB+树在无序节点的基础上引入了排序(permutation)设计.该设计通过增加一个slot array对每个数据的索引进行排序,提高了查找速度,但会额外增加一次持久化操作.在节点容量较小时,slot array尺寸为8 B,可以进行原子更新,但当节点容量增大后,需要额外增加一个8 B的位图(bitmap),持久化操作又会额外增加.
2) FAST&FAIR[24].FAST&FAIR保证节点内数据有序,插入或删除数据均会引起平均节点内一半数据的移动,移动过程中通过先移动value再移动key的形式(删除与插入类似,但value的移动策略稍有不同)保证重复value之间的key不可见,读操作通过验证是否出现重复value来识别该key是否有效.同时为了保证分裂操作的失败原子性,FAST&FAIR为每次读操作添加一个检测兄弟节点的操作,这样能够检测出分裂过程中是否发生过故障,同时找到正确的数据,避免了数据不一致的情况.FAST&FAIR保证了持久化操作与所修改(包含数据移动对原始数据的修改)的cache line数量相同,获得了较低的持久化操作数量.
FAST&FAIR虽然相较于前人研究能够显著减少数据的持久化操作数量,但其持久化操作所改变的数据量更大(平均移动节点内一半数据意味着PM上一半数据需要被更新),这将影响PM的使用寿命.这一情况在包含删除操作的混合负载中更为严重,会产生不必要的数据来回移动,不仅增加了介质的磨损量,同时也显著增加了操作延迟.本研究提出的单项移动B+树能够通过利用重复value完成删除操作且不移动相关数据,既降低了删除操作延迟,又能减少后续插入操作引起的数据移动距离,减少持久化操作次数,进而减少插入操作延迟.数据移动距离的减少也意味着数据更新量的减少,对介质的磨损也有一定的缓和作用.
尽管基于PM的B+树能够在故障后快速恢复,但其性能受制于PM相对较高的读写延迟与较低的吞吐量.随着非易失介质相关技术的发展,PM性能将不断提高,因此基于PM的索引结构设计将获得更加广阔的前景.本文通过分析前人研究成果,在基于PM原地更新策略的基础上,针对节点内有序的数据排布,提出了一种新的更新策略.该策略通过避免删除操作带来的左移操作以减少数据移动,同时利用删除操作留下的空位减少下一次插入操作所需的数据移动距离,进而减少数据的持久化开销.
2 基于PM的单向移动算法
基于PM的单向移动算法旨在解决插入与删除混合操作时造成的数据来回移动过程中持久化操作开销过大的问题.该算法主要由3个操作协同完成:通过设置重复value值完成的删除操作、基于节点内数据分布且通过重复value值保证失败原子性的插入操作以及能够根据重复value值修正结果的读操作.该算法能够在降低删除开销的情况下减少后续插入操作的数据移动距离,进而减少数据持久化开销.通过易失位图实现高效的数据移动策略并提高数据访问效率.
本节将对本文设计的基于PM的单向移动算法进行详细描述.主要从节点内结构、查找操作、插入操作、删除操作、数据可见性与系统崩溃后恢复6个方面进行.
2.1 节点内结构
本文设计的ODS树节点内数据均有序排布,同时每个节点头部均有一个位图来表示节点内的空间利用情况.在本文的设计中,数据并不会在系统故障后被损坏,元数据可以在系统故障后被重构,因此为了尽量减少元数据持久化开销,该位图设计为易失状态.该状态意味着每次系统重启后,其数据均不可用,需要根据原始数据进行重构.位图前部为基于系统全局时钟的时间戳,每次系统重启后,该时间戳进行+1操作,以此来保证位图的有效性.重构操作在系统重启后第1次访问节点进行,因此不会给系统性能带来明显影响.位图可用于辅助统计节点内元素个数、二分查找以及计算数据移动的距离.
2.2 查找操作
每次查找一个节点之前,首先验证位图的可用性,若位图时间戳过期,则根据原始数据进行重构,通过遍历数据完成重构后同时返回查找结果;若位图可用,则根据位图对数据进行二分查找.查找过程中,若位图相应标记为0,则选择附近的数据进行比较.重复上述操作直至找到数据位置.为防止节点分裂过程中发生故障,查找操作还需要检测兄弟节点内数据.具体细节分析见3.2节.
2.3 插入操作
插入操作所引起的数据移动过程如图3所示:
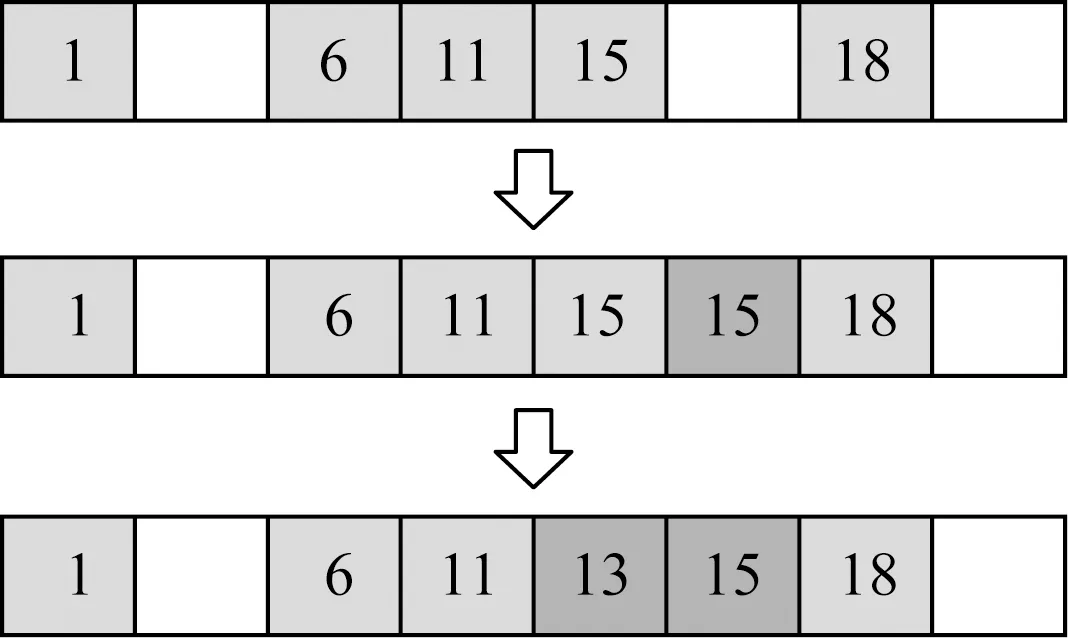
Fig. 3 Data changing after inserting 13 in the node图3 插入13后节点内数据的变化
节点初始为执行过多次原地删除之后的状态:节点内存在许多已经被删除的数据,此类数据直接由位图中的0直观表示,在原始数据中该key值两侧value相同,在位图有效期间不需修正.具体插入过程如算法1所示:
算法1.单向移动树插入算法ODS_insert(key,value).
① if 位图不合法 then
②reconstruct_node();*重构位图*
③ else
④tail=get_tail(node.bitmap);
⑤ for (i=tail-1;i≥0;i--) do
⑥ if (get_bit(node.bitmap,i)==1)
then
⑦ ifkey>node.records[i].keythen
⑧position=i+1;
⑨ break;
⑩ end if
then
records[j].value;
records[j].key;
records[position-1].value;
由于位图不做持久化处理,每个节点的位图可能存在故障后不一致的情况,因此在数据插入前应首先检测节点的位图是否可用,该过程通过比对位图内时间戳与系统时间戳是否相同,若相同,则位图可用,若不同,则位图不可用.若判断结果为位图不可用,则需要根据原始数据对位图进行重构.若位图可用,我们首先根据位图获得数据组尾部位置,然后结合位图从右向左遍历数组,通过位图内1对应的数据比对查找数据插入位置,同时记录位图内0的位置作为数组内离插入位置最近的空位位置(⑤~).~操作用来检测保证分裂过程中是否出现故障(具体见3.2节).获得数据插入位置后,根据获得的空位位置,我们采用文献[25]中的数据移动策略,将插入位置与空位之间的数据进行移动,先移动value再移动key以保证移动过程的失败原子性.在此过程中若发生断电,相同的value可以被读操作识别为当前key不可用状态,因此可保证系统崩溃后的失败原子性.由于移动过程中,load与store指令存在依赖性,因此我们不需要添加内存屏障;若数据移动到另外一条cache line内,则进行一次持久化操作.移动完成后将数据插入,再进行一次数据持久化操作,更新位图,数据插入操作完成.
2.4 删除操作
删除操作的原理是使待删除的数据对读操作不可见.在本文设计中,删除操作采用重复value值的方式使删除的数据不可见,由于value值长度为8 B,因此采用一次原子操作即可完成.重复value值的选择通常为前一组数据的value值,若被删除的是第1组数据,则value设置为兄弟节点指针(叶节点)或最左侧子节点指针(内部节点).此过程可视为我们人为地制造了一次被中断的具有失败原子性保证的数据移动操作.我们可以在逻辑上认为节点内存在很多空位,这些空位通过位图直观展示.待删除数据value值更新后,再将位图相应位置设置为0,即完成了一次删除操作.删除操作对原始数据的影响与插入操作数据移动过程中发生系统崩溃后造成的影响相同,均可以通过读操作进行修正(仅修正读操作的结果,不需要对原始数据修改).删除操作完成后若位图值为0,即节点内无有效数据,则将该节点从父节点内删除,由于本文混合负载中删除比例较低,因此不会造成显著的空间浪费.
2.5 数据的可见性
读操作存在于查找操作以及插入过程中插入位置的搜索.数据的可见性需要读操作来完成:当读操作找到相应位置后,额外读取下一个记录的value值,若2个value值相同,则当前位置的key为无效数据,读操作将继续进行直至查找到需要数据或返回未查找到.
在插入操作导致的数据移动过程中,重复value值以及之间的不可见key也会作相应移动,因此发生系统崩溃时产生的不一致仍可通过读操作验证是否有重复value来修正.
2.6 系统崩溃后的恢复
我们设计的ODS树不需要对不一致的数据进行修复,只需要在读操作过程中对不可用的位图进行重构,因此支持瞬间恢复,其原理主要为:系统崩溃后,所有节点的位图由于版本不匹配,均为不可用状态,此时读操作(包括插入操作的定位操作与查找操作)进入节点后首先判断位图是否可用,若不可用,则直接对节点内全部原始数据进行顺序读操作,若当前key对应的value值与前一个key的value值相同,则位图相应位为0,若不同则为1,遍历操作在到达第1个null时(节点内数据组的尾部)停止,此时位图修复完成,同时读操作亦相应完成.临近重复value之间的key不可见,通过位图相应位置为0表现为已删除(空闲)状态.
3 基于PM的单向移动B+树
本节详细描述了应用单向移动算法后B+树的重均衡(rebalancing)策略.主要包括选择性重均衡策略操作、节点分裂与内部整合等操作.
3.1 选择性重均衡操作
由于我们设计的算法中不使用数据修复操作,因此节点内会产生删除与系统崩溃产生的空位.尽管该空位能够通过位图有效识别,但会造成节点内疏松的结构,影响节点空间利用率.当节点无法插入新数据时,若节点内空间利用率较低,分裂操作相较于节点内部整合操作开销较大.因此我们需要通过位图分析节点内空间利用率与数据分布,选择重均衡策略.
在本文的设计中,所有重均衡策略均由插入操作触发,若数据无法被插入到节点内,则需要根据节点内空间利用率及数据分布情况选择相应的重均衡操作.目前本文采取的重均衡策略包括分裂与节点内部整合.为便于表述,我们设定2个关于重均衡策略选择的参数P1与P2.P1用于表示当前数据能否插入到当前节点内;P2为当前节点的空间利用率,用于判断应选择何种重均衡策略.具体过程如下:
找到数据插入位置后,根据位图所示数据分布判断节点内是否能够通过移动数据为待插入的数据提供空间.若能够提供空间,则P1=true;若无法提供空间则P1=false.
若P1=true,继续完成插入操作.若P1=false,根据位图获得当前P2值.若P2值小于阈值T,即节点内空间利用率小于T,则进行内部整合操作,使节点内数据紧致,若P2≥T,则进行分裂操作.实验证明节点内空缺比例为20%,设T=0.7时,能够在保证性能的同时减少树0.1%左右的空间消耗.
3.2 节点分裂
本文设计的节点分裂算法通过位图获得节点内数据的分布,并根据数据分布将部分稀疏数据紧密地写入到兄弟节点内.该算法每次分裂均包含为一次对部分稀疏数据的紧密化操作,因此能够缓解节点内数据稀疏结构对空间利用率的影响.具体算法描述如下:
算法2.单向移动树分裂算法ODS_split(node).
①shifting_position=get_shifting_data_
num(node.bitmap);
②tail=get_tail(node.bitmap);
③new_sibling=malloc(sizeof(node));
④new_sibling.sibling=node.sibling;
⑤new_sibling.bitmap=0;
⑥ for (i=shifting_position;i≤tail;i++) do
⑦ ifget_bit(node.bitmap,i)==1 then
⑧new_sibling.ODS_insert(node.records
[i].key,node.records[i].value);
⑨ end if
⑩ end for
null;
position].key,&sibling);
do
当节点需要分裂时,处理流程为:1)确定需要移动的数据(①②).2)分配一个新的节点并进行初始化(③~⑤).3)根据原节点内位图,将需要移动的数据插入到新节点中,插入过程中新节点内能够紧密地保存原节点内一半数据,新节点内位图也会被相应修改(⑥~⑩).4)修改原节点的兄弟指针指向新分配的节点().5)将原节点内分裂位置的value设置为null并持久化().6)将新节点添加到父节点中().7)修改原节点位图(~).
在分裂过程中,若故障发生在1)与4)之间,对数据的操作均不可见.若故障发生在4)与5)之间,由于4)5)在操作过程中,均可保证失败原子性,因此仅需分析4)完成后到5)开始之前的时间段内的故障情况.在此情况下,新节点对父节点不可见,同时存储的数据与原节点后半部分相同.故障后,原节点内仍为需要分裂状态,因此读操作执行时需添加一个判断操作:当key大于节点内最大key时,需要额外访问兄弟节点,通过兄弟节点内最小key与原节点内最大key作对比,若兄弟节点内最小key小于原节点内最大key,则意味着此过程中发生了故障,需要继续完成分裂操作.若兄弟节点内最小key大于原节点内最大key且小于待查找的key,则此故障发生在5)6)之间,重复上述读操作至返回结果.6)操作为原子性操作,7)操作不需要持久化,因此不需要考虑失败原子性问题.
3.3 节点内部整合
当节点需要进行内部整合时,仅需根据节点位图,计算出每个数据的位移,将所有数据左移至紧密相邻,然后更新位图即可.通过利用位图分析,可以直接对原始数据进行最短路径的移动.上述移动过程采取和右移相同的重复value移动策略,在故障发生时,虽然位图不可用,读操作可以修正移动过程中产生的不一致,即将其视为一次已经完成的删除操作.
4 实验与结果
由于本文研究针对基于单一PM架构的B+树,同时WORT源码中并未实现删除操作,因此出于严谨性考虑,本文对比实验采用wB+树与FAST& FAIR.其中wB+树采用bitmap+slot array的结构.尽管本实验室目前没有配置Intel Optane DC per-sistent memory,但本文设计的单向移动B+树旨在减少基于PM的索引结构持久化开销(持久化操作数量及其时间开销),故可使用quartz[25]进行模拟实验.
4.1 实验环境
我们实验使用的服务器环境配置如表1所示.由于quartz目前不能模拟PM写延迟,因此我们参考前人研究通过在clflush指令后添加延迟来模拟PM写延迟[4].同时由于quartz无法同时模拟PM读延迟与带宽,因此我们假定PM与DRAM带宽相同.在quartz配置文件中,我们设置模拟器为NVM only模式,其他参数采用默认配置.通过对不同索引结构在不同大小节点上性能的测试,我们采取的最优节点大小分别为:FAST&FAIR与ODS节点大小为256 B,wB+树节点大小为512 B.
Table 1 Experiment Configuration表1 实验环境配置
我们使用YCSB[26]分别生成了单一操作的工作负载及混合操作的工作负载用于测试索引结构的单一负载性能及混合负载的性能.由于我们采用重复value值作为失败原子性的保障条件,且value长度为8 B,支持原子操作,因此在定长key,value对场景下,key的长度超过8 B并不会产生失败原子性问题.为简化实验,我们故将key,value长度均设置为8 B.
4.2 单一负载测试
我们分别测试了ODS,FAST&FAIR,wB+树在不同读写延迟下的单一负载性能.首先分别使用了5万个数据进行预热,然后分别对其进行数量为5万的插入、查找与删除测试.其中由于ODS使用原地删除,因此节点内数据的结构较为疏松.在保证数据量相同的情况下,我们分别设定ODS的空缺比例为10%(ODS0.1)与20%(ODS0.2).完成插入操作后,ODS与FAST&FAIR均占用12 182个节点,ODS0.1占用12 343个节点,ODS0.2占用12 507个节点.相比FAST&FAIR,ODS的3个版本占用空间分别提高了0%,1.3%,2.7%.由此可见插入操作能够较有效地填补删除操作留下的空缺.在不考虑预热阶段持久化次数的情况下,各索引结构的操作产生的持久化操作如表2所示,在10%删除预热情况下,ODS0.1与FAST&FAIR相比,插入操作能够减少4.9%、删除操作能够减少60.6%的flush操作数量;在20%删除预热情况下,ODS0.2与FAST& FAIR相比,插入操作能够减少9.6%、删除操作能够减少60.5%的flush操作数量.
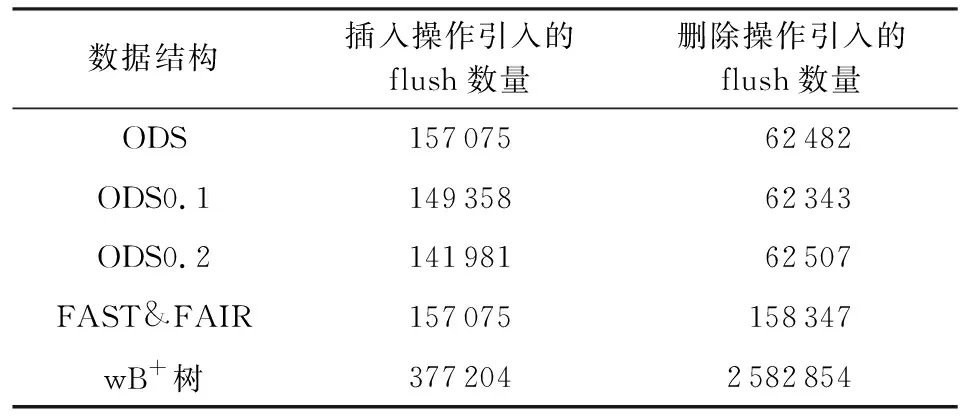
Table 2 Flush Number of Insertion and Deletion in Different Data Structures
性能评估结果如图4所示,3种版本的ODS相较于其他2种树,删除性能均大幅提高,所用时间为FAST&FAIR的32.2%~34.4%,wB+树的3.6%~4.5%.这是因为我们采取的原地删除操作能够大幅减少删除操作引起的数据移动,进而减少持久化操作,提高性能.稀疏版本ODS插入操作性能在3种延迟环境下,所用时间分别为FAST&FAIR的90%~93.5%,95.7%~97%,93.1%~96.5%;wB+树的45.9%~47.3%,42.7%~42.3%,41.7%~43%.稀疏化的ODS能够有效减少插入操作引起的数据移动距离,进而减少持久化操作数量,从而提高了插入性能.查找操作在延迟较高的情况下性能低于FAST&FAIR与wB+树.这是由于稀疏化结构导致查找的数据量增多,尽管我们使用了位图加速数据查找速度,但只是单纯减少了处理器层面的计算操作,需要处理器实际处理的cache line增多了,此时内存性能成为瓶颈,因此性能对内存延迟比较敏感.

Fig. 4 Performance of different operations under specified latency图4 不同延迟下各操作的性能
4.3 合成负载测试
在合成负载测试中,我们测试的索引结构与单一负载测试相同.预热数据量为0.5M,操作数量为0.5M.负载插入、删除与查找比例分别为3∶1∶1(W1)与1∶1∶3(W2).
在不同数据结构下,我们采用不同合成负载对索引结构进行测试,其中flush操作统计如表3所示:在插入、删除与查找比例为3∶1∶1情况下,相较于FAST& FAIR,ODS能够最多减少23%的flush次数;相较于wB+树能够减少85.5%的flush次数.在插入、删除与查找比例为1∶1∶3情况下,相较于FAST&FAIR,ODS能够最多减少34.8%的flush次数;相较于wB+树,ODS能够最多减少92.7%的flush次数.wB+树在节点分裂与合并时需要记录日志,会产生大量的持久化操作,ODS不需要记录日志同时删除操作能够减少大量持久化操作,因此相比之下能够大幅减少持久化操作数量.FAST& FAIR在插入数据时会造成节点内大量数据的移动,ODS利用删除留下的空位能够有效减少数据的实际移动距离,能进一步减少持久化操作数量,同时删除操作也能减少大量持久化操作数量.
性能结果如图5所示:图5(a)显示了60%插入、20%删除、20%查找条件下5种索引结构的性能.相较于FAST&FAIR,不同延迟下,3个版本ODS性能分别提高了14.1%,14.6%,11.7%.相较于wB+树,不同延迟下3个版本ODS性能分别提高了82.9%,74.8%,75.4%.图5(b)显示了20%插入,20%删除,60%查找条件下5种索引结构的性能.相较于FAST&FAIR,不同延迟下,3个版本ODS性能分别提高了18.1%,18.8%,22.1%.相较于wB+树,不同延迟下3个版本ODS性能分别提高了74.2%,80.3%,81.7%.
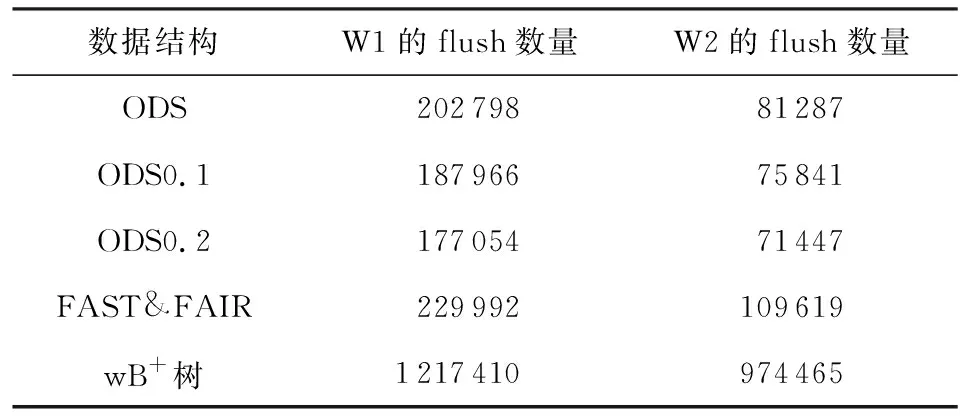
Table 3 Flush Number of Different Data StructuresUnder Different Workloads
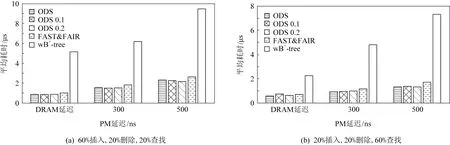
Fig. 5 Performance of index structures under different latency for different synthetic workloads图5 不同合成负载条件下各索引结构在不同PM延迟下的性能
5 总 结
持久性内存的出现为主存辅存一体的存储结构提供了强大的契机,索引结构设计将趋向于内存索引结构.然而传统内存索引结构由于内存的易失性,通常不需要考虑失败原子性问题.因此基于持久性内存的索引结构为保证其失败原子性,需要更加细致的设计.本文提出了一种基于有序节点内数据分布的数据移动策略,通过原地删除产生的节点空位,减少数据的移动距离,同时减少持久化操作的数量.结合上述移动策略,本文实现了一个单向移动B+树,通过基于节点内数据分布的分裂及整合操作,显著减轻了节点稀疏化造成的负面影响.目前本设计仅考虑单线程情况,下一步工作为设计一个多线程版本的单向移动B+树.
