面向跨数据中心网络的节点约束存储转发调度方法
2021-02-06岳胜男孙卫强胡卫生
林 霄 姬 硕 岳胜男 孙卫强 胡卫生
1(福州大学物理与信息工程学院 福州 350116)2(区域光纤通信网与新型光通信系统国家重点实验室(上海交通大学) 上海 200240)(linxiaocer@fzu.edu.cn)
随着新兴在线应用与云服务的迅猛发展,跨数据中心的大数据传输需求正呈现井喷态势[1-2].目前典型的大数据传输应用,例如数据中心(datacenter, DC)备份、大科学计算等,其传输数据量多达数百太字节(TB),传输所需带宽高达数吉比特每秒(Gbps),传输时间甚至可持续数天[3-5].这对跨数据中心网络提出了前所未有的挑战.由于大数据传输时间长(数小时到数天),因此数据往往对传输延时不敏感,具有延迟容忍性(delay tolerant).为了应对上述挑战,许多研究工作尝试利用延迟容忍性,为大数据的传输与调度提供额外灵活性[3-9].
文献[3-9]的共同特征之一是采用端到端(end-to-end, E2E)连接传输大数据.然而,网络中带宽资源的使用情况在时间和空间上均呈现不均衡性,这使得在较大网络范围内进行E2E数据传输难以实现.例如,在跨时区的数据传输中,由于不同时区中网络出现带宽使用的峰谷时间不一致,跨多个时区的E2E高带宽通路难以实现.即便在同一个时区中,由于网络中各条链路带宽可用情况差异甚大,能够提供给E2E传输的时间窗口也很小,难以满足大数据传输要求[10].为承载持续上升的网络高峰期流量,即便网络在非高峰期有大量闲置带宽,数据中心运营商仍然必须不断从互联网服务提供商(Internet service provider, ISP)购买更多的带宽,或者持续升级其专用线路的带宽容量.
为了克服E2E传输面临的困境,DC存储被引入数据传输路径.当网络流量进入高峰时段(例如正午),将延迟容忍的数据缓存于途经节点(例如DC),从而避免大、小数据流的带宽竞争;当网络流量进入低谷时段(例如凌晨),充分利用大量闲置带宽资源继续传输数据,即通过存储转发(store-and-forward, SnF)“错峰传输”大数据,已被证明能有效解决跨数据中心间大数据传输难题[11].
本文以海量DC存储与光电路交换(optical circuit switching, OCS)的结合作为研究场景.一方面,OCS可以为大数据提供高带宽、大容量、低开销的传输通道.另一方面,通过SnF实现数据分段传输,避免了传统OCS面临的E2E传输困境[11-15].然而,存储的引入将传统的路由问题变为更加复杂的SnF调度问题.求解该调度问题,不仅需要在空间上寻找传输路径,还需要在时间上规划何时传输、何时缓存.相比传统路由问题,SnF调度问题求解难度大,计算复杂度高[10].此外,不恰当地调度存储、带宽资源,反而导致绕路、网络资源碎片化等问题,进而恶化网络性能[13].显然,SnF效能的发挥取决于能否高效、合理求解SnF调度问题.
本质上,SnF的灵活性取决于数据传输路径上的存储节点数.每个存储节点都为调度决策提供一个SnF选项.存储节点越多,SnF调度方案就越灵活.目前大多数研究工作旨在最大限度地发挥SnF的灵活性,因此将数据传输路径上的所有节点均纳入SnF调度决策[10-21].当每个节点接收到数据后,其必须决定是否存储该数据、需要存储多长时间,以及应该以何种速率将该数据传输到下一节点.这导致调度问题的复杂度随传输路径跳数的增加呈指数增长[10,15].因此,在大规模网络、动态网络场景下,调度问题将变得难以求解.
在实际传输过程中,数据通常只需在部分途经节点,而非途经的所有节点,进行SnF即可满足传输需求[13,16].例如,文献[16]研究表明大多数请求通过1,2次SnF即可到达目的地.此外,在OCS网络中,每次SnF都需要进行昂贵的光电光(optical-to-electrical-to-optical, OEO)转换,这会带来额外的功耗和网络管控开销[11].由此,本文将探索如何将部分途经节点而非所有节点纳入SnF调度决策,从而降低计算复杂度的方法.
本文的主要贡献有3个方面:
1) 首先借助理论分析模型,比较了SnF与2种典型E2E传输方式的调度性能与复杂度.研究表明,在某些情况下,即使使用单个存储节点传输方式,也可以获得与多存储节点传输方式近似的调度性能.
2) 进一步扩展理论分析模型,量化分析了参与调度决策的存储节点数量对SnF调度性能与复杂度的影响.研究表明,在调度过程中,仅将部分途经节点纳入调度问题决策,同时扩大时间维度的调度范围,不仅能获得更好调度性能,同时能有效降低计算复杂度.
3) 提出了节点约束SnF调度方法.该方法将部分数据途经节点纳入调度决策,同时根据所选节点进行拓扑抽象.给定相同的计算复杂度限制,该方法可以对更大时间范围内的网络状态进行搜索,比使用所有节点进行调度的现有调度方法作出更优的调度决策.仿真表明,该方法在阻塞率和运算时间方面优于现有调度方法.
1 相关工作
1.1 现有SnF调度方法
本文根据调度策略,将现有SnF调度方法分为2类:1)基于最大灵活性(max flexibility, MF)策略的调度方法,该策略旨在最大化SnF的调度灵活性,因此其将所有网络节点都纳入调度决策;2)基于节点约束(node constraint, NC)策略的调度方法,该策略旨在以牺牲一定的调度灵活性为代价简化调度问题,因此其仅将部分网络节点纳入调度决策.图1对现有SnF调度方法进行分类总结.

Fig. 1 Classification of existing SnF scheduling methods图1 已有SnF调度方法及其分类
1) 基于MF策略的SnF调度方法
多数学者旨在充分利用现有网络基础架构,最大程度地发挥SnF调度的灵活性,即采用基于MF的调度策略.这些学者针对所有网络节点均部署有存储的网络场景开展研究,即完全部署(full place-ment)网络场景[10-23].
在此基础之上,学者们提出的SnF调度方法会将数据传输路径上的所有节点均纳入调度决策[10-23].因此,每个节点都为SnF提供了潜在可能.在这些研究工作中,SnF调度问题被建模为优化问题,例如线性规划问题和网络流量问题[10-13,18-21],并且采用经典的优化算法或启发式算法来求解问题,实现路由、调度与资源分配的最优解.现有以优化建模为基础的SnF调度方法复杂度较高,更适合解决小规模网络、静态网络场景下的离线调度优化问题.静态网络场景中,请求的数量和到达时间都是提前已知的.然而,文献[14]的研究表明,SnF调度问题的规模会随着传输路径跳数的增加而呈指数增长.这意味着当调度问题规模较大时,问题可能难以求解.因此,上述SnF调度方法难以为大规模网络、动态网络场景提供实时调度.在动态网络场景中,请求是随机到达网络,请求的数量和到达时间都是随机的.一部分学者同样也针对完全部署网络场景开展研究.但是,他们对调度过程进行了部分限制[22-23].文献[22]旨在通过最少的SnF次数来完成数据传输.因此,文献[22]所提出的调度方法是采用贪婪算法,从允许一次SnF开始逐次递增SnF次数,直到找到可行的SnF方案为止.文献[23]旨在减轻存储系统的高速读写负担,所以仅允许源节点缓存数据.然而,文献[22-23]均未研究存储节点数对SnF的性能与复杂度的影响.
2) 基于NC策略的SnF调度方法
采用基于NC的调度策略以牺牲一定的调度灵活性为代价,简化调度问题.其中,一部分学者针对完全部署网络场景开展研究[24-25];另一部分学者针对仅部分网络节点部署有存储的网络场景展开研究,即部分部署(partial placement)的网络场景[26-28].
在完全部署网络场景下,文献[24-25]比较了SnF和提前预约机制(advance reservation, AR).AR可等价于仅有源节点具备存储功能的一个SnF特例.文献[24-25]研究表明,当网络负载较高时,与SnF相比,AR所能带来的性能增益是有限的.
在部分部署网络场景下[27],文献[26]针对3节点串联网络展开研究,其中仅有中继节点具备SnF能力.文献[26]将SnF调度问题建模为单跳、单路径传输问题,但并未考虑任何路由或调度问题.在文献[27]中,当E2E光路无法建立时,调度方法将尝试从源节点建立光路到最近的存储节点,以便缓存数据,等待一段时间后再尝试建立从存储节点到目的地的光路.尽管数据传输路径可能会途经多个中继节点,但是只有一个中继节点是存储节点.这就极大限制了SnF的灵活性,以及所能带来的性能增益.此外,文献[27]将存储部署问题转化为设施选址问题(facility location problem),并通过拓扑中心性求解该问题.显然,存储部署主要取决于网络拓扑特征,但并未考虑任何调度复杂度问题.文献[28]旨在以最小的存储使用量获得最大网络数据传输能力.文献[28]将路由问题与存储使用问题转化为最大流问题(maximum flow problem),从而实现对上述2个问题的联合优化.文献[28]同样也没有考虑存储节点数量对于调度复杂度的影响.
3) 现有研究工作的总结
多数工作主要研究基于MF策略的SnF调度方法.这些工作所提出的调度方法更适合小规模网络、静态网络场景下的离线调度优化,难以为大规模网络、动态网络场景提供实时调度.另一部分工作研究如何使用源节点或部分中继节点进行调度,即采用基于NC策略的SnF调度方法.然而,这些研究工作旨在于减少存储部署或使用量,并未考虑存储节点数量对于调度性能和复杂度的影响.显然,调度方法的设计本质上是对性能与复杂度的折中.设计高效的SnF调度方法应当仔细考虑用于调度决策的存储节点数.然而,现有的研究工作尚未充分考虑该问题.
与现有基于MF策略的调度方法不同,本文所提出的新型调度方法将NC调度策略融入基于时移多层图(time-shifted multilayer graph, TS-MLG)[16]的路由调度,有效减少了调度决策过程需要的存储节点数量.在此基础之上,新型调度方法使用基于存储节点的拓扑抽象,在保证调度性能的同时减小调度问题规模、降低调度问题求解难度.现有基于NC策略的调度方法通常固定选择源节点或部分中继节点作为存储节点.与此不同,新型调度方法根据节点对之间路由跳数的不同,选择合适的存储节点数,获得了低复杂度、高调度性能,更适合为大规模网络、动态网络场景提供实时、高效的调度服务.
1.2 时移多层图
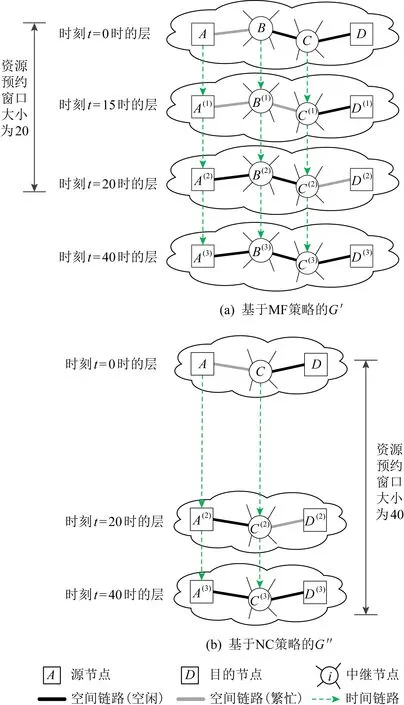
时移多层图[16]是一种面向SnF的路由调度框架,是由多个层组成的图,如图2所示.TS-MLG中每层都是网络拓扑在某个时刻的快照,反映了当时的网络状态.TS-MLG通过一系列拓扑快照,捕捉了随时间变化的网络状态.例如,TS-MLG的最顶层表明时刻t0链路E—F没有可用带宽.第2层表明时刻t1链路E(1)—F(1)有可用带宽.此外,TS-MLG引入时间链路(temporal link)和空间链路(spatial link)的概念.请求穿越时间、空间链路分别表示数据缓存和数据传输.仅需对TS-MLG进行最短路由,即可获得一条“穿越时空的端到端”路径,同时实现空间路由与时间调度的融合调度、带宽与存储资源的联合分配,极大简化了SnF调度问题的求解过程.
假设传输请求r在时刻t0到达网络,要求从节点A向节点E传输数据.然而,在时刻t0无法进行E2E传输.但通过对图2所示的TS-MLG进行路由搜索(例如使用Dijkstra算法),即可找到路径A—F—F(1)—E(1),其中节点F是中继存储节点.显然,借助TS-MLG,时空二维的SnF调度问题被转变为一维的路由问题.

Fig. 2 Time-shifted multilayer graph (TS-MLG)图2 时移多层图(TS-MLG)
随着请求的到达和离开,网络状态将发生改变,TS-MLG的层数也将发生动态改变.当网络产生新状态,新层将被添加到TS-MLG.随着时间流逝,当现有网络状态超时,相应的层将被从TS-MLG中移除.
路由算法的计算复杂度通常取决于网络拓扑的规模.TS-MLG的规模等于网络拓扑节点数乘以TS-MLG的层数.因此,TS-MLG的层数很大程度上决定了对其进行路由搜索的计算复杂度.由于数据流的突发性可能会导致TS-MLG的层数出现短时激增,使得后续请求的路由复杂度陡然增大.为了限制复杂度,用于路由的层数必须予以限制.因此,请求是否能被网络接收取决于请求是否能在给定的TS-MLG层数内找到有效路径.
2 不同数据传输方式的比较研究
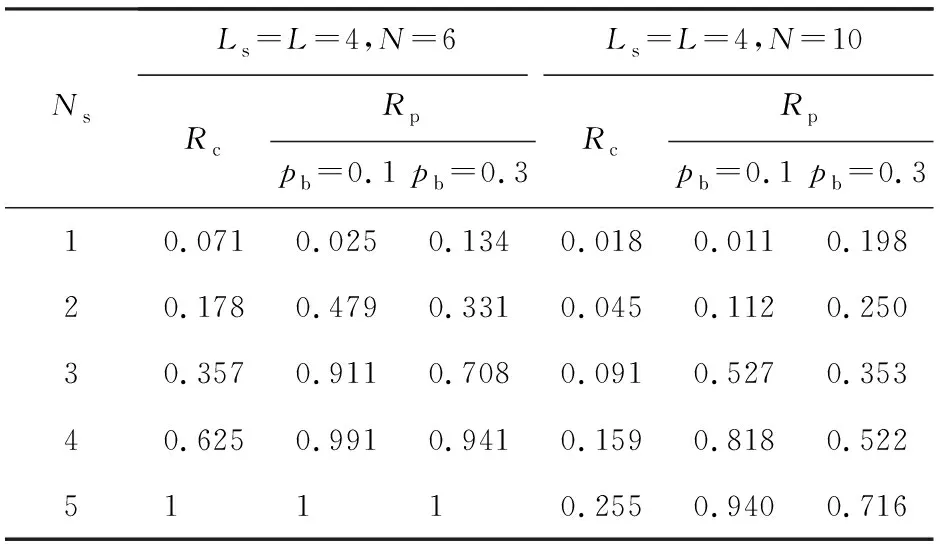
立即预约(immediate reservation, IR)和提前预约(advance reservation, AR)是OCS网络中2种典型E2E数据传输方式[29].本节首先简要介绍了IR,AR,SnF的基本原理,随后利用理论模型比较分析了3种数据传输方式的性能与复杂度.本文所涉及的主要符号及其含义如表1所示:

Table 1 Table of Notations
在IR中,请求是否能被接收取决于当前网络带宽是否能够提供E2E传输.当请求到达网络时,网络调度器(scheduler)必须立即根据网络当前的带宽资源可用情况作出调度决策.在AR中,请求的传输可以被推迟,并等待可用的E2E连接出现再开始传输.源节点具备推迟请求传输的能力.因此,当请求到达网络时,网络调度器根据网络当前与未来的带宽资源可用情况作出调度决策.在SnF中,每个节点都可以进行SnF.因此,当请求到达网络时,网络调度器根据网络当前与未来的带宽与存储资源可用情况作出调度决策.IR与AR可等价为SnF在没有任何节点或仅有源节点具备存储能力时的2种特例.
2.1 建模分析
本文扩展了文献[14]的分析模型,比较IR,AR,SnF.假设固定路由R={s,i1,i2,…,iN-2,d},其中s是源节点,d是目的节点,N表示固定路由的节点总数,且N≥2.基于TS-MLG的IR,AR,SnF路由模型,如图3所示.假定L层可以用于调度.

Fig. 3 Routing models of the three transfer manners图3 3种传输方式的路由模型
IR的TS-MLG仅由一层组成,如图3(a)所示.这是因为IR中仅考虑了当前网络状态.在图3(b)中,AR的TS-MLG由L层组成,因为AR需要同时考虑当前和未来的网络状态.此外,仅源节点通过时间链路相互连接.在图3(c)中,由于每个节点都可以进行SnF,所以TS-MLG包含多层、多条时间链路.令d(l)表示TS-MLG中位于第l层的目的节点d,其中l∈[1,L].在本文中,备选路径(alternate path)定义为TS-MLG中从节点s到节点d(l)的路径,其中l∈[1,L].备选路径并未考虑每条链路的资源可用性.有效路径(viable path)定义为在每条空间或时间链路都具备所需带宽或存储资源的备选路径.
借助TS-MLG,本文将调度问题转变为路由问题.求解路由问题的简单方法之一就是列举从s到d的所有备选路径,并从中搜寻有效路径.因此,备选路径数量决定了路由问题的计算复杂度.例如,在图3(a)中,节点对(s,d)之间只有一条备选路径.而随着层数增加,备选路径可以到达不同d(l).如图3(b)(c)所示,(s,d)之间的备选路径数随层数增加而增加.P(s,d)(N,L)定义为从s到d(LL)的所有备选路径的总数,其中LL={1,2,…,l,…,L}.本文采用P(s,d)(N,L)来衡量SnF调度问题的计算复杂度.
此外,SnF的主要思想是采用存储置换带宽.因此,分析模型需要进一步考虑网络资源的可用性.预约失败率F(s,d)(N,L)定义为未能从数量为P(s,d)(N,L)的备选路径集合中找到有效路径的概率.令pb表示请求未能在一条空间链路上找到所需带宽的概率;ps表示请求未能在一条时间链路上找到所需存储的概率.本文采用F(s,d)(N,L)来衡量SnF调度问题的潜在调度性能.
(1)

(2)

N和L决定了TS-MLG的规模.增加N表示选择一条更长的路由传输数据,而增加L表示扩展时间维度的调度范围(例如允许更长的数据缓存时间).
2.2 调度性能与复杂度分析
本文借助P(s,d)(N,L)和F(s,d)(N,L)对3种传输方式的复杂度和调度性能进行了比较研究.
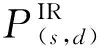

Table 2 Complexity Comparison Based on P(s,d)(N,L)
给定N,L,pbps,图4比较了3种传输方式的预约失败率,即F(s,d)(N,L).图4(a)~(c)假设ps≪pb.因为在典型的跨数据中心网络中带宽资源较为稀缺,而存储资源较为丰富.在某些城域网应用场景中,例如传统通信机房DC化(center office re-architected as datacenter, CORD)和面向边缘计算的微型DC,有限的存储资源可能不足以满足大数据传输需求.因此,在这些网络场景中,pb和ps的取值值得未来继续研究.

之前的研究均考虑ps≪pb的情况.为了不失一般性,本节进一步考虑ps≫pb的情况.图4(d)假设pbps=0.010.3.此时,带宽资源充足,但是存储资源稀缺.此时,增大L难以有效降低与

Fig. 4 Performance comparison based on F(s,d)(N,L)图4 基于F(s,d)(N,L)的调度性能比较
2.3 分析与总结
借助复杂度与调度性能分析模型,本节比较了IR,AR,SnF这3种数据传输方式,主要发现如下:
1) 虽然IR和AR的复杂度较低,但对于大规模网络、动态场景,其性能可能不足.SnF的性能优于IR和AR,但代价是复杂度较高.
2) 当N,L,pb较小时,AR和SnF之间的性能差距较小.这表明,在这种情况下,使用1个存储节点参与调度即可获得较好性能,而无需多个存储节点参与调度.但随着L的增大,AR和SnF的性能差距急剧扩大.这表明,当允许调度器在更大的时间范围内进行资源调度时,SnF比AR更有优势.
3) 相比IR和AR,SnF具备的高性能与高复杂度源于其能够使用更多的存储节点参与调度决策.因此,有必要进一步研究存储节点数对SnF的影响.
3 存储节点数量对SnF的影响
本节首先扩展分析模型以量化存储节点数对SnF的影响;然后将MF调度策略与NC调度策略进行比较研究.
3.1 建模分析

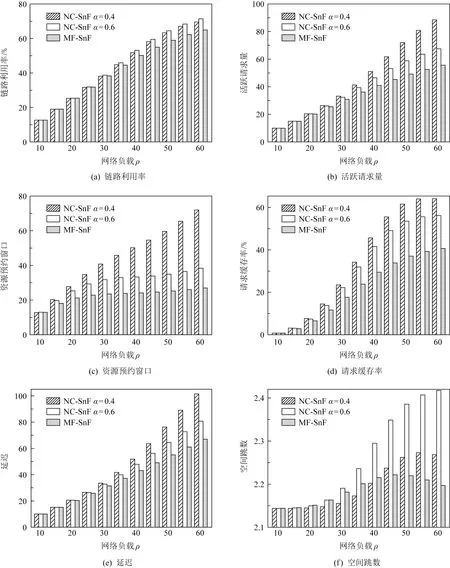
Fig. 5 SnF model based on NC scheduling strategy (Ns storage nodes and Ls layers, 1 假设固定路由R={s,i1,i2,…,iN-2,d}.令Ns表示R上的存储节点数.目的节点不能用于数据缓存.基于NC调度策略的SnF模型,简称NC模型,如图5所示,其中R上的前Ns个节点是存储节点,Ls层可以用于调度.基于MF调度策略的SnF模型,简称MF模型,如图3(c)所示.L和Ls分别表示MF模型和NC模型的层数. 当Ns=1且源节点是存储节点时,NC模型等价于图3(b)中所示的AR模型.当Ns=N-1时,NC模型等价于MF模型,如图3(c)所示.当1 图6 备选路径数和预约失败率 (3) 给定目的节点d(l),从s到d(l)的所有备选路径都具有相同的空间跳数(即N-1)和时间跳数(即l-1),并且与具体存储节点部署方案无关.由于每条时空链路的pb和ps设为相互独立,因此这些备选路径也具有相同的预约失败率,且与存储节点部署方案无关. (4) 详细证明参见附录A. 表3表明,Rp和Rc均随Ns增加而增加.随着pb减小,Rp的增幅更加明显.这表明,获得指定性能所需的Ns值随着pb的减小而减小.例如,当pb=0.3时,至少需要4个存储节点(Ns=4)才能实现Rp>0.9.但是,当pb减小到0.1时,只需要3个存储节点(Ns=3)就能实现Rp>0.9.同时,当Ns从4降低到3时,Rc从0.625降低到0.357.与MF模型相比,当pb=0.1时,NC模型仅需要35.7%的原始复杂度,即可获得超过90%的原始性能.这意味着仅将部分存储节点纳入调度,不仅可以获得理想的性能,而且能有效减轻调度过程的计算负担.当N=10时所得结果与当N=6时所得结果的变化趋势相似. Table 3 Rc and Rp when Ls=L and ps=0.01 尽管Rp和Rc均随Ns增加,但Rp和Rc之间存在间距,该间距随Ns而变化.因此存储节点的最佳数量应当使得Rp最大化而Rc最小化.但是,由于1≤Ns≤N-1,所以该间距变化始终受限.本节继续探索如何进一步扩大该间距,突破上述限制的方法. 继续研究Ls>L的情况,假设N=10,L=4,ps=0.01.本节将研究Ls变化如何影响Rp和Rc,结果如表4所示.给定Ls=L=4,当Ns从2增大到4时,Rc从0.045增加到0.159.同时,当pb=0.1时,Rp从0.112增加到0.818;而当pb=0.3时,Rp从0.250增加到0.522,如表4第1行所示.可见,当pb=0.1时,增加Ns可以将Rp增加到0.818,但代价是Rc=0.159.相比之下,给定L=4且Ns保持2,当Ls从4增大到7时,Rc从0.045增加到0.127;同时,当pb=0.1时,Rp从0.112增加到29.117;而当pb=0.3时,Rp从0.25增加到0.488,如表4第4列所示.显然,与增大Ns相比,增大Ls不仅可以提高Rp,还能保持较低的Rc. Table 4 Rc and Rp when Ls≥L and ps=0.01 借助分析模型,本节研究了存储节点数量对于SnF调度性能与复杂度的影响,主要发现如下: 1) 在时间维度的调度范围不变的前提下(即Ls=L),仅将传输路径途经的部分节点而非所有节点纳入调度决策,虽然可以减轻调度过程的计算负担,但是调度性能也会随之降低. 2) 当ps≪pb时,扩展时间维度的调度范围比使用更多存储节点参与调度更有助于提高调度性能.但是,扩展时间调度范围将导致请求经历更长延迟. 3) 当Ns 4) 设计高效的SnF调度方法应当联合优化Ns和Ls,以到达性能与复杂度的最佳折中. 本文以波分复用(wavelength-division multi-plexing, WDM)网络为基础架构的跨数据中心网络作为研究场景.借助基于软件定义网络(software-defined networking, SDN)的传输感知优化技术[30],网络运营商可以将光网络基础设施与DC资源有效整合,以实现跨DC的大数据传输.光纤中的带宽资源按照波长通道分配.每个DC的光交换平台均具备OEO转换和波长转换能力.DC可以将大数据缓存于存储集群.存储集群具备绕行企业级防火墙的能力,从而为大数据传输提供高速通道[31-32].如图7所示,当WDM2较为繁忙时,E2E传输难以保障.来自DC1的大数据通过WDM1传输并存储于DC2的存储群集.当WDM2较为空闲时,大数据通过WDM2传输到DC3.假设每个请求占用一个波长进行数据传输.与传输延迟相比,数据传播延迟、网络处理开销(例如光网络重构所需的时间)可以忽略不计[5,33].假设存储集群的数据读写速度等于单波长的传输容量.文献[34]指出大数据适宜使用专门OCS资源提供传输服务,所以本文假设部分网络资源专用于承载大数据流量. Fig. 7 SnF scheme for inter-DCNs图7 面向跨数据中心网络的SnF传输方案 受第3节的研究启发,本文将NC调度策略与拓扑抽象融入基于TS-MLG的路由调度,从而实现Ns NC-SnF方法的主要思想源于2方面.首先,在请求到达网络时,NC-SnF方法仅将部分传输路径途经节点纳入调度决策.其次,根据所涉节点,NC-SnF方法通过将TS-MLG中连接这些节点的空间链路合并,并对具有相同网络状态的层压缩,从而实现拓扑抽象.一方面,NC-SnF方法缩小了TS-MLG规模,从而减轻了调度过程的计算负担;另一方面,当可用于路由的层数有限时,相比没有拓扑抽象的传统调度方法,NC-SnF方法可以搜索时间上距离当前时刻更远的层.换言之,给定相同计算复杂度上界,相比于传统调度方法,NC-SnF方法本质上能够为请求提供更大的时间调度范围.因此,NC-SnF方法在降低计算复杂度的同时保持良好的调度性能. NC-SnF方法分为5个步骤.每个节点对(i,j)均已预先计算K条最短路由,并将备选路由存储在集合R(i,j).假设请求r的源-目的节点对为(s,d). 步骤1. 算法1第②行从集合R(s,d)中选择一条从s到d的固定路由Rk,其中Rk∈R(s,d)且|Rk|=Nk. 步骤2. 算法1第③行根据存储节点选择方案,在Rk上选择的Ns个节点用于SnF调度.令α表示Rk上可用于调度节点数占节点总数的百分比,其中0<α≤1.Ns=[(Nk-1)×α].集合S={s,I1,I2,…,Ii,…,INs-1,d},其中Ii表示被选存储节点,Ii∈Rk且|S|=Ns+1.集合S表示Rk被存储节点划分为Ns个片段.集合S的第1个节点是s,因为已有研究表明,在多数调度过程中,源节点是首个发生SnF的节点[16,24-25].为简单起见,本文假设其他被选节点等间隔分布于Rk.网络级存储节点选择或部署方案是一个有趣但复杂的问题,值得在未来深入研究. 步骤3. 算法1第④行根据Rk将原始TS-MLG图G缩减为规模较小的图G′.具体而言,图G′仅包含Rk中的节点以及连接这些节点的链路. 步骤4. 算法1第⑤行根据集合S运行算法2对图G′进行拓扑抽象,以获得抽象压缩后的子图G″. 算法1.NC-SnF调度方法. 输入:r={s,d},图G,K,R(s,d),α; 输出:Path和Find. ① fork=1;k≤K;k++ do ② 选择一条从s到d的路由Rk,其中Rk∈R(s,d)且|Rk|=Nk; ③ 根据存储节点选择方案在Rk中选择Ns个节点,得到路径片段集合S={s,I1,I2,…,Ii,…,INs-1,d},其中|S|=Ns+1,Ii∈Rk和Ns=[(Nk-1)α]; ④ 根据Rk将图G缩减为其子图G′; ⑤ 运行算法2,根据集合S对图G′进行拓扑抽象,并获得抽象压缩后子图G″; ⑥ 在图G″上运行BFS算法,寻找有效路径Path; ⑦ if找到Paththen ⑧ returnPath和Find=True; ⑨ end if ⑩ end for 算法2的主要思想是根据集合S实现拓扑抽象.该算法主要包括3个步骤: 步骤1. 算法2第①行创建1个辅助图G″=(V″,E″),其中V″=S和E″=∅. 步骤2. 算法2第②~⑧行将图G′中每个路径片段内的空间链路状态合并为图G″中的逻辑链路.LR表示用于路由的层数.LLR表示这些层的集合,LLR={l1,l2,…,lj,…,lLR}.对于图G′中第lj层的每个路径片段{Ii,Ii+1},算法2第④~⑥行找到在{Ii,Ii+1}内具有最小剩余带宽的空间链路ei,将ei添加到逻辑链路〈Ii,Ii+1〉;同时将图G′中属于节点Ii和节点Ii+1的时间链路添加到图G″. 算法2.基于存储节点的拓扑抽象算法. 输入:图G′,LR,S; 输出:图G″. ① 创建辅助图G″=(V″,E″),其中V″=S和E″=∅; ② for 图G′中所有层LLR={l1,l2,…,lj,…,lLR} do ③ for 图G′中第lj层的每一个路径片段{Ii,Ii+1} do ④ 在图G′中第lj层中找到从节点Ii到节点Ii+1具有最小剩余带宽的空间链路ei; ⑤ 将ei添加到图G″中第lj层的逻辑链路〈Ii,Ii+1〉; ⑥ 将连接图G′中的节点Ii和节点Ii+1的时间链路添加到图G″; ⑦ end for ⑧ end for ⑨ for 图G″中的所有层LLR={l1,l2,…,lj,…,lLR} do ⑩ iflj+1==ljthen Fig. 8 Comparison of the reduced graph G′ with different Ns图8 不同Ns下简化图G′比较 本节将通过图8和图9展示NC-SnF方法是如何减小TS-MLG的规模.原始TS-MLG图G如图2所示.图G由多层组成,每层包含6个节点.假设请求r需要从节点A向节点D传输数据.路由Rk={A,B,C,D}被用于请求r的传输.首先,根据Rk将图G缩减为子图G′,如图8(a)所示.图G′由4层组成,每层包含4个节点.假设α=0.4,可得Ns=2.根据4.2节所述存储节点选择方案,选择节点A与节点C参与调度,即S={A,C,D}.因此,省略连接节点B的时间链路,如图8(b)所示. 随后,运行算法2合并节点A和节点C之间的空间链路,生成逻辑链路〈A,C〉.合并图G″由4层组成,每层包含3个节点,如图9(a)所示.图9(a)中每一层逻辑链路〈A,C〉表示在该时刻从节点A到节点C的最小剩余带宽.例如,在图8(b)中,空间链路A—B在t=0时剩余带宽为0,而空间链路B—C在t=0时剩余带宽为1.因此,在图9(a)中,逻辑链路〈A,C〉的带宽在t=0时为0. Fig. 9 The merged graph G″ vs the condensed graph G″ 图9 合并图G″和压缩图G″比较 在图9(a)中,图G′中t=0和t=15的层表示相同的网络状态,即逻辑链路〈A,C〉繁忙.这些层不仅无法提供更多有用信息,还会给搜索带来额外的计算负担,因此是冗余层.算法2将t=15的层移除,得到压缩图G″,如图9(b)所示.显然,通过运行NC-SnF方法,可以极大减小TS-MLG的规模. 为了限制计算复杂度,请求只能在给定层数(即LR)内搜索有效路径.LR的值决定了时间维度的调度搜索范围.因此,算法2合并、压缩链路与层之后,时间调度范围会相应地发生改变.为了对此展开研究,资源预约窗口定义为最顶层与第LR层(即可以用于路由的最后一层)之间的时间间隔.资源预约窗口的大小与LR、层与层之间的时间间隔均有关. Fig. 10 Comparison of the reservation windows in the graphs with different scheduling strategies (LR=3)图10 不同策略下资源预约窗口比较(LR=3) 本节比较了图8(a)所示的图G′的资源预约窗口与图9(b)所示压缩后G″的资源预约窗口.假设LR=3.图10展示了不同图的资源预约窗口.在图10(a)中,G′的资源预约窗口是最顶层和第3层之间的时间间隔,即t=0和t=20的层间距.因此,图10(a)中的窗口大小为20.在图10(b)中,G″的资源预约窗口同样也是最顶层和第3层之间的时间间隔.但是,由于t=15的层被移除,第3层不再是t=20的层,而是t=40的层.因此,图10(b)的窗口大小为40.假设请求r在t=0到达网络,需要从节点A向节点D传输数据.请求r无法在图10(a)所示的窗口内找到有效路径,因此r被阻塞.相反,在图10(b)所示的窗口内,有效路径A—A(2)—C(2)—C(3)—D(3)可用于传输请求r. 简而言之,给定相同计算复杂度限制,与传统调度方法相比,NC-SnF方法能够提供更大的资源预约窗口,因此有助于降低请求阻塞率. TS-MLG的规模决定了路由算法的计算复杂度.文献[16]给出的复杂度为O((V×LR)2),V表示网络拓扑中的节点总数.NC-SnF方法使用BFS算法对压缩后的TS-MLG图G″进行有效路径搜索.BFS算法的复杂度为O(V″+E″),V″表示图G″的总节点数,E″表示图G″的总边数.在最坏的情况下,V″=LR×Ns;而E″=(LR-1)×Ns+(Ns-1)×LR.因此,NC-SnF方法的复杂度为O(K×LR×Ns). 本节模拟动态网络环境,比较NC-SnF方法与传统的SnF调度方法[12](即MF-SnF方法). 本节采用了4.1节的主要假设,并在研究中使用美国国家科学基金会网络(National Science Foundation Network, NSFNET)拓扑.为简单起见,放宽了存储容量限制.在调度过程中不考虑存储容量制约,网络调度器仅根据请求是否能在给定层数(即LR)内找到有效路径,决定请求是否被接受.假设请求到达是独立的,并在所有节点对之中均匀分布;请求的到达服从到达率为λ的泊松分布;请求的持续时间服从服务率为μ的负指数分布.网络负载ρ=λμ.链路容量,即每条链路的波长数,用w表示.每个节点对之间3条最短备用路由,即K=3.传输路径中参与调度的节点数百分比为α.当α=1时,传输路径中的所有节点均参与调度.此时,NC-SnF方法等效于MF-SnF方法.为简单起见,假设α=0.4和α=0.6.每次仿真实验产生500 000个请求,独立重复20次并取平均值. 本节首先研究阻塞率(blocking probability)如何随ρ增大而改变.可以通过增加λ或减小μ来增大ρ.由于2种情况下所得结果相似,因此在以下仿真实验中λ=1,通过改变μ来改变ρ. 仿真结果如图11所示.当ρ从10增加到60时,阻塞率增加.在图11(a)中,给定w=4,LR=4,当ρ=10时,NC-SnF方法所得阻塞率为0,而MF-SnF方法所得阻塞率为5.05×10-6.随着ρ的增加,NC-SnF方法开始出现阻塞.α值越大,阻塞率的增幅越显著.图11(b)中结果遵循相似的趋势,但是请求阻塞出现在较大的ρ值上,这是由于图11(b)中的w比图11(a)中的w大. Fig. 11 Blocking probability under various ρ (LR=4)图11 不同网络负载ρ下的阻塞率(LR=4) 直观上,存储节点数越少,阻塞率越高.然而,图11却显示相反的结果,即存储节点数越少,NC-SnF方法获得的阻塞率反而越低.为了理解该结果,本节将研究重点放在图11(a),研究其他网络性能指标如何随ρ变化,结果如图12所示.活跃请求(active request)定义为已被网络接受但尚未完成传输的请求.请求缓存率(ratio of stored requests)定义为缓存请求数与请求总数的比率.延迟定义为从请求到达网络直到请求结束传输的时间间隔. Fig. 12 Network performance under various ρ (w=4, LR=4)图12 不同网络负载ρ下的网络性能(w=4,LR=4) 在图12(a)中,当ρ从10增加到30时,NC-SnF方法和MF-SnF方法的链路利用率相似.当ρ超过35时,α=0.6的NC-SnF方法所得链路利用率明显高于其他方法,而MF-SnF方法的链路利用率低于其他方法.相反,在图12(b)中,当ρ>30时,α=0.4的NC-SnF方法的活跃请求量最多.这表明,当网络负载为中等或更高时,采用α=0.4的NC-SnF方法,网络可以同时容纳更多请求.α值越小,网络中容纳的请求越多.这是因为α=0.4的NC-SnF方法能比其他方法提供更大的资源预约窗口,如图12(c)所示.α值越小,存储节点越少,合并的空间链路就越多.这也增加了在TS-MLG中找到冗余层的机会.给定LR值,在压缩更多冗余层的情况下,层与层的时间间距变大,NC-SnF方法也就可以在更大的时间范围内搜索可用资源.因此,α的值越小,越多请求可以通过SnF到达目的节点,所以请求缓存率也越高,如图12(d)所示.简言之,得益于拓扑抽象,请求使用NC-SnF方法比使用MF-SnF方法更容易被传输.然而,随着资源预约窗口增大,请求也将经历更长的延迟,如图12(e)所示. 随着资源预约窗口的扩大,更多的请求可以通过SnF选择更短的路由,而不是通过较长的路由绕行.图12(f)表明成功传输请求的平均空间跳数.与α=0.6相比,α=0.4的NC-SnF方法产生的请求空间跳数更短.当ρ∈[45,60]时,与NC-SnF方法相比,MF-SnF方法产生的请求空间跳数更短.这是因为MF-SnF方法的阻塞率高于NC-SnF方法.对于需要通过较长的路由绕行才能完成传输的请求,MF-SnF方法难以满足这些请求的需求.随着这类请求被阻塞,MF-SnF方法产生的平均空跳明显短于NC-SnF方法. 得益于拓扑抽象算法(即算法2),空间链路和冗余层被合并和压缩,使得NC-SnF方法能够提供更大的资源预约窗口.为了验证算法2的作用,本节比较了原始NC-SnF方法和没有拓扑抽象功能的NC-SnF方法(即简化NC-SnF方法).在简化NC-SnF方法中,算法2被禁用.因此,BFS算法直接对简化图G′而非压缩图G″进行有效路径搜索.此处,w=4,LR=4.仿真结果如图13所示: Fig. 13 The original NC-SnF method vs the NC-SnF method disabling the topology abstraction (α=0.4)图13 原始NC-SnF方法与禁用拓扑抽象功能的NC-SnF方法比较(α=0.4) 给定α=0.4,原始NC-SnF方法的阻塞率优于简化NC-SnF方法,如图13(a)所示.这是因为原始NC-SnF方法中的资源预约窗口随ρ增大而增大,而简化NC-SnF方法中的资源预约窗口几乎保持恒定,如图13(b)所示. 随后,继续对比简化NC-SnF方法与MF-SnF方法,如图13(a)所示.MF-SnF方法优于简化NC-SnF方法.这是因为一方面没有了拓扑抽象功能,简化NC-SnF方法的资源预约窗口明显小于MF-SnF方法;另一方面MF-SnF方法能够比简化NC-SnF方法使用更多存储节点,因此MF-SnF方法的调度更加灵活. 本节研究了TS-MLG的节点数和层数是如何影响NC-SnF方法的算法计算时间.本节使用链路密度为0.6的随机生成拓扑进行仿真实验.链路密度定义为网络拓扑中任意2个节点之间存在边的概率.V表示网络拓扑的节点数. 表5和表6描绘了不同调度方法对给定的TS-MLG进行一次路由搜索的平均计算时间.在表5中,LR=10.计算时间随V的增加而增加.在表6中,V=10.计算时间随着LR的增加而增加.表5和表6表明,α值越小,计算时间的增幅越小.这是因为当α值较小时,需要搜索的TS-MLG规模也相应减小. Table 5 Computation Time Under Various V (LR=10) Table 6 Computation Time Under Various LR (V=10) Fig. 14 Blocking probability in different topologies图14 不同网络拓扑下的阻塞率 本节继续研究了不同的网络拓扑中阻塞率随ρ的变化情况.选取19个节点39条链路的泛欧洲全光网(optical pan-european network, OPEN)和24个节点43条链路的美国骨干网络(US backbone network, USNET)作为研究对象.此处,w=4,LR=4.图14(a)(b)分别描述了在OPEN和USNET中不同ρ下的阻塞率.图14的结果与图11的结果类似.因此,在不同的网络拓扑中,NC-SnF方法的阻塞性能均优于MF-SnF方法.然而,图14中NC-SnF调度方法获得的阻塞率略高于图11.例如,当α=0.4和ρ=20时,在NSFNET中NC-SnF方法获得的阻塞率为1.32×10-6;而在OPEN和USNET中NC-SnF方法获得的阻塞率分别为4.04×10-6和1.07×10-4.这是因为OPEN和USNET的拓扑规模大于NSFNET.因此,OPEN和USNET中给定节点对之间的路由跳数多于NSFNET.给定相同的α,NC-SnF方法在OPEN和USNET中每条路由上选定的存储节点数多于NSFNET.根据4.3节讨论可知,借助拓扑抽象算法,选定的存储节点数越少,所获得的压缩子图规模就越小,相应的资源预约窗口也就越大.因此,相比OPEN和USNET,NSFNET中NC-SnF方法可获得更大的资源预约窗口,进而获得更低的阻塞率. 本文将SnF与IR和AR进行了对比.研究表明,选择合适数量的存储节点用于调度决策,实际上是调度性能与复杂度之间的折中问题.为此,本文提出了分析模型,揭示了存储节点数对SnF复杂度与性能的影响.研究发现,在一定条件下,NC调度策略能够在降低复杂度的同时获得比传统MF调度策略更好的调度性能. 受此启发,本文提出NC-SnF调度方法,只将传输路径上的部分节点纳入调度决策.同时,NC-SnF方法引入了基于存储节点的拓扑抽象.与传统的MF-SnF方法相比,给定相同的计算复杂度界限,NC-SnF方法可以获得更大的时间调度范围.仿真结果表明,与MF-SnF方法相比,NC-SnF方法所需的计算时间更短、获得的阻塞率更低. 尽管本论文的研究工作围绕基于OCS的跨数据中心网络开展,但是研究结果对于虚电路交换网络、带宽可管理的分组交换网络等类似网络同样具有借鉴意义.本文的理论分析模型主要针对固定路由场景,而继续将研究场景扩展到通用网络场景,探索网络级存储选择与部署方案,是未来研究方向.


3.2 调度性能和复杂度分析



3.3 分析与总结
4 节点约束存储转发调度方法
4.1 网络模型与主要假设

4.2 算法研究
4.3 算法运行示例


4.4 资源预约窗口研究
4.5 计算复杂度研究
5 结果与讨论
5.1 网络性能研究

5.2 基于存储节点的拓扑抽象算法研究

5.3 算法计算时间研究


5.4 不同网络拓扑研究

6 总 结
