永磁同步电机模型预测磁场定向控制技术
2021-02-05谢刚颜学龙孙天夫梁嘉宁
谢刚,颜学龙,孙天夫,梁嘉宁
(1.桂林电子科技大学电子工程与自动化学院,广西 桂林 541004;2.中国科学院深圳先进技术研究院,广东 深圳 518055;3.深圳电动汽车动力平台与安全技术重点实验室,广东 深圳 518055)
近年来,永磁同步电动机(permanent magnet synchronous motor,PMSM)因其高精度、高效率、高转矩、宽调速范围以及运行可靠性高等优点和出色的控制性能而被广泛应用于工业应用中[1-3]。电机驱动系统中电机控制策略的优劣直接决定了永磁同步电机控制系统整体性能的好坏。在逆变器馈电的永磁同步电机驱动系统(voltage source inverter fed,VSI-FED)中[4-6],逆变器上、下桥臂开关频率的增加,提高了输出波形的质量,但是同时显著地增加了功率损耗。低开关频率降低了开关损耗的同时也减低了控制器带宽,并导致大转矩和电流波动[7-8]。目前,永磁同步电机电流控制主要方式包括:磁场定向控制、比例积分控制、滞环电流控制和预测电流控制[9-10]。磁场定向控制通过坐标变换将电机定子电流转换为转矩和励磁分量,具有控制精度高、动态性能好等优点。但是由于采用了PI电流控制器,从而导致了超调、交直轴电流耦合、无法实现任意预测步长控制等不足[11-12]。由于永磁同步电机在运行过程中参数会发生变化,而预测电流控制根据电流方程直接计算出未来时刻的电流值,未考虑电机系统当前状态的状态变量,从而是一种开环控制方式。随着集成电路微处理器的发展,数字信号处理器的发展使得模型预测控制策略在电机领域的应用成为现实,模型预测控制算法(model predictive control,MPC)由于其响应速度快及考虑了系统的非线性约束等独特的优势[13-15],近年来,被广泛地应用在电机控制系统当中。
在文献[16]中,为了在系统干扰的条件下实现性能提升,提出了一种基于龙贝格观测器的电流预测控制方法,该方法更多地关注转换器的不确定性而不是模型参数,从而忽略了电机参数变化在系统中的影响。为了实现低计算成本和降低开关损耗,文献[17]所提出的成本函数中包含了附加参数(除了状态控制变量),这增加了数字实验原型的复杂性和控制循环周期。文献[18]考虑了慢速和快速采样模型之间的耦合,提出了一种基于虚拟时刻的线性估计方法,并且基于级联结构设计了线性估计方法的数据流,从而达到了更好的动态性能。由于需要大量的计算而影响了系统的整体处理速度,为了解决大计算量在工业应用中的影响,文献[19]提出一种基于球形编码算法的多步长有限集模型预测控制策略(finite set model predictive control,FS-MPC),然而该方法仍然存在着计算量大、控制复杂等问题,增加了系统的计算负担与成本。但是,通过FS-MPC电机控制策略所合成的电压矢量us是离散的。可能会直接导致明显的转矩波动。除此之外,文献[20]通过计算3个电压矢量在下一个时刻的作用时间,然后通过第1基本有效电压矢量、第2基本有效电压矢量以及零电压矢量来合成电压矢量us。然而该方法由于需要在1个采样周期内计算出电机下一个时刻的逆变器开关状态,因此不能实现多步长预测,降低了电机重要参数的控制精度。
传统FOC控制策略由于基于PI控制器进行设计,存在着动态响应速度较低、积分器饱和、系统约束不易处理以及存在快速响应与超调和过冲之间的矛盾等问题,严重影响了现有电机控制技术的性能。针对现有电机控制技术的不足,提出的MP-FOC控制技术解决了上述传统电机控制技术所面临的问题,具有无超调、电流响应速度快等优点,并避免了交、直轴电流耦合的问题。同时由于电机参数会随运行工况改变,现有基于PI控制器的电机控制技术存在PI控制器参数整定困难的问题,而本文所提出的MP-FOC控制技术通过调节预测时间步长实现对电机转矩响应带宽的调节,只有一个需要调节的参数,即预测时间步长。因此,所提MP-FOC较MPC而言,具有多步长的预测能力,增加了电机驱动系统的控制精度。
1 PMSM数学模型及FS-MPC控制原理
基于同步旋转坐标系下,表贴式永磁同步电机(surface-mount permanent magnet synchronous motor,SPMSM)的d,q轴数学模型可以表示为
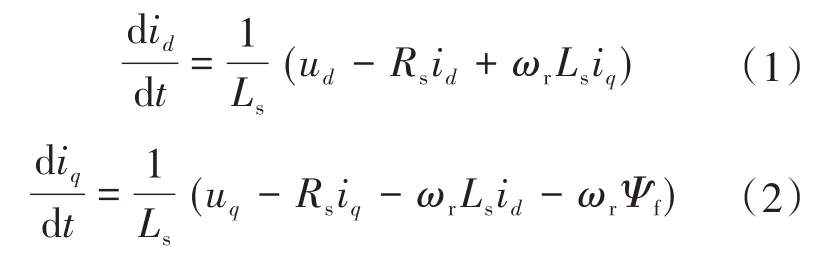
式中:id,iq分别为d,q轴电流分量;ud,uq分别为d,q轴电压分量;Rs,Ls分别为表贴式永磁同步电机的定子电阻和电感;ωr,Ψf分别为转子电角速度和电机永磁体磁链。
因为本文采用是表贴式永磁同步电机,故Ld=Lq=Ls。对式(1)、式(2)的连续时间下的数学模型利用前向欧拉离散法进行离散后的电流预测公式如下:
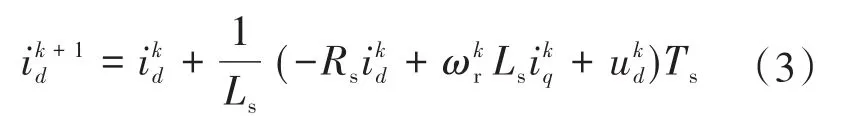

式中:Ts为离散控制周期。
两级三相逆变器上桥臂的开关状态(Sa,Sb,Sc)与ud,uq的数学关系模型可以表示为

其中
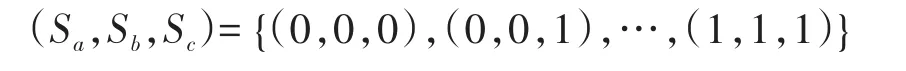
式中:(Sa,Sb,Sc)为逆变器上桥臂的8个开关状态组合;θr(k)为电机的转子位置。
2 MP-FOC控制策略
2.1 多步长预测实现
在多步长预测控制中,由于考虑了未来多个时刻的电机状态变量的预测值,从而降低了永磁同步电机驱动系统当中逆变器开关状态(Sa,Sb,Sc)的开关频率。通过多步长模型预测控制可以实现电机驱动系统重要控制参数未来时刻的整体约束。多步长预测所对应的的预测示意图如图1所示。
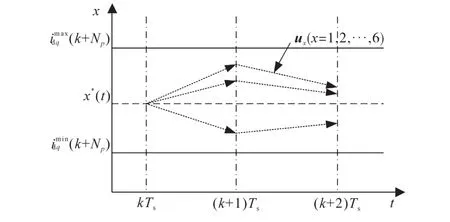
图1 多步长预测示意图Fig.1 Diagram of multi-step prediction
图1中显示了每一个控制电压矢量所对应的电机状态量的预测轨迹。在多步长预测条件下,通过选择使得下式取得最小值所对应的最优电压控制矢量,即逆变器开关状态(Sa,Sb,Sc)来进行电机控制,从而达到电机更高精度的控制要求。
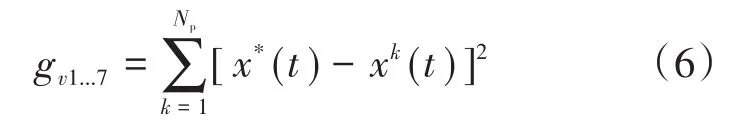
式中:x*(t),xk(t)分别为电机状态变量的参考值以及预测值;Np为预测步长;gv1...7为在有效电压矢量及零电压矢量分别作用下所对应目标函数的值。
2.2 MP-FOC控制策略
传统的磁场定向控制(FOC)策略控制原理框图如图2所示。
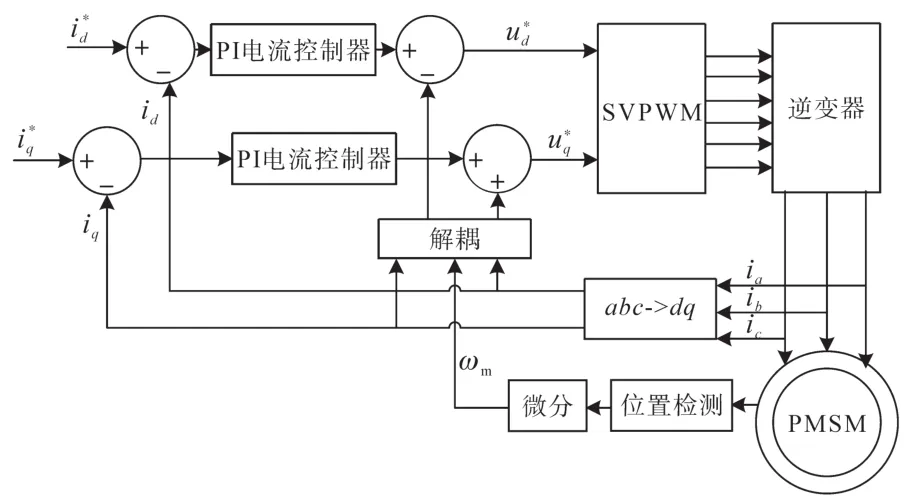
图2 FOC控制原理框图Fig.2 Block diagram of FOC
本文所提出的MP-FOC控制策略的总体原理框图如图3所示。利用图3中虚线框中的结构代替FOC中PI环,从而实现MP-FOC电流控制,达到更好的电流控制精度。
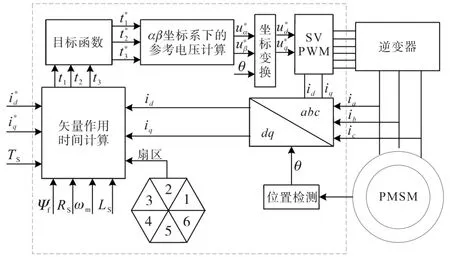
图3 MP-FOC控制系统框图Fig.3 Block diagram of MP-FOC
本文中所提方案MP-FOC以及传统的FOC都属于电流控制,即内环控制。MP-FOC控制算法可以分为以下4步:
第1步:通过式(3)和式(4)进行不断的迭代运算,可以得到预测步长为Np的d,q轴预测电流,为了消除稳态误差,令多步长预测电流等于d轴参考电流及q轴参考电流,则有下式:
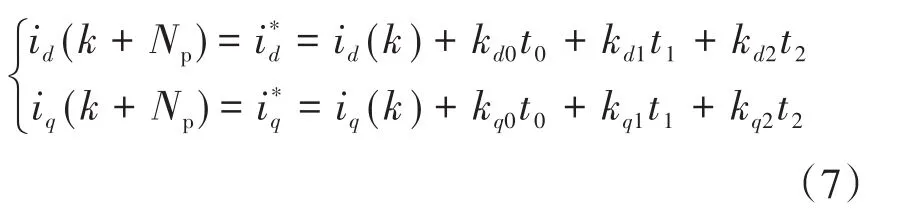
其中
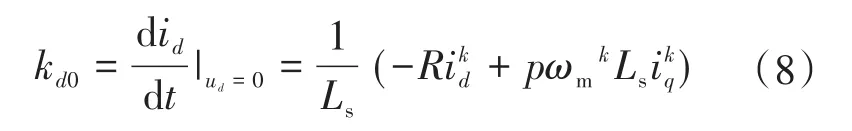
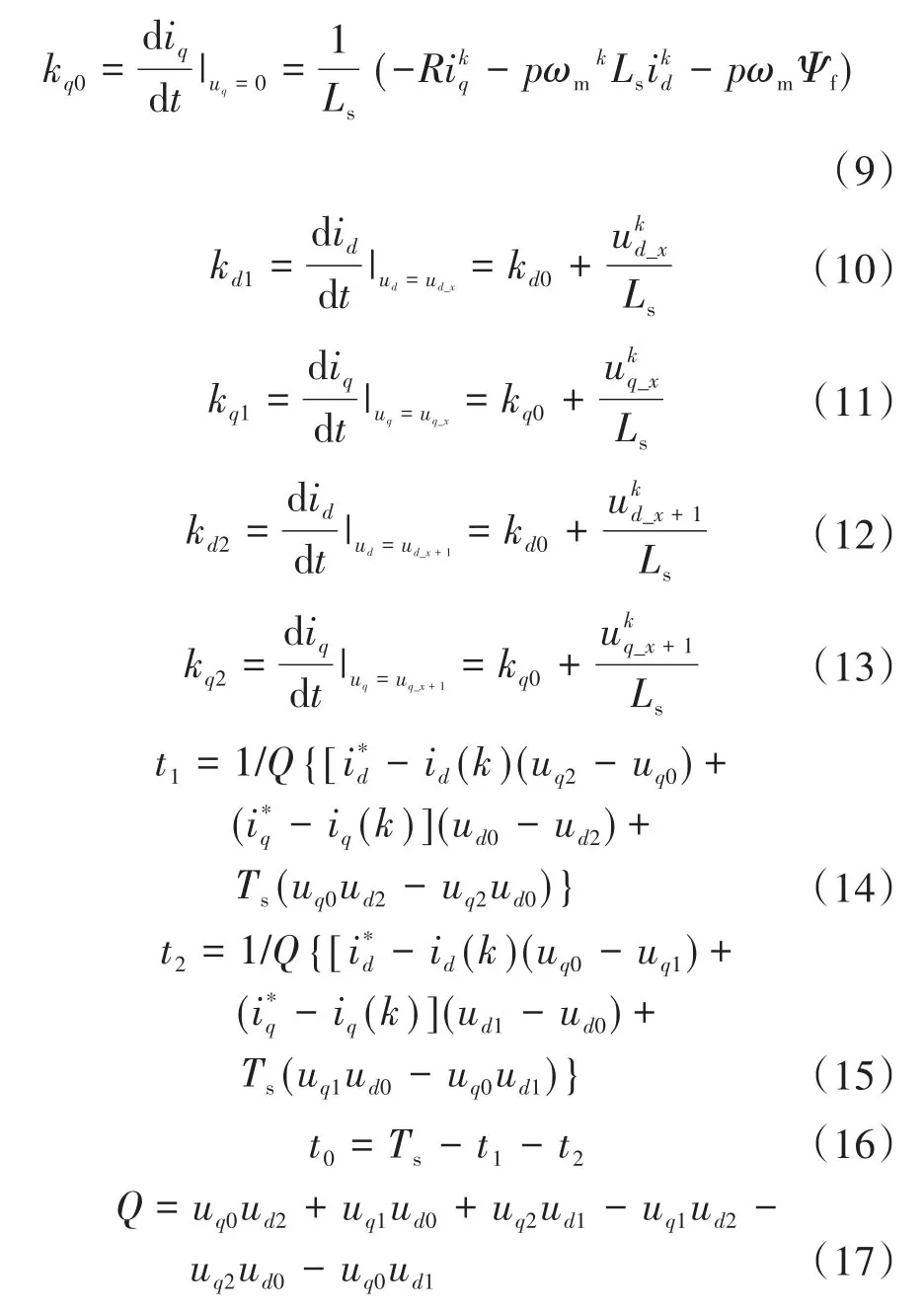
式中:p,ωm分别为电机的极对数和机械角速度;t0,Q分别为零电压矢量的作用时间以及周期内矢量作用时间系数;kd0,kq0,kd1,kq1,kd2,kq2(可由式(3)、式(4)推导得出)分别为由零电压矢量引起的d,q轴电流变化率、第1基本有效电压矢量(Ux)和相邻的第2基本有效电压矢量(Ux+1)分别引起的d,q轴电流变化率;ud-x,uq-x,ud-x+1,uq-x+1分别为第1基本有效电压矢量和相邻的第2基本有效电压矢量分别对应的d,q轴分量。
值得注意的是,为了避免永磁同步电机的输出电磁转矩、电流等重要参数出现较大的变化,因此最优控制空间电压矢量组合将在当前最优控制空间电压矢量组合所对应的扇区或者相邻的扇区中选择。如果有效电压矢量的作用时间t1,t2之和大于控制周期Ts,即t1+t2>Ts,需要利用过调制技术对周期内电压矢量作用时间进行重新分配,调制原则如下:
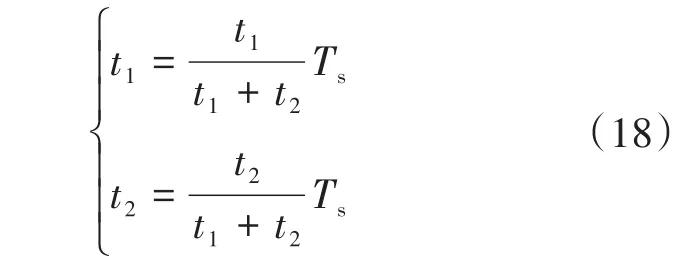
如果有效电压矢量的作用时间t1,t2不满足同时大于零的条件,则相对应的电压矢量组合将不被采用。
第2步:为了使电机产生的电流波形更加柔和,噪声少,谐波低。通过构造损失函数进行最优控制电压矢量组合选择,损失函数式如下式:

式中:N为电压矢量组合所处的扇区(扇区Ⅰ~扇区Ⅵ);Ncurrent为当前控制周期的电压矢量所在的扇区位置,即电机转子位置当前所处的扇区;C为一个远大于任何时所对应的J的值,确保当时,所对应的电压矢量组合会被舍弃。
通过选择使损失函数值最小的电压矢量组合来作用于下一电机控制周期,最佳合成电压矢量Us选择最终在电机转子当前位置所在扇区或者相邻扇区中选择。
第3步:根据目标函数选择出来的最优作用扇区N中对应的两个有效电压矢量以及作用时间来合成电压矢量Us,同时通过零电压矢量来调节合成电压矢量Us的幅度,然后计算合成电压矢量Us在α-β静止坐标系下的投影,如下式:
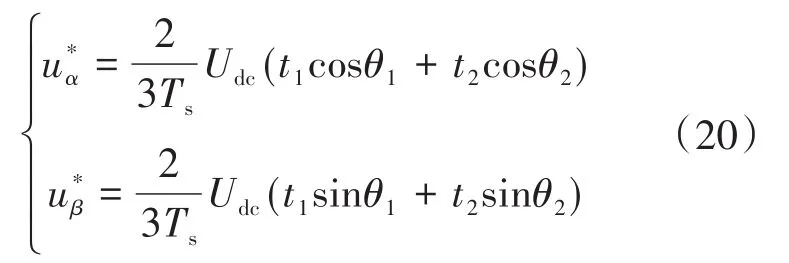
式中:θ1,θ2分别为电压矢量Ux,Ux+1与α轴的夹角。
第4步:静止坐标系变换到旋转坐标系的电机d-q轴的参考电压如下式:
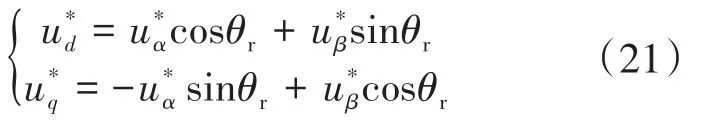
最后利用SVPWM将参考电压作用于电机,从而实现电流控制,达到电机驱动控制的目的。
3 试验结果
为了验证本文所提MP-FOC控制策略的可行性、正确性以及控制精度,同时,考虑到当预测步长大于等于4时,电机电磁转矩Te的控制精度无限接近,因此为了减少MP-FOC策略的计算量,本文设置预测步长Np=4。利用以下电机控制系统主要参数进行相应的试验验证与分析:额定转速n=3 000 r/min,额定功率750 W,额定相电流5 A,永磁体磁链0.12 Wb,定子电阻Rs=0.6Ω,极对数p=3。搭建实验平台进行相应的实验,并通过该实验平台进行FOC对比实验研究,实验平台如图4所示。实验平台由电源、转矩传感器、转速观测器、驱动板、DSPACE、电机控制器及表贴式永磁同步电机(SPMSM)等部分组成。

图4 电机驱动实验平台Fig.4 Experimental setup of PMSM
控制电机运行在不同工况下,通过分析电机在不同的工况下的定子电流Iabc以及电磁转矩Te来验证本文所提策略MP-FOC的瞬态性能、稳态性能以及控制精度。在高精度场合,由于传感器对电磁转矩采样时间较长,因此不能明显地分辨出本文所提控制策略MP-FOC以及FOC控制策略对电机电磁转矩Te的影响。电机在不同条件下运行所对应的工况说明如表1所示。
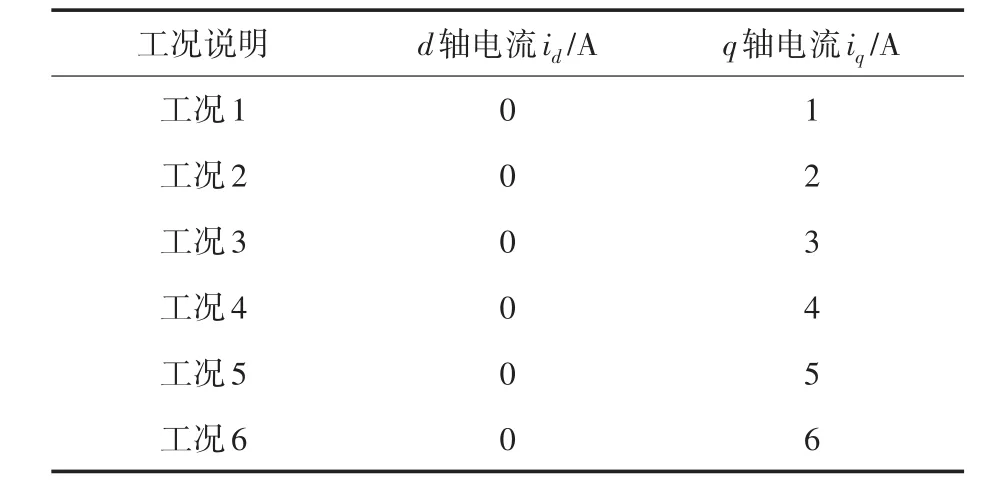
表1 电机运行工况说明Tab.1 Description of motor operating conditions
在id=0工况下,q轴电流直接决定着电磁转矩Te,因此通过分析q轴电流来分析在MP-FOC与FOC策略驱动下电机电磁转矩Te的控制精度。
当id=0时,通过控制q轴电流来改变电机的运行工况。当电机运行工况突然发生改变时,即由工况1到工况2时,施加到电机的三相电流的波形如图5所示,故本文所提MP-FOC控制策略驱动下的电机能够实现电机定子三相电流Iabc在无超调以及无过冲等前提下实现快速响应。
当电机运行在工况3时,在t1=6.2s时通过改变电机的运行工况从而使得电机运行在工况4。其瞬态响应的电磁转矩Te波形如图6所示。
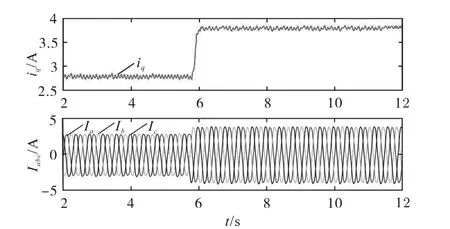
图5 定子三相电流动态响应Fig.5 Dynamic response of stator three-phase current
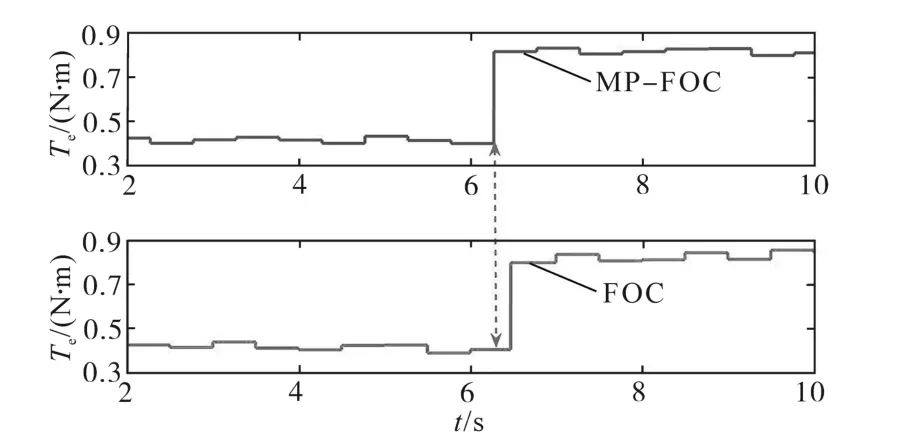
图6 电机电磁转矩Te跟随效果对比(MP-FOC与FOC)Fig.6 Comparison of motor electromagnetic torque Tefollow-up effect(MP-FOC and FOC)
从图6中可以看出,在t1=6.2s时电机运行工况突然改变时,电机在所提MP-FOC技术驱动运行下的电磁转矩Te能够马上实现快速的瞬态响应。但是电机在FOC技术驱动运行下的电磁转矩Te需要进行一定的延时后才能够实现瞬态响应。因此可以得出结论:电机在MP-FOC控制技术驱动下的电机电磁转矩Te的动态性能具有较传统FOC更好的瞬态响应能力。
图6中,由于传统FOC控制策略是通过PI环进行调节输出参考电压控制,是一种实时控制技术,无法进行硬件电路的延时补偿,因此当采用FOC控制策略进行电机控制时会存在一定的延时。由于MP-FOC控制策略具有多步长预测功能并且能够很好地实现硬件电路的延时补偿。因此,较FOC控制而言,MP-FOC能够实现较快的转矩瞬态响应。
为了验证不同工况下MP-FOC技术驱动下电机电磁转矩输出无超调、无过冲等优势,当id=0时,通过控制q轴电流来控制电机运行在工况5以及工况6之间。其电磁转矩Te的瞬态响应曲线如图7所示。
从图7可以看出,较FOC技术而言,在MPFOC控制技术驱动下的永磁同步电机转矩Te输出具有无超调、无过冲以及响应速度快等优点。
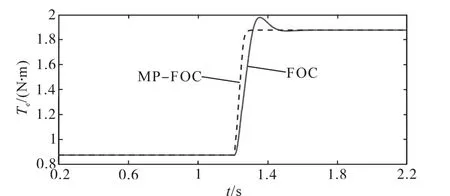
图7 电机电磁转矩Te跟随效果对比(FOC与MP-FOC)Fig.7 Comparison of motor electromagnetic torque Te follow-up effect(FOC and MP-FOC)
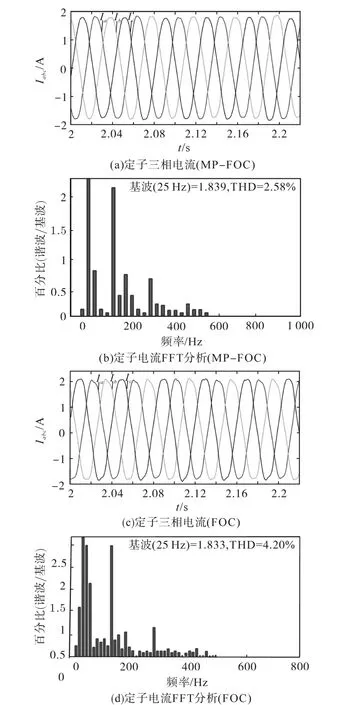
图8 定子电流波形及THD分析对比Fig.8 Comparison of stator current and THD
图8为在MP-FOC以及FOC控制策略驱动下的定子电流波形及THD分析对比图。其中,永磁同步电机运行在同种工况下,电机在MPFOC以及FOC控制策略驱动下的定子三相电流Iabc的波形如图8a和图8c所示。为了分析电机电流Iabc的谐波成分,对电机的A相电流进行FFT分析后得到图8b和图8d。从图8b可以看出,采用MP-FOC控制策略时,电流THD含量为2.58%;从图8d可以看出,采用FOC控制策略时,电流THD含量为4.20%。故本文所提控制策略相比于FOC控制策略,具有更少的电流谐波,电机定子电流具有更好的三相电流波形、谐波低、噪声少等优点。
综上所述,本文所提出的MP-FOC控制策略相对FOC控制策略而言,具有更好的稳态性能、动态响应以及控制精度,为提高VSI-FED电机系统的稳定性能以及动态响应能力提供了更好的控制策略与方案。
4 结论
围绕FOC控制策略中PI环存在着超调、动态响应速度慢、积分饱和、过冲等不足,以及传统的模型预测控制(MPC)策略无法实现多步长预测从而影响电机驱动系统的控制精度等问题,本文设计了一种基于FOC以及MPC两种控制策略的模型预测磁场定向控制策略(MPFOC)。MP-FOC利用MPC来取代FOC中的所有PI环,有效地解决了传统FOC中PI环所存在的超调、动态响应速度低以及过冲等问题。同时由于MP-FOC采用SVPWM来驱动电机,而不是逆变器开关状态,因此MP-FOC能够实现多步长预测,从而增加了永磁同步电机驱动系统的控制精度。
