格上高效的完全动态群签名方案

叶 青，赵楠楠，赵宗渠，秦攀科，闫玺玺，汤永利

（河南理工大学计算机科学与技术学院，河南焦作 454000）

0 概述

1991年，CHAUM等人首次提出群签名的概念［1］，其具有匿名性和追踪性。群签名允许群中合法成员代表群对消息进行签名，任意验证者均可利用群公钥来验证该签名的合法性，但无法确定签名者的真实身份，即匿名性；当发生争议时，群管理员可以通过追踪密钥打开签名找到真实的签名者，即追踪性。群签名的匿名性和追踪性使其被广泛应用于多种场景，如电子投票、电子商务系统和可信计算等。文献［2］指出，基于经典数论难题的传统密码方案［3-5］在多项式时间内会被量子计算机破解，基于格的新型密码体制将成为后量子密码时代的研究热点。

2010年，GORDON等人在Asiacrypt2010会议上提出格上群签名方案［6］，但该方案的密钥长度和签名长度都与群成员数量呈线性关系。2013年，LANGUILLAUMIE等人在Asiacrypt2013会议上提出一种密钥长度、签名长度与群成员数量呈对数关系的群签名方案［7］，虽然缩短了密钥长度和签名长度，但由于两者均依赖于群成员数量，因此该方案并不适用于大群组的群签名系统。2015年，NGUYEN等人提出一种简单高效的群签名方案［8］，该方案的密钥长度和签名长度与群成员数量无关，适用于大群组的群签名系统，但由于群成员私钥由群管理员产生，因此不能抵抗群管理员对群成员的陷害攻击。考虑到用户加入群的动作在任意时间都有可能发生，并且当发现某些群成员有行为不端的现象时，群管理员应有权撤销不法成员的签名权力，因此，群签名系统应包含支持群成员动态加入、撤销的加入机制和撤销机制［9-10］。然而，以上群签名方案都不支持群成员的加入和撤销。

2016年，LIBERT等人构造了一个包含加入机制的群签名方案［11］，但仍缺少群成员的动态撤销机制。2017年，LING等人基于Merkle哈希树构造了一个格基完全动态（同时包含加入和撤销机制）的群签名方案［12］，但该方案撤销成员时需要更新哈希树，计算较复杂且耗时较长，并且签名长度仍与群成员数量相关。2018年，LING等人又提出了格上本地撤销群签名方案［13］，但该方案不支持群成员的动态加入。2019年，李雪莲等人提出一种适合大群组的格基完全动态签名方案［14］，但由于在加入过程中使用变色龙哈希函数和随机采样技术，并且撤销过程中增加了与撤销图灵机的交互代价，因此该方案的开销较大。

为加快群成员的加入和撤销速度，降低完全动态群签名方案加入和撤销机制的复杂性，本文在文献［8］群签名方案的基础上，结合文献［11，14］提出的动态群签名思想，基于错误学习（Learning with Error，LWE）问题和非齐次小整数解（Inhomogeneous Small Integer Solution，ISIS）问题构造一个高效的格上完全动态群签名方案，对其进行安全性证明，并与现有的格上群签名方案进行效率对比。

1 预备知识

1.1 符号定义

本文方案中的符号定义如表1所示。

表1 符号定义Table 1 Symbols definition

1.2 格

定义1（格）设b1，b2，…，bm是n维欧式空间Rm上m个线性无关的向量，则格L被定义为b1，b2，…，bm上所有整系数线性组合所构成的集合，表示为L={a1b1+a2b2+…+ambm}(a1，a2，…，am∈Zq)，而b1，b2，…，bm称为格L的一组基。

定义3（离散高斯分布）给定实向量c∈Rm，任意实数s＞0，则格L上以c为中心、以s为参数的离散高斯分布密度函数表示为：

当s=1，c=0时，格L上任意一点x的离散高斯分布表示为：

1.3 格上困难问题

1.4 抽样函数

1.5 非交互零知识证明

2013年，LAGUILLAUMIE等人给出一个关于ISIS问题的零知识证明［7］：

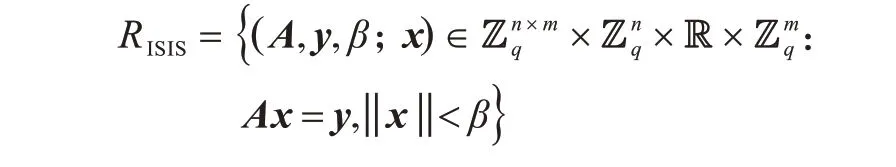
2015年，NGUYEN等人给出一个关于Split-SIS问题上的零知识证明［8］：

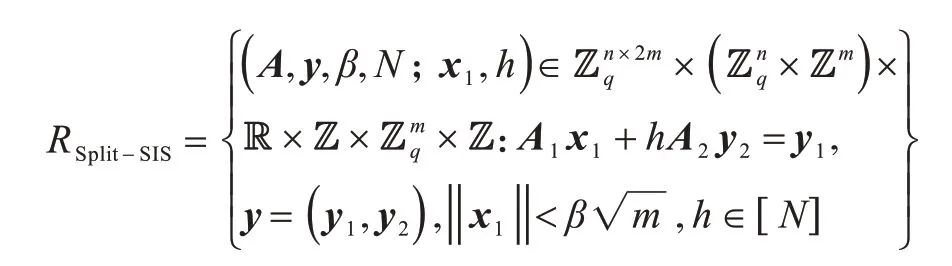
由ISIS和LWE的对偶性可得关于LWE的零知识证明［18］：

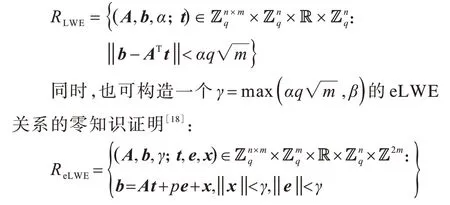
以上零知识证明都可经过Fiat-Shamir变换转换为非交互零知识证明（Non-Interactive Zero-Knowledge Proofs，NIZKP）。

2 格上高效的动态群签名方案

2.1 动态群签名定义和安全模型

2.1.1 群签名定义

一个动态群签名算法［8，13-14，19-20］由以下多项式时间算法组成：

1）GSetup(1n，1N)→pp：输入群签名系统的安全参数n和群成员数量N，算法产生公共参数pp。

2）密钥生成算法：

（1）GKgenGm(pp)→((gmsk，gmpk)，(gtpk，gtsk))：该算法由群管理员执行，输入公共参数pp，生成群管理员的主密钥对(gmsk，gmpk)和追踪密钥对(gtpk，gtsk)。

（2）GKgenUser(pp)→(uski，upki)：该算法由群成员执行，输入公共参数pp，生成群成员的密钥对(uski，upki)。

3）GUJoin(pp，gpk，gmsk)→(certi，regi)：该算法是由群管理员和用户执行的交互式算法，输入公共参数pp、群管理员的主私钥gmpk和群公钥gpk，gpk=(gmpk，gtpk，upki)。若算法执行成功，则群管理员颁发成员证书certi和计算用户的撤销标记regi，用户加入成功。

4）GSig(gpk，uski，certi，m)→Σ：该算法由群成员执行，将(gpk，uski，certi，m)作为输入参数，输出一个由用户uski在消息m上的签名。

5）GRevoke →0/1：该算法由群管理员或用户执行，主要是群管理员将撤销标记加入到撤销列表RL中，并更新和发布撤销列表，若算法输出为1则撤销成功，否则输出为0。

6）GVerify(gpk，m，Σ，RL)→0/1：该算法为确定性算法，并由验证者执行，将(gpk，m，Σ，RL)作为输入参数来判断该签名的签名者是否已被撤销，若未被撤销，则判定该签名是否是消息m上的合法签名，若是，则输出为1，否则输出为0。

7）GOpen(gpk，gtsk，m，Σ)→Idi：该算法为确定性算法，由群管理员执行，输入参数(gpk，gtsk，m，Σ)，返回对消息m做签名的用户者身份Idi。

2.1.2 群签名安全模型

一个群签名方案必须满足正确性、匿名性和追踪性这3个安全特性［6-8，13-14］，其中，正确性是群签名中最基本的要求，匿名性和追踪性是对群签名的安全性要求。

1）在正确性方面，要求方案满足签名验证正确性和签名打开正确性［6-8，13-14］，其中：签名验证正确性是指按算法步骤产生的签名一定能通过验证算法的验证；签名打开正确性是指按算法步骤产生的签名一定能被群管理员打开。

2）匿名性是指任何获得签名的人都不能通过签名判断出真正的签名者身份（除群管理员外）。匿名性又分为弱匿名性（CPA-匿名）和完全匿名性（CCA-匿名）［6-8］。在CCA-匿名的游戏中，敌手能够进行签名打开查询，而在CPA-匿名的游戏中，敌手不能进行签名打开查询。显然，CCA-匿名游戏中的敌手比CPA-匿名游戏中的敌手具有更强的攻击能力，因此，满足CCA-匿名的群签名方案比满足CPA-匿名的群签名方案更安全。本文的群签名方案是满足CCA-匿名的。

3）追踪性是指群成员产生的合法签名能够被群管理员打开，而伪造的签名，即使是由合谋的群成员共同伪造的签名，也不能够被群管理员打开。追踪性又分为CPA-追踪和CCA-追踪，两者的区别在于游戏中敌手是否能够进行腐败查询。本文方案的追踪性是满足CCA-追踪的。

正确性具体的形式化定义如下：

定义7（正确性）对于任意n、N，所有由GKgenGm(·)、GKgenUser(·)、GUJoin(·) 产生的(gpk，certi，gmsk，gtsk，uski)、消息m、i∈[N]，若GSig(gpk，uski，certi，m)→Σ，则GVerify (gpk，m，Σ)=1⇔regi∉RL且GOpen(gpk，gtsk，m，Σ)=Id。i

关于匿名性，下面给出一个敌手A和挑战者B之间的游戏：

1）参数建立。输入任意正整数n、N，挑战者B执行算法GSetup(·)、GKgenGm(·)、GKgenUser(·)、GUJoin(·)产生(gpk，certi，gmsk，gtsk，uski)，并将群公钥gpk发送给敌手A。

2）查询。敌手A可以做签名、撤销、腐败和签名打开查询，查询过程如下：

（1）签名查询：敌手A输入用户身份Idi、任意消息m，签名预言机用(certi，uski)产生用户Idi的签名，并将签名返回给敌手A。

（2）腐败查询：敌手A输入用户身份Idi，腐败预言机返回用户Idi的私钥给敌手A，挑战者B将腐败的用户加入到腐败集合Ua。

（3）撤销查询：敌手A可以查询任意用户的撤销标记，挑战者B将被查询过的标记加入到集合Uc

（4）签名打开查询：敌手A输入(m，Σ)，签名打开预言机返回用户身份Idi。

3）挑战。敌手A选择未被查询的消息m，并同时选择2个用户d0，d1∉Ua∪Uc，其中，用户的私钥和证书分别为，将这些信息发送给挑战者B。挑战者B选择b←R{ 0，1}，用计算挑战签名Σ*，将其发送给敌手A。

4）受限查询。敌手仍可做一些查询，但不能对用户d0、d1做腐败、撤销和签名打开查询。

5）输出。敌手A输出b*。若b*=b，称敌手获胜。

定义8（匿名性）对于任意概率多项式时间的敌手A，若则称群签名方案具有CCA-匿名性。

关于追踪性，下面给出一个敌手A与挑战者B之间的游戏。在游戏中，敌手A的目标是伪造一个签名，管理员利用签名打开算法不能打开伪造的签名。敌手A能够腐化群管理员，在查询阶段也能腐化用户，并可利用加入算法产生一些虚拟成员。游戏过程如下：

1）参数建立。挑战者B执行算法GSetup(·)、GKgenGm(·)、GKgenUser(·)，产生(gpk，certi，gmsk，gtsk，uski)，将群公钥发送给敌手A，并设置Ua=∅。

2）查询。敌手A可以做签名和腐败用户的查询，查询过程如下：

（1）签名查询：敌手A输入任意消息m和用户身份Idi，签名预言机可以返回对应的签名Σ，并将查询过的签名加入到集合Usi（gUsig是由用户身份Idi、消息m和对应消息签名Σ组成的集合）。

（2）腐败查询：敌手A询问任意用户的私钥时，挑战者B将询问过的用户加入到集合Ua，并返回对应用户的私钥。

3）伪造。敌手A利用其所拥有的信息产生一个消息签名对(m*，Σ*)和撤销列表RL*，如果GVerify(gpk，m*，Σ*，RL*)→1，对于Idi∉Ua，(Idi，m*，Σ*)∉Usig，签名打开失败同时GOpen (gpk，gtsk，m*，Σ*)=Idi且Idi∈Ua/RL，则称敌手A获胜。

随着我国的城市化建设不断加快，我国城市与乡村之间的经济水平存在一定的差距，这也使得越来越多的乡村劳动力开始向城市转移，乡村的劳动力大量减少。劳动力的减少使得在山区玉米种植的过程中，田间管理只能由劳动力较低的人群来进行，这在一定程度上影响了田间管理的效果。另外，由于青年劳动力向城市转移，也使得目前山区田间管理人员的受教育程度不足的问题越来越明显，使其在管理过程中难以及时的发现问题和采取科学的方式来解决问题。这样的情况经常会引起玉米产量难以提升、品质也得不到保障。

定义9（追踪性）若对于任意概率多项式时间的敌手A，则称群签名方案具有CCA-追踪性。

2.2 本文方案

本文将文献［11，14］提出的动态群签名思想引入到文献［8］的群签名方案中，提出一个具有加入和撤销机制的格上完全动态群签名方案。该方案包含2个密钥生成阶段：第1个阶段是群管理员的密钥生成阶段，其中使用文献［8］的GPV陷门生成算法和正交抽样算法产生群管理员的主密钥和追踪密钥；第2个阶段是群成员的密钥生成阶段，其中使用文献［11］的离散高斯采样算法，采取满足一定条件的短向量作为群成员的签名私钥。在加入阶段，使用GPV的格基扩展技术和原像采样算法生成群成员证书；在签名阶段，采用和文献［6-8，14］类似的对偶LWE算法；撤销阶段分为用户主动撤销和群管理员撤销群成员，两者共同之处是都将撤销标记加入到撤销列表中。

1）系统建立

GSetup(1n，1N)→pp：n为系统安全参数，N为群成员个数，该算法产生的随机预言机为H：{0，1}*→{ 0，1}t，其中，t=ω(lbn)，A0，，则参数pp={n，N，m，q，s，p，α，β，η，A0，A1}。

2）密钥生成算法

由此可知群公钥gpk=(A，B，F，pp，vi)。

用户先利用PKI中注册过的密钥(pusk[i]，pupk[i])对vi做普通的数字签名：sigi=再将(vi，sigi)发送给群管理员。群管理员验证vi是否已被注册，并且用pupk[i]验证该签名的合法性。若该签名合法或是已被注册过，则终止加入过程；否则群管理员做以下工作：

4）GSig(gpk，usk，cert，m)→Σ

（4）群成员产生一个关于zi并满足(F，vi，β；zi)∈RISIS，的非交互零知识证明π3。

（5）输出签名Σ=(c0，c1，x1，π0，π1，π2，π3)。

5）GRevoke →0/1

（1）若是群管理员执行该算法，则将撤销标记regi加入到撤销列表中，即令RL=RL ∪{regi}，然后发布撤销列表，撤销成功并返回1；否则返回0。

（2）若是用户执行该算法，则将(vi，certi，regi，sigi)发送给群管理员，向群管理员提交撤销申请，群管理员对用户进行身份验证，若验证成功，则将用户的撤销标记regi加入到撤销列表中，RL=RL ∪{regi}，然后发布撤销列表，撤销成功返回1，否则，返回0。

6）GVerify(gpk，m，Σ，RL)→0/1

7）GOpen(gpk，gtsk，m，Σ)→Idi

群管理员使用追踪密钥TB对密文c0解密，得到x0，计算y0=A1x1，y1=Ax0+A0x1，若y0≠0，能够找到一个Idi同时满足y1+Idi y0=ui则该算法输出Idi；否则输出⊥。

3 安全性分析

3.1 正确性证明

对本文方案的验证正确性和打开正确性进行证明。

3.1.1 验证正确性证明

3.1.2 打开正确性证明

3.2 安全性证明

本文方案满足CCA-匿名性和CCA-追踪性，并且能够抵抗陷害攻击。下文将对其匿名性、追踪性、安全性和抗陷害攻击性进行证明。

3.2.1 匿名性证明

定理1在随机预言机模型下，本文方案在LWE假设下是CCA-匿名的。

证明：通过一系列的游戏G0～G5证明。

G0游戏过程如下：

1）挑战者B按照本文方案获得群公钥gpk=(A，B，F，pp，vi)、成员证书certi=(Idi，x0，x1)、群成员的私钥uski=zi，i∈[N]和追踪私钥gtsk=TB，并将群公钥、成员证书和群成员私钥发送给敌手。

2）B初始化撤销链表RL=∅、腐败用户集合Ua=∅和撤销查询集合Uc=∅。

3）敌手A在查询阶段可以对任意用户的任意消息m的签名进行查询，对对应消息上的签名进行打开查询，还可以更新Ua和Uc。

4）敌手A输出选择的消息m*和身份标识Id0，Id1∈[N]，满足Id0，Id1∉Ua∪Uc且

综上所述，在随机预言机模型下，本文方案在LWE假设下是CCA-匿名的。

3.2.2 追踪性证明

定理2在随机预言机模型下，本文方案在ISIS假设下是CCA-追踪的。

证明：假设敌手A多项式时间内攻破本文方案的追踪性，则可构造一格算法C解决ISIS问题，即给定矩阵寻找一个，满足‖x‖≤poly(m)，Ax=umodq。C下一步工作为：

3）查询。敌手A先对用户进行腐败，再做签名查询，过程如下：

（1）腐败。向预言机询问任意用户i∈[N]的私钥，将i加入到集合Ua=∅中，并返回zi。

（2）签名询问。敌手A向预言机询问用户关于消息m的签名，并将签名发送给C。若Idi=i，i∉[N]，则C拒绝接受签名；若Idi=，C对消息m进行签名并利用NIZKP模拟器产生，否则，将在私钥询问阶段中用回答的签名私钥作为Idi对消息m签名。

由以上所证得，C解决ISIS问题的概率至少为ε(ε/qh-2-t)/8m2.5N，若ε是不可忽略的，则ε(ε/qh-2-t)/8m2.5N也是不可忽略的。

综上所述，在随机预言机模型下，本文方案在ISIS假设下是CCA-追踪的。

3.2.3 抗陷害攻击

在本文方案中，用户i的私钥是其通过高斯采样算法采取的短向量zi∈进而选取并计算用户i的公钥若群管理员或其他合谋群成员想伪造i的签名，就必须要产生一个非交互零知识π3，又由于零知识证明π3具有可靠性，不知道zi的群管理员或其他群成员无法产生一个能通过验证的π3，因此本文方案能够抵抗陷害攻击。

4 效率分析

选取以下4个方案：文献［8］格上高效的群签名方案，文献［11］格上具有高效协议和动态群签名的签名方案，文献［13］格上具有本地撤销机制的群签名方案，文献［14］适合大群组的格基动态群签名方案，从公私钥大小、签名大小、加入代价、撤销代价以及是否为完全动态群签名等方面与本文方案进行比较，如表2所示。其中，n为安全参数，N为群成员个数，q∈Z为模数，m=6n1+δ，t=ω(lbn)为零知识证明中证明者和验证者间交互的次数，V为一次签名运算时间，T1为一次随机采样算法时间，T2为一次数乘运算时间，T3为一次特殊采样算法时间（耗时较少的运算如矩阵-矩阵加法、向量-向量加法，运算时间忽略不记）。

表2 不同方案的性能对比Table 2 Performance comparison of different schemes

由表2可知：文献［8］方案中公私钥大小均为O(mnlbq)，签名大小为O(tmnlbq)（t=ω(lbn) ＞1），与群成员数量N无关，但该方案不具有加入和撤销机制，属于静态群签名；文献［11］方案为具有加入机制的部分动态群签名方案，但公钥大小与成员数量相关，不适合大群组的群签名系统，加入过程与本文方案相比虽然减少了1次特殊采样运算，但增加了3nm次数乘运算和2次随机采样运算；文献［13］方案为具有撤销机制的部分动态群签名方案，但公私钥大小、签名大小均与群成员数量N有关，不适合大群组的群签名系统；文献［14］方案是同时具有加入和撤销机制的全动态群签名方案，其签名大小虽比本文方案的签名短，但在加入过程中与本文方案相比增加了4nm次数乘运算时间、2次随机采样算法的时间以及1次特殊采样算法时间，在撤销过程中增加了1mn次的数乘运算时间；本文方案是具有加入和撤销机制的完全动态群签名方案，其加入、撤销代价较小，并且签名尺寸为O(tmnlbq)，公钥尺寸为O(mnlbq)，签名私钥尺寸为O(m)，均与群成员的数量N无关，因此，本文方案也是适合大群组的群签名方案。

5 结束语

群签名的加入与撤销机制及其密钥与签名的长度，始终是密码学领域研究者所关注的重点问题。本文将动态群签名思想引入文献［8］群签名方案，提出一个具有加入和撤销机制的格上完全动态群签名方案。在安全性方面，随机预言机模型下该方案基于ISIS和LWE假设是可证明安全的，能够抵抗量子攻击，同时也能避免陷害攻击；在效率方面，该方案不仅能够实现加入和撤销功能，而且复杂度较低。此外，其签名和密钥长度均较短且与群成员的数量无关。本文方案中群成员的加入需要群管理员颁发数字证书，这会增加群成员的加入开销和数字证书的存储开销，下一步将对此进行改进，设计无证书的动态群签名方案。