考虑煤岩体成拱效应时煤柱塑性区宽度确定

谷拴成，杨超凡，王 盼，薛 蛟

（西安科技大学 建筑与土木工程学院，陕西 西安710054）

煤炭作为1 种重要的工业原料，对国家经济社会发展起着举足轻重的作用[1]，现阶段，我国仍通过留设煤柱的方式对采准工作面进行保护[2]，在煤柱宽度设计中，如何确定合理可靠的煤柱最大塑性区宽度显得尤为重要[3-8]。若选取的煤柱塑性区宽度过大，则留设煤柱宽度的设计也会偏大，这将直接影响到矿井生产的经济效益；若选取的煤柱塑性区宽度过小，则煤柱宽度的设计也会偏小，设计出的煤柱无法承担起防护水、地压等方面的破坏作用，影响回采工作的安全。关于煤柱塑性区宽度计算这一课题，国内外众多学者开展了广泛的研究工作。基于英国的煤矿开采条件，A H 威尔逊在1972 提出了两区约束理论[9]，并给出了煤柱屈服区宽度计算式。王旭春、黄福昌等人[10]通过对煤柱极限强度影响因素分析，建议通过实验确定煤柱塑性区宽度。张少杰、王金安等人[11]根据煤柱破坏特征，采用数值模拟方法，研究了采空区边缘煤岩体塑性区分布形态。谢广祥、王磊等人[12]对煤柱合理宽度进行了研究。刘增平、梁顺[13]在理论计算出煤柱塑性区宽度后对煤柱进行数值模拟研究，根据模拟结果对沿空窄煤柱进行了优化设计。Liya ZHANG，Kazhong DENG 等人[14]利用FLAC3D数值模拟软件研究了煤柱弹塑界面应力增大系数的变化规律及煤柱稳定性。张科学[15]从上区段采空区侧向支承应力分布规律、煤柱应力分布、巷道围岩应力分布、巷道围岩变形与煤柱宽度的关系及护巷煤柱宽度的理论计算5 个方面综合考虑护巷煤柱的宽度。韩承强等人[16]采用现场观测法，分析了沿空掘巷小煤柱以及工作面煤体内应力变化、超前支承压力影响范围, 并通过数值模拟分析了不同宽度煤柱塑性区变化范围。吕晓波[17]采用理论计算和数值模拟对腾晖煤矿合理煤柱宽度进行了研究。目前看来，上述研究在对煤柱塑性区宽度进行确定时，均未能给出确定煤柱应力边界条件的具体方法，为此，以岩土工程中最为常见的成拱效应为切入点，对煤柱受力进行研究，结合煤柱应力边界条件，给出在考虑邻近采空区煤岩体成拱效应时煤柱最大塑性区宽度的计算式。首先对普氏拱的假定[18]进行修正，建立传力拱模型，再对传力拱模型进行分析，确定出拱轴线方程，明确煤柱受力边界条件，据此建立煤柱弹塑性界面微分方程，通过对微分方程求解，推导出煤柱最大塑性区宽度计算式；进一步根据玉华煤矿工程地质条件，采用ANSYS15.0 对煤柱最大塑性区宽度进行模拟研究，探究理论计算结果的适用性；最后结合现场监测结果，对理论计算与数值模拟结果的可靠性进行验证。

1 传力拱模型的建立与分析

成拱效应在岩土工程领域是1 种常见的现象，相关研究[19]认为，岩土工程中的成拱效应是由于岩土材料充分发挥其抗压强度而进行自我优化调整的结果。由于采空区上覆煤岩体不均匀变形受力，煤岩体将自发形成能够调整自身抗剪强度以抵抗外力的拱，该拱必然能使介质最大限度的发挥其抗压强度作用[20]，因此，在采空区上覆岩层自重荷载作用下，合理拱轴线应为二次曲线。

将采空区上方的拱简化为水平拱，认为其处于平面应变状态。基于普氏理论，提出以下假设。

1）采空区上部煤岩体坍塌后所形成的拱只能承受压应力，不能承受拉应力。

2）作用于拱上的荷载仅为上覆岩层自重荷载。

3）拱内垮落的煤岩体将完全填充拱内空间。

4）传力拱物理模型如图1，在邻近采空区侧煤柱侧壁处，将产生破裂面，破裂面与煤壁夹角为θ，θ=45°-φ/2，φ 为煤柱内摩擦角。并在采空区上方的水平面上与传荷拱相交，形成垮落的最大煤岩体。

图1 传力拱物理模型Fig.1 Physical model of force transfer arch

图1 中，b 为传力拱拱高，m；M 为采高，m；a 为采空区宽度的1/2，m；c 为邻采空区侧煤柱垮落煤体的水平宽度，m；a1为传力拱宽度的1/2，m。

基于上述4 个假定，将图1 的物理模型简化为力学模型，传力拱力学模型如图2。考虑到结构对称性，将左半部分拱的作用用水平推力T 代替，选取右半部分拱结构进行分析。

图2 传力拱力学模型Fig.2 Mechanics model of force transfer arch

图2 中，Q 为传力拱上覆岩层自重荷载，N/m；T为作用于拱顶的水平推力，N；R 为拱支座承受的反力；T′为R 的水平分量，N；V 为R 的竖直分量，N；β为V 与R 的夹角，（°）。

任取一点（x，y），根据假定1，由于拱不能承受拉应力。因此所有外力对点（x，y）的弯矩为0，即：

由静力平衡条件可知，作用于拱脚的水平推力T′与作用于拱顶的水平推力T 相等。根据假定3，并取煤岩体初始碎胀系数为K，可得：

式中：K 为煤岩体初始碎胀系数；M 为采高，m；a1为传力拱宽度的1/2，m。

联立式（1）、式（2），可得拱轴线方程为：

当取x=a1时，可得拱高b 为：

根据静力平衡条件可以求得拱支座水平反力T′和竖向反力V 分别为：

由式（3）可知，采空区上方拱的拱轴形式与垮落煤岩体性质以及采空区宽度2a1、采高M 有关，与采空区所处位置埋深无关，这与普氏拱理论所得的结论一致。

但应注意到的是，在对拱轴线的方程进行求解时所采用的假设与普氏拱在求解拱轴线方程时所采用的假设不完全一致。没用采用普氏理论中关于坚固系数f 的假设，在普氏理论中，f 是1 个没有量纲的经验系数，通常取f=Rc/10，普氏将拱脚最大摩擦力降低一半后，利用f 建立了求解拱轴方程的补充条件T′=Qfa1/2。考虑到在煤矿实际生产过程中，由于采用垮落法处理采空区，因此拱内垮落的煤岩体将完全填充拱内空间。根据工程实际建立求解拱轴方程的补充条件式（2）。

2 采空区侧煤帮塑性区宽度计算

推导出采空区上方传力拱的拱轴方程后，进一步对煤柱进行受力分析。煤柱极限强度为σzl，煤柱塑性区宽度为rp，采空区内垮落煤岩体作用于煤壁的水平力为px，建立的煤柱受力模型如图3。

图3 煤柱受力模型Fig.3 Coal pillar model

采空区上覆岩层自重荷载通过采空区上方传力拱向煤柱传递，根据此时煤柱的受力状态，若认为拱脚下的煤柱处于塑性破坏状态，并假定煤柱发生的是剪切破坏，并且剪切破坏面平行于煤层层面，取弹塑性界面微分单元，煤柱弹塑性界面微分单元模型如图4。

图4 煤柱弹塑性界面微分单元模型Fig4 Elastic-plastic interface differential unit model of coal pillar

建立塑性破坏区界面平衡微分方程式（7）。

式中：σx、σy为x、y 方向的压应力；τxy为界面的剪应力；c 为煤柱的黏聚力，Pa；φ 为煤柱的内摩擦角，（°）。

考虑到采空区上方拱向煤柱传力使煤柱发生塑性破坏，建立如下边界条件：

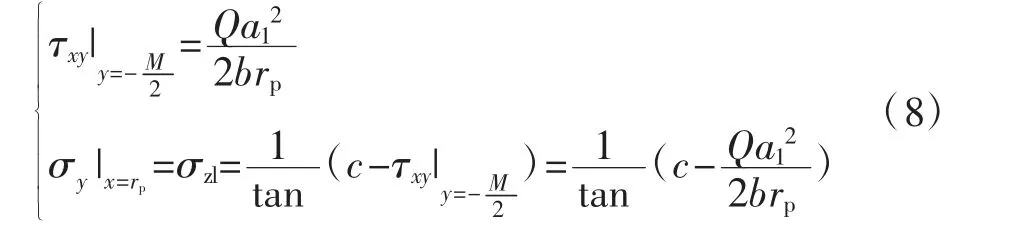
式中：σzl为煤柱极限强度，Pa。

为求解微分方程，还需建立补充边界条件，由于塑性区侧向应力由外向里渐增，在与核区交界处为最大，恢复到开采前的原岩应力[3]，因此可得：

式中：k 为原岩应力场中水平应力系数；ρ 为煤岩体的平均密度，t/m3；g 为重力加速度。

由式（7）～式（9），可得到屈服区宽度rp的表达式为：

式中：px为采空区垮落煤岩体向煤柱侧壁传递的水平压力，N/m；rp为塑性区宽度，m。

根据式（10），可知塑性区宽度在煤柱不同高度处是不同的，在y=0 处煤柱塑性区宽度最大。采空区内垮落煤岩体向煤柱侧壁传递的水平力可以采用岩柱法进行计算，为便于计算，在对整体计算结果影响不大的情况下，忽略扁压作用，则px可由式（11）进行计算。

将式（11）代入煤柱塑性区宽度计算式（9），可计算出煤柱邻近采空区侧塑性区宽度。由式（9）可知，采空区垮落煤岩体向煤柱侧壁传递的水平力px有利于减小塑性区宽度，提高煤柱稳定性。

在实际工程中，考虑到安全方面的要求，若将px作为强度储备，可在计算煤柱塑性区宽度时不予考虑。并取y=0 时煤柱最大塑性区宽度作为留设煤柱宽度计算的依据，并引入采动影响因子d。可得简化处理后煤柱最大塑性区计算式：

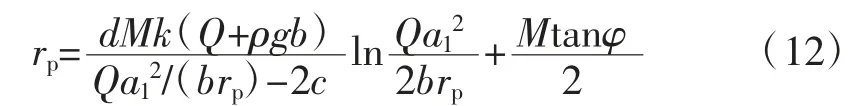
3 模拟验证

3.1 工作面条件

为进一步验证上述理论计算式所揭示规律的合理性，现结合焦坪矿区玉华煤矿2410 工作面开采工况进行模拟验证。

2410 工作面开采范围内煤岩体的初始碎胀系数为1.4，煤层平均厚度为5.9 m，工作面长度240 m。直接顶一般厚度为5.0 m，为粉细砂岩。基本顶一般厚度为12.9 m，为中砂粗岩，成分以石英，长石为主。底板一般厚度为4.1 m，为碳质泥岩。岩层物理力学参数见表1。

表1 煤岩体物理力学参数Table 1 Physical and mechanical parameters of coal and rock

3.2 模型建立

采用ANSYS15.0 进行模拟计算，建立模型时，选取plane42 单元，在划分网格时对煤柱进行网格加密处理，煤层埋深取500 m 和600 m，煤柱宽度取35 m，采高分别取4、5、6、7 m。建模过程中，所用参数值大部分为玉华煤矿实测参数，部分参数由工程类比法确定，数值分析参数见表1。建立的几何模型与物理模型如图5。

图5 数值分析模型Fig.5 Numerical analysis model

3.3 模拟结果分析

模拟结果表明：在采深为500、600 m 时，分别对采高为4、5、6、7 m 时煤柱邻近采空区侧塑性区受力特征进行分析。煤柱等效塑性应力云图如图6。

图6 煤柱等效塑性应力云图Fig.6 Cloud map of equivalent plastic stress of coal pillar

由式（10）可知，煤柱的塑性区宽度在煤柱不同高度处并不相等，在煤柱中间（y=0）塑性区宽度最大，向煤柱顶（y=-m/2）、底（y=m/2）处塑性区宽度递减，数值模拟所揭示的煤柱塑性区沿煤柱高度分布规律与式（10）所反应出的规律一致。

同时，模拟结果表明，当采深一定时，随着采高的增加，煤柱塑性区范围不断扩大；采高一定时，随着采深的增加，煤柱塑性区范围也在不断扩大。模拟结果反应出的规律与式（10）所揭示的煤柱最大塑性区宽度随采高、采深的变化规律一致。

结合铜川焦坪矿区玉华煤矿2410 工作面开采条件，取垮落煤岩体初始碎胀性系数K=1.4，采动影响系数d=1.5，原岩应力场水平侧压力系数k=1.5。将式（12）所计算的煤柱最大塑性区宽度值与模拟结果列表对比见表2。

表2 理论计算与数值模拟结果对比Table 2 Comparison of theoretical and numerical simulation results

由表2 发现，在中等采高（4 m＜M＜7 m）的情况下，依据式（12）得出的理论计算结果与模拟结果相差不大。在采高较小时（M≤4 m），与模拟结果相比，理论计算结果偏小。采高较大时（M≥7 m），与模拟结果相比，理论计算结果偏大。因此，式（12）适用于中等采高情况下计算煤柱的最大塑性区宽度。

4 工程实例

玉华煤矿2410 工作面采深600 m，采高6 m，为中等采高。根据表2 的计算结果，理论计算的玉华煤矿2401 工作面煤柱最大塑性区宽度应为2.63米，数值模拟结果为2.70 m。理论计算结果与数值模拟结果一致。为验证理论计算结果的可靠性，进一步对现场煤柱受力进行监测

4.1 测点布置与数据采集

测站布置在玉华煤矿2410 工作面回风巷道。共安装4 个应力计，安装位置分别距煤壁深1、2、3、4 m。2410 工作面回风巷煤柱应力计安装后，实测煤柱应力变化曲线如图7。

图7 实测煤柱应力变化曲线Fig.7 Measured coal pillar stress change curves

4.2 监测数据分析

在回采过程中，距煤壁1 m 和2 m 深处的应力值呈现先增大后减小的趋势，在回采工作面靠近测站50 m 时，1 m 的煤柱应力开始下降，当工作面推进到距测站9 m 时，该处应力急剧下降，说明此时1 m 处的煤柱发生了塑性破坏；回采工作面靠近测站21 m 时，2 m 的煤柱应力开始下降，当工作面推进到距测站12 m 时，2 m 处的应力急剧下降，说明此时2 m 处的煤柱发生了塑性破坏；3、4 m 深处的应力计读数随着工作面的推进在不断的增加随后保持平稳，表明距离煤壁3、4 m 深处的煤体拥有足够的承载能力，未发生塑性破坏。

实测结果表明，回采过程采空区形成时，煤柱最大塑性区宽度在2～3 m 之间。与理论计算结果2.61 m 以及数值模拟结果2.70 m 一致。结果表明，在中等采高（4 m＜M＜7 m）时，按式（12）确定出的煤柱最大塑性区宽度较为可靠。

5 结 论

1）依据岩土工程中常见的成拱效应，建立了煤矿开采过程中采空区上覆煤岩体的成拱效应模型，并推导出采空区上方形成的传力拱的拱轴方程。

2）依据采空区上覆岩层自重荷载通过传力拱传递至煤柱，建立了煤柱受力模型，对煤柱进行弹 塑性分析，给出了在考虑采空区上覆煤岩体的成拱效应下煤柱的最大塑性区宽度计算公式。

3）理论计算式所揭示的煤柱塑性区变化规律为：①塑性区宽度在煤柱中间（y=0）最宽，并向煤柱顶（y=-M/2）、底（y=M/2）递减；②采空区垮落煤岩体向煤柱侧壁传递的水平力px能减小煤柱的塑性区宽度；③煤柱所在的煤层的采深越大，煤柱的塑性区宽度也越大；④随着采高的增加，煤柱的最大塑性区宽度也会增大。

4）使用ANSYS 数值模拟软件，结合铜川玉华煤矿的工程条件，选取采深为500、600 m，采高为4、5、6、7 m 对煤柱的塑性区进行了模拟。模拟结果表现出的规律与理论计算时所揭示的规律一致。但在煤柱的最大塑性区方面，可以发现在中等采高（4 m＜M＜7 m）时，理论计算的煤柱最大塑性区宽度与数值模拟的结果相差不大。表明在中等采高的情况下，按理论计算式得出的煤柱最大塑性区宽度有较好的适用性。

5）玉华煤矿2410 工作面回风巷道的煤柱受力监测结果表明，随着采煤工作面的推进，采空区形成后煤柱的塑性区宽度在2～3 m 的范围内，与理论计算结果一致，验证了在中等采高下理论计算式的可靠性。