GPS/BDS粒子群优化算法紧组合定位方法及精度分析

陈佩文, 余学祥, 张 浩

(1.安徽理工大学 测绘学院,安徽 淮南 232001; 2.安徽理工大学 矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽 淮南 232001; 3.安徽理工大学 矿区环境与灾害协同监测煤炭行业工程研究中心,安徽 淮南 232001)

近年来,我国北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)快速发展。在此背景下,全球定位系统(Global Positioning System,GPS)与BDS组合定位愈发成为研究热点。相关研究表明,短基线情况下,BDS定位精度与GPS相当,但GPS/BDS组合提高了模糊度固定成功率,增强了定位可靠性[1-4]。

全球卫星导航系统组合相对定位中,依据参考卫星的不同,观测模型大体可分为2类[5]:① 系统内双差模型,即每个系统各自选择1颗参考星,称为松组合模型;② 系统间双差模型,即多系统组合中仅选择1颗参考星,称为紧组合模型。目前,松组合模型已经得到了广泛的研究;而紧组合模型由于仅选择了1颗参考星,引入了系统间偏差(inter-system bias,ISB),若提前求得ISB参数,则可增加组合系统的冗余度,使得定位更为可靠[6-9]。文献[8]研究表明,ISB具有时域稳定性;文献[10]指出,伪距ISB主要由时间和坐标系统差异造成的延迟和硬件延迟组成,且伪距ISB在1 d内是稳定的;由于ISB与模糊度高度相关,因此难以将ISB与模糊度分离开来。针对该问题,结合ISB时域特性,文献[6,11]引入了新的约束条件,定义了新的ISB参数,解决了紧组合定位问题,然而,由于ISB与温度和接收机重启等因素有关[7,12],该方法往往难以满足实时定位的要求。为了实现频率间偏差(inter-frequency bias,IFB)的快速估计,文献[13-15]分析了IFB与次小和最小残差二次型的比值(Ratio)之间的关系,采用粒子滤波的方法求解IFB,实现了GPS与格洛纳斯(GLObal NAvigation Satellite System,GLONASS)的紧组合定位;文献[16]在此基础上,将相位IFB估计问题归结为求解最优化问题,采用粒子群优化(particle swarm optimization,PSO)算法实时求解IFB参数并实现了GLONASS模糊度的固定。本文在上述研究基础上,将求解ISB参数问题归结为求解最优化问题,通过实验验证了PSO算法求解系统间小数偏差(fractional inter-system bias,F-ISB)参数的稳定性;通过设置不同截止高度角模拟卫星受限情况,研究了采用PSO算法实时单历元解算F-ISB参数的紧组合模型,讨论了紧组合模型模糊度固定和基线解算精度的改善情况。

1 数学模型

在GPS/BDS紧组合前,需要对两者进行时空基准统一。GPS采用WGS84坐标系统,而BDS采用CGCS2000坐标系统,2个坐标系统在定义和实现上仅存在微小差异[17],因此,坐标系统的差异在本文中不再考虑。而时间系统方面,由于GPS时与BDS时相差约14 s,可简单采取GPS时减14 s的方式对BDS时进行预处理,不足1 s的微小差异可在站间单差时消除。

1.1 紧组合模型

当站点a、b处接收机对卫星i、j进行同步观测时,双差模型可表示为:

(1)

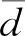
(2)

(2)式即为松组合模型,可见松组合模型实质为紧组合模型的特例。松组合模型中,由于λs2,i和λs1,i大小相等,因此,可将2个单差模糊度合并成一个具有整数特性的双差模糊度。但在异频紧组合模型中,波长不同使得双差整周模糊度不再具有整数特性。为了解决此问题和方便构建统一的紧组合模型,采用模糊度映射的方式构造双差模糊度,使其保持整数特性[18]。

1.2 基于粒子群优化算法的ISB估计策略

(3)

目前,最小二乘模糊度降相关平差法(Least-squares Ambiguity Decorrelation Adjustment,LAMBDA)被广泛运用于整周模糊度的固定,其中次小和最小残差二次型的比值(Ratio)常被用作检验双差模糊度是否固定的标准,而F-ISB作为改正数直接影响整周模糊度的固定,进而与Ratio值存在一定关联。文献[15]研究了Ratio值与F-ISB值之间关系并指出,在F-ISB搜索范围内,Ratio值峰值对应的F-ISB改正值即为最优F-ISB值。因此,可将相位F-ISB估计问题归结为求解最优化问题。本文采用PSO算法求解最优ISB值[16],公式表示为:

(4)

将Ratio值作为PSO算法的适应度值。搜索F-ISB最优值和定位具体流程为:

(1) 初始化粒子(F-ISB)群。

(2) 将F-ISB视为已知值带入(1)式。

(3) 构建法方程,采用LAMBDA算法计算Ratio值。

(4) 利用PSO算法迭代求解最优F-ISB。

(5) 将最优F-ISB值带入法方程,固定模糊度后求解坐标参数。

因此,利用F-ISB与Ratio值之间关系,每个历元可以将F-ISB参数提前求解出来,从而增加观测方程冗余度。

2 实 验

本文选择国内2种品牌接收机A(华测,I70)、B(海星达,IRTK5),共观测5条短基线。基线1为超短基线,长约1 m,观测于2019年9月4日;基线2和基线3长度分别为1 000、3 000 m,观测于2019年9月15日;基线4和基线5均为超短基线,长度分别为1、20 m,观测于2019年9月8日。上述5条基线观测时长均为2 h左右，采样间隔设置为1 s,A、B接收机均接收L1和B1频率。PSO算法各参数值见表1所列。

表1 PSO算法参数

(1) F-ISB稳定性分析。GPS/BDS单历元紧组合整周模糊度及三维坐标标准偏差(standard deviation,STD)统计结果见表2所列。表2中,PDOP为位置精度因子(position dilution of precision)。由表2可知,A、B品牌接收机中5条基线的F-ISB在较长时间内均能保持稳定。其中,与基线2和基线3相比,由于基线1、基线4和基线5为超短基线,架设环境相似,几乎消除了多路径误差、电离层误差及对流层误差等其他误差,因此其STD较小,为1.7～3.0 mm。

基线1～基线5的统计结果表明,随着截止高度角增大,PDOP值和STD值均变大,这是由于可视卫星数减少、模型结构不强所致。按照3倍中误差计算,F-ISB偏差均在0.1周以内。

基线1和基线3的接收机均不变,但是观测时间不同,F-ISB各不相同,说明接收机重启后F-ISB会发生变化,这是由于接收机重启后初始相位变化造成的,因此,接收机重启后,不能将F-ISB视为固定值,需要重新计算,而实时估计F-ISB的算法则无需考虑接收机重启等因素影响。

(2) 实时估计ISB的紧组合算例分析。目前紧组合实现方法普遍将ISB提前估计出来,在随后历元将ISB视为常数,进而实现紧组合算法,但是ISB参数可能与接收机品牌、温度及接收机重启有关[6-7],并且有的接收机ISB毫无规律。实际操作中,由于接收机重启以及温度变化的影响,将ISB视为常数将引入系统偏差,使得紧组合模型定位效果比松组合模型更差,甚至模糊度固定失败以至于不能够定位,因此实时估计ISB显得尤为重要。本文采用PSO算法实时单历元估计F-ISB和坐标参数。

由于基线1、基线4和基线5为超短基线,各项误差基本消除,尽管截止高度角不同,无论是紧组合模型还是松组合模型,模糊度固定成功率均在99%左右。

表2 整周模糊度及三维坐标STD统计结果

截止高度角在40°以下时,松组合和紧组合模型的模糊度固定成功率大致相当。其中,当基线2和基线3的截止高度角从10°变为20°时,松组合模型和紧组合模型的模糊度固定成功率均有大幅提高,这是因为在较低截止高度角时,观测值中含有较多大气误差,从而使得模糊度固定成功率下降。

在较长基线情况下,基于PSO算法的实时ISB估计方法有效提升了模糊度固定成功率。当截止高度角设置为40°时,可视卫星数量迅速减少,平均PDOP急剧增大,由于紧组合模型比松组合模型多了1个观测方程,基线2的模糊度固定成功率由松组合模型的79.96%增加到92.85%,基线3由松组合模型的74.20%提升到90.65%。

截止高度角为45°时,由于可视卫星数量进一步减少,模型结构进一步减弱,松组合和紧组合模型的模糊度固定成功率均大幅减少,但是紧组合模型比松组合模型还是具有较大优势,基线2模糊度固定成功率由松组合模型的19.74%提高到37.99%,基线3由松组合模型的6.73%提高到32.96%。

定位精度方面,基线3单历元紧组合模型定位结果如图1所示。

图1 基线3单历元紧组合模型定位结果

图1中,E向、N向、U向分别为东方向、北方向及天顶方向。由图1可知,基线3截止高度角为20°时,若将松组合静态解视为真值,则单历元紧组合偏差在E向、N向及U向均在1.0、1.0、2.5 cm以内。由表2可知,松组合模型和紧组合模型的三维坐标STD在各种情况下均没有明显差别,最大相差约1.0 mm。由此可见,基于PSO算法紧组合定位精度与松组合定位精度相当,这也从侧面反映了基于PSO算法快速计算ISB值的准确性。

3 结 论

本文采用实时估计F-ISB参数的PSO算法,对GPS/BDS紧组合ISB稳定性、模糊度固定成功率及定位精度进行了研究。实验结果表明,在一定时间内,F-ISB参数具有稳定性,在3倍中误差情况下,F-ISB最大偏差不超过0.1周。不同时间下,采用A(华测,I70)、B(海星达,IRTK5)品牌接收机观测了5条基线,统计结果分析表明,顾及F-ISB参数的实时单历元紧组合模型在1、20 m超短基线中,模糊度固定成功率与松组合模型相比提升并不明显。在1 000、3 000 m长度基线下,紧组合模型有效提升了收星受限情况下模糊度固定成功率,在截止高度角为40°时,1 000 m基线紧组合模糊度固定成功率由松组合模型的79.96%提升到92.85%,3 000 m基线紧组合模糊度固定成功率由松组合模型的74.20%提升到90.65%。在截止高度角为45°情况下,1 000 m基线紧组合模糊度固定成功率由松组合模型的19.74%提升到37.99%,3 000 m基线紧组合模糊度固定成功率由松组合模型的6.73%提升到32.96%。相比于松组合模型,紧组合模型在定位精度方面与其一致,但在较大截止高度角情况下平面仍能保持较好的精度,因此紧组合模型大大提升了定位可靠性。