基于性能的大跨桥梁颤抖振响应概率性评价

2021-02-05邵亚会

合肥工业大学学报（自然科学版） 2021年1期

邵亚会, 海瑞, 钟剑, 赵彤

(合肥工业大学土木与水利工程学院,安徽合肥 230009)

0 引言

结构抗震在基于概率的基础上进行的性能研究目前已基本形成较为完善的体系。桥梁抗风因其复杂性和随机性,目前主要研究仍然集中在风致振动机理的研究。文献[1]提出基于结构性能的抗风方法(performance-bsed wind engineering,PBWE),目前仍处于初步发展阶段;文献[2-3]将基于性能的抗震设计方法引入PBWE,分别采用Monte Carlo法和子空间模拟法对某人行天桥进行基于性能的抗风设计评估;文献[4-5]采用PBWE方法对悬索桥的吊杆和海上风力发电机组进行了设计和研究;文献[6]根据我国大陆地区风压分布特点建立了PBWE理论框架,总结出适应于我国的多级设计风压值、多级抗风性能水准和多级抗风性能目标;文献[7]以基于概率性能的抗震设计理论为基础,建立基于性能的结构抗风设计概率评估框架;文献[8]对薄膜结构的抗风性能进行了概率性的评估,提出薄膜屋盖结构抗风性能概率评估框架。

桥梁的颤抖振响应是桥梁抗风性能研究的重要组成部分,其机理与研究方法也已成熟。现阶段对颤抖振的研究多是定量的,忽略了风场的随机性对颤抖振计算的影响,必然会导致计算结果的偶然性。为确定颤抖振对结构的影响,本文将PBWE方法引入到大跨度桥梁的颤抖振响应的分析中,以江阴长江大桥为例,借鉴美国太平洋地震工程研究中心基于性能的抗震设计方法,考虑风场的随机性,依据规范谱对该桥所处风场进行了模拟,进行了颤抖振响应计算;拟合出该桥不同风速下的最不利部位最大响应曲线;通过对相同风速下多组桥梁跨中加速度响应的分析,代表性提出用正太分布来拟合最不利部位的概率密度,并对该假设进行了验证。基于行车和行人舒适度标准,确定了不同损伤程度的界限,建立了大跨桥梁基于舒适度标准的四级损伤评价标准。对江阴大桥进行分析,计算不同损伤级别下该桥梁最不利部位的损伤概率,通过拟合得到了结构的损伤曲线,为桥梁损伤程度的判断提供了依据。

1 风场模拟与颤抖振分析

1.1 脉动风速场的模拟

依据文献[9],脉动风速在横向和竖向分别采用Davenport谱和Kaimal谱模拟。

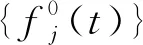
θjm(ωml)+φml)

(1)

对文献[11]中江阴长江大桥桥位所在处进行风场模拟,主梁模拟点数为85,各点等间隔分布,点间距为16 m,频率等分点数为1 024,采样时距取0.1,不考虑导纳函数修正。桥面平均风速为40 m/s时,主梁跨中节点10 min的风速时程如图1所示。

(a) 横向

(b) 竖向图2 跨中节点横向和竖向风速时程

1.2 颤抖振响应分析

抖振是指自然风中的脉动成分引起的随机性强迫振动,现阶段对抖振的计算是针对大气边界层特征紊流引起的结构抖振。在有限元分析中,桥梁结构在空气中运动的控制方程可表示成如下的一般形式:

(2)

其中:M、C、K分别为结构质量、阻尼和刚度矩阵;Fb为等效节点抖振力向量;Fse为等效节点的气动自激力[12]。

通过同济大学风洞实验室得到江阴大桥主梁断面三分力系数CD、CL、CM与颤振导数H*、A*如图2、图3所示。

本文对江阴大桥进行了多风速下颤抖振的时程分析[13],当桥面平均风速为40m/s时跨中加速度时程如图4所示。

图2 主梁断面静风力系数

图3 江阴大桥主梁断面颤振导数

图4 跨中节点竖向加速度时程

2 结构最不利响应的概率分布特征

风场的模拟过程存在随机性,即由于规范谱的分解存在随机性,平均风速相同的情况下,每次得到的风速时程总是不同的,使时程计算结果总是不同。当平均风速为40 m/s时,通过对10组不同的脉动风速时程计算结构跨中竖向位移的最大值可发现:各组中最大加速度均不相同,竖向加速度最大值为3.75 m/s2,最小值为2.19 m/s2,结构加速度响应的变化幅值为41.6%;横向加速度最大值为0.20 m/s2,最小值为0.15 m/s2,结构加速度响应的变化幅值为26.1%。

为了研究不同风速时程下结构的响应规律,取结构最不利部位的加速度进行分析。取平均风速为10～60 m/s分组进行研究,每组取10次不同的脉动风模拟结果进行计算。现给出风速为40 m/s的结构响应曲线,如图5所示,从上到下依次为10组不同脉动风对应的结构响应。

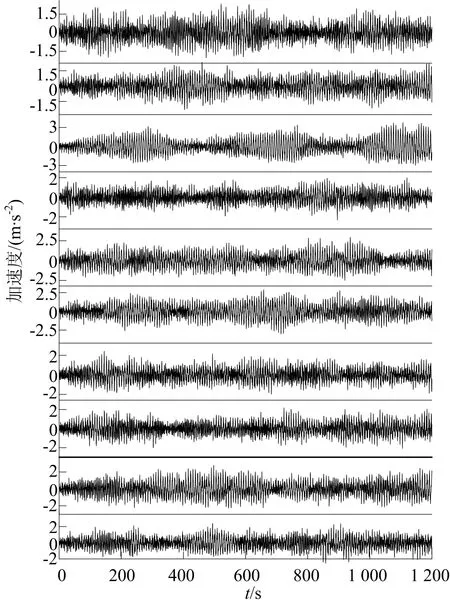
图5 40 m/s风速时竖向加速度时程

通过计算不同风速下各组的加速度时程并对其统计与整理,可得到风速变化时结构加速的均值、标准差等统计参数,见表1所列。

表1 不同风速跨中最大加速度统计表

对上述计算结果进行曲线的拟合,得到结构在不同风速下的最大加速度曲线,如图6所示。

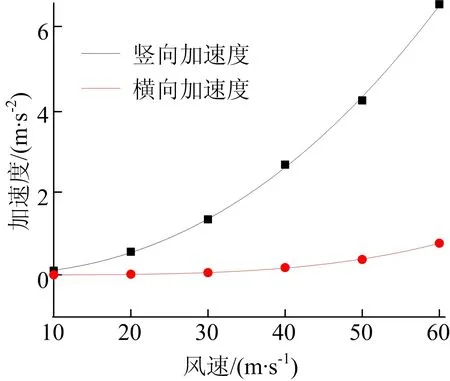
图6 跨中最大加速度曲线

通过对计算结果进行拟合,可分别得到最不利情况下,竖向最大加速度曲线计算公式和横向最大加速度曲线计算公式为:

Y=axb

(3)

对于竖向有:

a=6.052 26×10-4± 9.766 22×10-5,

b=2.267 12 ± 0.040 47;

对于横向有:

a=1.471 93×10-7± 5.063 4×10-8,

b=3.776 23 ± 0.085 09。

对于得到的加速度曲线进行分析,结构跨中最不利部位的加速度最大值均值随风速变化呈幂指数形式增加,即结构的颤抖振响应在恶劣风环境下的变化较良态风环境更加敏感;对于竖向和横向加速度曲线进行分析,结构在竖向的加速度响应全风速下均大于横向。随着风速不断增加,竖向加速度响应变化幅值也大于横向的变化,故结构在竖向的结构响应较横向更加敏感。运用该曲线可计算出任意风速下结构跨中加速度最大值的均值,为结构响应的概率性分析提供了依据。

同一风速下,确定结构最不利部位的最大响应符合何种分布是计算结构损伤概率的基础。现阶段对大跨桥梁最不利部位的最大响应分布并没有统一意见。为研究结构不同风速下结构响应的概率分布,代表性地取其分布为正态分布。本文分别对30 m/s和40 m/s风速下10组结构的加速度响应峰值进行拟合,验证其概率分布的类型，得到其概率分布Q-Q图如图7、图8所示。

从图7可以看出,当结构所受平均风速相同时,其竖向加速度和横向加速度总是围绕其标准线呈均匀分布,基本符合一条直线,可得到结构最不利部位的加速度最大值在竖向和横向总是服从正态分布。

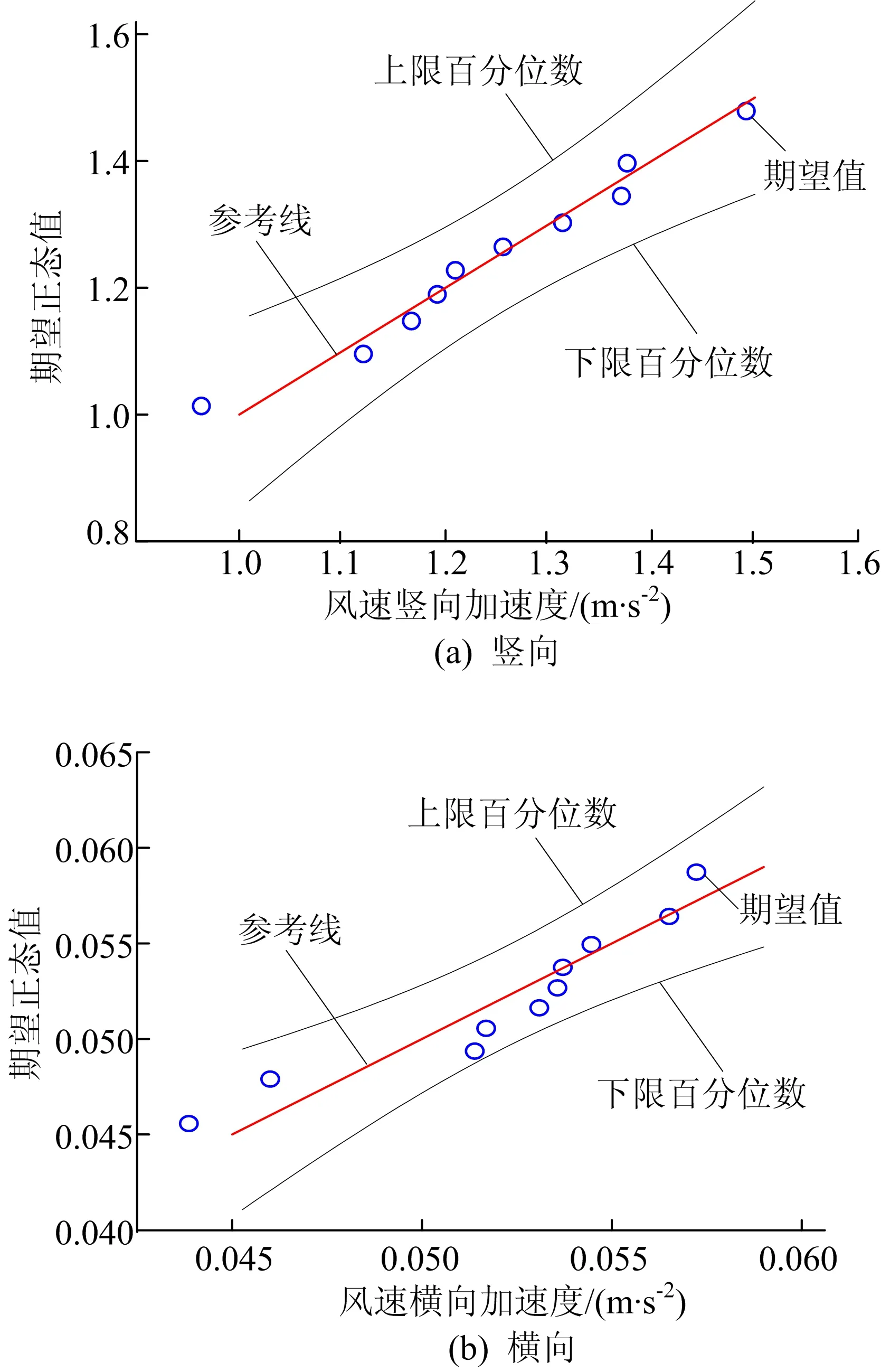
图7 30 m/s风速下结构加速度响应Q-Q图>

图8 40 m/s风速下结构加速度响应Q-Q图

通过对图7、图8结构加速度响应Q-Q图分析,当结构所受平均风速不同时,相同方向下结构最不利部位的加速度最大值总是围绕其标准线呈均匀分布,基本符合一条直线,即可认为结构最不利部位的加速度最大值总是服从正态分布且与结构所受平均风速的大小没有关系。

综合上述计算和验证结果,可根据同一风速下结构的均值和方差拟合出该风速下结构响应的概率分布曲线,用于计算结构响应超越某界限的概率值,得到结构的损伤概率。现给出40 m/s风速下竖向加速度响应概率分布图如图9所示。

图9 40 m/s风速竖向加速度响应概率分布

该曲线拟合时,取频数分割间距为0.01。通过该概率分布图,可计算出任意加速度界限下结构在该风速时的损伤概率。

对于其余风速未给出计算响应的均可通过图7中拟合所得公式计算出结构加速度最大值的均值。通过给定变异系数的均值可求解结构加速度响应最大值的标准差。依据所得均值与标准差就可拟合出结构在该平均风速下的概率分布曲线。

3 桥梁颤抖振易损性曲线和概率评价

3.1 评价标准的界定

抖振是一种强迫振动,在各风速下均可能发生,但其往往不会引起结构毁灭性的破坏。国内外现阶段对抖振响应的研究现阶段多集中于荷载振动引起的疲劳和抖振对不同桥型产生的影响。桥梁作为交通枢纽,往往是一个国家或一个地区的交通命脉,有交通量大、交通组成复杂等特点。在破坏范围内的振动,尤其是长距离的交通运输往往会对行车和行人的舒适性产生影响。文献[9]依据模拟试验将行人舒适度分为“非常好”、“好”、“一般”、“差”、“无法忍受”5个等级;同时对于行车舒适度也给出了评价标准:竖向加速度aw峰值不大于3.6 m/s2,横向加速度au峰值不大于2.4 m/s2。

对于行人舒适度的各级评价标准划分见表2所列。

对大跨度桥梁影响概率P而言,其影响因素是复杂多变的,若将其影响因素产生的概率用数值的形式可表示为:

P=(a1,a2,a3,a4,…)

(4)

结构损伤的概率则可以表示为:

Pd=1-Pmax(a1,a2,a3,a4,…)

(5)

其中:Pd为结构的损伤概率;Pmax(a1,a2,a3,a4,…)为各种影响因素下结构在该等级评价标准上限的累计概率。

基于行人舒适度的评价标准,本文将结构损伤程度分为4个等级:等级1时竖向加速度aw>0.3、横向加速度au>0.15;等级2时竖向加速度aw>0.85、横向加速度au>0.4;等级3时竖向加速度aw>1.45、横向加速度au>0.65;等级4时竖向加速度aw>2.0、横向加速度au>0.9。

3.2 基于行人舒适度的损伤评价

任意影响因素对结构损伤的概率都是不同的,单一因素对结构产生的影响可通过上述评价标准,通过计算不同风速下的累积概率得到。对于行人舒适度而言,结构发生颤抖振时随风速变化时的各级损伤曲线[14-16]如图10所示。

对得到的基于行人舒适度评价标准的损伤曲线进行分析可知，随着风速的不断增加,结构在该等级下的损伤概率也不断增加。依据文献[11],江阴长江公路大桥设计风速为40.8 m/s。对于竖向损伤,损伤程度最高的四级损伤在风速为30 m/s2时其损伤概率仍然为0,风速在30～40 m/s2时其损伤概率增长迅速。对于横向损伤,当结构处于良态风荷载作用下时,最低损伤程度的一级损伤在较高风速下损伤概率较高外,其余等级的损伤概率均为0。综合对比图10a和图10b可知,相同损伤等级时风速增大,竖向损伤总是比横向损伤对风环境更加敏感,即结构的损伤主要由竖向损伤控制。

综合考虑上述2个方向的损伤曲线图10a、图10b可以看出,结构在良态风荷载产生的颤抖振作用下,行人舒适程度较差但处于可承受范围内;结构在风荷载产生的颤抖振作用下,行人舒适度的损伤由竖向结构响应控制。

3.3 基于行车舒适度的损伤评价

对行车舒适度而言,基于加速度的评价标准较为简略。可定义其对桥梁损伤程度标准为:竖向加速度峰值aw>3.6 m/s2,横向加速度峰值au>2.4 m/s2。考虑行车舒适度时,结构发生颤抖振时随风速变化的损伤曲线如图11所示。

对得到的基于行车舒适度评价标准的损伤曲线进行分析可知,在良态风荷载产生的颤抖振作用下,竖向和横向的损伤程度均较小,结构行车舒适度高。对比竖向损伤曲线和横向损伤曲线可以发现,随着风速的增加,竖向损伤对风荷载的作用更加敏感,横向竖向损伤对风荷载产生作用的损伤较缓慢,则风荷载作用下,结构颤抖振对行车舒适度的损伤程度主要由竖向响应控制。