平均数 教学设计

苏丽华

教学内容：

平均数

教学目标：

1、创设学生熟悉的情境，使学生理解平均数的意义，知道平均数的求法，了解平均数在统计学上的意义。

2、经历探索求平均数的方法，初步感知“移多补少”在数学中的作用。

3、通过利用平均数解决问题，提高学生的统计意识，感受平均数在生活中的应用价值，增强应用数学知识解决问题的能力。

教学重、难点：理解平均数的意义，掌握平均数的求法。

教学过程：

一、导入

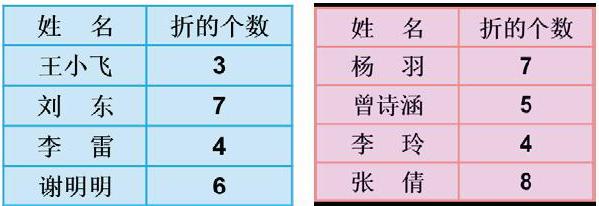
放学后，同学们分成两组进行折星星比赛。这是一分钟内大家折的情况。

怎么判定谁赢谁输？生1：算出两队的总成绩，进行比较，谁折的多谁赢。

好办法，赶紧算算。

生：男生队：20个 女生队：24个 24个>20个，女生队赢。

女生队非常厉害，多折了4个，赢得了比赛。还有其他方法吗？

生2：直接比 7和7抵消，4和4抵消，3和5比，6和8比，女生队赢了。

两种方法虽然不一样，但都是在比男生和女生折星星的个数。你们太棒了！

二、新授

（一）制造冲突，引出平均数

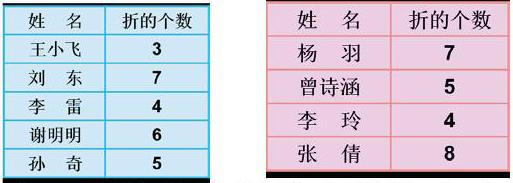
1、男生队又派了一位队员上场，补上了差的4个，还反超了，这回赢了吧？

生：虽然男生组的个数比女生队多了，但男生队多一个人，对女生队不公平。

那怎么办？

生：可以让女生队再派一个人，然后再算总数，就行了。

如果女生队不再补充人数，怎么比较？生：人数不同就得比平均数，才公平。

由于两队人数不等，比总数定胜负就不公平了。就像你们所说，这种情况下，我们可以利用平均数作为标准进行比较。今天我们就来学习有关平均数的知识。

（二）理解含义，探究方法

1、我们先来看女生队的数据。为了便于观察，我给你们准备了示意图。我们简称这四位同学为A、B、C、D，你从图中看出什么了？

生：能看出每个人折的星星个数;C折的最少，D折的的最多;A比B多……

2、刚才你们要求平均数，你觉得平均数是什么意思？

生：平均每人折了多少个星星。

小组讨论求出女生队的平均数。可以利用表，也可以利用图。

哪个组能说说你们的方法？

3、刚才我们通过移多补少和列式计算两种方法，求出女生队平均每人折了6个星星。平均数是6，是不是代表每个人都折了6个呢？

生：不是，6不是每個人实际折的星星数量，他们折的有多有少，都不相同。

既然平均数6并不能代表每个人实际折的数量，那它代表什么呢？

生：平均数代表的是女生队的平均水平（总体水平、整体水平）。

没错，这里的6，不是每个人真正折的数量，但它能够反映女生队的总体水平，或者说是这组数据的集中趋势，所以我们说，平均数具有一定的代表性。

4、仔细观察平均数和每人实际折的星星数之间有什么关系？

生：有的比平均数多，有的比平均数少。平均数比最大数少，比最小数多。

小结：你们真棒，不仅理解了平均数的含义，还知道了求平均数的方法。

5、现在知道哪个队获胜了吗？

生：还不知道。我们只求出了女生队的平均成绩，男生队的成绩还没求呢。

你能独立解决这个问题吗？说说你们是用什么方法求平均数的？

生：（3+7+4+6+5）÷5=5 5﹤6，所以女生队获胜了。

生：计算：总数÷人数=平均数 移多补少：7给3两个，6给4一个。

通过分析，男生队输的心服口服。解决这个问题时，为什么要求平均数？

生：两组人数不同，所以不能只比总数，用平均数比较就公平了。

平均数表示什么？生：平均数表示平均每人的数量，是这组数据的平均水平。

平均数是刻画一组数据的集中趋势的统计量，是统计中最常用的一个指标，它既可以描述一组数据本身的总体情况，也可以作为不同组数据比较的一个指标。

6、平均数的敏感性

（1）如果女生队再加一个人E，你觉得平均数会有什么变化？

生：如果她折的个数比6度多，平均数就会变大，如果她折的个数比6少，平均数就会变少。

（2）采访一下女生们，如果E同学折了1个，你们愿意吗？为什么？

（3）逆向思维

（三）感受生活中的平均数

生活中你还在哪些地方或什么事情中遇到或用到过平均数吗？举例说一说。

生：平均气温、平均身高、平均体重、平均成绩、平均时间……

四、三、总结：你有什么收获？