基于主元分析- 概率神经网络的车辆受电弓故障诊断*
2021-02-04刘若晨
王 宇 刘若晨
(江苏理工学院交通运输系,213001,常州∥第一作者,助教)
受电弓的可靠性直接影响城市轨道交通车辆的安全运行。目前的人工定期检修维护受电弓的方式已不能满足城市轨道交通发展需求,迫切需要新的受电弓诊断检修方法。同时,在受电弓日常检修中,存在大量过程数据及故障数据未被深度挖掘,这些数据可为检修决策提供指导。
随着人工智能技术的发展,设备故障诊断技术也在快速发展。文献[1]采用蛙跳算法和过程神经网络结合的方法对推油机进行故障诊断。文献[2]将自适应模糊神经网络应用于发动机的故障诊断研究。文献[3]基于高斯RBF(径向基函数)神经网络建立了轨道交通车辆齿轮箱故障诊断模型。文献[4]以模糊理论及自适应网络为基础搭建了城市轨道交通车辆牵引供电系统故障诊断模型。文献[5]以聚类分析为基础,对高速铁路信号故障进行聚类集成、特征选取,从而实现诊断。小波包络及贝叶斯网络等方法也被应用到铁路车辆设备故障诊断中[6-9]。上述文献的方法为城市轨道交通车辆受电弓的故障诊断提供了思路。文献[10]通过片段跟踪算法实现对受电弓系统的状态进行监测。文献[11]基于电动机电流及受电弓工作距离的监测对受电弓碳滑板磨耗量进行预测估计,实现提前维护。文献[12]提出了基于BP(反向传播)神经网络的受电弓接触线磨损及应变估计诊断模型。但上述诊断方法需利用在线监测数据进行故障诊断,而目前尚未有相关在线监测设备能够提供城市轨道交通车辆受电弓的在线监测数据,同时在日常检修过程中存在大量故障及检修数据均未得到合理利用的情况。本文引入主元分析法对检修过程数据进行预处理,在此基础上建立概率神经网络模型,将主元分析与概率神经网络相结合进行受电弓的故障诊断,为检修决策提供建议。
1 受电弓工作原理及故障分析
本文选用上海轨道交通某线路车辆单臂式气动受电弓为对象进行分析。该受电弓主要由弓头、上支架、平行导杆、液压减振动器、下支架、连接杆、气动设备、最低位置传感器、底架等组成,如图1 所示。
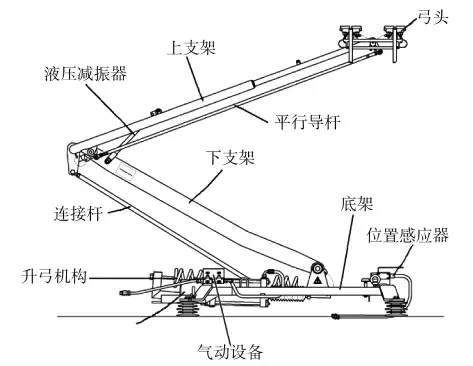
图1 单臂式气动受电弓结构图
城市轨道交通车辆受电弓升起后与架空接触网接触,从接触网获取电流并传递给车辆电气系统。电流由接触网流入到弓头,依次经过上臂杆、下臂杆流入底架,最后经连接板、车顶母线进入车辆电气系统。
升弓操作时,启动空气压缩机,当达到受电弓的额定工作气压时,按下升弓按扭,压缩空气由电磁阀、控制箱进入空气弹簧,气动设备推动钢丝绳带动下臂杆运动,托起受电弓上臂杆,弓头平稳运动升至接触网高度,完成升弓。
降弓时,受电弓控制箱将空气弹簧中的压缩空气释放之后,在重力作用和液压减振器的辅助下,受电弓平稳落位至底架上的橡胶止挡,完成降弓动作。
根据对该型号受电弓日常检修维护记录的总结分析,结合单臂式气动受电弓的故障模式及其机理分析,可将受电弓的故障形式归纳为受电弓不能升起、状态显示不匹配、弓网拉弧、受电弓部件受损、受电弓无法响应5 种类型。
2 受电弓状态数据的采集与预处理
2.1 受电弓状态数据的采集
考虑因线路条件不同而引发不同故障情况的因素,以及车辆检修长时间积累的大量故障数据资源不能得到充分利用,本文以受电弓结构、工作原理、故障模式及失效机理为基础,选取均日常运营状态数据(如平均时速、运行里程、工作电流、最大升弓高度等)以及均衡检修中的过程数据(如碳滑板的磨损量、分流导线状态、弓网接触压力等)中18 个特征参数向量X=[x1,x2,…,x18]作为初始数据,如表1 所示。
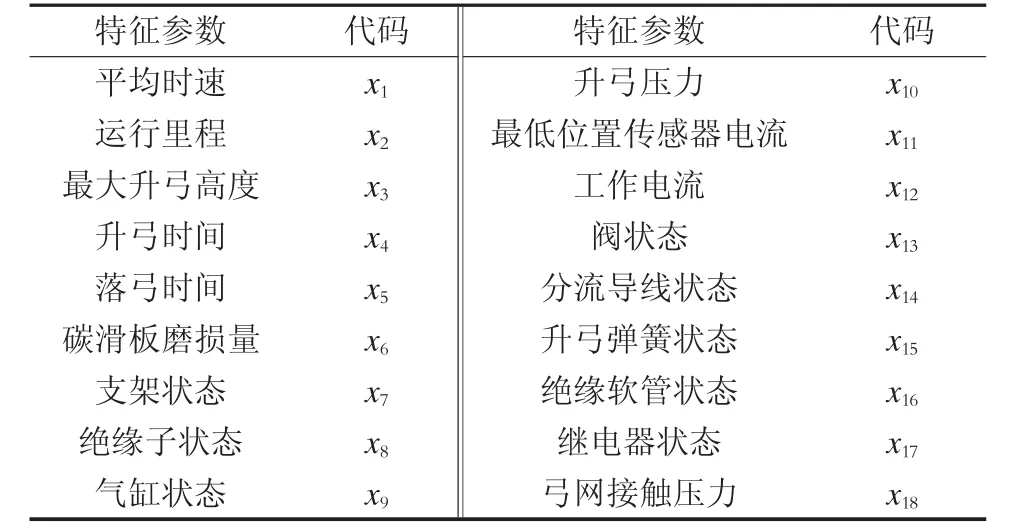
表1 受电弓初始特征参数
2.2 主元分析法
由于采集的受电弓初始状态数据涉及参数变量较多,本文选用主元分析法对其进行降维处理。
主元分析(PCA)法是一种用相对较少但携带信息足够的特征变量来反映多个相关变量的转化方法[14]。在保证诊断正确率的前提下,对冗余和噪声进行剔除,进而实现原始特征数据变量的降维,减少诊断耗时,提高诊断效率。计算过程如下:
1)构建原始变量矩阵X0∈R。矩阵的行xi对应原始数据样本,矩阵的列xj则对应不同的被测量。由于初始数据的量纲不同会导致变量结果分散严重,因此需对观测样本进行标准化处理。
2)对处理后的矩阵X0进行协方差求解,即进行相关系数矩阵R 的计算。即:
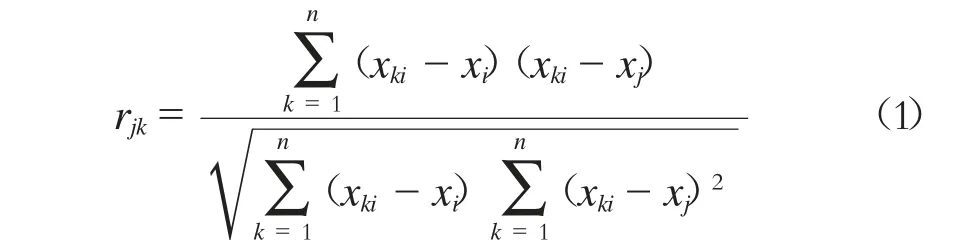
式中:
rjk——标准化后变量xj和xk的相关系数矩阵;
xki——矩阵第i 行第k 个向量。
4)将特征向量转化为主元元素,计算主元贡献率及累计贡献率。
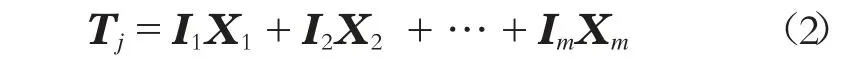
式中:
Tj——第j 主元,代表矩阵X 在对应主元特征向量上的投影,对应的覆盖范围越大,其投影长度会越长。若主元Tj递减,则I1即为覆盖信息程度最广的方向。
5)计算累计贡献率α。
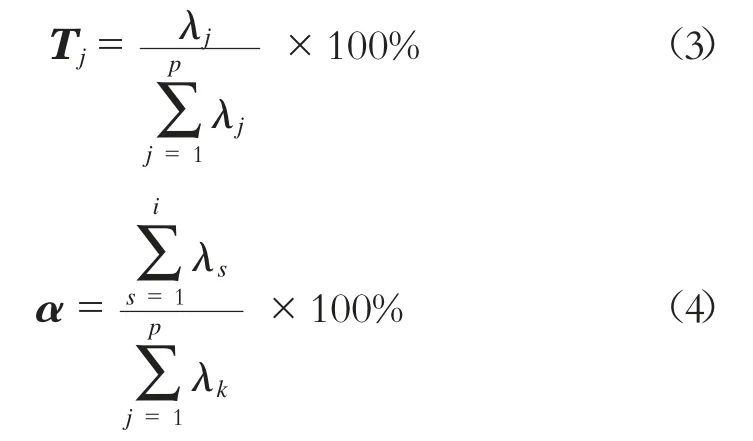
式中:
λj——j 主元特征值;
λs——s 主元特征值;
λk——k 主元特征值。
一般而言,累计贡献率α 达到85%主元即认作是包含绝大部分主要信息的主元元素。
2.3 基于主元分析的状态数据预处理
在初始采集数据中,支架状态、绝缘子状态、气缸状态、分流导线状态、绝缘软管状态、升弓弹簧状态及继电器状态若处于损伤、裂纹或失效状态下则记为“0”,无损状态记为“1”。平均时速、运行里程、最大升弓高度、升落弓时间、碳滑板磨损、升弓压力、最低位置传感器电流、工作电流、弓网接触压力等由于变量涉及量纲之间差异较大,采用归一化对初始数据进行处理,最后对18 个特征参数进行主元分析,得到对应各主元的参数变量为X=[x1,x2,.…,x18]。各主元贡献率由大到小排列如表3。
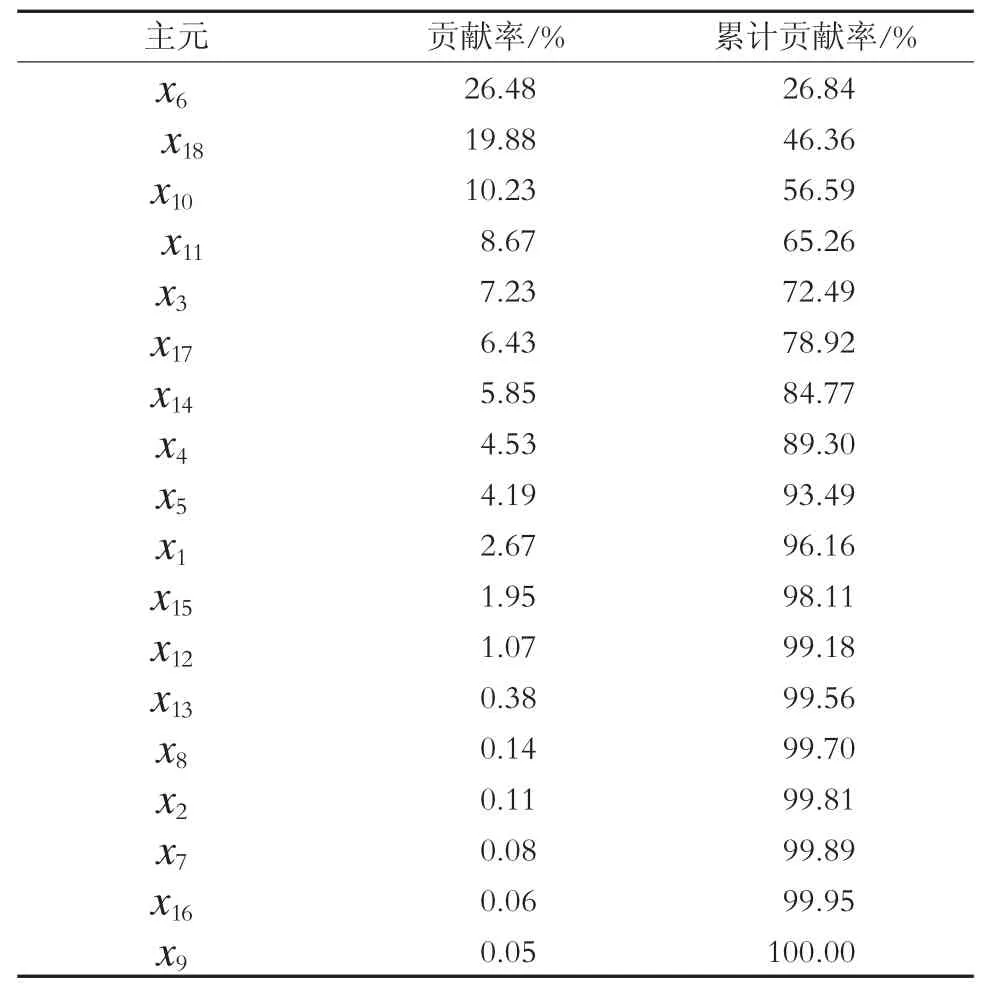
表2 各属性主元贡献率
由表3 可知,12 个主元即可包括99.18%的参数特征信息。因此,本文依据主元分析法将18 个特征变量X′降维至12 个。新的特征变量为X1=[x6,x18,x10,x11,x3,x17,x14,x4,x5,x1,x15,x12]。各主元贡献率变化如图2 所示。
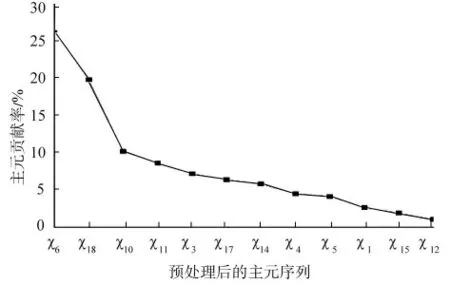
图2 各主元贡献率
3 基于概率神经网络的受电弓故障诊断
将经主元分析预处理后的特征变量X1输入到概率神经网络模型中进行训练与测试,对受电弓状态进行判定。
3.1 概率神经网络
不同于传统BP 神经网络,概率神经网络(PNN)是一种以指数函数作为激活函数的前馈神经网络。以贝叶斯决策和密度函数估计理论为基础[15],共包括输入层、模式层、求和层及输出层4 个部分[16]。网络结构如图3 所示。
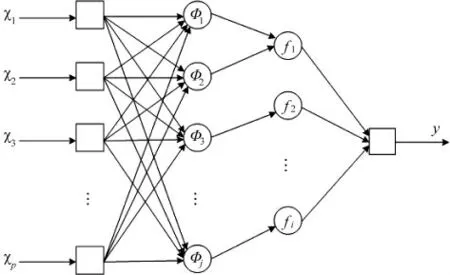
图3 概率神经网络结构图
数据样本的原始特征参数以x 的形式由输入层输入,与权值wi相乘,得标量值zi,并将所得结果输入到模式层。

模式层中的神经元节点数目取决于对应输入样本数,且每个神经元节点包含一个中心。以函数exp[(zi-1)]/σ2为激活函数,模式层中第i 个样本的第j 个神经元所对应的输入输出关系为:
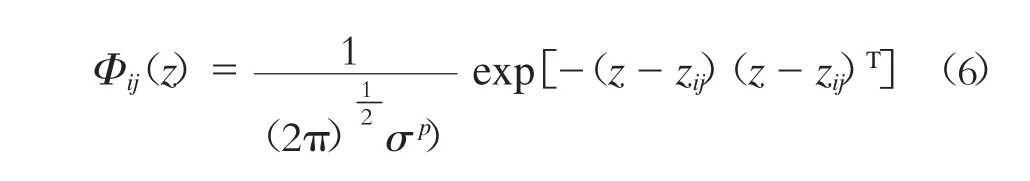
式中:
σ——平滑因子;
p——数据样本的维度;
zij——第i 个样本第j 个中心;
Φij——模式层i 样本的第j 神经元对应的输出。
在求和层中,分类类别数目与神经元个数相对应。在本文中对应于5 种故障状态和正常情况。求和层对模式层中同类别的隐含神经元输出取加权平均,求得其概率密度。即:
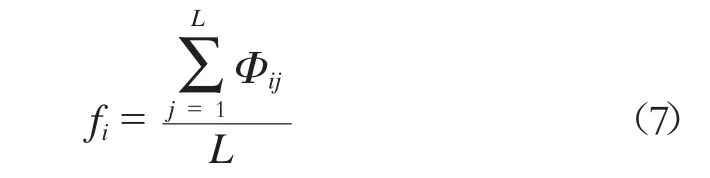
式中:
L——第i 神经元的数目;
fi——概率密度输出。
最后根据贝叶斯决策的分类规则,各类别对应概率的评估,将最大后验概率类别作为输出类别由输出层输出。
3.2 受电弓故障诊断
本文以日常检修过程数据及故障数据样本中的123 组数据为训练样本,40 组数据为测试样本,对受电弓的正常状态和5 种故障状态进行模型诊断训练和测试。每种状态的样本数目如表3 所示。
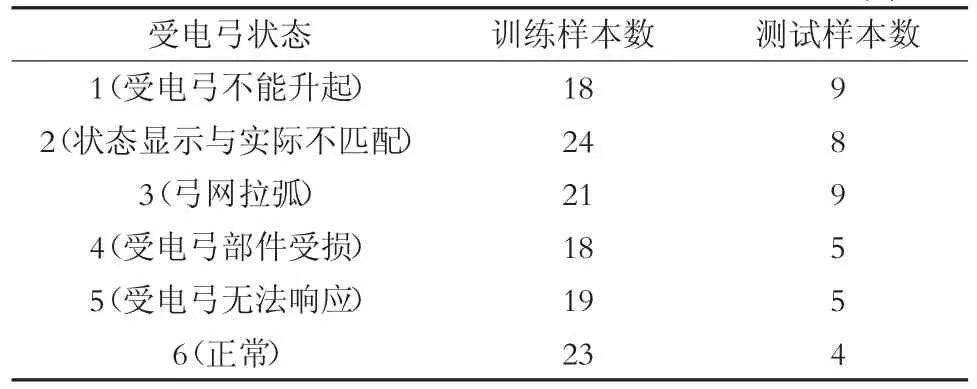
表3 不同受电弓状态的样本数 单位:组
图4 为未降维的特征变量输入概率神经网络模型后的诊断结果。

图4 PNN 诊断结果
将降维后的特征变量X1=[x6,x18,x10,x11,x3,x17,x14,x4,x5,x1,x15,x12]代入概率神经网络故障诊断模型中,所得结果如图5 所示。
降维前后PNN 和PCA-PNN 诊断模型结果差异对比见表4。
由表4 可见,未经主元分析降维处理的PNN 的诊断模型诊断耗时5.38 s,诊断正确率为85%。包含12 个主元的PCA-PNN 诊断模型的诊断时长为2.93 s,诊断正确率达到95%,很大程度上提高了模型的诊断正确率。因此,通过主元分析对初始数据进行降维预处理不仅可以减少诊断耗时,在一定程度上还可提高模型的诊断正确率。研究受电弓系统时,可选取主元分析法和概率神经网络相结合的方法进行故障诊断,准确率高且耗时短。
4 结论
1)采用主元分析法对原始特征参数进行降维,降维后的特征参数可包含绝大部分原始信息,有效缓解了原始样本数据维数过高的问题。
2)针对本文研究的受电弓系统故障诊断,PNN诊断模型诊断正确率为85%,PCA-PNN 诊断模型诊断正确率为95%,经过主元分析降维处理后的诊断模型正确率明显高于直接使用概率神经网络进行诊断的模型。
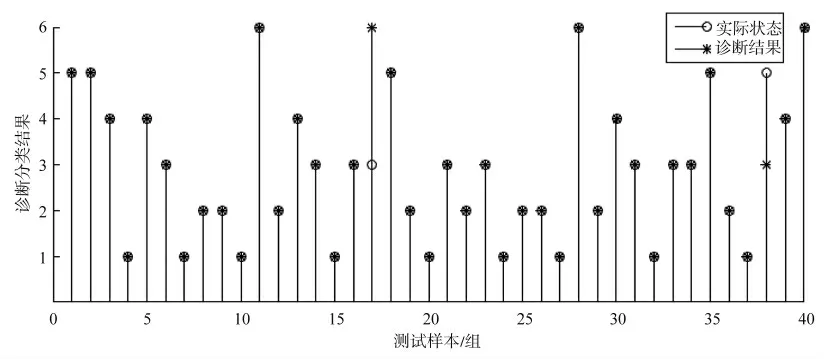
图5 PCA-PNN 累计贡献率99.68%诊断结果

表4 特征变量降维前后诊断结果对比
通过主元分析法对城市轨道交通车辆受电弓检修及故障数据的处理,结合概率神经网络模型进行故障诊断,提高了诊断的正确率,解决了城市轨道交通车辆受电弓故障诊断的问题,为检修决策提供参考,同时也为复杂系统的故障诊断提供思路。
