基于快速沃尔什-哈达玛变换的OVSF 码盲识别算法

刘剑锋，郭晋宏，王光育，徐国微，冯 华

（1.中国人民解放军92773 部队，温州325800；2.中国人民解放军92512 部队，宁波315100）

引 言

正交可变长扩频因子码（Orthogonal variable spreading factor，OVSF）由Adachi 于1997 年提出，已经被3GPP［1-2］标准化组织采纳为地面商用第3 代移动通信系统支持多速率业务的主要方案之一。OVSF 码的可变长特性可以满足通信中的多速率业务要求，而其正交性质则可以减小不同物理信道之间的相互干扰，它为宽带码分多址（Wideband code division multiple access，WCDMA）通信系统提供高度灵活的业务起了非常重要的作用。OVSF 码技术作为一种典型的可变扩频增益多速率技术，它具有可变扩频增益的特点。WCDMA 系统采用OVSF 码作为信道化码，为其提供高度灵活的业务起了重要作用。

近年来，出现了一系列针对OVSF 码的研究成果，文献［3-8］研究重点均基于OVSF 码的正向分配，并未涉及OVSF 码的反向识别。在合作通信情况下，合作接收方可以预先获得信道中OVSF 码的分配信息，无需OVSF 码的反向识别便可实现信号的解扩。但是出于技术保密和军事用途的非合作通信，OVSF 码分配信息未知，作为非合作接收方要实现信号解扩，首先要获取信道中OVSF 码的使用情况，因此OVSF 码识别技术在非合作通信中至关重要。OVSF 码盲识别是指在完成小区同步［9-14］的基础上，在非合作和无先验信息的情况下获得WCDMA 下行链路OVSF 码的使用分配情况，继而对WCDMA 信号进行盲解扩，因此OVSF 码盲识别研究具有重要的军事应用前景。

现有的研究文献大多是针对WCDMA 系统物理层的信号模型、信道估计和接收关键技术方面的研究。文献［15-16］主要是在合作通信情况下针对一般的伪随机扩频码进行研究，而对非合作情况下OVSF 扩频码的盲识别研究并不多。文献［17］针对低信噪比情况提出了一种利用WCDMA 信号的相关矩阵累加平均与其奇异值分解相结合的OVSF 码盲估计算法。这种算法因为存在相位反转会导致识别结果存在模糊性，而且由于要进行大量的相关矩阵累加平均和奇异值分解运算，计算量较大，无法满足工程上快速识别要求，同时该算法只适应于单用户情况，对信道中存在多个OVSF 扩频码的情况没有进行深入研究。如果能实现非合作、低信噪比和低计算复杂度的OVSF 码盲识别，将对WCDMA军事通信信号侦察和WCDMA 信号非合作接收方面的应用具有及其重要的意义。

本文针对非合作通信和低信噪比情况下，在深入研究OVSF 码递归构造原理、码树结构模型、数学理论基础以及分配原则的基础上，利用OVSF 码与Hadamard 矩阵的关系以及自身的继承与正交性，提出了一种基于快速沃尔什-哈达玛变换的OVSF 码盲识别算法，该算法采用数据的循环移位消除了识别结果的模糊性，采用快速沃尔什-哈达玛变换降低了计算复杂度，在无先验信息和低信噪比条件下，可在8.2 ms 内完成20 个OVSF 扩频码的同时识别，识别准确率在95%以上，具有很高的工程与军事应用价值。

1 OVSF 码的数学模型

本文采用Hadamard 矩阵导出OVSF 码结构。一阶和二阶的Hadamard 矩阵分别定义为［18-19］

高阶Hadamard 矩阵可由低阶Hadamard 矩阵按如下方式递推构造［18-19］

由式（3）可知，Hadamard 矩阵是一个N ×N 阶的正交方阵，阶数按N =2k，k=0，1，2，…的规律排列，高阶Hadamard 矩阵可以由低阶Hadamard 矩阵递推得到。Hadamard 矩阵中的每一行，对应着一个Walsh 函数，因此利用HN就可以很方便地构造离散Walsh 函数，该函数有严格的继承关系。

将一个m 阶的Hadamard 矩阵记为Cm，Cm是一个m×m 的方阵，其中m=2n，n=0，1，2，…，N -1，Cm中每一个行向量记为cm，k，k=1，2，…，m，则Cm可以表示成如下m×m 矩阵

将Cm按式（4）递归构造

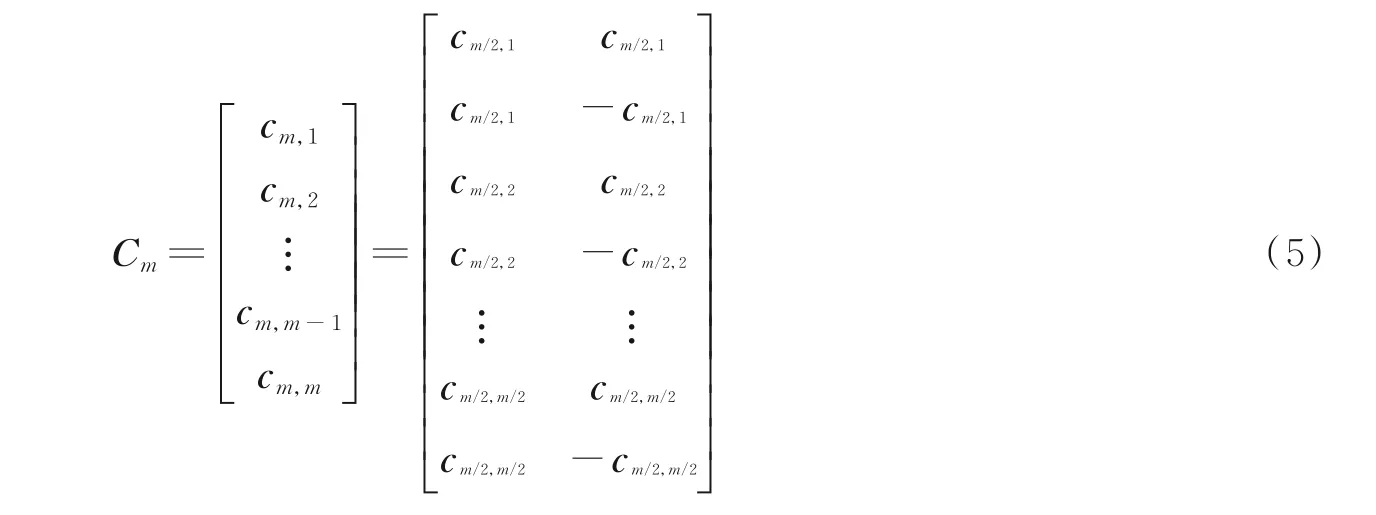
式中Cm的行向量cm，k为一个长度为m 的Walsh 序列，将cm，k用作信道化扩频码，将其定义为扩频因子为m 的OVSF 码。

不失一般性，假设发送信息序列为：a=[a1，a2，…，an]，a1，a2，…，an∈[±1±j]，信息序列a 采用OVSF 码集中c2，2=[c，-c]进行扩频，其扩频因子SF=2，扩频后的信息序列可表示为

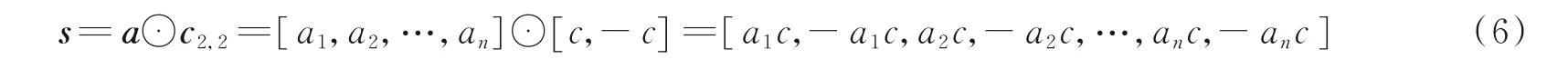
式中⊙表示Kronecker 积。

根据OVSF 码的继承关系可知该码的同阶兄弟码为（扩频因子SF=2）

与c2，1和c2，2相对应的子码分别为（扩频因子SF=4）

与c2，1和c2，2相对应的父码为（扩频因子SF=1）

本文分析均基于上述数学模型。

2 OVSF 码解扩模糊性分析

由于OVSF 码特有的继承关系，低阶码会在对应的高阶继承码数据段产生模糊性解扩结果，OVSF码解扩模糊性分析如下。不失一般性，假设c2，2是信息序列真实使用的扩频码，则c4，3，c4，4是它的子码，c2，1是 它 的 兄 弟 码，c1，1是 它的 父 码。根 据OVSF 码 的 性 质 可知，存 在 继 承 关 系 的 码 字 弱 正 交，即c1，1，c2，2，c4，3，c4，4存在 弱正交关系；没有继承关 系 的码字严 正 交，即：c2，1与c4，3，c4，4，c2，2满 足严正交关 系，c2，2与c4，1，c4，2，c2，1也满足严正交关系。

利 用 第2 阶 的 所 有 码c4，1，c4，2，c4，3，c4，4分 别 对 扩 频 信 息 序 列s 进 行 解 扩，解 扩 后 的 符 号 序 列 可 表示为

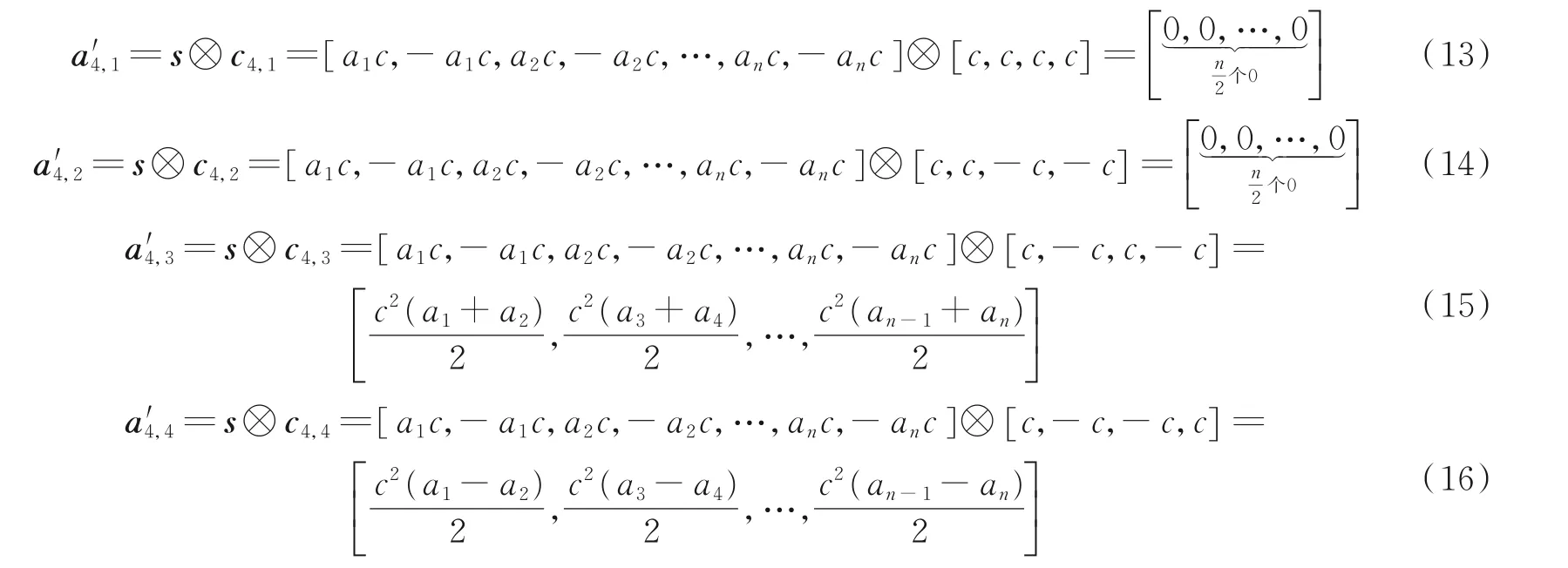
式中⊗表示解扩操作符。

解扩符号均峰值分别为

由式（19，20）可知，虽然信息序列中使用的扩频码是c2，2，但是当采用扩频码c4，3，c4，4进行解扩时出现了明显符号均峰值，产生了解扩模糊性，原因就在于c4，3，c4，4是c2，2的子码，由于c4，3，c4，4与c2，2存在继承关系，c4，3，c4，4与c2，2呈弱正交性，因此采用c4，3，c4，4进行解扩时，会出现符号均峰值，导致c4，3，c4，4与c2，2三个码的模糊性解扩结果。

利用第1 阶的OVSF 码c2，1和c2，2进行解 扩，解扩符号序列可表示为

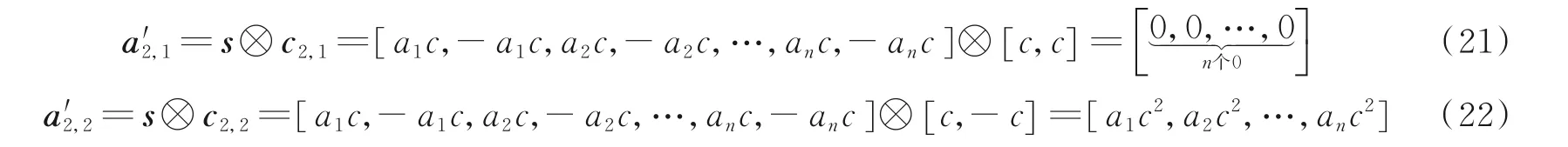
相应的符号均峰值计算为

由式（23）可知，由于c2，1和c2，2的正交，符号均峰值为0；由式（24）可知，由于信息序列采用的是扩频码c2，2进行扩频的，因此采用c2，2进行解扩时，出现了较大的符号均峰值。

利用第0 阶的OVSF 码c1，1进行解扩，解扩符号可表示为

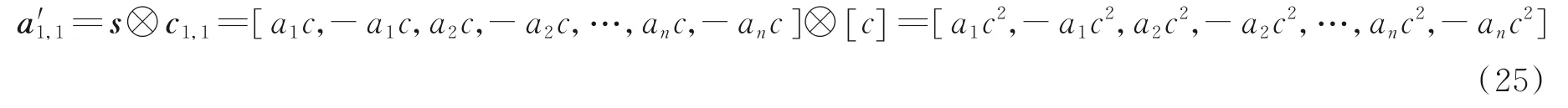
相应的符号均峰值为

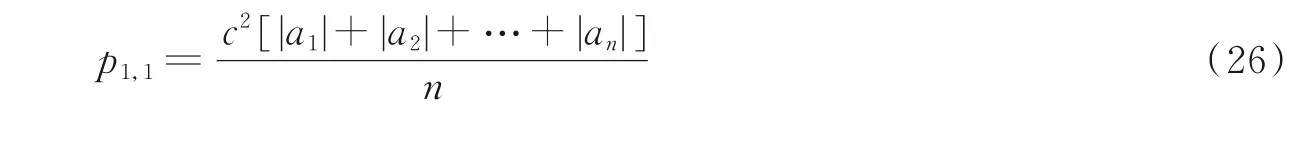
由式（26）可知，虽然信息序列中使用的扩频码是c2，2，但是当采用扩频码c1，1进行解扩时同样也出现 了 明 显 的 符号均峰值。原因就在于c1，1是c2，2的父码，由于c1，1与c2，2存 在 继 承 关系，c1，1与c2，2弱 正 交，因此采用c1，1进行信息序列解扩时会有较大的符号均峰值，继而导致c1，1和c2，2码的模糊性解扩结果。

上述分析结果表明，由于OVSF 码特有的继承关系，除了码c2，2具有明显的符号均峰值外，码c1，1，c4，3，c4，4也有较为明显的符号均峰值。由于存在继承关系的OVSF 码呈弱正交性，导致出现了解扩符号均峰值，继而引起了c1，1，c2，2，c4，3，c4，4解扩模糊性。因此，由于解扩结果的模糊性存在，无法确定哪些码才是信息序列s 真正的扩频码。同时可以看到，上述的分析只是假设只有1 个OVSF 码的情况，当同时存在多个OVSF 码时，情况更为复杂，解扩结果的模糊度更加严重，必须采用特殊的处理方法，消除OVSF 码之间的继承关系。

3 基于快速沃尔什-哈达玛变换的OVSF 码盲识别算法

3.1 基于快速沃尔什-哈达玛变换的信号解扩

沃尔什-哈达玛变换由于它只存在实数的加、减法运算而没有复数的乘法运算［18］，使得计算速度快、存储空间少，对实时处理和大量数据操作具有特殊吸引力。由Hadamard 矩阵的特性可知，沃尔什-哈达玛变换本质上是离散序列的各个元素按照一定的规律改变后进行加减运算，假设现有一个长度为N 的离散时间序列s(n)，其一维离散沃尔什-哈达玛变换定义为［19］

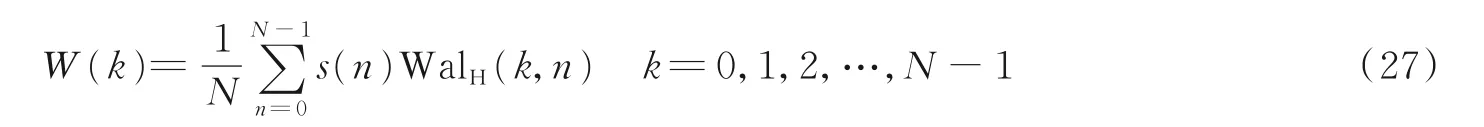
可将式（27）写成

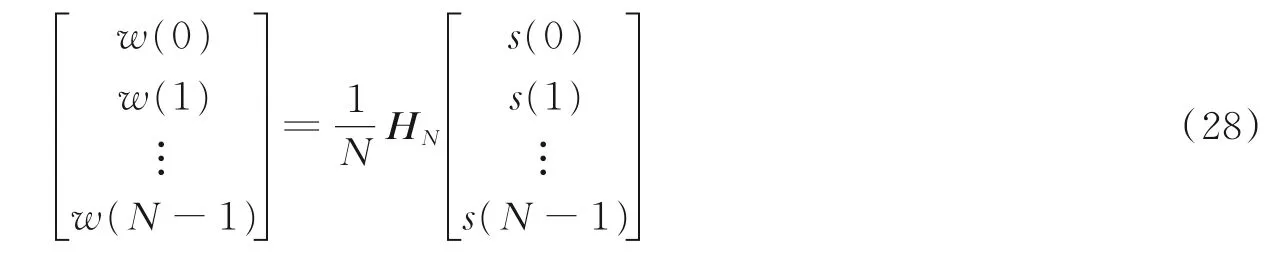
即

式中HN为N ×N 的Hadamard 矩阵，矩阵元素由+1 和-1 组成。

从式（29）可以看到，计算单点沃尔什-哈达码变换需要N -1 次加法，计算N 点沃尔什-哈达玛变换则共需要(N -1)×N ≈N2次加法。当序列长度增加时，其加法次数将以二次函数的方式增长，显然离散时间序列越长，计算速度越慢。如果离散时间序列s(n)的长度为512，按照式（29）需要做261 632 次加法。由于沃尔什-哈达玛变换可以采用类似FFT 算法中的蝶形结构来加快运算速度，从而实现快速沃尔什-哈达玛变换［19-20］。如果采用快速沃尔什-哈达码变换玛只需要N ×log2(N )次加减法运算。如果离散时间序列长度为512，采用快速沃尔什-哈达玛变换只需要做4 608 次加法，运算速度可提升50 多倍。

对于某一指定的扩频因子，其相应的OVSF 码集实际上是一个Hadamard 矩阵。假设数据表示成s=[s0，s1，…，sN-1]，将序列s 变换成SF×K 数据矩阵，如式（30）所示。

采用OVSF 码集对数据矩阵S 进行解扩，获得的符号矩阵是一个SF×K 的矩阵，如式（31）所示。

因此解扩计算方法可以表示为

由于OVSF 码集就是一个Hadamard 矩阵，即HSF=CSF，所以式（33）可以写成

观察式（33）可以发现，采用OVSF 码集对数据矩阵S 进行解扩，实际上是对其进行沃尔什-哈达玛变换，解扩一个符号需要做(SF-1)×SF 加法，解扩K 个符号需要做(SF-1)×SF×K=(SF-1)×N 次加法。采用沃尔什-哈达玛变换进行解扩时仍需要大量的加法运算，由于沃尔什-哈达玛变换有基于蝶形结构的快速沃尔什-哈达玛变换，采用快速沃尔什-哈达玛变换解扩K 个符号所需要的加法次数为SF×log2(SF)×K=log2(SF)×N 次，很明显，快速算法的运算量可提升倍。

3.2 OVSF 码盲识别算法实现

WCDMA 下行链路业务信道OVSF 码的扩频因子SF 的使用范围是4～512［1-2］，因此OVSF 码的识别从扩频因子SF=512 开始，直到扩频因子SF=4 结束。算法思想是：首先剔除c256，1和c256，2两个已知公共信道的扩频码［1-2］以及与其存在继承关系的所有码字并建立备选码字集。算法从最高阶OVSF 码开始逐步进行到最低阶，即顺序为SF=210-k，k=1，2，…，8。对于每个扩频因子SF=210-k，k=1，2，…，8 及相应的备选码字集执行下列步骤：首先按照上述顺序，利用相应的备选扩频码对循环移位前后的扩频信息序列进行解扩并计算符号均峰值；然后计算符号均峰值差，其目的是消除所有低阶与其存在继承关系码字的影响。最后对上述的差值进行检测。如果检测到峰值并且超过阈值门限，提取峰值对应的扩频码，同时进行备选码字集的更新，在备选码字中剔除所有与该码存在继承关系的所有低阶码字。如果检测到的均峰值低于阈值门限，认为该信息序列没有使用本阶OVSF 码，则不进行备选码字的更新。按照上述方法从高阶码字开始逐步执行到最低阶码字为止，算法实现流程如下。

输入数据s=[s1，s2，…，sN]

输出扩频因子SF 以及相应的扩频码cSF，n

初始化建立OVSF 码备选集C，通过已知广播信道扩频码c256，2，计算广播数据循环移位前后解扩符号均峰值并计算符号均峰值差继而确定阈值门限Thr=Δp256，2×μ（考虑噪声影响，引入抖动因子μ）。

（1）k=1，SF=210-k

（3）计算符号均峰值

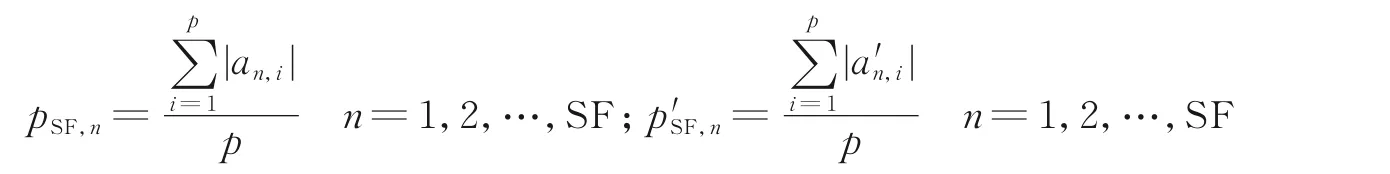
（4）计算符号均峰值差

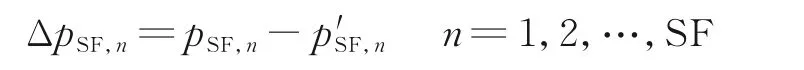
（5）判决

如果ΔpSF，n＞Thr，找到超过门限对应的扩频码cSF，n′，计算跟cSF，n′有继承关系的所有低阶码字，同时更新OVSF 码备选集C；如果ΔpSF，n＜Thr，不更新OVSF 码备选集C。

（6）如果SF ＞4，k=k+1，跳转到步骤（1）；如果SF=4，算法执行结束。

根据实际工程需要，算法必须具有实时处理能力，但从上述处理流程看出，该算法中需要进行大量的解扩计算，要求在30 ms 内完成OVSF 码的识别，无法满足工程上实时处理要求，必须进一步降低算法计算量。研究中发现，OVSF 码识别算法中计算量最高的是要频繁地进行信号解扩运算。3.1节指出，采用快速沃尔什-哈达玛变换实现信号的解扩可大量降低信号解扩计算量，因此上述算法流程中对循环移位前后数据s 和s′进行解扩计算时均采用快速沃尔什-哈达玛变换实现，具体实现方法总结如下。

输入数据s=[s0，s1，…，sN-1]

输出解扩符号矩阵

（2）对数据矩阵S 进行快速沃尔什-哈达玛变换

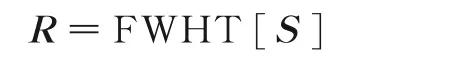
（3）矩阵R即为OVSF码集解扩结果，将解扩结果代入OVSF码盲识别算法中的步骤（1）和（2）。

4 性能分析

第2 节证明了OVSF 码存在解扩模糊性，为了消除这种模糊性，必须对发送的扩频信息序列进行变换处理，构造新扩频信息序列，使其变换后的新扩频信息序列不改变当前码对应的所有低阶父码的信息。根据OVSF 码的递归构造原理可知，OVSF 码扩频因子为SF=2k，k=0，1，2，…，因此将扩频信息序列循环移位SF/2 后，对于扩频因子为SF/2k，k=1，2，…的OVSF 码而言，循环移位前后的扩频信息序列中包含的这些OVSF 码的信息没有变化，因此当采用扩频因子SF 的OVSF 码对循环移位前后的扩频信息序列进行解扩后，得到的符号均峰值包含的所有扩频因子为SF/2k，k=1，2，…的OVSF 码的信息一样，于是可以对循环移位前后解扩后的符号均峰值求差的方法，消除所有扩频因子为SF/2k，k=1，2，…的OVSF 码对扩频因子为SF 的OVSF 码的影响。具体分析证明如下。

不失一般性，从第2 阶（扩频因子SF=4）开始OVSF 码的识别，首先采用码集c4，1，c4，2，c4，3，c4，4对扩频信息序列s 进行解扩，获得解扩符号均峰值p4，1，p4，2，p4，3，p4，4（如式（17～20）所示）。然后将扩频信息序列进行变换，即对扩频信息序列s 循环移位个码片，循环移位后的序列如式（34）所示。

再利用码c4，1，c4，2，c4，3，c4，4对循环移位后的扩频序列s′进行解扩，解扩后的符号序列如式（35～38）所示。

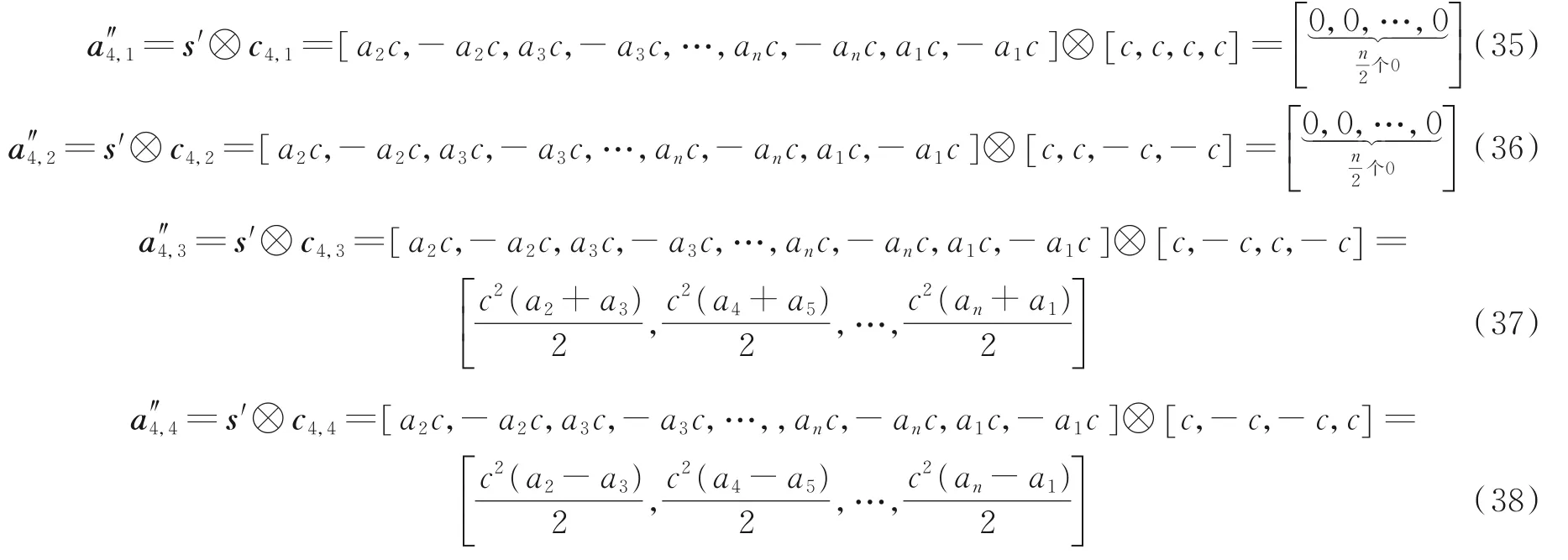
相应的符号均峰值如式（39～42）所示。

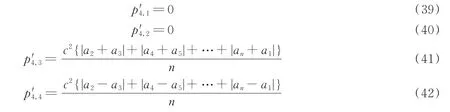
对扩频信息序列循环移位前后解扩的符号均峰值求差的结果如式（43～46）所示。

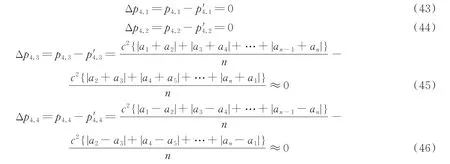
式（43～46）表明，当采用高阶子码对循环移位前后的扩频信息序列进行解扩后，得到符号均峰值相对于所有低阶父码在统计上相等。所以采用对扩频信息序列循环移位前后的解扩符号均峰值求差的方法可以消除所有低阶父码对高阶子码的影响，继而消除因继承关系导致的扩频码模糊性不可识别。因此可以判断，该发送信息序列中不存在扩频因子SF=2 的OVSF 码。因为假若存在，消除所有低阶OVSF 码后，由于扩频增益，一定在相应的扩频码位置出现较大的符号均峰值。

第2 阶的OVSF 码识别完毕后，再进行下一阶码的识别，即进行第1 阶扩频因子SF=2 的OVSF 码的识别。将扩频信息序列s 循环移位SF/2=1 个码片，循环移位后的扩频序列如式（47）所示。

利用扩频码c2，1，c2，2分别对循环移位后的扩频序列s′′进行解扩，解扩后的符号序列如式（48～49）所示。

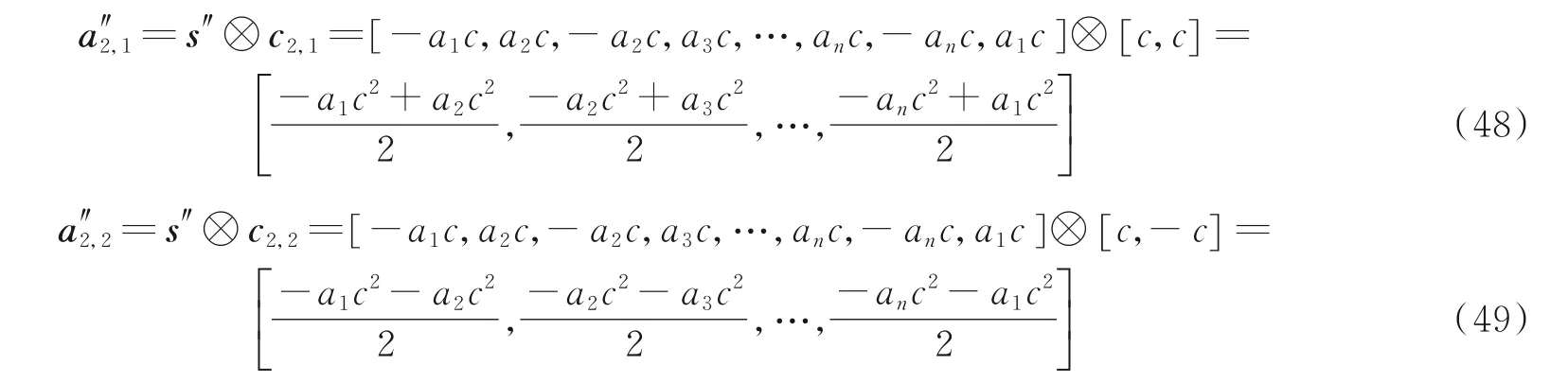
c2，1，c2，2解扩符号均峰值如式（50～51）所示。

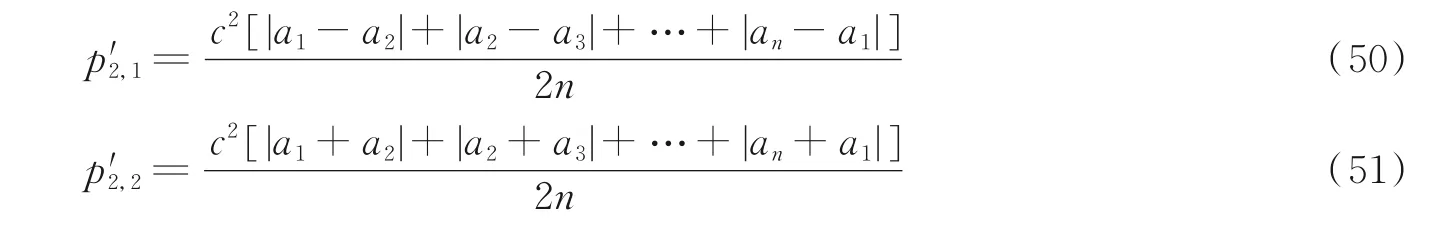
由于对原始扩频信息序列进行了SF/2=1 个码片的循环移位，当采用c2，1对循环移位数据进行解扩时，由于c2，1不再与循环移位后的扩频信息序列正交，因此产生了符号均峰值（如式（50）所示）。当采用c2，2对循环移位数据进行解扩时，同样产生解扩符号均峰值（如式（51）所示），但此时的解扩符号均峰值要小于循环移位前的解扩符号均峰值，证明如下。

采用c2，2对循环移位前的信息序列进行解扩，解扩符号均峰值如式（24）所示，重写如下

于是有

采用c2，1，c2，2对扩频信息序列循环移位前后进行解扩的符号均峰值差可以表示为

显而易见，由于|a1|+|a2|＞|a1+a2|，|a2|+|a3|＞|a2+a3|，…，|an|+|a1|＞|an+a1|，所 以 式（56）Δp2，2＞0 即Δp2，1＜0，Δp2，2＞0。由于Δp2，1＜0，Δp2，2＞0，此时通过扩频信息序列循环移位前后解扩的符号均峰值求差结果可判断发送信息使用的扩频为c2，2。由于已经确定了c2，2是发送扩频信息序列的扩频码，根据OVSF 码的分配原则可知［7-9］，系统不会再将扩频码c1，1分配给其他业务信道，可以将c1，1从备选OVSF 码集中剔除。

上述分析表明，采用本文算法对数据进行循环移位后再进行解扩可消除因OVSF 码的继承关系引起的解扩模糊性，可唯一确定信道中的OVSF 码，提高了识别成功概率。

5 计算复杂度分析

实际工程应用中，要求算法用30 ms 完成3 帧数据内所有OVSF 码的识别工作，以下针对3 帧数据进行计算复杂度分析。

常规算法所需要的复数乘法

常规算法所需要的复数加法

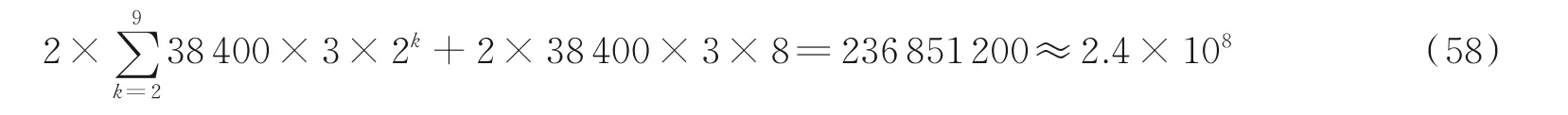
采用快速沃尔什-哈达玛变换所需要的加法

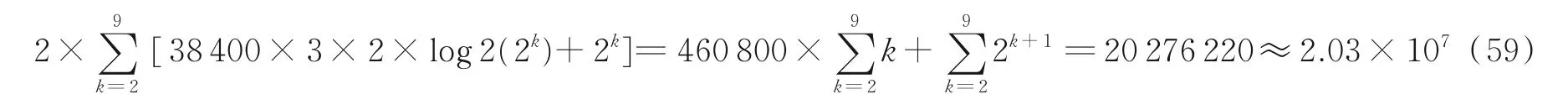
CPU 计算加减法大约需要3 个时钟周期，乘法的速度比加减法慢近10 倍，除法的速度比加减法慢20 倍左右。就目前主流CPU 运算能力而言，一次浮点加法运算需要1 个CPU 时钟周期即可完成，一次乘法运算大约需要2 个CPU 时钟周期。以单核CPU 2.5 GHz 主频为例，时钟周期为0.4×10-9s，因此一次加法运算需要的时间大约0.4×10-9s；一次乘法运算需要的时间大约0.8×10-9s。由于OVSF 码识别算法所需复数乘法次数为2.4×108次，换算为实数乘法次数大约为4.8×108次，因此采用常规算法需要总的乘法运算时间为tmultiple=0.384 s；需要总的加法运算时间为tadd=0.096 s，因此算法所需总的运算时间大约为：tadd+tmultiple=0.48 s=480 ms，运算时间无法满足工程需求。

采用快速沃尔什-哈达玛变换进行解扩运算时，OVSF 码识别算法只有加法运算，没有乘法运算，算法所需要的加法次数为2.03×107次，因此采用快速沃尔什-哈达玛变换进行解扩运算时，OVSF 码识别算法所需总的运算时间为tadd=0.008 2 s=8.2 ms。通过上面的分析，在计算机主频为2.5 GHz、单核CPU 的条件下，若采用常规方法约需要480 ms 才能完成3 帧数据的OVSF 码识别；若采用快速沃尔什-哈达玛变换方法仅需8.2 ms 即可完成3 帧数据的OVSF 码识别，满足工程上实时处理要求。

6 仿真实验

实验1考察在不同信道功率条件下算法性能

本次实验主要考察在不同信道功率条件下算法性能，同时与文献［17］算法进行对比。算法性能评价指标为OVSF 码成功识别概率，其定义为：OVSF 码识别成功率p=正确识别每个OVSF 码的实验次数/实验的总次数，仿真实验的总次数为1 000。具体仿真参数设置如表1 所示。

表1 实验1 参数设置Table 1 Parameter setting of experiment 1

实验结果如图1 所示，图1 给出了信道功率在-25～-10 dB 时，3 个OVSF 码成功识别概率。从实验结果可以看到，当信道功率为-14 dB 时，本文算法对3 个OVSF 码的成功识别概率均在95%以上；当信道功率增加到-10 dB 时，文献［17］算法与本文算法性能相当。在低信噪比情况下，本文算法表现更优越，主要原因是本文算法在采用快速沃尔什-哈达码变换进行解扩时，获得了部分扩频增益，因此数据循环移位前后解扩的符号均峰值体现更为明显，识别准确度就越高，而文献［17］算法没有利用OVSF 码的扩频增益，因此在低信噪比的情况下识别成功概率较低。

还可以发现，由于本文算法对信号实施了解扩运算，扩频因子较大的OVSF 码比扩频因子较小的OVSF 码能获得更大的扩频增益，因此本文算法对扩频因子为128 的OVSF 码识别成功概率要比扩频因子为64 和32 的OVSF 码识别成功概率高。然而文献［17］算法却出现了恰好相反的结果，扩频因子为32 的OVSF 码识别成功概率要比扩频因子为64 和128 的OVSF 码识别成功概率略高，其原因是文献［17］算法没有解扩的过程，无法获取扩频增益。识别成功概率完全取决于信号本身功率和所使用的数据内的码周期数，信噪比越高，数据内包含的码周期越多，相关矩阵累加平均估计越准确。对其进行奇异值分解时，奇异值区分度大，识别准确率高，因此对于同样长度的信息序列和相同信噪比情况下，由于扩频因子较小的OVSF 码包含的码周期多，相关矩阵累加平均估计越准确，码的识别概率越高。

实验2考察信道中存在多个OVSF 码时，算法同时识别性能

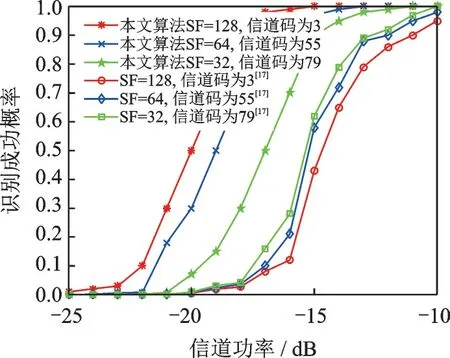
图1 不同信道功率情况下OVSF 码成功识别概率Fig.1 Recognition probability for OVSF code under different channel powers

WCDMA 移动通信系统除支持话音业务以外，还支持其他多种数据业务，均需要OVSF 扩频码通过可变数据速率得以实现。因此某一信道中可能同时使用多个VOSF 扩频码，对于非合作情况，算法对多个OVSF 码的同时识别意义很大，因此本次实验重点考察算法对OVSF 码同时识别性能。同时与文献［17］算法进行对比，在1 次仿真实验中，当所有的OVSF 码被同时正确识别时，则认为本次实验成功，OVSF 码数量从1 增加到30，具体实验参数设置如表2 所示。

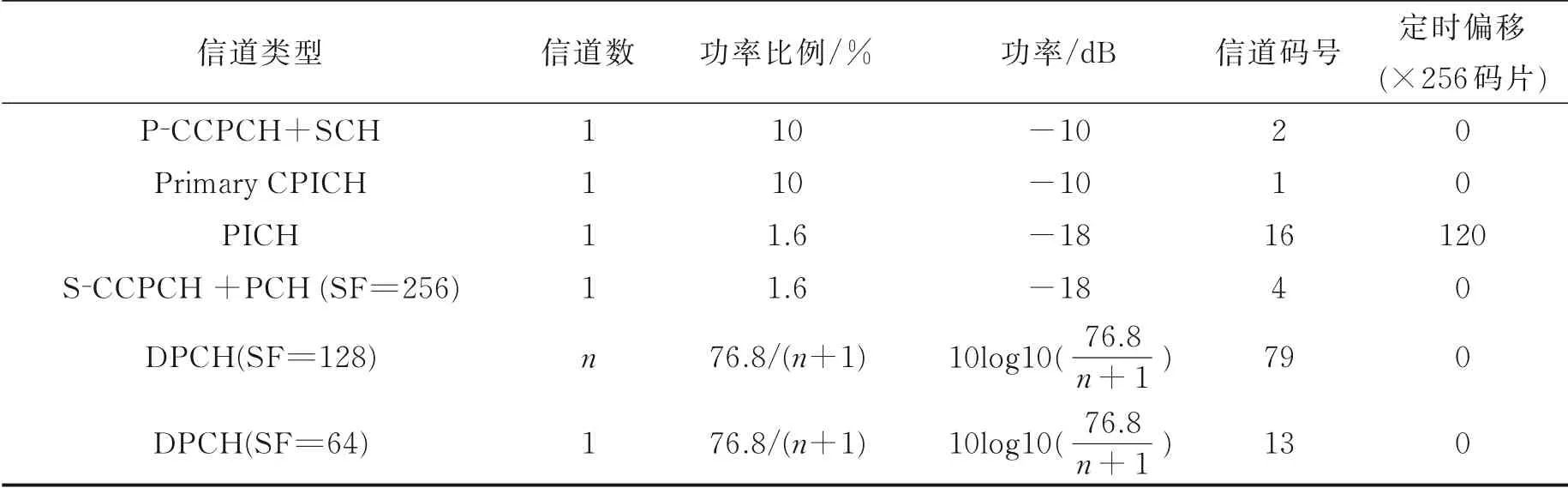
表2 实验2 参数设置Table 2 Parameter setting of experiment 2

实验结果如图2 所示，图2 中给出了成功识别概率随OVSF 码数量变化的关系。

从仿真结果可以看到，本文算法同时识别23 个OVSF 码的成功概率约为95%，随着OVSF 码数量的增加，性能开始呈下降趋势，主要原因是OVSF 码数量越多，多址干扰愈加严重。当干扰超过扩频增益后，性能开始下降，当OVSF 码数量达到30 个时，成功识别概率降为60%左右。由于文献［17］算法只考虑了单用户情况，只能对信道中的单个OVSF 码进行识别，当存在2 个以上OVSF 扩频码时性能严重恶化，因此文献［17］算法不适合多个OVSF 码同时识别的情况。

实验3考察算法计算复杂度

实验环境采用的计算机主频为2.5 GHz、单核CPU，以CPU 处理时间作为评价标准，与文献［17］算法进行对比，信道中OVSF 码的数量从1 增加到30，其他参数设置同实验2。实验结果如图3 所示，图3中给出了CPU 处理时间随OVSF 码数量变化的关系。

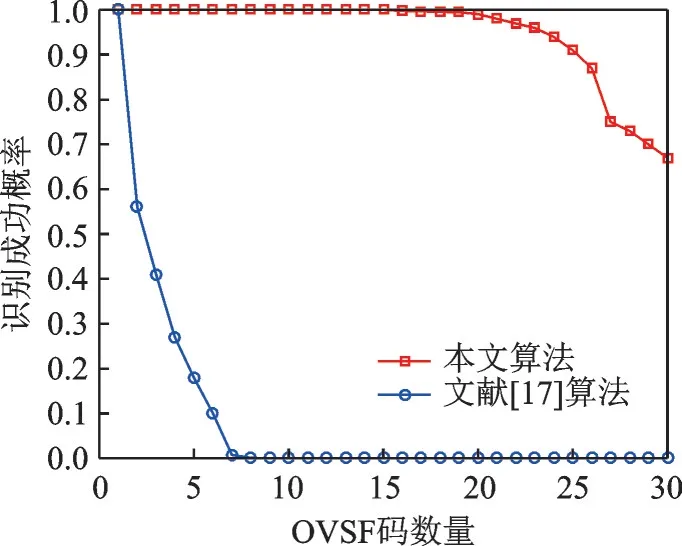
图2 不同OVSF 码数量情况下成功识别概率Fig.2 Recognition probability for OVSF code with different numbers of OVSF code

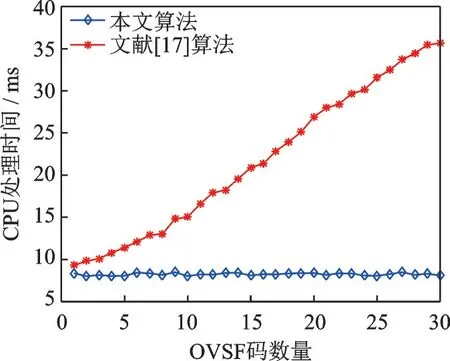
图3 不同OVSF 码数量情况下CPU 处理时间Fig.3 CPU processing time with different numbers of OVSF code

从仿真结果可以看到，随着OVSF 码数量不断增加，文献［17］算法CPU 处理时间呈线性增长趋势，而本文算法CPU 处理时间始终保持在8.2 ms 左右。主要原因是文献［17］算法在进行1 个OVSF 码识别时就要进行200～400 次左右的相关矩阵累加平均和1 次奇异值分解计算，OVSF 码数量越多，相关矩阵累加平均和奇异值分解次数越多，计算量越大，CPU 处理时间越长。而本文算法只需要1 次快速沃尔什-哈达玛变换就可完成所有数据的解扩计算，与OVSF 码数量无关，而且算法中快速沃尔什-哈达玛变换只涉及加法运算，不涉及乘法运算，计算量小，CPU 处理时间相对而言较少，而且计算量基本保持不变。

实验4考察阈值门限对算法性能的影响

考虑到噪声影响，算法在具体实现过程中，判决阈值门限引入了抖动因子μ，其取值范围应该根据噪声情况进行合理选择。本次实验重点考察抖动因子μ 对算法性能的影响，从而为抖动因子μ 的选择提供依据。具体仿真参数设置如表3 所示。在1 次仿真实验中，当所有的OVSF 码正确识别时，则认为本次实验成功，具体实验参数设置如表3 所示。

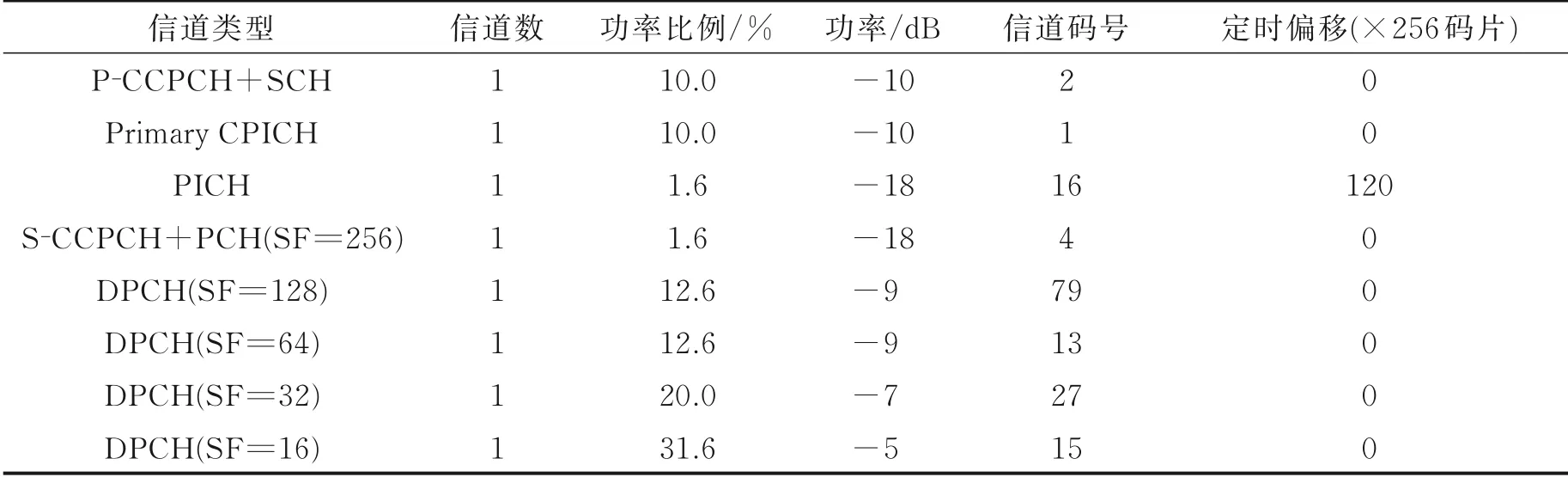
表3 实验4 参数设置Table 3 Parameter setting of experiment 4

实验结果如图4 所示，图4 中给出了识别概率随抖动因子μ 变化的关系。

从仿真结果可以看出，当μ ∈[0.6，0.9]时，信道中多个OVSF 码同时识别正确率接近100%，μ取其他值时，OVSF 码同时成功识别概率较低。主要原因是当μ ∈[0，0.5]时会导致错检；当μ ＞0.9时会导致漏检。在实际工程应用中，μ ∈[0.6，0.9]可以作为一个经验值使用。值得注意的是，由于公共广播信道是已知公开的信息，并且扩频码固定为c256，2，因此可以以广播信道接收功率作为参考信号来计算符号均峰值差，然后在算法初始化时，采用Thr=Δp256，2×μ 确定阈值门限。

图4 不同抖动因子μ 情况下OVSF 码成功识别概率Fig.4 Recognition probability for OVSF code with different values of μ

7 结束语

本文对OVSF 码的递归构造方法、码树结构模型、数学理论基础以及分配原则进行了深入研究。在此基础上，针对第3 方非合作接收情况，利用OVSF 码不同阶之间的继承关系和正交特性，结合快速沃尔什-哈达玛变换，提出了一种快速OVSF 码盲识别算法。该方法能在非合作和无任何先验知识以及低信噪比情况下，实现了对WCDMA 系统下行业务信道中的多个OVSF 码进行同时盲识别。该方法具有较低的计算复杂度，满足工程应用中实时处理要求，实测中8.2 ms 可完成3 帧数据内20 个OVSF 扩频码的同时识别，识别准确率在95%以上。另外，本文算法还为WCDMA 信号快速盲解扩奠定了基础，在对WCDMA 信号侦察方面具有重要意义。