理想流体的Laplace方程有限元解法
2021-02-04郭元辉
陈 瑶,郭元辉
(1.西华师范大学数学与信息学院,四川南充 637009;2.西华师范大学教育信息技术中心,四川南充 637009)
0 引言
在大自然现象中,科学的研究,往往借助于各种复杂的偏微分方程的描述.拉普拉斯方程是最常见的一种,它广泛应用于流体力学、弹性力学、热传导,电磁波、现代光学等.它的基本形式为[1,2]
Δφ=0.
(1)
如何求解偏微分方程是现代科学计算所研究的一个主要问题.科学计算与实验、理论已并列成为现代科学研究的三种方法.科学计算不仅是一种数字计算的手段,而且也是一种研究方法[3].从早期的古典解、解析解,到近代的数值解、近似解,有限差分、有限元[4-6]、边界元及深度学习、人工智能算法等,各种方法不断出现、创新,带来计算科学和技术的发展,以及更高的数值精度和数学理论、科学理论的进步.
1 问题及方程

图1 示意图Fig.1 The diagram
假设在图1所示的两个平行平板间,通入速度为2 m/s的空气,出口敞开.平行平板的长度为10 m,宽度为5 m.试求流动区域内的速度式分布[7].
理想流体[8]通常定义为其内部没有摩擦的流体,称为无黏性流体.这里,假设空气满足理想流体的基本特性,也就是黏滞系数η为0;同时,不可压缩,密度ρ为常数[9,10].那么,理想流体的连续性方程为
(2)
其中,u,v分别表示速度势函数φ(x,y)在x,y方向的导数∂φ/∂x,∂φ/∂y,代入式(2)得到
(3)
这就是Laplace方程形式.本题中有两类边界条件.
第一类边界,也叫Dirichlet边界条件,在边界上知道速度势φ(x,y)的值.第二类边界,又叫Neumann边界条件,知道边界上速度势的法向导数∂φ/∂n.
2 有限元理论
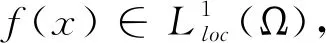

定义1.2对于非负整数k和实数p≥1,定义
Wk,p(Ω)={u∈Lp(Ω):∂∂u∈Lp(Ω),∀|α|k}.
这是一个Banach空间.赋予范数


设f⊂L2(Ω),这里考虑更一般的Poisson方程,本题Laplace方程仅仅是f=0的特例.
(4)
设u∈H2是方程(4)的古典解,定义空间V:={v∈H1(Ω):v|Γ=0},



(5)
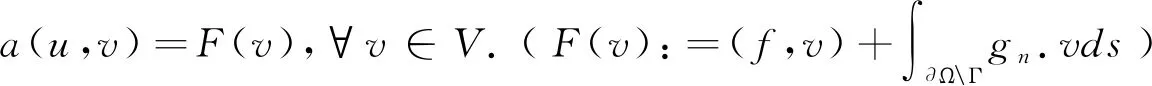
(6)
这样求出的弱解与古典解具有等价性[4].v所在的空间,称为试验空间;u所在的空间成为容许空间.当使用Galerkin方法时,两者取同一空间,称为能量空间.
那么,如何保证弱解的存在唯一性?
定理1.1[5](Lax-Milgram Lemma)假设V是一个Hilbert空间,定义范数‖ . ‖和内积(. , .),a(. , .)是映射V×V→R上的双线性函数,存在常数α,β>0满足
连续性|a(u,v)|β‖u‖‖v‖,∀u,v∈V,
(7)
和V-椭圆a(v,v)≥α‖v‖2,∀v∈V.
(8)
那么,存在唯一的解u∈V,满足a(u,v)=F(v),∀v∈V.
定理的证明用能量范数和Ritz表现定理可以得到,此处不加证明地引用.
定义1.3有限元是一个具有如下性质的三元组(K,P,N)
i.K∈d是一个具有分片光滑边界的闭集;
ii.P是K上的有限维函数空间;
iii.N={N1,...,Nn}是一组由节点P'构成的基.

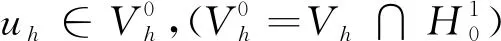
(9)

‖u-uh‖L2(Ω)Ch2|u|H2(Ω).
证明:i. 对任意g∈L2(Ω),问题
(10)

ii.存在常数C满足
‖φg‖H2(Ω)C‖g‖L2(Ω).
(11)
iii.取g=u-uh,让φg是方程(9)的解,那么
=(u-uh,g)
=a(u-uh,φg)
=a(u-uh,φg-Ihφg)
证毕.
3 程序设计方法
根据有限元理论,通过程序设计实现Laplace方程的计算,这里有几个主要步骤.
i.区域的剖分.通常区域可以使用三角形剖分或四边形剖分,这里根据题目条件,选择四边形剖分,给出若干行列,把区域划分成大小相等的小四边形.标记上节点和单元编号.
ii.选择基函数.因为对每一个单元,只需要用到四个节点的函数值,所以插值函数用双线性形式:
φ(x,y)=ax+by+cxy+d.

for k=1:dys
dybh=dyjd(k,:); dyzb=jdzb(dybh,:);
xc=sum(dyzb(:,1))/4;yc=sum(dyzb(:,2))/4;
b=(dyzb(2,1)-dyzb(1,1))/2;c=(dyzb(4,2)-dyzb(1,2))/2;
ke(1,1)=(b^2+c^2)/(3*b*c);ke(1,2)=(b^2-2*c^2)/(6*b*c);
ke(1,3)=-(b^2+c^2)/(6*b*c);ke(1,4)=(c^2-2*b^2)/(6*b*c);
ke(2,1)=ke(1,2);ke(2,2)=ke(1,1);ke(2,3)=ke(1,4);ke(2,4)=ke(1,3);
ke(3,1)=ke(1,3);ke(3,2)=ke(2,3);ke(3,3)=ke(1,1);ke(3,4)=ke(1,2);
ke(4,1)=ke(1,4);ke(4,2)=ke(2,4);ke(4,3)=ke(3,4);ke(4,4)=ke(1,1);
kk(dybh,dybh)=kk(dybh,dybh)+ke; % 总装
end

v.计算结果.u=A-1B.
通过Matlab编程,计算结果如表1所示.
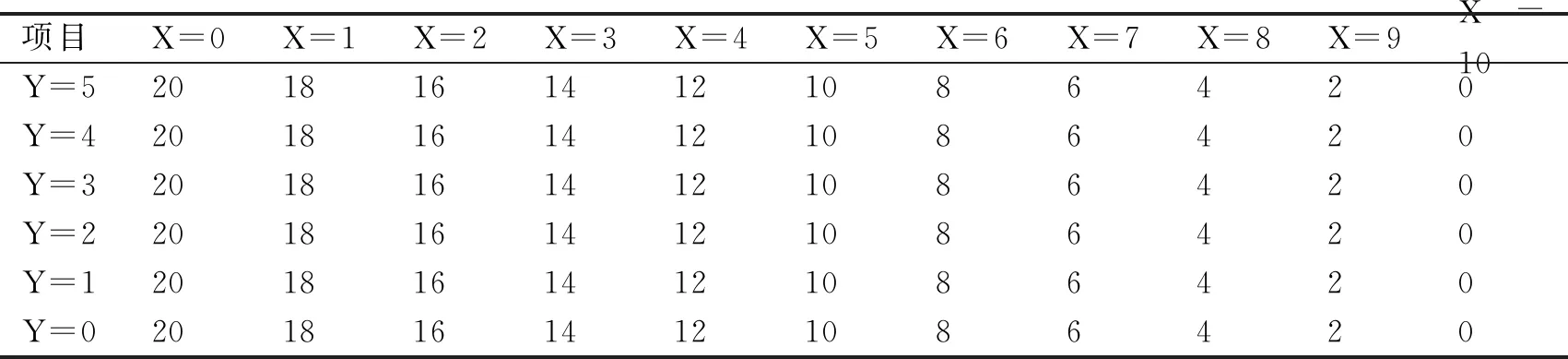
表1 区域剖分为5×10个四边形时,节点所对应的uTab.1 u corresponding to the node when the region is divided into50quadrilaterals
4 使用PDE-Tool与freeFem++计算
在MATLAB中,利用偏微分方程工具PDE-Tool,直接代入方程参数与边界条件[13],可以得到与表-1一样的结果,如图2所示.
同样,为了验证计算的结果,这里也可以使用网上的免费软件Freefem++[14],它是一个高度集成化的有限元软件,其编程简单、直观、高效,其核心部分的书写与变分形式一一对应,并且把第一边界、第二边界的处理也封装了.例如:
problem laplace(u,v)=int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v))
-int2d(Th)(Fh*v)
+on(2,u=0)
-int1d(Th,1)(0*v)-int1d(Th,3)(0*v)
-int1d(Th,4)(2*v);
使用Freefem++的计算结果如图3所示.

图2 PDE-Tool效果图Fig.2 Calculation effect of PDE tool图3 Freefem++计算效果图Fig.3 Freefem++ calculation effect picture
