能谱定量分析的不确定度评估

刘 英 张勋高

(武汉大学测试中心，武汉 430072)

能谱(Energy Dispersive Spectroscopy，EDS)分析是一种通过能量色散并用半导体探测器探测特征X射线能量及强度实现元素的定性和定量分析技术。由于样品发射的X射线直接进入探测器，且探测器与样品之间的距离短，相对于X射线波谱分析(WDS)，EDS具有更高的探测效率[1]，激发电流通常可以降低1个数量级，对样品近乎无损分析。与扫描电子显微镜(SEM)或透射电子显微镜(TEM)结合，EDS已成为微区原位主成分的定性和定量分析的重要手段。随着电制冷技术、新型高透过窗口或无窗探测器的推广以及软件的不断完善，EDS技术日趋完善，元素分析范围可涵盖4B～92U，检测灵敏度达到0.1%甚至更低，同时由于仪器结构简单、价格较低、使用方便等优势，近年来EDS几乎是新购置SEM、TEM仪器必备附件之一，在科学研究和产品生产、研发领域应用十分普及[2-5]。目前，EDS的使用以元素的定性、面、线分布以及无标样半定量分析为主，而在微区的准确定量分析方面仍面临很大挑战，主要原因在于影响EDS定量分析的因素众多，定量结果的准确性不仅与样品的导电性、平整度、致密性和均匀性有关，同时也与分析过程中能谱仪定量分析参数的控制关系密切[6,7]。相比较而言，对后者探究甚少，更容易被忽视。

测量结果不确定度是判断检测方法和测量结果是否可靠的重要指标[8]。通过不确定度的评估，有助于深入了解影响实验结果正确性的因素和对分析过程的合理控制[9]。近年来，为了满足相关国际标准及国际组织的互认要求，认可认证实验室均需要对检测和校准项目进行不确定度评估[10]。目前，王宇等[11]对EDS无标样半定量分析结果的不确定度进行了评估，但有关EDS定量分析不确定度却知之甚少。本研究详细分析EDS定量分析过程中不确定度的来源，探讨能谱参数对结果的影响，对定量分析的不确定度进行了评估，为EDS定量分析的质量控制及该类仪器测量不确定度评定提供借鉴。

1 实验部分

1.1 仪器

利用场发射电子探针显微分析仪(EPMA，JXA-8530F Plus，JEOL Co. ltd.，Japan) 配置的电制冷型能谱仪(ELECT SUPER,70 mm2, EDAX Inc. USA)进行EDS数据的采集，样品激发电压设定为20 kV，时间常数3.84或7.68，死时间控制在20%～40%之间，单次测量信号收集时间100 s，EDS峰和背景信号由EDAX TEAM软件自动读取，EDS能量分辨率Mn Kα 125 eV左右。样品的激发电流通过EPMA的探针电流检测器(PCD)读取。

1.2 样品

实验样品为钛非晶合金薄膜(主要组成为Zr, Ti, Ni和Cu)，厚度约150m，薄膜的两面分别为光面(A)和亚光面(B)(如图1所示)。样品有良好导电性和稳定性，(A)表面元素分布均匀，用于研究分析线强度的影响因素；作为对比，(B)表面用于研究样品的不均匀和不平整性对分析结果的影响。

图1 样品的光面(A)和亚光面(B)背散射图像

定量分析所用标准样品为电子探针标样(中国科学院地质与地球物理研究所)，其中分析Zr、Ti、Ni和O元素所用的标样分别为GSB 01-1791-2004 ZrO2(75.23%0.14%)、GSB 04-1416-2001 TiO2(99.960.10%)、GSB A70039-89 NiO (99.95%0.15%)和GSB A70013-86 Al2O3(99.990.18% )，Cu和Si元素所用的标样分别为纯元素标样，其含量分别为99.99%和99.9%。

1.3 EDS定量分析的测量模型

EDS定量方法：在相同激发电压下，通过对样品和标准样品的元素分析线单位电流净强度比较，获得强度因子k，再用软件提供的ZAF因子校正从而获得待测元素的含量。

能谱定量分析的测量模型为：

(1)

式中，强度因子k为样品和标准样品中待测元素分析线单位电流净强度之比；

w为样品的元素含量测量值；

w0为标准样品的元素含量标称值；

I和I0分别为样品和标准样品中待测元素分析线净强度测定值；

i和i0分别为样品和标准样品的激发电流，其大小通过扫描电镜配置的法拉第杯进行测定，本实验激发电流大小通过EPMA的PCD读取；

Z、A、F分别是基体原子序数、吸收效应和荧光效应校正因子，待测元素的ZAF大小由仪器软件依据测量对象的元素组成通过迭代计算后给出[12]；

由(1)式可知，测量值w的不确定度由I、I0、i0、i、Z、A、F和w0输入量的不确定度决定。假设输入变量I、I0、i0、i、Z、A、F和w0之间不相关，且由于I和I0的测量是在相同的工作条件下进行，影响分析线强度的因素相同，可以将这两个分量合并为2倍的I分量，i和i0分量的影响因素相同，二者合并为2倍的i分量。根据不确定度传播律[13]，测量结果的相对合成方差

(2)

(2)式中各输入变量的灵敏系数均为1，则测量结果的相对合成不确定度

(3)

(3)式中urel(I)、urel(i)、urel(Z)、urel(A)、urel(F)和urel(w0)分别为各分量的相对标准不确定度。

1.4 测量不确定度来源与识别

(1)分析线强度引起的测量不确定度来源包括随机因素、激发电流的大小、工作距离(WD)、电子束焦距、取样点大小等分量；

(2)电流示值可读数和稳定性引起的测量不确定度；

(3)ZAF因子引起的测量不确定度；

(4)标准样品的示值不确定度引起的测量不确定度。

2 结果与讨论

2.1 分析线强度引起的测量不确定度

2.1.1随机因素引起的分析线强度测量的不确定度

在电压20 kV，电流1.00 nA，WD为11.0 mm，在样品A面同一点连续进行11次分析。Zr Lα，Ti Kα，Ni Kα和Cu Kα的强度以及4种元素的ZAF校正因子测量结果如表1所示。

由表1可以看出，与强度测量的相对标准偏差相比较，各元素的ZAF校正因子测量的相对标准偏差要小1～2数量级，说明由ZAF校正因子引起的不确定度为非主要因素。

表1 样品中元素分析线强度和ZAF校正因子连续11次测量结果

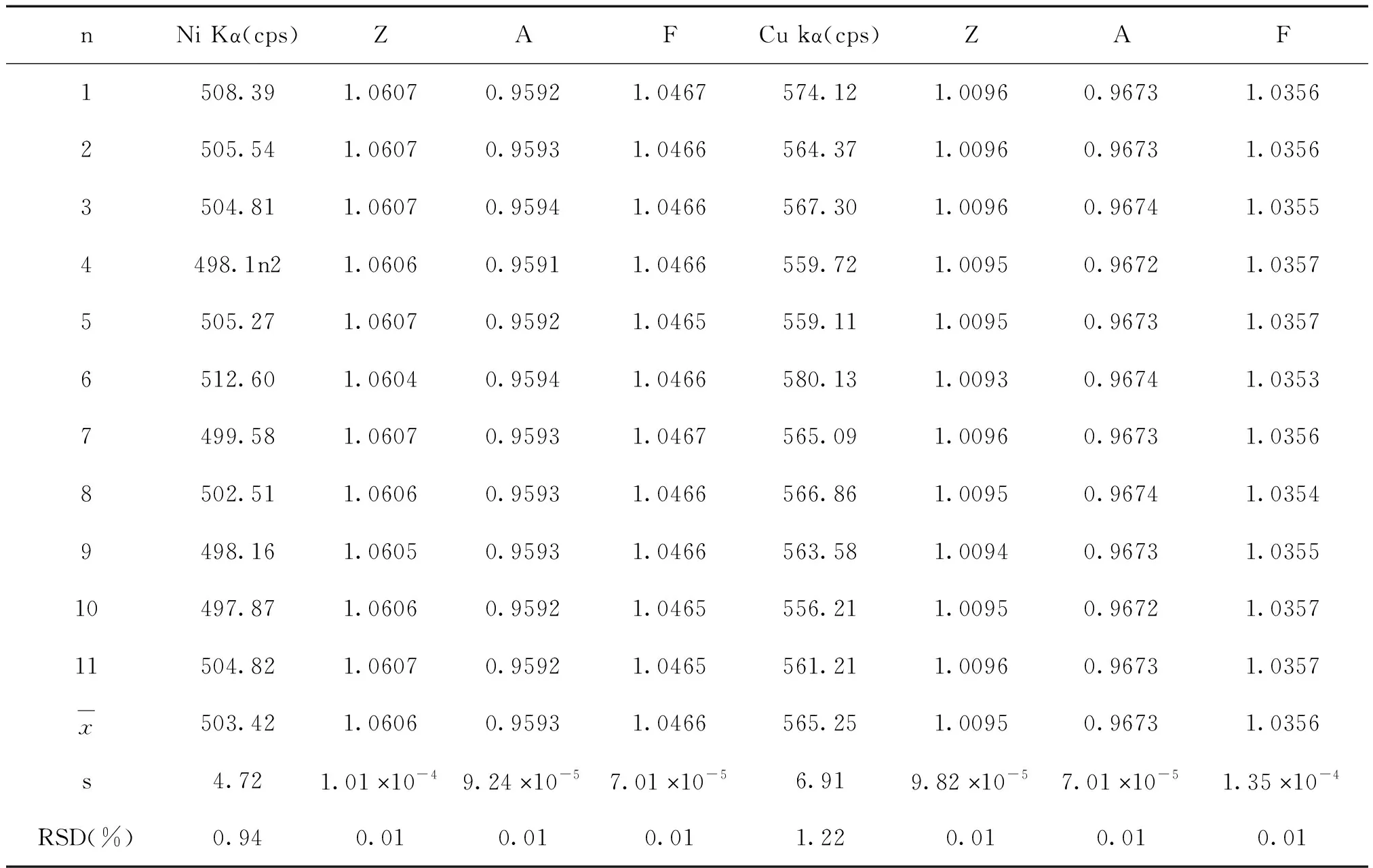
续表1

2.1.2激发电流的大小引起的分析线强度测量的不确定度

理论上分析线净强度与激发电流呈线性关系，但实际中小电流低计数率时，计数率涨落偏差较大；而大电流高计数率时，也会由于计数器的堆积效应出现计数偏差增大[1]，电流的大小是影响定量准确性的主要因素之一。图2a,c分别显示Si和Cu标样中Si Kα和Cu Kα强度与电流的变化关系。Si和Cu元素拟合的线性关系式分别为I=0.42+23.28i(r2=0.99977)和I=0.078+3.84i(r2=0.99992)，其中I和i单位分别为kcps和nA。可以看出，无论是低能量端Si Kα(1.84 keV)还是高能量端Cu Kα(8.04 keV)，在较低电流(0.6 ～ 4 nA)下强度与电流之间均呈现良好的线性关系，但在大电流(>4 nA)情况下，测量值明显偏向电流轴，这主要是由于在高计数率下半导体计数器的堆积效应变得严重，堆积脉冲造成的计数损失的缘故[1]。

图2b,d分别显示Si Kα和Cu Kα强度的线性拟合值与实测值之间的相对偏差随激发电流变化关系。在电流0.8 ～ 4 nA区间，相对偏差小于1%；当电流小于0.8 nA或大于4.5 nA时，相对偏差呈现出逐步放大的现象，最大超过10%。结果表明，测量样品和标样的激发电流大小应该控制在1～3倍范围(1～3 nA)内并尽量接近。

为了考察由于电流大小引起的不确定度，在线性区间改变电流大小并使电子束处正焦状态，测量各元素分析线强度。将各谱线的强度换算为单位电流值计数率，计算不同电流下强度测量的标准偏差和相对标准偏差，结果如表2所示。

实际工作中，同一个样品一般是在同一电流下进行平行测定，所以采用单次测量值的相对标准偏差表示其不确定度较为合理。因此，激发电流的大小引起的Zr Lα、Ti Kα、Ni Kα和Cu Kα强度测量的相对标准不确定度urel(I2)分别为1.24%、1.09%、1.09%和1.19%。

图2 强度与激发电流关系(a, c)和相对偏差与激发电流关系(b, d)

表2 激发电流大小对分析线强度的影响

2.1.3WD引起的分析线强度测量的不确定度

通过调整样品台Z轴值并将电子束调至正焦状态，改变WD的大小。图3显示分析线强度与WD关系。图中上方曲线为EDS探头安装在距离样品台最近位置(L0mm)时各分析线强度的测量值，下方曲线为EDS探头向外拉出11 mm(L0+11 mm)各谱线强度的测量值。由图3可以看出，WD在10.5 ～ 12.3 mm区间各分析线强度出现最大值平台(对应于样品在图4能谱探头几何位置示意图中的B～C区间移动)，平台内强度的测量值变化相对平缓。当WD<10.8 mm或>12.5 mm时，各分析线强度均呈现线性急剧下降，这是由EDS探头的探测几何引起，仪器安装后EDS探头的仰角是固定的，WD过小或过大使得点光源进入探头的出射角过小或过大，部分X射线被遮挡无法通过探头准直器进入检测器。图3中下方曲线表明，探头远离样品台时强度测量值减小，但强度值最大的平台区间以及强度随WD的变化趋势未出现显著改变。

实际测量中，当更换检测样品时，样品的实际高度不可避免会改变，应通过调整样品台Z轴以控制WD在合理的区间，否则将会导致分析线强度测量值的显著偏离，定量分析将产生较大误差甚至错误结果。在上述的平台区间强度的变化相对平缓，当样品由图4中B点向C点移动时，WD不断增大，X射线点光源到达检测器的距离有所增加，根据X射线在自由空间的衰减与传播距离平方成反比的规律，谱线的强度呈现出逐渐降低的趋势(如图3所示)。这种由WD变化导致强度的改变可以归属于仪器本身的缺陷引起的，由此引起的测量不确定度，可以参照B类不确定度进行评估[9]。

图3 分析线强度与WD关系

图4 能谱探头几何位置示意图

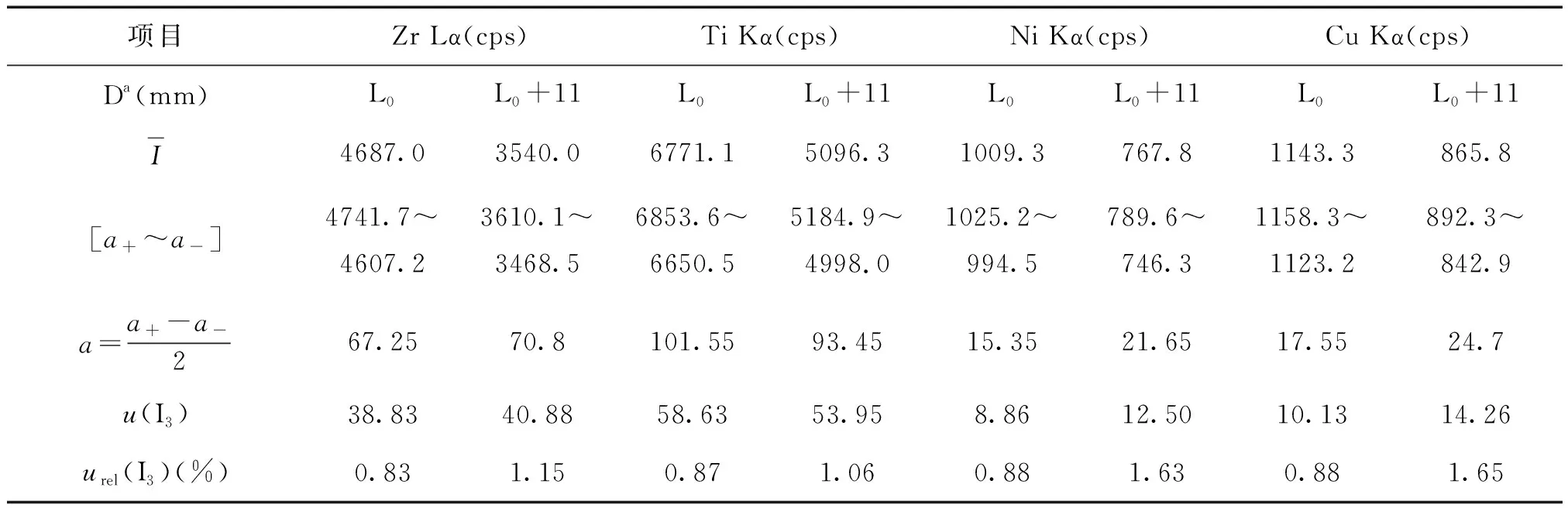
表3 元素分析线强度的变化(WD：10.5～12.3 mm，n=17)

2.1.4 电子束焦距引起的分析线强度测量的不确定度

表4 电子束焦距对分析线强度的影响

续表4

2.1.5取样点大小引起的分析线强度测量的不确定度

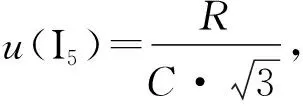
表5 取样点大小对分析线强度的影响

综合上述5种影响因素，由Zr Lα强度引起的测量相对标准不确定度

同样，由Ti Kα、Ni Kα和Cu Kα强度引起的测量相对标准不确定度分别为1.49%、1.77%和1.76%。

2.2 电流示值可读数和稳定性引起的测量不确定度

2.2.1电流示值可读数引起的不确定度

2.2.2电流的稳定性引起的不确定度

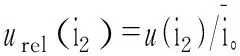
因此，urel(i)=urel(i1)+urel(i2)≈urel(i1)=0.23%

表6 激发电流稳定性引起的不确定度

2.3 ZAF因子引起的测量不确定度

由表1可知，ZAF因子引起的测量值的相对标准不确定度远小于分析线强度引起的测量值的相对标准不确定度urel(I)，因此该不确定度分量可以忽略。

urel(Z)≈0，urel(A)≈0，urel(F)≈0

2.4 标准样品的示值不确定度引起的测量不确定度

本研究所使用的标准样品的证书值分别为ZrO2( 75.23%0.14%)、TiO2(99.960.10%)、NiO (99.95%0.15%)和Al2O3( 99.990.18% )，假设置信度为95%，包含因子为k=2，根据置信区间的大小换算成各元素示值的相对标准不确定度分别为0.09%，0.05%：0.08%和0.09%。Cu和Si为纯元素标样，证书中未给出不确定度，其含量分别为99.99%和99.9%，如按化学分析法推算，其示值的相对误差应<0.1%。由此可见，无论是选择氧化物还是纯元素作EDS定量分析标样，元素示值的相对标准不确定度都要远小于分析线强度引起的相对标准不确定度，由标准样品的示值引起的不确定度分量可以忽略，urel(w0)≈0。

2.5 测量结果的相对合成不确定度

根据公式(3)计算测量值的相对合成不确定度

Zr、Ti、Ni和Cu测量结果的相对合成不确定度分别为2.34%、2.13%、2.52%和2.51%。

2.6 测量结果的相对扩展不确定度

取置信度为95%，包含因子k=2，则Zr、Ti、Ni和Cu测量结果的相对扩展不确定度分别为4.68%、4.26%、5.04%和5.02%

2.7 EDS定量分析结果与分析报告

在电压20 kV, 电流1.00 nA，WD为11.0 mm条件下，用EDS对合金样品进行定量分析。表7为样品A、B两面EDS定量分析结果。考虑合金的表面会有氧化层，保留O元素。对于元素分布均匀、表面光洁的A面，无论是点分析还是面分析，不归一化元素的总量均接近100%，与微束定量结果一般要求相符[7]，定量结果准确。B面背散射图(图1B)显示其表面元素分布不均匀，且表面不光滑不平整，对其点分析结果元素总量为108.88%，超过100%较多，结果不可靠；采用大面积取样分析，元素总量结果较理想(如表7所示)。结果表明增大取样点的面积可有效提高表面不均匀、不平整的样品分析准确度。

样品A面Zr、Ti、Ni和Cu元素3次测量平均值分别为37.48%、33.87%、10.49%和15.27%。取置信度为95%，包含因子k=2，则：

钛非晶合金样品中Zr、Ti、Ni和Cu元素含量分别为37.48%1.75%；33.87%1.44%；10.49%0.53%；15.27%0.77%；k=2。

表7 样品A、B两面EDS定量分析结果

3 结论

(1)EDS定量分析过程中能谱参数对测量结果的不确定度产生影响，结果的准确性主要取决于样品和标准样品分析线强度测量的准确性。

(2)影响强度测量的不确定度来源包括随机变量、激发电流的大小、工作距离、电子束焦距以及取样点大小等因素。其中，激发电流的大小对强度测量产生重要影响，电流过大或过小均会导致强度测量误差显著增大，样品和标样的激发电流大小应该控制在1～3倍范围内并尽量接近；另一个对强度测量产生显著影响的参数是WD，WD应控制在一定范围内(仪器安装时由仪器厂家提供或通过测试确定)，使得强度测量值处于最大值平台内。

(3)通过控制激发电流和WD参数，EDS对钛非晶合金中的Zr、Ti、Ni和Cu元素含量测量的相对扩展不确定度分别为4.68%、4.26%、5.04%和5.02%，k=2。

(4)EDS定量分析的结果符合微束定量分析的一般要求，钛非晶合金中的Zr、Ti、Ni和Cu元素含量测量值分别为37.48%1.75%；33.87%1.44%；10.49%0.53%；15.27%0.77%；k=2。增大取样点的面积可有效提高表面不均匀、不平整的样品分析准确度。