基于偏航角分布的汽车风平均阻力系数计算方法
2021-02-03袁海东刘学龙王海洋
袁海东,刘学龙,高 岳,王海洋
(1. 天津大学 电气自动化与信息工程学院 天津300072;2. 中汽研(天津)汽车工程研究院有限公司 天津300300)
0 引 言
GB 19578—2014《乘用车燃油消耗量限值》[1]以及 GB 18352.6—2016《轻型汽车污染物排放限值及测量方法(中国第六阶段)》[2]对乘用车燃油及排放提出了越来越严格的要求,节能减排成为汽车整车厂和消费者最为关心的问题。影响汽车油耗和排放的行驶阻力包含空气阻力和滚动阻力两部分,在中高速巡航工况下,空气阻力起主导作用。通常,在风洞实验室中通过测量指定车速和零偏航工况下的气动阻力系数评价汽车的空气阻力大小,然而,实际道路的风场条件与风洞自由来流条件存在明显差异,因此风洞测量获得的阻力系数通常小于真实道路上车辆的真实阻力系数。为了减小风洞测量结果与真实道路实际值的差异,本文首先描述了真实道路风场环境特征,分析了影响汽车气动阻力的主要道路环境因素,提出了真实道路环境中偏航角概率分布预估方法以及基于偏航角的风平均阻力系数计算方法,分析了汽车基本尺寸参数对风平均阻力系数的影响规律。
1 真实道路风场条件
由于大气热运动,在地球表面形成自然风,自然风的风速和风向在空间和时间分布不均匀,参考气象数据以及建筑领域的测量数据可以对大气边界层的自然风有定量的认识。汽车的行驶环境处于大气边界层底层(通常小于 2m),通常的测量数据为地面垂向10m以上的数据,大气边界层底层的自然风分布通常需通过数据差值获得,作为大气边界层底层,地面速度为零,地面以上平均自然风速的分布可通过如下公式描述[3]:

其中:UW为地面以上高度 z处的风速,UWG为高度zG处的风速,α为指数系数,可通过α值区分不同地理环境带来的速度剖面的差异,例如,开旷地带α= 0 .16,而城市中心为α=0.4。
大气边界层底层自然风的风速大小和方向本质上在空间和时间不均匀分布,大气湍流对气动力的影响不在本文的研究范畴,读者可参考现有文献[4],本文主要分析自然风对气动力的影响。公式2描述了平均自然风在垂向的分布特征,通常认为自然风的方向为各个方向均匀分布,自然风大小的分布特征通常用威布尔分布描述,如下式所示:
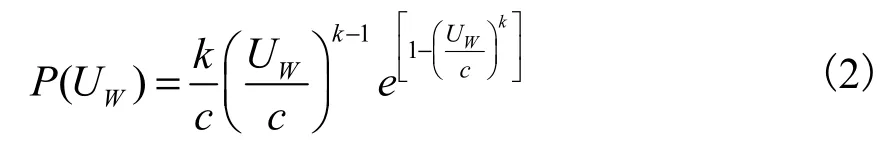
其中:k和c分别为形状系数和比例系数,系数k和c或UW唯一确定威布尔分布特征,形状系数 k与平均风速有关,其平均风速可表示为:

其中:Γ为伽玛函数。
由以上分析可知,在车身高度方向自然风并非大小一致,而是存在剪切速度梯度,根据文献研究可知[5],可以采用车身高度40%位置处自然风速等效车身高度方向的剪切速度分布。因此,自然风对气动力的影响问题可简化为以车身 40%位置处的风速为均匀风速对气动力影响的问题。
2 真实道路环境偏航角分布预估
如图 1所示,车速、平均风速和合成风速组成速度三角形,由此速度三角形可以得出偏航角与风向角和平均风速的关系,如公式4所示。
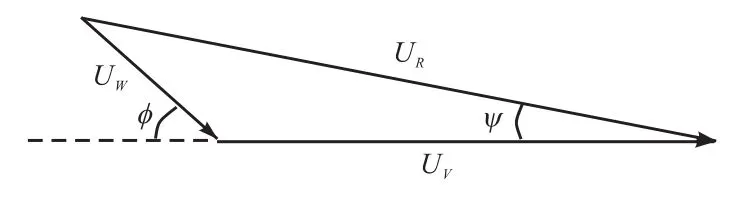
图1 车速、风速、合成风速组成的速度三角形Fig.1 Speed triangle composed of vehicle speed,wind speed,and synthetic wind speed

其中:UV为车速,UW为风速,UR为合成风速,θ为风向角,ψ为偏航角。
基于自然风大小的威布尔分布和风向均匀分布的假设,可对偏航角的概率分布进行预估,本文中自然风大小的威布尔分布特征参考现有文献数据[3],其中形状参数 k=2,取开旷地带的平均风的垂向分布特征进行分析,取垂向地面以上 0.6m位置的平均风速11.54km/h进行计算,如图2所示。
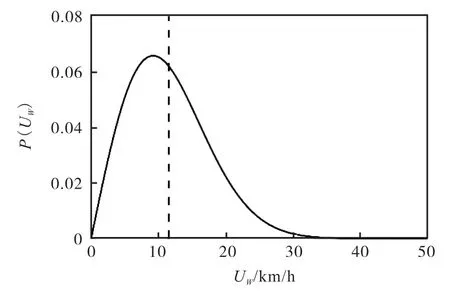
图2 道路风风速概率密度函数Fig.2 Wind speed probability density function
针对偏航角计算中的风速采样数 m和风向角间隔进行参数敏感性分析,如图 3所示。可以看出,在所分析的变化范围内,风速采样数在m=10000达到收敛,而风向角间隔对结果影响不大,在 0.1°时达到收敛。因此,本文选择风速采样数和风向角间隔分别为 10000和 0.1°。

图3 自然风大小采样数和风向角间隔对偏航角预估的影响分析Fig.3 Analysis of influence of natural wind sampling number and wind direction angle interval on yaw angle estimation
3 风平均阻力系数估算
通常,对于给定车速的风平均阻力系数可以由如下公式进行计算,

其中:CD(ψ)为给定车速UV、偏航角为ψ的阻力系数,P(UW)为风速UW的概率分布函数。
根据风速和风向的分布特征的区别,偏航角的预估方法主要分为 MIRA、SAE和 TRRL等方法[6]。MIRA法和 SAE法认为风向为各个方向均匀分布,MIRA法使用风速的威布尔分布,而 SAE法则使用平均风速计算;TRRL法则与 MIRA法和SAE法不同,TRRL法使用平均风速,认为风向角具有不同的概率分布特征。
上述公式给出的是给定车速下的风平均阻力系数,根据汽车阻力系数的雷诺数效应可知,随着雷诺数的增大,阻力系数降低,当雷诺数超过临界值后,车速增加阻力系数基本维持不变。因此,通常阻力系数或风平均阻力系数均指的是超过临界雷诺数以上的结果,这时,UW≪UV,公式5可近似为:
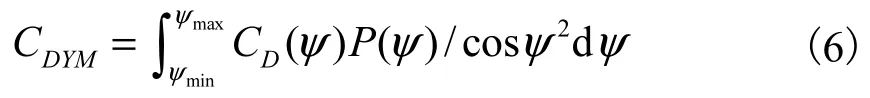
其中:P(ψ)为给定车速下的偏航角概率密度函数,可以通过上述偏航角预估方法获得,ψmin与ψmax为偏航角的最小值和最大值。
公式 6为基于偏航角概率分布的风平均阻力系数计算公式。
基于偏航角的风平均阻力系数计算需要给定车速下指定偏航角的阻力系数,通常风洞测量或数值计算可以获得有限个偏航角下的阻力系数,通过对这些数据进行插值可以获得任意偏航角下的阻力系数,如图4所示,本文使用三次样条曲线进行插值。
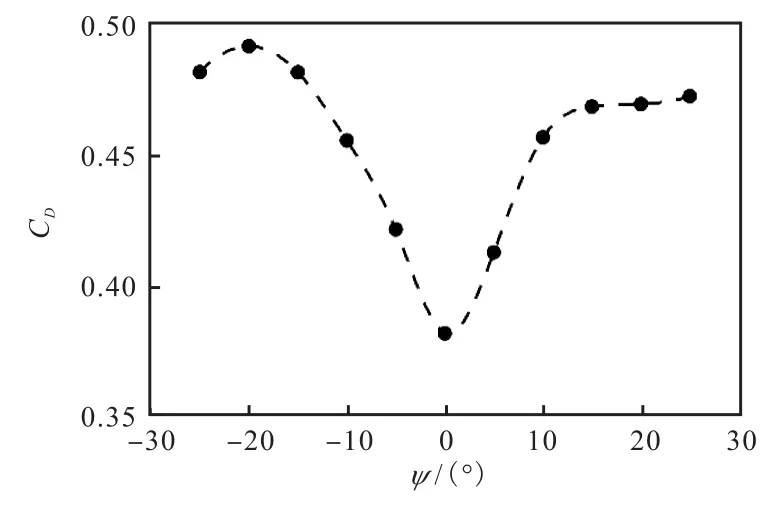
图4 车辆偏航角阻力系数的插值Fig.4 Interpolation of drag coefficient of vehicle yaw angle
本文使用的试验数据参考现有文献中的风洞试验数据[7],如图5所示,一共28款不同车型的试验车参与计算,其中包括 MPV(N=1~7),小型两厢掀背(N=8~14),SUV(N=15~21),三厢轿车(N=22~28)。车速为 UV=97.2km/h(27m/s),平均道路风速为 UWM=11.54km/h。

图5 不同车型的零偏航阻力系数Fig.5 Zero yaw drag coefficient of different models
图 6显示 3种不同的风平均阻力系数的计算结果与零偏航阻力系数的差值ΔCD。可以看出,3种计算方法的计算结果具有相近的特征,3种计算方法都可以用于考虑道路环境风的风平均阻力系数的计算,结果也说明平均阻力系数比零偏航阻力系数平均高出约0.02,这对车辆的实际油耗和续航里程有显著的影响。另外,不同车型的阻力系数对道路风的敏感性不同,其中不同 MPV车型的风平均阻力系数的差异性最大。
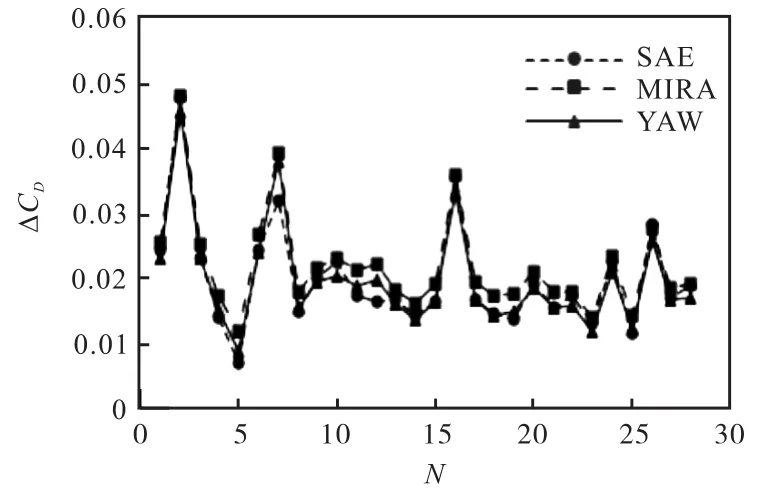
图6 不同平均阻力系数计算结果与零偏航的差异对比Fig.6 Comparison of difference between calculation results of different averaged drag coefficients and zero yaw
在SAE、MIRA和基于偏航角的风平均阻力系数计算方法(YAW)中,SAE方法的计算速度最快,MIRA的计算速度最慢,YAW方法计算效率居中。如图 7所示,SAE方法计算结果较 MIRA方法波动较大,相比之下YAW方法的计算结果与MIRA更为接近。偏航角相比于道路风风速的分布更容易通过道路测量获得,因此提出基于偏航角的风平均阻力系数计算方法具有一定的工程使用价值。
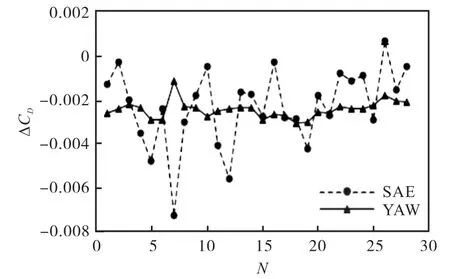
图7 SAE和基于偏航角的平均阻力系数与 MIRA计算结果的差值对比Fig.7 Comparison of difference between SAE and averaged drag coefficient based on yaw angle and MIRA calculation results
4 风平均阻力系数对车型尺寸参数的敏感性分析
如图8所示,分析了风平均阻力系数对车型尺寸参数的敏感性,图中虚线为所有数据的线性拟合。可以看出,风平均阻力系数对车长(L)和车宽(W)并不敏感,甚至增加车长和车宽可以轻微降低道路风对阻力系数的影响,风平均阻力系数与零偏航阻力系数的差值随车高(H)和正投影面积(A)的增加而增大,综合考虑,车高是影响车辆阻力系数对道路环境风响应的敏感参数,车高越高道路风对车辆的气动阻力系数影响越大。
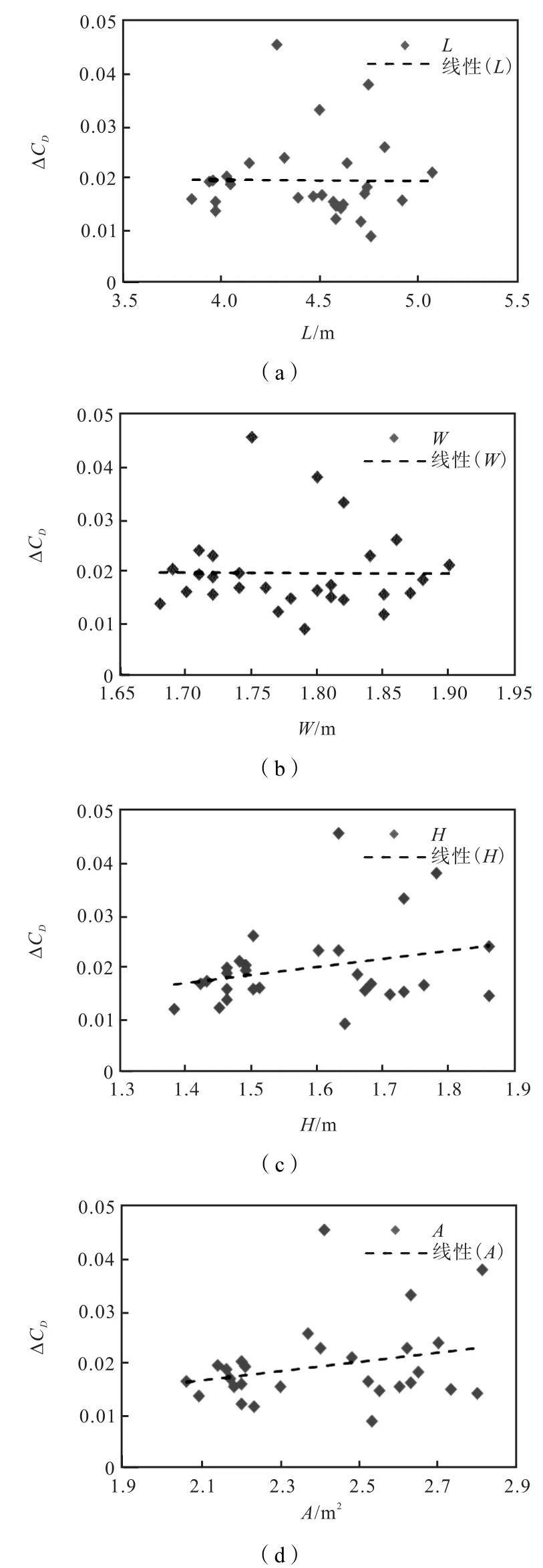
图8 风平均阻力系数对车型尺寸参数的敏感性分析Fig.8 Sensitivity analysis of averaged wind drag coefficient to model parameters
5 结 论
①首先提出基于道路环境风风速概率分布的汽车真实道路偏航角概率分布的计算方法,进而提出基于道路偏航角概率分布特征的风平均阻力系数计算方法。
②基于偏航角的风平均阻力系数的计算结果和MIRA以及 SAE方法的计算结果基本一致,相比于SAE方法,基于偏航角的计算方法与 MIRA方法的结果更为接近。
③考虑道路自然风的影响,车辆的风平均阻力系数受车辆高度的影响较大,与车辆的长度和宽度的相关性不大。
