基于人群搜索算法和增广乘子法的混合可靠性分析

黄 杨 王林军 杜义贤 彭云龙 廖 玮

（1.三峡大学 水电机械设备设计与维护湖北省重点实验室, 湖北 宜昌 443002；2.三峡大学 机械与动力学院, 湖北 宜昌 443002）

结构在规定时间和规定条件内完成规定任务的能力称为结构可靠性.机械结构可靠性是工程设计及应用中重要的约束条件之一,是评估结构的安全性、维持机构的功能要求.由于受到产品的材料属性、加工精度以及装配误差等影响,在进行结构可靠性分析和设计时,存在着诸多不确定性.这种影响结构可靠性的不确定性又可分为随机性、模糊性和知识的不完善性.

目前,研究可靠性时通常考虑的是随机不确定性下的可靠度.近年来,研究者为了解决实际工程问题,提出了许多新的计算方法[1-5],尤其是结构可靠性分析领域.Ashok Bakkiyaraj[6]等针对复合电力系统可靠指标分析,提出了二进制差分进化算法(BDE),将此搜索方法应用于RBTS和IEEE-RTS测试系统,可分析较少数目系统状态的可靠性；谢少军等[7]针对耦合区间造成的可靠性分析计算效率低的问题,采用了序列迭代分析方法来解决这一问题；Zadeh[8]等提出了一种基于元模型的优化结构设计方法,来求解多学科多目标的优化设计问题,通过引入SQP法和元模型,来做出位于Pareto解处的模糊逻辑决策；游令非等[9]针对目前结构普遍存在模糊变量和随机变量混合的情况,通过改进包络函数来计算机构运动时变可靠度；王元帅[10]提出了一种基于蒙特卡洛法的可靠性分析,用来确定各参数的随机性对结构可靠性分析的影响；姜潮等[11]通过结合两种概率模型来研究可靠性指标与变量之间的关系,来分析区间变量与概率变量对可靠度指标的影响；邱涛等[12]针对结构中既含有区间变量又含有随机变量提出了一种二参数寻优设计点的混合可靠性分析方法,对于非线性程度较高的目标函数有较高的计算精度；孟增等[13]针对功能函数非线性程度较高时,HL-RF算法会出现混沌、震荡和周期解现象,提出了一种新的修正控制理论算法来解决迭代过程中的震荡问题,该法效率较高,且较为稳定.

如今可靠度计算方法多是建立在假设影响结构的随机变量都是相互独立的基础上的,很少考虑随机变量的相关性对可靠指标的影响,且系统可靠性问题通常存在大量的不确定参数,若忽略了参数不确定性和变量间的相关性就会给可靠指标的计算带来误差.在进行可靠性分析时,传统的一次二阶矩法、二次二阶矩法都需要求解结构极限状态方程对随机变量的偏导数,Monte Carlo法则需要模拟多次才能得到精确解.人群搜索算法在求解可靠度指标时,则不需要求解结构极限状态方程对随机变量偏导数,且寻优能力较强.

鉴于此,本文提出一种基于人群搜索算法和增广乘子法的混合可靠性分析方法.该方法以可靠指标最小为目标函数,以影响结构可靠指标的随机变量构成的极限状态方程为约束条件建立数学模型,进行结构可靠性分析,为存在复杂参数相关性的结构可靠性优化问题提供了有效工具.

1 本文算法介绍及可靠度指标的建立

1.1 人群搜索算法

人群搜索算法(SOA)是直接模拟人的随机搜索行为,它将对人的智能搜索行为运用到对优化问题的搜索上.所谓随机搜索行为就是指：在搜索过程中当搜寻者的位置较好时,则在其较小领域内搜索；当搜寻者的位置较差时,则扩大搜索范围,在较大领域内搜索.SOA以搜索队伍为种群,以每个搜寻者的位置作为候选解,以适应度值的大小来评判候选解的优劣,利用搜索步长和方向进行更新,来完成对问题的优化求解.

首先通过公式(1)来确定第i个个体在j维搜索空间上的搜索步长αij.

式中：ω为惯性权值,随进化代数增加从0.9线性递减至0.1；iter,itermax分别为当前迭代次数和最大迭代次数分别为当代种群中最大和最小函数值的位置；δij为隶属度函数的参数；uij为j维搜索空间目标函数值i的隶属度；D为搜索空间维数.

通过对人的利己行为、利他行为和预动行为分析和建模,得到任意第i个搜寻个体的利他方向利己方向和预动方向,见式(2)：

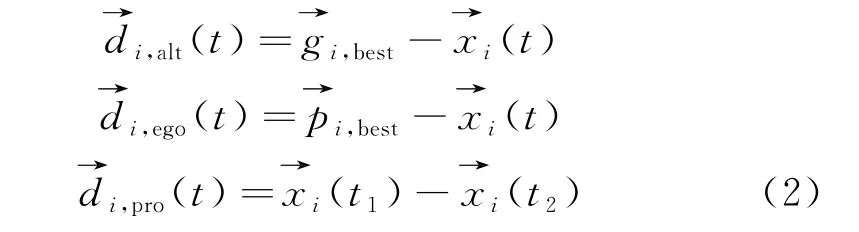
再对以上3个方向随机加权几何平均,确定搜索方向,可得到第i个个体在j维搜索空间上的搜索方向,见式(3)：

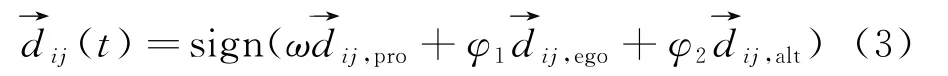
利用搜索步长和方向来进行位置更新,更新公式见式(4)：

人群搜索算法的流程图如图1所示.

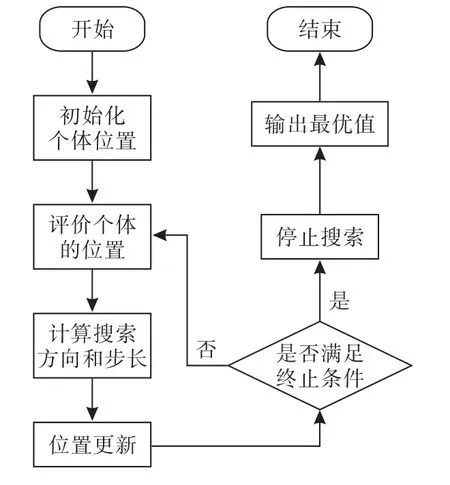
图1 人群搜索算法流程图

1.2 等式约束增广乘子法

在解决带约束问题的方程时,为了将有约束问题转换为无约束问题,通常使用的方法有拉格朗日乘子法和罚函数法.为了避免罚函数法的罚因子选取对计算精度的影响,可将拉格朗日乘子法和罚函数法相结合构造无约束目标函数,即为增广乘子法.此方法同时结合了拉格朗日乘子法和罚函数法的优点,同时可避免初始罚因子的选取问题.

对于等式约束问题的数学模型：

则定义如下的拉格朗日增广函数：

1.3 可靠度指标模型的建立

设X1,X2,…,Xn是影响结构功能的基本随机变量,则可写出结构的功能函数：

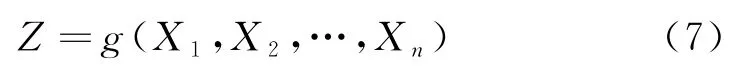
当Z＞0时,表示结构是处于可靠状态的；Z＜0时,表示结构是处于失效状态的；Z=0时,表示结构处于极限状态面上.据此,可构建结构极限状态方程：

用拉科维茨-菲斯莱法将非正态变量当量正态化,得到正态分布的均值,标准差及可靠指标β：

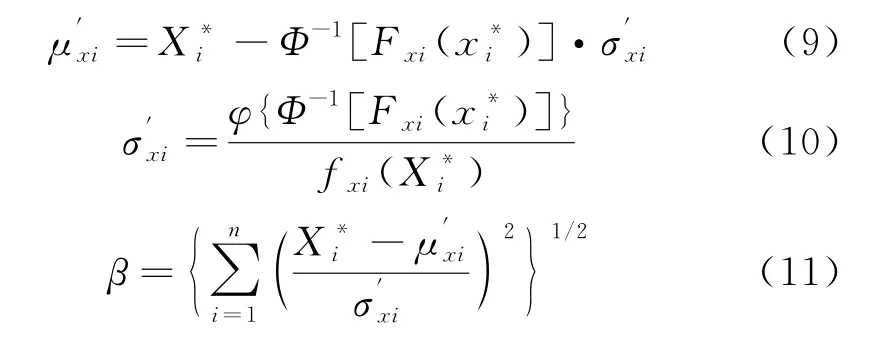
由于验算点未知,故可将β看作极限状态曲面点p(X1,X2,…,Xn)的函数,通过求解找到β的最小值,即得到可靠指标β和验算点p*(,,…,).由上,可建立以下优化数学模型：

运用等式约束增广乘子法将上述带约束的数学模型化为无约束数学模型,公式为：

式中：M(X*)即为β2；右端第2项为惩罚项,其中r为罚因子；右端第3项为乘子项,λ为拉格朗日乘子.

在使用增广乘子法时,罚因子只需取一个较大的数值即可,并不要求罚因子趋近于无穷大,这样就避免了单纯使用罚函数法罚因子的选取问题.

2 算 例

2.1 数值算例

设变量x1和x2均服从正态分布,其均值分别为0和0,标准差分别为1和1,极限状态方程为：

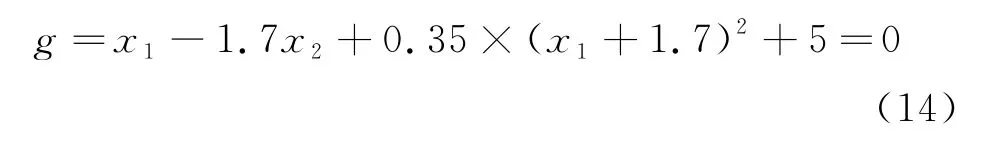
分别使用本文算法、一次二阶矩法(FOSM),蒙特卡罗法(MCS)求解其可靠性指标.得到的可靠性指标计算结果见表1,本文算法和FOSM法可靠指标及失效概率迭代对比图,如图2所示.

表1 3种方法可靠指标计算结果

通过表1可看出,本文算法计算所得的可靠指标为2.545 9；FOSM法计算所得的可靠指标为2.552 9；MCS法计算所得的可靠指标为2.624 4.这3种算法计算的可靠指标大致相同,验证了本文算法的可行性.同时本文算法只需要迭代3次就可以得到可靠性指标,而FOSM法需要迭代9次,且由图2可知,本文算法收敛速度更快,且较为稳定,故本文算法更优.

图2 本文算法和FOSM法的对比

2.2 汽车正面高速碰撞

如图3所示,考虑汽车正面耐撞的可靠性优化设计问题,研究汽车高速碰撞时对乘员的伤害.由于汽车正面高速碰撞时,要求尽可能减小乘员所受伤害,且需保证有足够的安全空间,故可将衡量车身的安全指标定义为发动机上下两个标记点的侵入量,且应小于给定的额定值[14].

图3 高速正面碰撞

本文选取发动机下标记点侵入量为安全指标,且应小于给定的额定值=350 mm,变量X1～X3均为正态随机变量,分别表示为前保险杠厚度和吸能盒内、外板厚度；Y1,Y2为区间分布变量,分别表示为前纵梁内、外板厚度.车辆有限元碰撞模型如图4所示,随机变量参数取值和分布类型见表2.其中对于正态随机变量,参数1和参数2分别表示均值和标准差；对于区间变量,参数1和参数2分别表示变量的上边界与下边界.

图4 高速正面碰撞的有限元模型

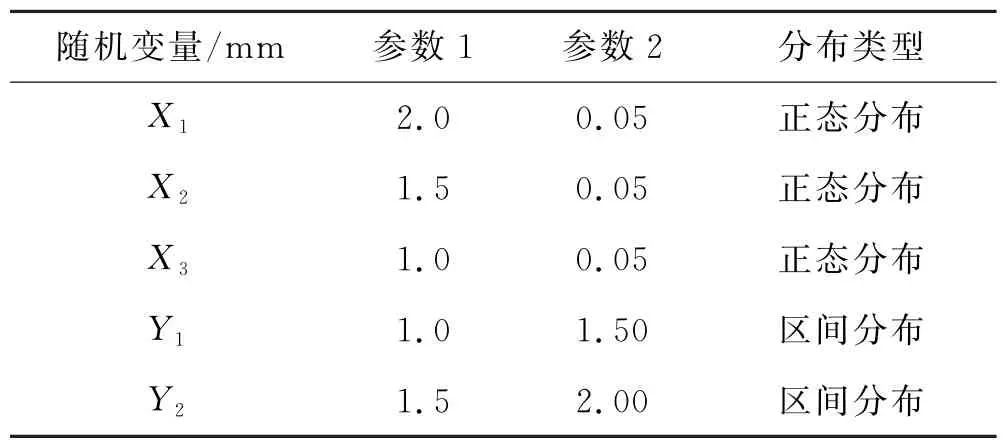
表2 不确定变量分布类型和参数取值情况

通过使用有限元分析软件建立汽车碰撞模型,再对仿真模型进行采样,来构建功能函数的二阶响应面[15].其功能函数可表示为：

使用本文算法,求得其可靠指标β=4.388,失效概率Pf=5.715 7×10-6；使用MCS算法,求得其可靠指标β=4.363,失效概率Pf=6.400×10-6.两种算法计算结果近似相同,同时可看出其失效概率接近于0,说明了该算例在本文条件下具有较高的可靠性.

在进行结构可靠性分析与设计时,由于实际情况和成本因素等限制,常缺乏足够准确的样本信息来描述系统,从而会产生各种不确定性因素[16].同时在计算过程中大多都假设各随机变量彼此之间相互独立,而忽略了参数之间相关性问题可能会对计算结果带来的误差.下面通过上述工程算例来讨论均值和标准差不确定性以及参数之间存在相关性时,对可靠指标计算结果的影响.

1)若考虑变量均值μ不确定性,并保证标准差σ不变,应用本文方法计算所得可靠指标β变化范围及其不确定度情况见表3.

表3 考虑均值不确定性的可靠指标

由表3可知均值不确定度与可靠指标不确定度的对应关系如图5所示.由表3和图5可知,随着均值不确定度不断变化,其可靠指标不确定度也发生了变化,且呈正相关关系.

图5 可靠指标受均值不确定度的影响

2)若考虑标准差σ不确定性,并保证均值μ不变,应用本文方法计算所得可靠指标β变化范围及其不确定度情况见表4.

表4 考虑标准差不确定性的可靠指标

由表4可知标准差不确定度与可靠指标不确定度的对应关系如图6所示.

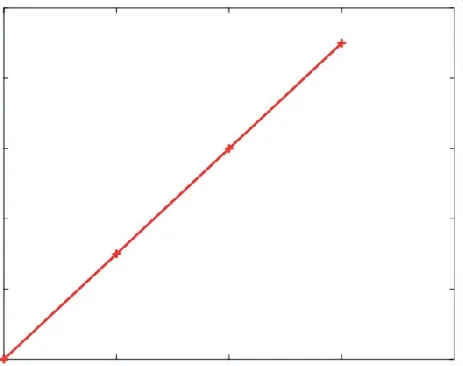
图6 可靠指标受标准差不确定度的影响

由表4和图6可知,随着标准差不确定度不断变化,其可靠指标不确定度也发生了变化,且呈正相关关系.对比均值不确定度和标准差不确定度分别对可靠指标不确定度带来的影响,发现后者对可靠指标不确定度的影响较小.

3)考虑变量间的相关性给可靠性指标带来的影响,设定随机变量X1和X2存在相关性,且两个随机变量与X3、Y1、Y2之间均相互独立,其中相关系数ρx1x2由-0.9到0.9,以0.3为等分点划区间依次取值,应用本文方法所得可靠指标变化情况见表5.

由表5可知相关系数ρx1x2的取值与可靠性指标的对应关系如图7所示.

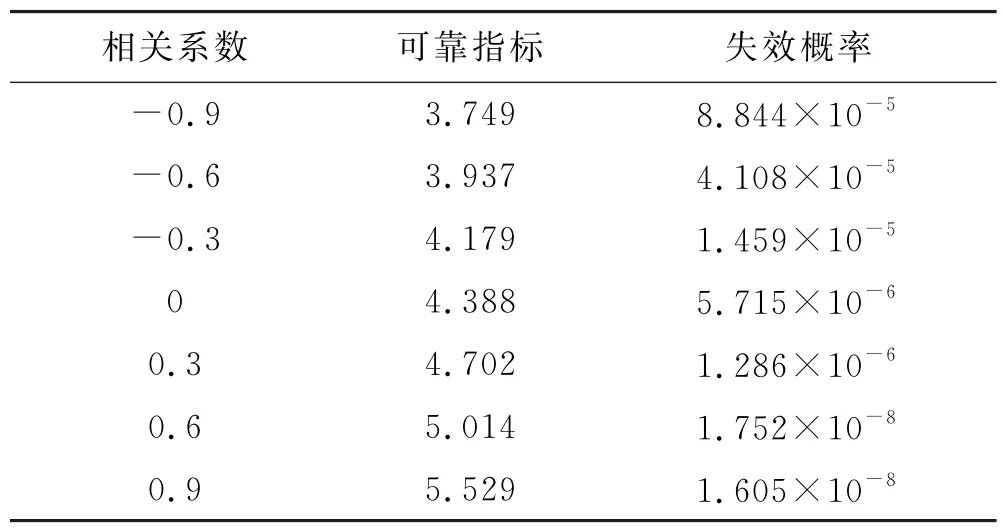
表5 可靠指标变化情况

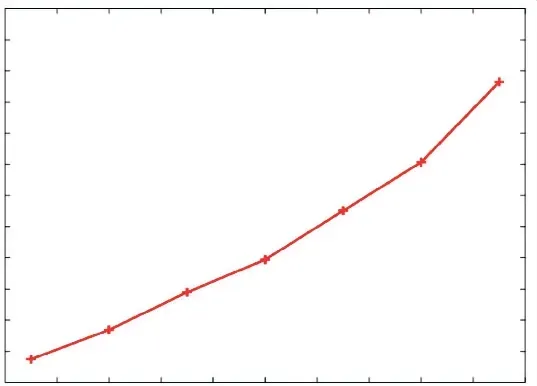
图7 可靠指标受相关系数的影响

由表5和图7可知,随着相关系数ρx1x2增大,该结构的可靠指标也随之增大,可靠性逐渐增强.可见,如果在结构可靠性分析中,忽略了参数的不确定性和随机变量间的相关性,将会给计算结果带来较大影响.

3 结 语

本文提出了一种基于人群搜索算法和增广乘子法的混合可靠性分析方法,为求解考虑不确定性和相关性的结构可靠性优化设计问题提供了有效工具.两个算例验证了本文方法的有效性,结果表明：本文方法在处理具有一定非线性程度的结构功能函数时,与传统算法相比,在保证精度的前提下,迭代次数更少；均值不确定度和标准差不确定度与可靠指标不确定度呈线性相关,且均值不确定度较标准差不确定度对可靠指标的计算有更大的影响；随着变量间的相关系数取值不同,结构的可靠指标也会发生变化.此外,未来可引入Nataf变换的随机响应面法对本文进行拓展,来解决隐式极限状态函数的结构中变量间存在多维相关性的问题.