混凝土MAZARS模型的非局部化及其数值实现与验证

徐 磊 王绍洲 金永苗

（河海大学 水利水电工程学院, 南京 210098）

混凝土是典型的准脆性材料,在破坏阶段具有明显的应变局部化特征[1].现阶段,以有限元为代表的连续介质数值分析方法是开展混凝土材料与结构破坏模拟的主要手段[2].研究表明,在基于传统局部本构模型的混凝土材料与结构非线性有限元分析中,计算结果会依赖于有限元模型的单元尺寸[3],从而丧失客观性.为解决这一问题,Bažant等[4]提出将积分形式非局部理论与传统局部本构模型相结合,通过引入与细观结构相关的材料特征长度与构建体现不同位置材料间力学状态相互影响的非局部变量,实现传统局部本构模型的非局部化,有效克服了基于由局部模型导致的有限元计算结果单元尺寸依赖性.

另一方面,通用有限元软件ABAQUS因其强大的非线性分析能力得以在结构分析中被广泛采用[5].Xu等利用ABAQUS成功实现了混凝土拱坝从局部开裂到整体破坏全过程的有限元模拟[6].然而,ABAQUS中虽内置了面向混凝土材料的损伤塑性模型[7]、弥散开裂模型[8]等本构模型,但本质上均属局部本构模型,故基于ABAQUS的混凝土结构破坏分析难以保证分析结果的客观性.理论上虽可通过编制非局部混凝土本构模型的UMAT用户材料子程序实现基于ABAQUS平台的混凝土结构破坏的合理分析,但在具体实施中却由于受限于ABAQUS中固有的数据传递方式(在UMAT接口中仅能获取当前积分点的相关信息,无法调用该积分点附近其他积分点的信息)而无法完成.

鉴于此,本文首先基于由Mazars提出的宏观尺度混凝土损伤模型[9](简称为MAZARS模型),推导了混凝土单轴受拉条件下以单元尺寸为变量之一的应力与变形量解析表达式,直观地阐明了单元尺寸依赖性的产生原因,进而将MAZARS模型与积分形式非局部理论相结合,给出了积分形式非局部MAZARS模型理论表达.在此基础上,提出了与ABAQUS数据传递方式相适应的非局部MAZARS模型数值实现方法,并完成了相关程序编制.通过算例分析,验证了基于ABAQUS平台的非局部MAZARS模型数值实现的可行性与程序开发的正确性.研究成果不仅在一定程度上拓展了ABAQUS在混凝土材料与结构损伤方面的分析功能,亦可为其他非局部本构模型在ABAQUS中的数值实现提供借鉴与参考.

1 MAZARS本构模型及其非局部化

在各向同性线弹性本构模型的基础上,Mazars通过引入损伤变量d在损伤力学框架内建立针对混凝土材料的宏观尺度本构模型[9],应力-应变关系见式(1)：

式中：E0和v0分别为材料初始弹性模量与泊松比；σij和εij分别为应力和应变张量；σkk为体积应力；δij是Kronecker符号.

在MAZARS模型中,损伤变量d为拉伸损伤变量dt与压缩损伤变量dc的加权组合,见式(2)：

式中：αt与αc之和为1,分别表示拉伸损伤权重系数与压缩损伤权重系数,按式(3)、(4)计算：

式中：〈〉+为Macauley括号；β为模型参数,取值范围一般为分别为主应变中的拉伸、压缩部分为模型中定义的等效应变,可由主应变εi(i=1,2,3)值计算：

在MAZARS模型中,以材料变形历史中产生的最大等效应变为损伤演化方程的自变量k且令其初值为k0,拉伸损伤演化方程与压缩损伤演化方程分别见式(6)、式(7).

式中：k0代表材料进入损伤阶段的控制阈值(即当k=k0时,处于线弹性变形阶段),其值可取为混凝土单轴拉伸状态下的峰值拉应变；At、Bt、Ac、Bc为模型参数,对于一般混凝土材料,0.7≤At≤1.2,1≤Ac≤1.5,104≤Bt≤5×104,103≤Bc≤2×103.

损伤加载函数f(ε~,k)见式(8)：

可以看出,上述MAZARS模型属于局部本构模型,即一点的应力状态完全取决于该点的应变状态,故基于MAZARS模型的有限元计算结果不可避免地存在单元尺寸依赖性,详见下述.

图1为一长度为lT的混凝土杆,左端受水平向位移约束,右端受水平向均布拉伸位移作用,处于单轴受拉状态.为触发单轴拉伸状态下的应变局部化,假定在混凝土杆中部存在初始缺陷,并采用MAZARS模型描述该部位混凝土的力学特性.

图1 混凝土单轴受拉杆件及网格剖分示意图

为分析有限元计算结果的单元尺寸依赖性,假定混凝土杆沿轴线方向被均匀剖分为Ne个单元(如图1所示),则任一单元尺寸(长度)le为

由于在单轴拉伸破坏过程中,混凝土杆将在存在初始缺陷的中部发生损伤开裂(其两侧将始终处于线弹性变形阶段),故包含这一部位的单元拉应变单调增大,而其他单元拉应变则为先增大后减小.

依据式(1)以及中部损伤单元与其他未损伤单元拉应力相等条件,可得：

进一步,可将混凝土杆拉伸变形量U表示为中部损伤单元的损伤变量d、拉应变以及单元尺寸le的函数,见式(11)：

式中：Ne=lT/le.

在单轴应力状态下,混凝土杆应力受控于中部损伤单元拉应变及相应的损伤变量,考虑式(11),其计算表达式见式(12)：

式中：k0=ft/E0,ft为混凝土单轴抗拉强度.

依据式(12)、(13),在给定相关MAZARS模型参数的基础上,即可分别计算出在单元尺寸le特定取值下,对应于不同量值下的混凝土杆拉伸变形、应力量值.

图2为在一组特定MAZARS模型参数下(E0=30 GPa,v0=0.2,At=1.0,Bt=15 000,k0=0.00012),长度为10 cm的混凝土杆在不同单元尺寸下(分别为1.43 cm,2.00 cm,3.33 cm)的单轴拉伸应力-位移曲线.图3为拉伸变形量值为0.001 4 cm时,不同单元尺寸条件下混凝土杆拉应变的轴向分布.

图2 不同单元尺寸下的应力-位移曲线

图3 不同单元尺寸下混凝土杆拉应变轴向分布

从图2可以看出,混凝土杆在损伤开裂阶段的应力变形响应体现出了明显的单元尺寸依赖性.随着单元尺寸的减小,软化段逐渐变陡且未能趋于收敛.从图3可以看出,轴向单元尺寸越小,中部损伤单元的应变集中程度越高.

为消除上述基于MAZARS模型的有限元计算结果单元尺寸依赖性,可将MAZARS模型与非局部积分理论相结合,从而实现MAZARS模型的非局部化.在非局部MAZARS模型中,将等效应变作为非局部化变量,即将式(8)中的局部等效应变替换为非局部等效应变.依据非局部积分理论,材料点x处的非局部等效应变(x)可按式(14)、(15)计算：

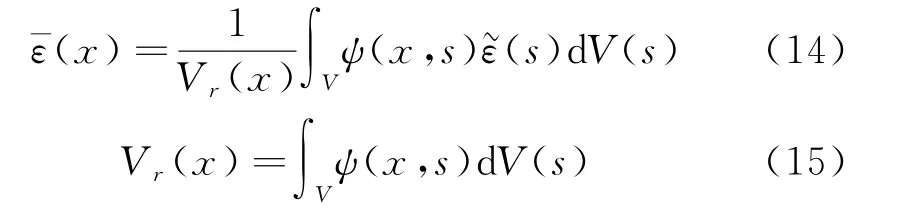
式中：V是对局部等效应变求加权的空间域,其范围受控于材料特征长度lc；s为与x相关的积分域内的材料点；ψ(x,s)为非局部积分权重函数,可按式(16)计算：

从式(14)可以看出,混凝土内任一点的应力不仅与该点自身的局部等效应变相关,还通过损伤变量d与其附近特征长度范围内各点的局部等效应变相关,从而可有效避免由局部模型导致的计算结果网格尺寸依赖性.

2 数值实现方法与程序开发

为便于用户在ABAQUS平台上开发未包括在其内置材料库中的本构模型,ABAQUS提供了用户材料子程序接口UMAT.UMAT用户材料子程序需采用FORTRAN语言开发,在从主程序获取相关数据后,需基于给定的模型参数通过用户开发的程序更新积分点应力、雅可比矩阵,并可根据需要自定义状态变量.

对于局部本构模型的开发,一般情况下均可通过UMAT从主程序获取全部所需的数据,如当前积分点的应变、应变增量等.但对于积分形式的非局部MAZARS模型而言,任一积分点的非局部等效应变计算不仅需要获取其自身的应变,还需要获取其附近在材料特征长度范围内其他积分点的应变数据.由于ABAQUS在计算中是逐个积分点调用UMAT,且仅能通过UMAT获取当前积分点的应变数据,故ABAQUS固有的数据传递方式无法充分满足开发非局部MAZARS模型的内在要求.

在无法改变ABAQUS主程序与UMAT接口之间数据传递方式的前提下,为在ABAQUS中实现基于非局部MAZARS模型的混凝土损伤有限元分析,本文借鉴Pereira等[10]在LS-DYNA中开发非局部本构模型时所采用的方法,提出一种用于不需要获取当前迭代步中其他相关积分点应变数据的积分点非局部等效应变近似方法,详述如下.

假定需要计算非局部等效应变的某积分点在前一增量步(nthIncrement)完成平衡迭代后的非局部等效应变与局部等效应变分别为与,并定义该积分点在当前增量步((n+1)thIncrement)的非局部化比例因子kn+1为

为计算该积分点在当前增量步平衡迭代过程中的非局部等效应变,首先基于该积分点当前状态下的应变全量,按式(5)计算当前状态下的局部等效应变,在此基础上,利用式(17)计算出的当前增量非局部化比例因子,计算出与相应的该积分点当前状态下的非局部等效应变,见公式(18)：

由于式(18)假定该积分点在当前增量步中的非局部等效应变与局部等效应变比值和前一增量步相同,故按式(18)计算出的非局部等效应变与按式(14)计算出的非局部等效应变一般并不一致.但已有研究表明[11],在当前增量步步长较小的条件下,上述二者之间的差异不大,故若分析中设置较小的增量步长,则由式(18)计算出的非局部等效应变可视为实际非局部等效应变的近似值.

在上述基础上,本文提出了可与ABAQUS数据传递方式相适应的的非局部MAZARS模型数值实现方法,基本思路是：(1)通过UMAT实现在当前增量步的任一迭代步中各积分点局部等效应变的计算与COMMON BLOCK存储、非局部等效应变计算、应力与雅可比矩阵更新等；(2)通过UEXTERNALDB实现在前一增量步完成平衡迭代后各积分点非局部化比例因子的计算与COMMON BLOCK存储；(3)通过USDFLD实现各积分点位置坐标的获取与COMMON BLOCK存储；(4)通过共用COMMON BLOCK实现UMAT与UEXTERNALDB、UEXTERNALDB与USDFLD之间的数据传递.

UMAT用户材料子程序主要计算步骤如下：

(1)获取由ABAQUS主程序传递至UMAT中的非局部MAZARS模型参数、应变、状态变量等数据,获取非局部化比例因子(在UEXTERNALDB中计算并存储于COMMON BLOCK中).

(2)形成弹性矩阵.

(3)计算全量应变列阵,并通过调用ABAQUS内置的实用程序SPRINC计算主应变.

(4)依据式(5)计算局部等效应变,并更新UMAT与UEXTERNALDB共用的COMMON BLOCK中该积分点的局部等效应变.

(5)依据式(18)计算非局部等效应变.

(6)依据非局部MAZARS模型的损伤加载函数进行加载判断,若为加载,则更新非局部等效应变历史最大值、损伤变量值,反之,则保持非局部等效应变历史最大值、损伤变量值不变.

(7)进行应力、雅可比矩阵DDSDDE更新.

对于任一增量步,在其完成平衡迭代后,通过调用ABAQUS内置的实用程序UEXTERNALDB,依据式(14)与存储在COMMON BLOCK中各积分点的局部等效应变与位置坐标(由ABAQUS调用实用程序USDFLD读取各积分点位置坐标并存储于COMMON BLOCK中),计算该增量步结束后各积分点的非局部等效应变,进而更新各积分点的非局部化比例因子.

在非局部损伤有限元分析过程中,ABAQUS主程序对上述UMAT子程序的调用是在积分点的层次上进行的,即在每次整体平衡迭代过程中,均需在对单元循环的基础上对单元中的积分点循环,从而逐一完成每个积分点的应力、雅克比矩阵与状态变量更新.

3 算例分析与验证

为了验证第2节中所提出的非局部MAZARS数值实现方法的可行性与程序开发的正确性,进行了如下算例分析.

用在ABAQUS中二次开发的非局部MAZARS模型,对一混凝土单边切口梁(见图4)的三点弯曲试验进行数值模拟,并对切口(5 mm×50 mm)附近一定范围(40 mm×150 mm)分别采用3种不同单元尺寸,即大尺寸5 mm、中尺寸2.5 mm、小尺寸1.25 mm.

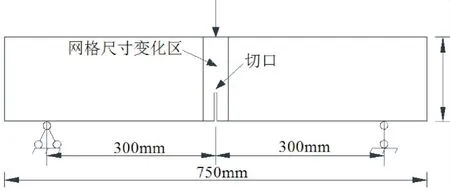
图4 混凝土单边切口梁试件简图(单位：mm)

为便于对比分析,首先在一组给定的MAZARS模型参数取值下(E0=30 GPa,v0=0.2,k0=0.000 1,At=1,Bt=15 000,Ac=1.2,Bc=1 500,β=1),对具有不同单元尺寸的数值试件开展基于MAZARS模型的数值模拟.模拟中,试件底面左、右侧支撑处分别施加竖向和水平向、竖向位移约束,顶面中部按位移加载方式施加量值为1mm的竖直向下位移荷载.

图5给出了不同单元尺寸下模拟所得的力与位移关系曲线,图6给出了不同单元尺寸下模拟所得的等效应变分布.

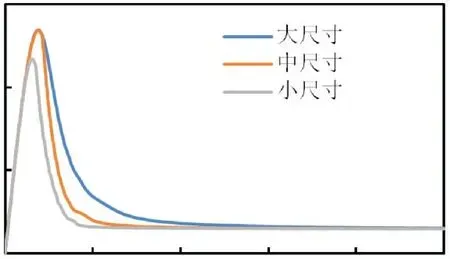
图5 不同单元尺寸下荷载-挠度曲线(局部)

从图5可以看出,在线弹性变形阶段,试件的受力变形响应基本一致,但在峰后软化阶段,试件的受力变形响应呈现出明显的单元尺寸依赖性,随着单元尺寸的减小,试件的“脆性”趋于增强；从图6可以看出,基于MAZARS本构模型计算所得的局部等效应变分布特征明显受控于单元尺寸,单元尺寸越小,局部等效应变越集中,这实际上也是试件“脆性”增强的原因所在.以上分析表明,基于MAZARS模型的损伤有限元分析无法保证结果的客观性.

图6 不同单元尺寸下局部等效应变(变形放大30倍)

针对具有不同单元尺寸的3个数值试件,分别开展基于非局部MAZARS模型的单轴拉伸模拟(材料特征长度取为15 mm,其他模型参数与局部分析相同).图7给出了不同单元尺寸下基于非局部MAZARS模型模拟所得的荷载-挠度曲线,图8给出了不同单元尺寸下模拟所得的非局部等效应变分布.

图7 不同单元尺寸下荷载-挠度曲线(非局部)

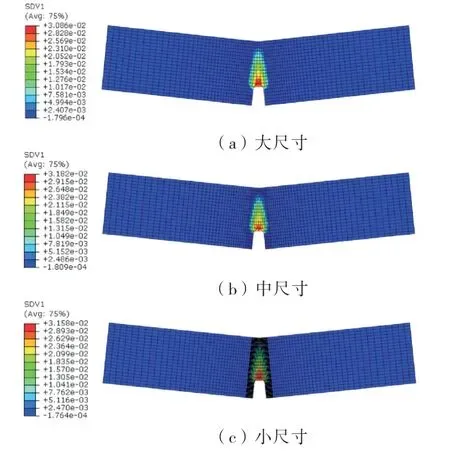
图8 不同单元尺寸下非局部等效应变(变形放大30倍)

从图7可以看出,不同单元尺寸下,试件的荷载-挠度曲线基本一致,表明采用非局部MAZARS本构模型可有效避免结构受力变形响应的单元尺寸依赖性；从图8可以看出,基于本文所开发非局部MAZARS模型子程序所得的试件非局部等效应变分布与量值亦基本一致,这实际上也是试件宏观力学响应基本一致的原因所在.

4 结 语

为实现在ABAQUS平台上基于MAZARS本构模型的混凝土损伤有限元客观分析,本文结合积分形式的非局部理论,给出了非局部MAZARS本构模型的理论表达,并应用非局部等效应变的近似计算方法,提出了与ABAQUS数据传递方式相适应的非局部MAZARS模型数值实现方法.在此基础上,基于ABAQUS提供的UMAT、UEXTERNALDB与USDFLD二次开发接口,通过编制相关程序完成了非局部MAZARS本构模型在ABAQUS平台上的数值实现.算例分析表明,基于MAZARS模型的混凝土损伤有限元分析结果呈现出明显的单元尺寸依赖性,而利用本文所开发的非局部MAZARS本构模型子程序可保证混凝土损伤破坏有限元分析成果的合理性.本文研究成果不仅拓展了ABAQUS在混凝土材料与结构损伤方面的分析功能,亦可为其他非局部本构模型在ABAQUS中的数值实现提供借鉴与参考.