非饱和网纹红土比例加载特性研究

徐有娜，李建中

（1.建设综合勘察研究设计院有限公司，北京100007；2.中南大学地球科学与信息物理学院，湖南长沙410083）

在建造房屋和挡土建筑物的实际工程中，地基土常常位于地下水位以上，并且地基土的加载路径一般都属于比例加载路径［1-2］，并且处于恒应力比路径下的土体大多处于非饱和状态，由于非饱和土体的恒应力比路径的复杂性，国内外有不少学者针对各类土的比例加载特性开展了一系列研究，如Cris-pel J J［3］对不同土样进行了三轴恒应力比例试验，研究表明土的侧向变形在不同的等比压力下的比例关系；孙岳崧等［4］对砂土进行了不同应力路径下的试验，恒应力比试验中其应力-应变关系曲线呈幂函数型，随k值（恒应力比）的增大σ1（轴向应力）-εa（轴向应变）曲线逐渐变陡；钱建固［5］从土体塑性各向异性的微宏观机理上分析，得到在比例加载条件下土体表现为等向硬化和共轴塑性；张宁宁等［6］研究了重塑黄土强度在恒应力比路径下，恒应力比与不同初始固结围压及不同初始含水率的关系。以上研究表明：土体非饱和程度影响土体恒应力比路径应变特征，相关的研究目前还处于基础阶段。因此，本文主要研究的是土在不同饱和程度下的比例加载应力路径的应变特性。

网纹红土是洞庭湖地区常见的土体［7-8］，并且它是一种结构性较强的土，颗粒基本结构单元形状多为片状颗粒和片状集合体，其颗粒之间主要为面-面和面-边接触［9］，具有压缩性较低、孔隙比小、抗剪强度较高的特性，是良好的持力层［10-11］。已有很多学者对网纹红土进行流变特性研究［12-13］，但是对于网纹红土在应力比例加载路径下的特性研究现在都还未涉及。

本文利用应力控制式全自动GDS 静三轴仪对几组含水率相同、干密度相同的重塑网纹红土进行不同基质吸力条件下的恒应力比的三轴固结排水试验，探讨非饱和土网纹红土基质吸力平衡的时间规律，不同恒应力比加载路径下的偏应力和净平均应力、轴向应变和时间、轴向应变与径向应变等关系。

1 试验方案及过程

1.1 试验土样

试验土样为取自湖南省岳麓山脚下的网纹红土，取土深度约3 m，土粒密度为2.71 g/cm3，天然含水率为23.83%～26.88%，天然密度为1.90～1.95g/cm3，天然干密度为1.59～1.75g/cm3。试样的制作按照《土工试验方法标准》（GBT 50123-1999）制备三轴试样的要求制样，并采用真空抽气饱和法对试样进行饱和。试样目标尺寸为61.8 mm×124 mm，参考网纹红土的天然土样的物理力学性质，试验采用的土样的土粒密度为2.71 g/cm3，含水率为22%，土样密度为2.0 g/cm3，初始干密度为1.63 g/cm3。试验过程中，土样的孔隙水压始终为0。

1.2 恒应力比试验

本次试验采用应力控制式全自动GDS 静三轴仪4D 应力路径进行试验。应力控制指径向应力与轴向应力均按一定速率增大，根据工程实际可能出现的情况，每次施加的径向应力与轴向应力的比值即恒应力比k值分别为 0.60、0.63、0.65、0.68、0.70。

1.3 加压标准

将饱和土体施加一级径向应力和轴向应力，待加压时间到目标值后，保持径向应力和轴向应力不变进行固结，待固结稳定后，加一定的基质吸力（20、30、50、60、100、120 kPa），待基质吸力平衡后，加下一级径向应力和轴向应力。该试验采用匀速加载固结方式，加载速率为10 kPa/h。试验过程中，固结围压 σ3取 50、100、150、200 kPa。试验方案见表1。固结稳定标准采用反压体积变化基本保持不变，即取24 h 内排水量＜0.1 cm3的时刻作为固结稳定的标准。在试验过程中尽量保持室内温度不变（20 ℃）。典型试验结果如图1 所示。

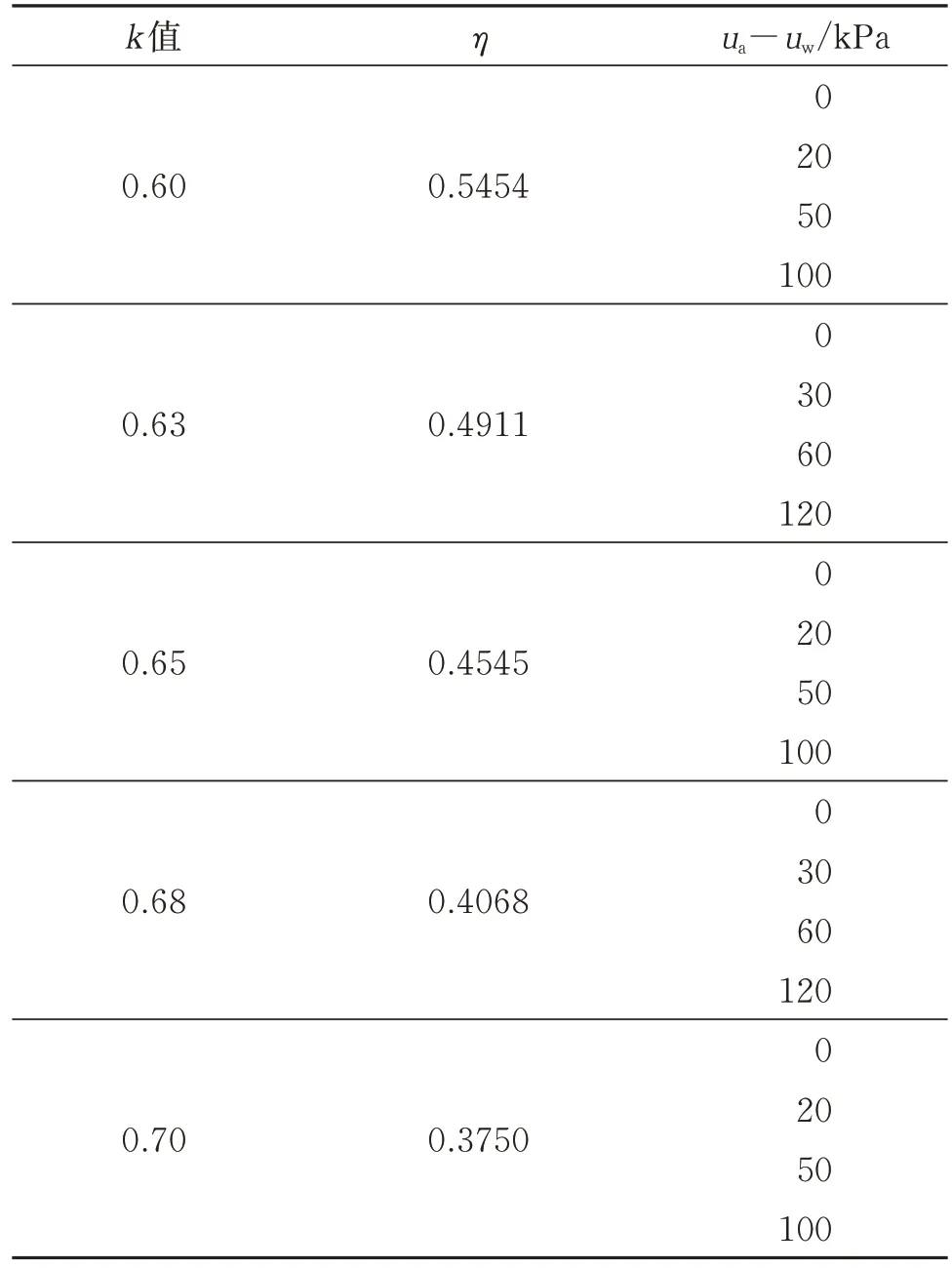
表1 试验方案Table 1 Test plan

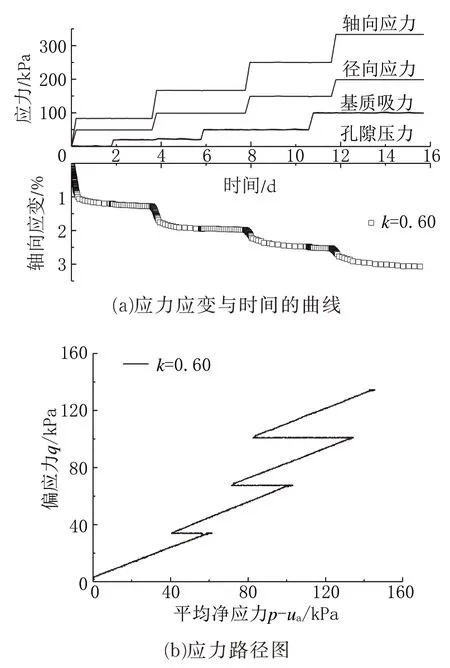
图1 典型试验结果Fig.1 Typical test results

2 试验结果分析

2.1 基质吸力平衡特点

此次试验的基质吸力平衡的标准都采用反压体积变化基本保持不变，即取24 h 内反压排水量小于试样体积的0.05%作为基质吸力达到稳定状态的标准［14-15］。不同试样的不同恒应力比的分级加载试验中各个试样的反压的排水量及对应的基质吸力如图2 所示（仅列出k=0.60 的情况）。

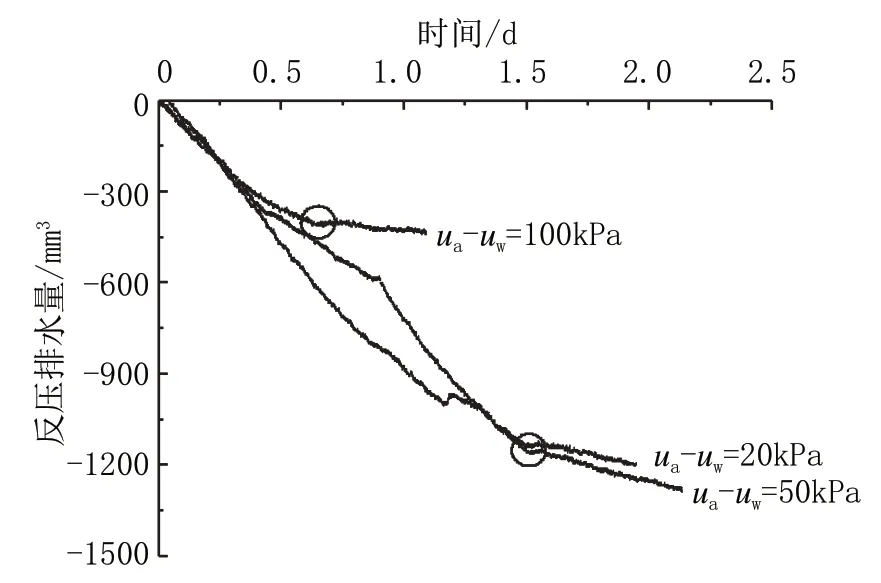
图2 k=0.60 时不同基质吸力的反压排水量与时间的关系Fig.2 Back pressure displacement volume vs time at k=0.60 of matrix suction

从图2 可以看出，随着时间的增加，反压排水量近似成直线增加，但是邻近基质吸力平衡时有一个转折点（如图中的黑色圈部分），可以预示着基质吸力平衡。利用此方法判断基质吸力的平衡时间可以大大缩短。图3 是利用此方法判断出每个基质吸力平衡的时间及对应的基质吸力的散点图，从图中可以看出每个基质吸力的平衡时间不同，但是基本为1.5 d 左右。

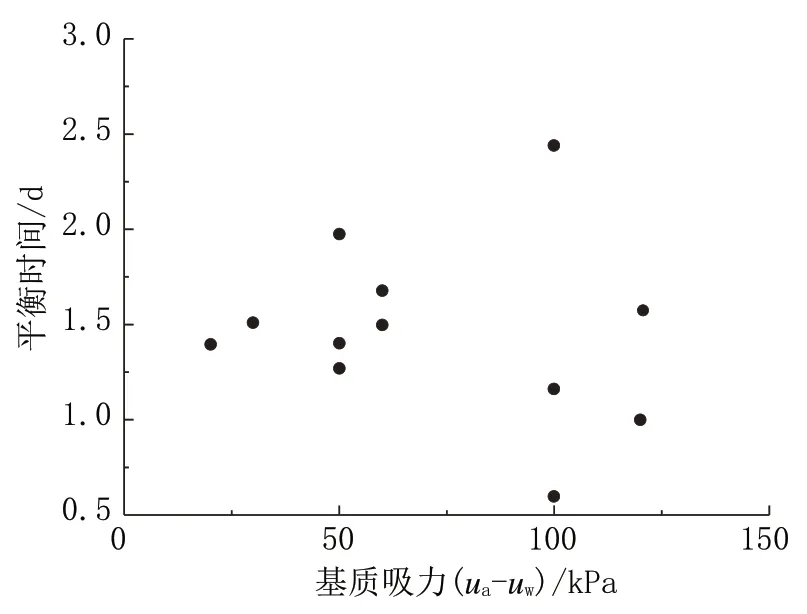
图3 基质吸力和平衡时间的关系Fig.3 Matric suction vs equilibrium time

2.2 基质吸力对不同加载阶段的影响

以前一些学者［16-25］进行了分级加载试验，转换过的每级加载的固结曲线如图4 所示。在本次试验中，将每级不同基质吸力下的轴向应变转换成起始点，前一段为比例加载和固结过程，后一段为加基质吸力和基质吸力平衡过程（见图5）。

从图 5（a）、（c）、（e）中可以看出在基质吸力为50、100 kPa 条件下的加载固结的轴向应变非常接近（与图b、d 相比）。出现本次试验的情况笔者认为应该是受基质吸力的影响。从作用机理上分析，由于加了基质吸力，土体中有了空气，由于空气的可压缩性，此后的固结不仅是随着水的消散的土体的固结，还包括气体的压缩，所以致使以后的固结变形加大。这个结论在实际工程中体现为当地下水水位下降后土体在荷载的作用下变形增加，甚至达到临界状态造成地表坍塌。

2.3 偏应力与净平均应力的关系

图 6 是不同k值下的q-（p-ua）的曲线关系。为了更清楚地反映其中的关系，只选取了k=0.60 和k=0.68 两 个k值 的 曲 线 。

图4 分级加载与转换后分别加载曲线Fig.4 Step-load curves and staged‑load curves converted from step‑load curves

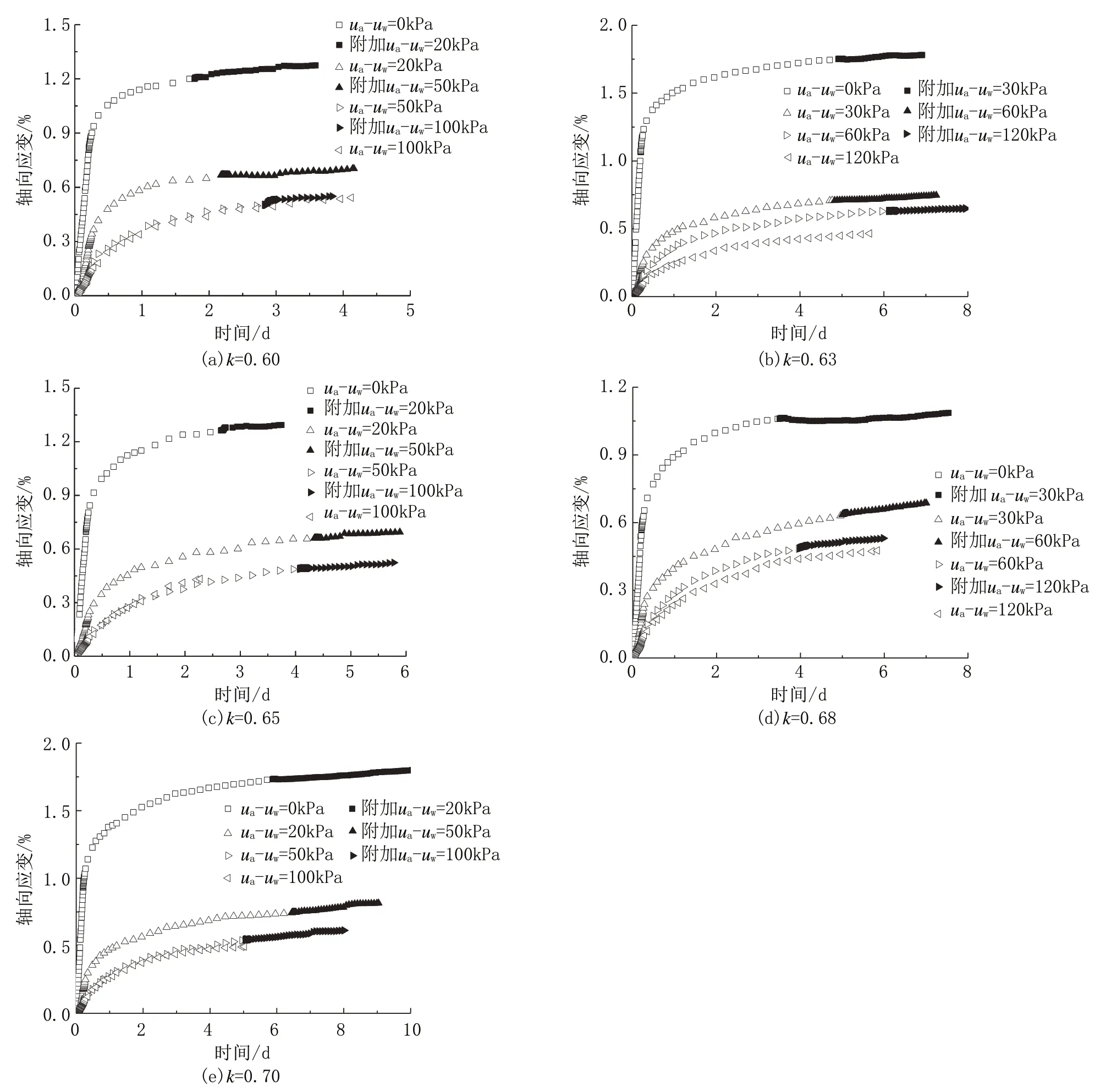
图5 不同基质吸力下的轴向应变与时间的关系Fig.5 Axial strain vs time at different matric suction

图6 不同k 值的偏应力和净平均应力的关系Fig.6 Deviatoric stress vs net mean stress at different k values

结合图1（b）和图6 可以看出，不同基质吸力下偏应力-净平均应力q-（p-ua）呈直线关系。现将其拟合，所有拟合值见表2。

通过拟合可以发现，不同基质吸力下q-（p-ua）成直线，相关系数R2都在0.99 以上，其斜率近似为η恒应力比值，并且有很小的上下波动，直线形式如下式：

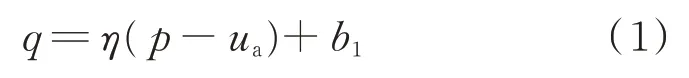
将截距b1和基质吸力（ua-uw）拟合后发现截距和基质吸力成直线关系，如下式：

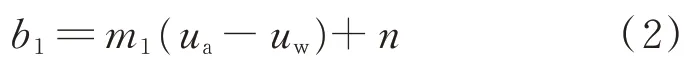
相关系数R2都在0.97 以上，拟合图见图7，拟合数据见表3。

结合公式（1）、（2），可以得出理论上n应该为0，并且拟合出截距n的值为0～2，因此，忽略不计，进而截距b1和基质吸力（ua-uw）的关系简化为：

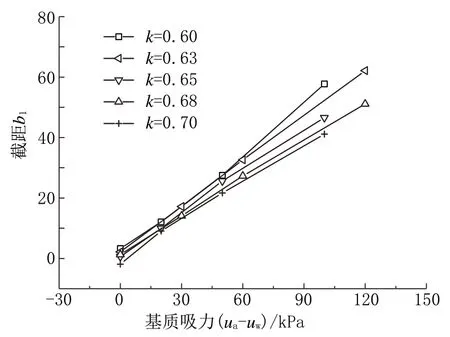
图7 不同k 值的基质吸力与截距的关系Fig.7 Matrix suction vs intercept at different k values

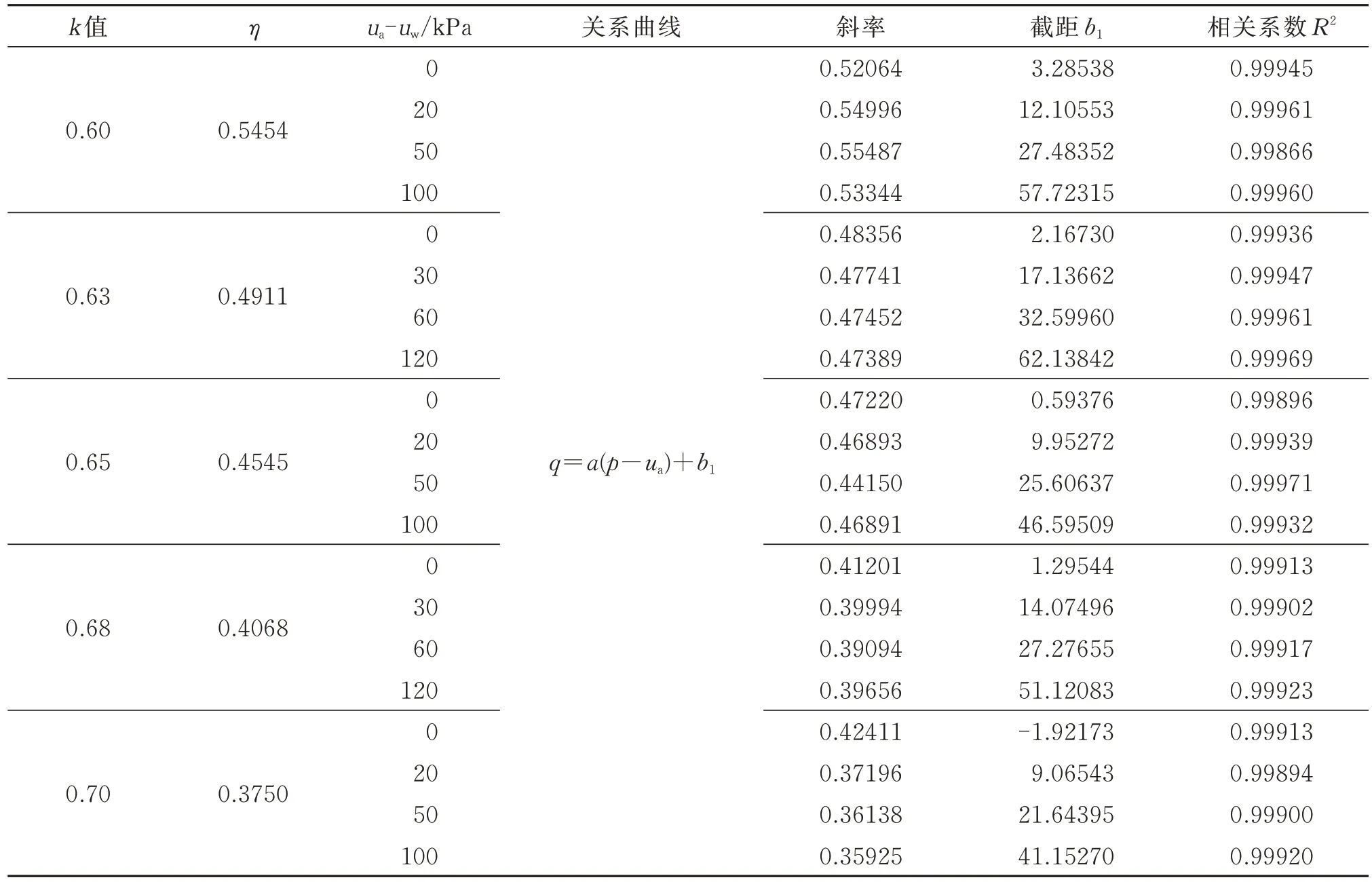
表2 所有拟合值和相关系数Table 2 Fitting values and correlation coefficients

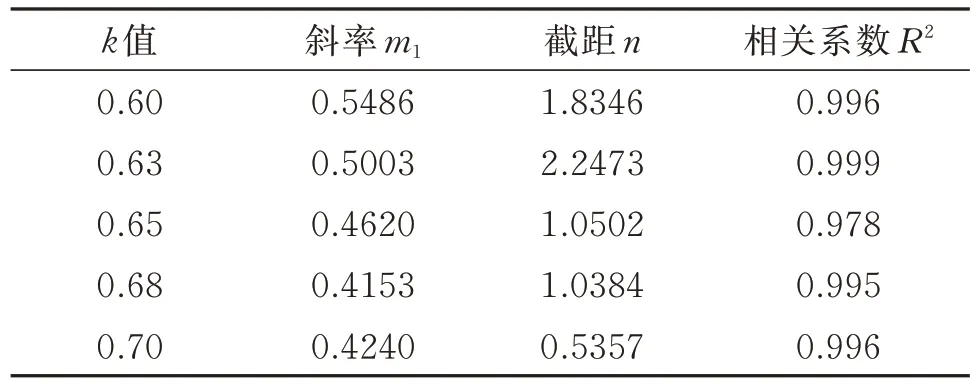
表3 截距和基质吸力拟合值Table 3 Fitting values between intercept and matrix suction

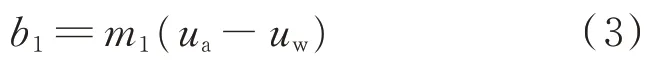
将斜率m1与k值拟合呈直线关系，如下式：

其 相 关 系 数 为R2=0.9328，a=-1.3499，c=1.3502（参见图 8）。

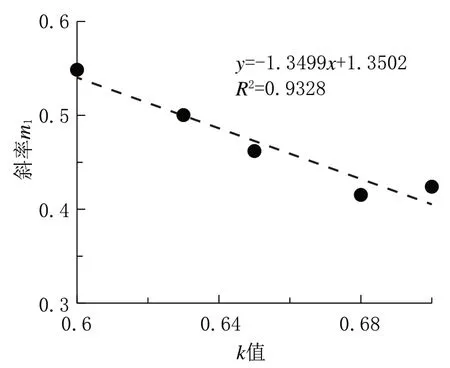
图8 不同k 值的基质吸力与斜率的关系Fig.8 Matric suction vs slope at different k values

结合公式（2）、（3）、（4）可得出偏应力与净平均应力、基质吸力、k值的关系：

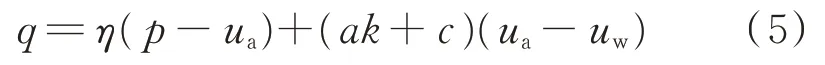
综上所述，不同k值、不同基质吸力下的等比例加载条件下的偏应力-平均有效应力q-（p-ua）成直线关系，关系式为式（1）。而偏应力与净平均应力、基质吸力、k值关系如式（5）。

2.4 轴向应变与径向应变之间的关系

不同k值、不同基质吸力下固结阶段的轴向应变与径向应变的关系如图9 所示（选2 个典型曲线）。

从图9 中可以看出，轴向应变与径向应变近似成直线关系。现将其拟合呈线性，如式（6），所有拟合值见表4：

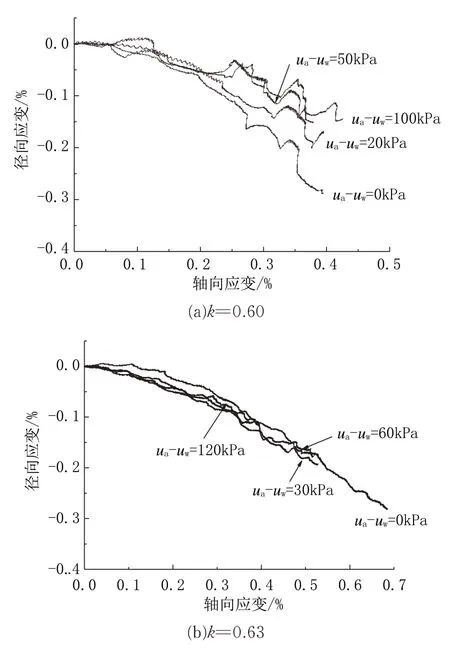
图9 不同k 值的轴向应变与径向应变的关系Fig.9 Axial strain vs radial strain at different k values

如果忽略掉网纹红土的瞬时变形（即土的变形都是由固结与蠕变产生），则式（6）中的b2=0，则式（6）可以转变成：

现将基质吸力和斜率m2拟合，结果发现呈抛物线形式，如式（8）：

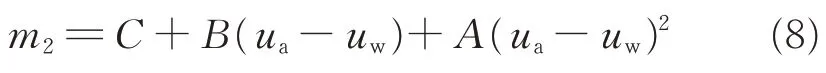
典型拟合曲线见图10（选1 个典型曲线）。

根据拟合出抛物线曲线数值计算出对称轴值-B/（2A）（如表 5 所示）。

拟合k=0.60、0.65、0.70 的抛物线的对称轴和k值成直线关系，如下式：

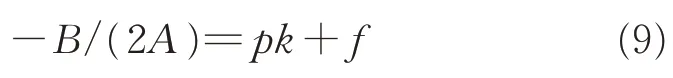
拟合曲线如图11 所示。

结合式（7）、（8）、（9）可以得出径向应变和轴向应变，k值与基质吸力的关系，从而能预测径向应变。

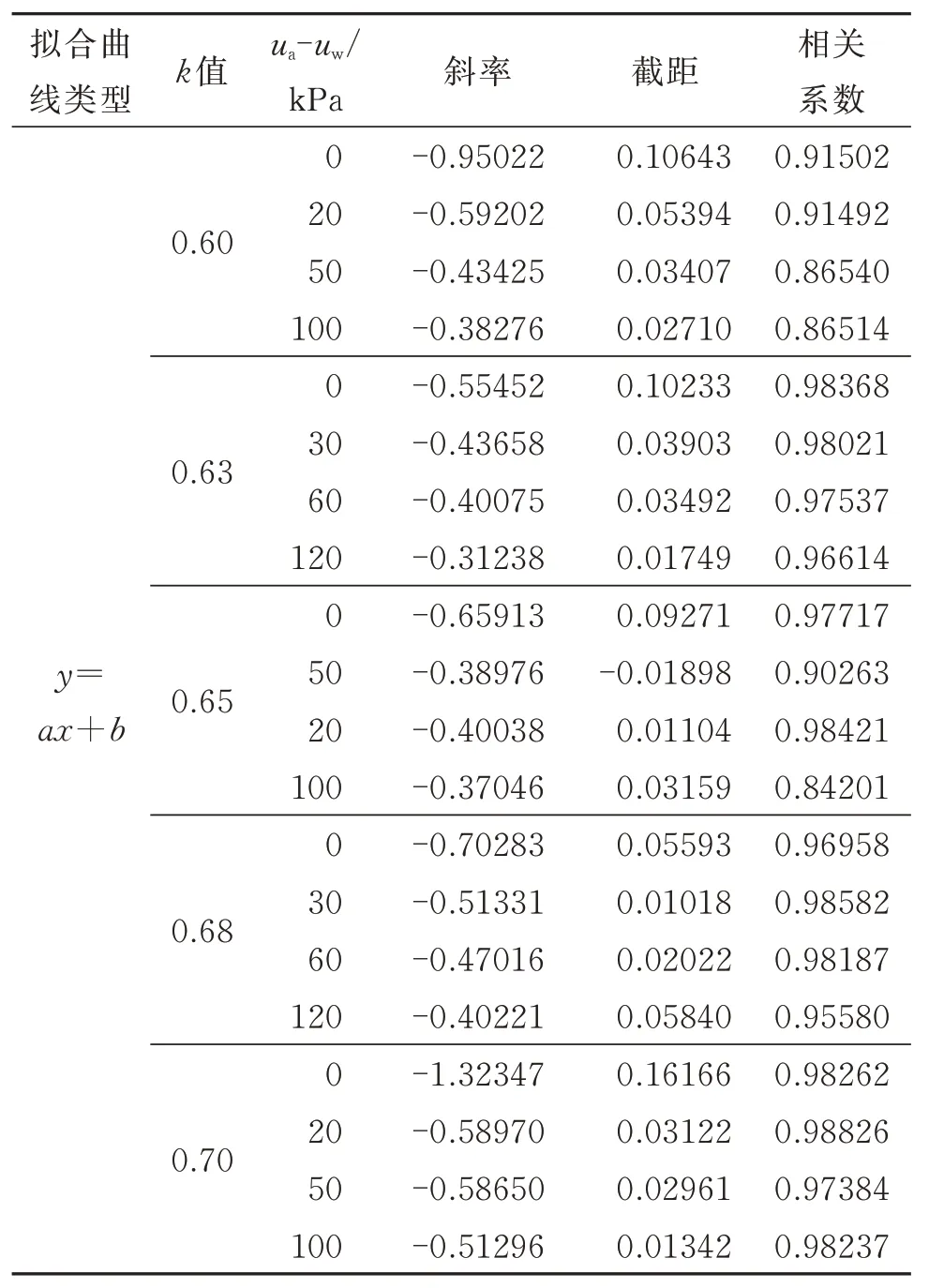
表4 线性拟合值Table 4 Linear fitting values

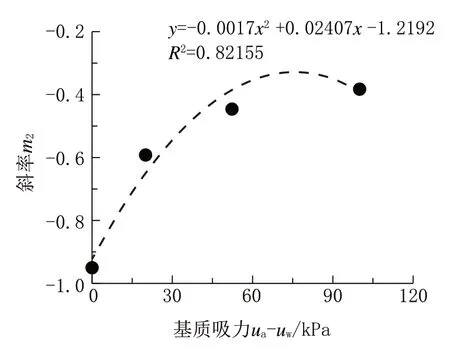
图10 斜率m2 和基质吸力的值以及拟合曲线Fig.10 Slope“m2”,the values of the matrix suction and the fitting curves at different k values

表5 对称轴值与k 值Table 5 Values of the symmetric axis and the k values

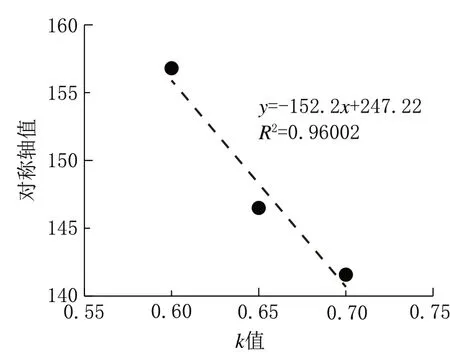
图11 k 值与对称轴的关系Fig.11 k value vs symmetric axis

3 结论

（1）在比例加载条件下的基质吸力平衡过程中，反压排水量有一个明显的转折点，通过转折点判断基质吸力的平衡可以大大缩短时间。

（2）基质吸力作用会“加深”变形，这主要受基质吸力的影响。从作用机理上分析，由于加了基质吸力，土体中有了空气，由于空气的可压缩性，此后的固结就包括气体的压缩，所以致使以后的固结变形加大。这个结论在实际工程中体现为当地下水水位下降后土体在荷载的作用下变形增加，甚至达到临界状态造成地表坍塌。

（3）经分析得出在保持偏应力不变的前提下，增加基质吸力没有引起明显的轴向应变增加；不同基质吸力下的偏应力和净平均应力呈直线关系，其斜率近似为恒应力比。

（4）提出了一种可以预测非饱和比例加载条件下的径向应变的方法。