基于阿波罗尼斯圆背景下的高考数学

张丽群

(福建省莆田擢英中学 351100)

一、试题展示

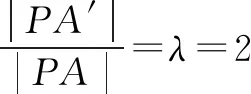
二、设计过程

1.命题意图

阿氏圆这样经典的数学文化课题的研究，渗透现代数学思想方法.本题考查对阿氏圆数学文化的理解，也考查曲线与方程，抛物线动点中线段和差求最值问题.此题设计旨在体现(普通高中数学课程标准)修订中对数学文化的考查.考查推理论证能力、逻辑推理能力、运算求解能力，考查数形结合思想、转化化归思想，考查直观想象、数学抽象、逻辑推理、数学运算、数据分析等核心素养.体现了基础性、综合性、应用性、创新性等.

表1 学科核心素养的表现及其级别

2.命题过程

本题的选材主要参考四个部分的内容：

第一部分：新课标《人教版·必修2》在第四章平面解析几何初步,第4.1节圆与方程介绍了圆的标准方程和一般方程基础知识后，在第131页习题4.1B组第3题(2).

第二部分：2013年江苏卷17题.

原题2 在平面直角坐标系xOy中，点A(0,3)，直线l：y=2x-4.设圆C的半径为1，圆心在l上.

(1)若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；

(2)若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

第三部分：2017年普通高等学校招生全国统一考试Ⅰ卷理科数学第10题.

原题3 已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1,l2，直线l1与C交于A,B两点，直线l2与C交于D,E两点，则|AB|+|DE|的最小值为( ).

A.16 B.14 C.12 D.10

第四部分：各省市质检卷.

三、解答分析

1.考点分析

解析几何，数学文化，隐形圆，线段和、差最值.

2.解法呈现

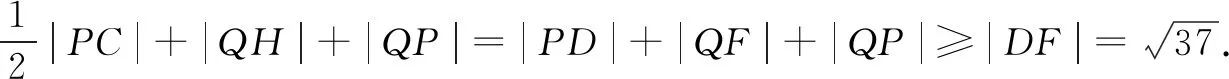
当D,F,P,Q四点共线时取得最小值.

解法2(1)同解法1;

(2)设(x+3)2+y2=4的圆心为K(-3,0),半径r=2.

连接KP,PD,PC,r=KP=2,且KC=4，D(-3,1).

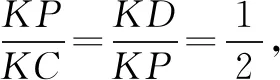
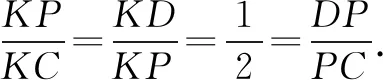
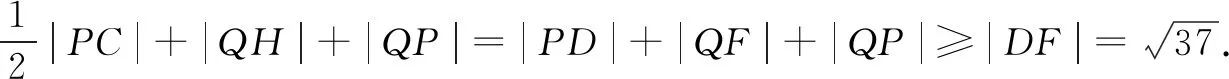
四、试题评析

本题的核心知识点是在阿氏圆的背景下运用其性质，与常规的抛物线动点求线段和差最值问题相结合得到的创新题.本题参考原题的出题方式：题型可为填空题，也可分解为解答题，本次设计为填空题，重点考查平面解析几何相关内容.结合课程标准，圆锥曲线高考题以椭圆、抛物线为模型展开，并结合其他平面几何知识，以圆，三角形，四边形为载体进行拓展.因此，保留(1)(2)(3)原题中的模型框架，对其他的条件进行强化、延伸.本试题的后续改编将侧重于题根题源的总结，改编的立意主题仍然是考查圆锥曲线的基本定义，保证改编试题不脱离高中数学课程标准.

五、命题拓展

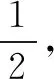
方案1问题延伸(求定比λ).

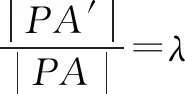
方案2问题延伸(求另一定点).

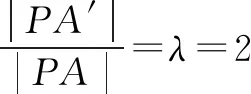
方案3问题延伸(求两个定点).

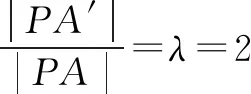
方案4问题延伸(求定点和定比).

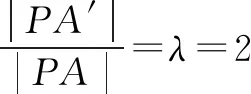
方案5问题延伸(阿氏圆与椭圆双曲线+三角形面积的结合).

六、命题反思

通过解读(2017年版高中数学课程标准)，深刻领悟到高考评价体系中对数学考查内容的“基础性、综合性、应用性、创新性”的定位.要结合教材内容对数学文化这一概念认真学习，特别是对教材中渗透的数学文化内容要充分重视，重点研究；结合近年新课标试题中出现的与数学文化有关的试题进行学习，重点关注题源、考法命题形式.