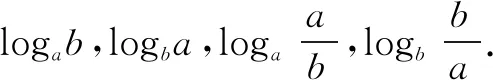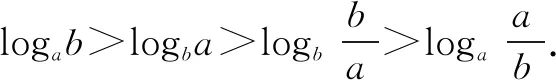巧用函数的单调性比较大小
2021-02-02张岭芝
张岭芝
(江苏省无锡市青山高级中学 214036)
利用幂函数、指数函数、对数函数等基本初等函数比较两个或多个函数值的大小是高一代数的一个热点,也是一个重点,有没有象乘法口诀“三五十五”那样朗朗上口且通俗易懂的方法来比较函数值的大小呢?有!笔者经过多年的教学,总结出“大大大,大小小,小大小,小小大”这四句口诀.
一、同底数幂的大小比较
同底数幂的大小比较是利用指数函数y=ax(a>0且a≠1),当a>1时,在R上单调递增,当0 例1比较下列两组数的大小: 同底数对数的大小比较是利用对数函数y=logax(a>0,a≠1)当a>1时,在R*上单调递增,当0 例2比较下列各组数的大小: 同指数幂的比较的是通过幂函数y=xα当α>0时,在R*上单调递增,当α<0时,在R*上单调递减这个性质来进行比较的. 例3比较下列两组数的大小. 注意:四句口诀中“大”的个数不是3就是1,相应的“小”的个数不是0就是2! 事实上,口诀“大大大”本应该是下面的三句:增大大(增函数+自变量大⟹函数值大),大增大(自变量大+增函数⟹函数值大),大大增(自变量大+函数值大⟹增函数,注:此处仅研究单调函数),就是说,“大大大”中的一个“大”应该是“增”,只不过用“增”字,口诀就变成三句了. 同理对于另外三句:“大小小,小大小,小小大”,把其中的一个“大”改为“增”,或者一个“小”改为“减”,比如“减大小(减函数+自变量大⟹函数值小)”当然是成立的.如果这样一改,三句口诀就变成九句了,为了简约又朗朗上口,还是“大大大,大小小,小大小,小小大”这四句口诀比较好,实践证明用这四句口诀比较两个函数值的大小特别顺,效果特别好. 练习1若0 解析由“大大大”知,xa>ya>1a=1(此处用幂函数单调性比较),由“小大小”知,ax 所以xa>ya>ay>ax. 事实上,这种情况可以推广到更一般初等函数. 例4比较下列两组数的大小: 口诀“大大大,大小小,小大小,小小大”没有多少科技含量,也没有什么噱头,就是一个实用工具而已,学生如果能记住并用好就是作者最大的心愿.
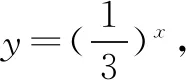
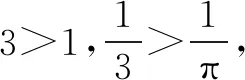

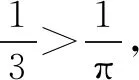

二、同底数对数的大小比较




三、同指数幂的大小比较

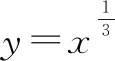
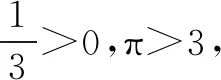
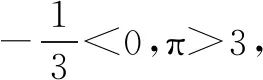
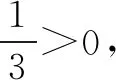
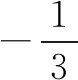
四、应用举例