如何解答高考解析几何压轴题

龚东传

(广西壮族自治区南宁市武鸣高级中学 530199)

高考解析几何压轴题对学生分析问题以及运算能力要求较高.部分习题具有一定的技巧性，难度较大.为使学生掌握相关的解题思路，讲解相关例题时应注重与学生互动，更好地加深学生印象，提升学生的学习体验.同时，注重在课堂上留下空白时间，要求学生相互交流经验，总结解题思路，在以后解题中少走弯路.

一、过定点问题

学生对解析几何中的定点问题并不陌生.解答该类问题应认真审题，巧妙地设出相关参数，尤其应充分挖掘题干中的隐含条件，将其转化为对应的数学表达式，构建出参数之间的关系进行求解.

(1)求椭圆C的方程；

(2)证明直线MN过定点.

该题目中的问题(1)难度不大，而问题(2)难度较大.审题时，应由“∠MAN的平分线在y轴上”明确直线AM，AN的斜率之和为零.设出直线方程y=kx+m以及M，N两点坐标，通过联立直线方程与椭圆方程，分别表示出两条直线的斜率，求出m的值，其过哪个定点便一目了然.

二、取值范围问题

高考解析几何压轴题求解参数取值范围常用的知识点有函数、基本不等式.成功求解出相关函数以及不等式成为解题的关键.同时，还应找到相关参数的取值范围，一般可通过椭圆的有界性、直线与椭圆方程联立后根的判别式的值获得.

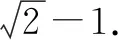
(1)求椭圆的标准方程；

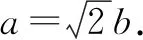
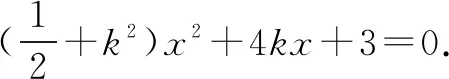
B板块作为本次中国汽车后市场店面运营综合解决方案展的一大亮点，开设“TOP20维修工具评选上榜产品”专区，集中展示了《汽车维修与保养》杂志评选出的2017年度“20佳”维修工具20款、2017年度维修工具优秀产品20款。“20佳”维修工具评选由国内50多位业内专家评选出的，是中国汽车后市场最具影响力的专业评选活动之一，至今已有14年历史，多年以来以其“公开、公平、公正”的评选原则和“创新、实用、高效”的评选宗旨得到了国内汽车后市场业内人士的普遍认可和推崇。本次“TOP20维修工具评选上榜产品”的集中展示在现场获得了参展专业观众和专业买家的一致好评。

设M(x1，y1)，N(x2，y2)，由韦达定理，得

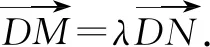
即x1=λx2.所以x1x2=λx22，x1+x2=(1+λ)x2.

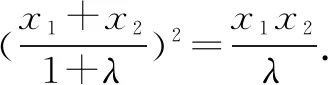
三、面积问题

解答高考解析几何压轴题中的面积问题时，应根据图形形状，寻找对应的面积表达式.如果是三角形可运用点到直线的距离、正余弦定理进行求解；对于四边形则常将其划分成三角形，或运用其对角线的垂直关系进行求解.

(1)求椭圆的标准方程；

(2)求四边形ACBD面积的取值范围.

分析该题目的两个问题难度均较大.问题(1)需要通过添加辅助线先求解椭圆离心率，找到a，b，c之间的关系.问题(2)由问题(1)可求出直线l1的方程，易知直线l1和l2垂直，因此，四边形的面积不难表示出来.将直线l1与椭圆方程联立，可求出A，B两点坐标以及长度.解题关键在于求出CD的长，根据经验设出其方程为y=-x+m，通过联立直线l2和椭圆方程，再运用韦达定理便可求出CD的长.由“直线l2和线段AB交于点P”可求出m的取值范围.

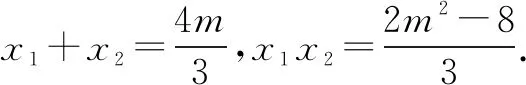
高考解析几何压轴题解题较为灵活，授课中应根据高考常考题型，为学生逐一讲解相关例题，并组织学生加强训练，使学生能够通法通解，积累相关的解题经验，总结相关题型的解题思路，为其以后更好地解题提供良好指引.