试论高中数学例题解答中导数的典型性应用

傅泽平

(湖南省长沙市长沙大学附属中学 410003)

一、理解导数概念，了解例题有关思路

1.理解导数性质，解答导数例题

2.多做有关导数的题目，加深例题思路的印象

在学习过程中，要多做有关于导数的数学题目，不断地通过例题练习和思路分析来加深对导数概念的掌握和导数知识点的应用，也为解决数学问题提供新的解题思路.所谓俗话说“熟能生巧”，在学习过程中多做练习题对于加深导数问题的应用具有重要的作用，同时知道导数对学习数学知识的重要性.例如已知函数y=x-a·lnx，求函数的极值.这种题目属于带参数的函数极值问题，解题时我们需要考虑参数的取值对函数极值的影响.

解题步骤：

(1)先确定函数的定义域，当a≠0时,x∈(-,0)∪(0,+),当a=0时,x∈R；

(3)讨论a的不同取值对y极值的影响：当a>0时，在x∈(-,0)和(a,+)时，导函数y′>0,函数单调递增，在x∈(0,a)时，导函数y′<0，函数单调递减，此时函数在x=a处取得极小值；当a=0时，函数在x∈R单调递增，不存在极值；当a<0时，在x∈(-,a)和(0,+),导函数y′>0，函数单调递增，在x∈(a,0)时，导函数y′<0，函数单调递减,函数在x=a处取得极大值.

通过对这个例题的分析，我们可以总结得到，对于含有参数的函数极值问题，首先需要考虑参数对于函数的定义域的影响，讨论不同情况下函数的定义域，然后再对函数进行求导，通过导函数得到函数在定义域的单调性情况，最后讨论不同参数的取值对于函数极值的影响.

二、高中数学例题解答中导数的典型性应用

下文中将具体地从不同的数学习题中来分析导数在解答数学典型例题中的应用.

1.导数在求解最值中的应用

导数在高中数学中具有重点教学意义，高中数学习题经常通过导数和最值问题的联系来考查学生对综合数学知识和知识系统的总结能力，所以学生在数学学习过程中，必须掌握导数在求解最值问题中的应用.对于可导的函数来说，导数是判断函数单调性的最有力工具，因此在求解函数最值的过程中，利用导数知识分析最值问题既方便又高效，所以利用导数求解最值问题就变成了最简单自然，并且有效的方法.下面以一个高考数学习题为例.

例1已知函数F(x)=x3-3x+1，求这个函数在[-3,0]上的最大值和最小值.

这一类的问题是导数解决最值问题中最基础的一个题目，它的解题思路就是首先要了解在题目中所提供的闭区间上函数的极值，其次利用端点函数值来进行比较大小进而确定最值问题.

解题步骤：

(1)首先对F(x)进行求导，得到F′(x)=3x2-3；

(2)令F′(x)=0，求得导函数的零点值为x=±1，此时我们可以知道,当x∈[-3,-1)时,F′(x)>0，所以F(x)在[-3,-1)单调递增；当x∈(-1,0]时,F′(x)<0，所以F(x)在(-1,0]单调递减.我们可以得出，F(x)在x=-1处取得最大值F(-1)=3；

(3)F(x)取得最小值的点应该是区间[-3,0]的端点处，将x=-3和x=0代入函数F(x),得到函数值分别为F(-3)=-17和F(0)=1，最后进行比较，得出F(x)的最小值为F(-3)=-17.

通过对这个例题的分析，我们可以总结得到，在解答最值问题过程中利用导数的相关知识，首先需要在函数的区间范围内求出极值；第二是求出函数在端点的函数值，也就是自变量区间两个端点处的函数值；第三就是将极值点和端点的函数值比较大小，以此来求出函数的最值.

2.利用导数来解决曲线的切线问题

在高中数学学习过程中，我们经常会遇到这样一个题目，那就是在坐标系中求解有关切线方程的问题.通常情况下，我们会得知在曲线外的一个坐标点，然后求解此点的切线方程.对于这类题目来说，如果学生单凭作图或者运用函数的基本概念进行解答很难将题目正确地完成，所以在解答过程中引入导数的相关内容可以更加有效地解答此类题目.

例2 已知曲线C：y=F(x)，求经过点P(x0，y0)的曲线切线方程.

如何利用导数知识来更加准确地解决此类题目呢？在实际解题过程中，我们先要确定点是否在对应的曲线C上，然后再将y的导函数求出，进而通过计算得到答案.在此过程中，我们一定要掌握在不同情况下的函数所具有的不同结果，分情况进行讨论得到最完整的答案.

解题步骤：

(1)当点P(x0，y0)在曲线上时，先求F(x)在P(x0，y0)处导数值F′(x0),则可以得到切线方程为y-y0=F′(x0)(x-x0);

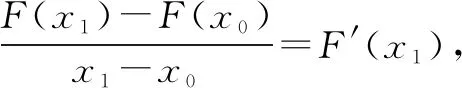
在高中阶段数学学习过程中，我们经常会碰到对特殊曲线求解切线方程的问题，例如三角形曲线，如果利用传统的解答切线问题的方法，画图过程将非常复杂，同时也非常容易出现错误，因此学生在解答此类题目时引入导数知识也是对函数值问题的进一步扩展.

3.运用导数解答三角函数问题

利用导数来解决三角函数问题，例如求函数y=(1+cos2x)2关于x的导函数，这个题目是比较典型的函数求导题.在解答此类题目中，学生可能会由于不熟悉复合函数求导公式而出现错误，所以在当次数相同的2x与x之间，其为一种复合过程，所以在实际解答此类题目过程中，学生要尤其注意这一点，避免在解答过程中出错.所以在解答此类题目中，可以代入第三个函数，以此来进行解答.

解题步骤：

(1)y=u2，u=1+cos2x.

对于导数学习需要学生掌握基本的导数概念，并学会利用导数在数学习题过程中的使用原则.学好导数不仅仅可以使学生能够更好地解答数学题目，还能够在生活中将数学知识得以应用.导数实质也是一种函数的存在形式，并且也是曲线上任意一点的斜率，通过利用导数的数学含义，使得导数只是在解决切线问题过程中具有更加有力的价值，使得解题思路进一步扩展，解题过程变得更加简单，解决问题变得更加高效，使学生能够快速掌握数学知识，并且得到更加明确的解题思路.