向量的一个简单结论及其应用

张兵源

(福建省漳州市教育科学研究院 363000)

一、结论与证明

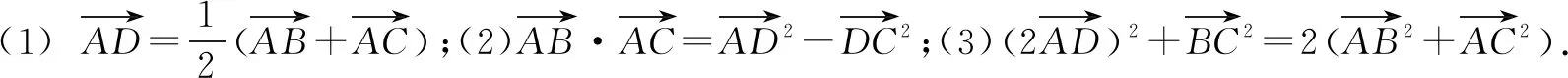
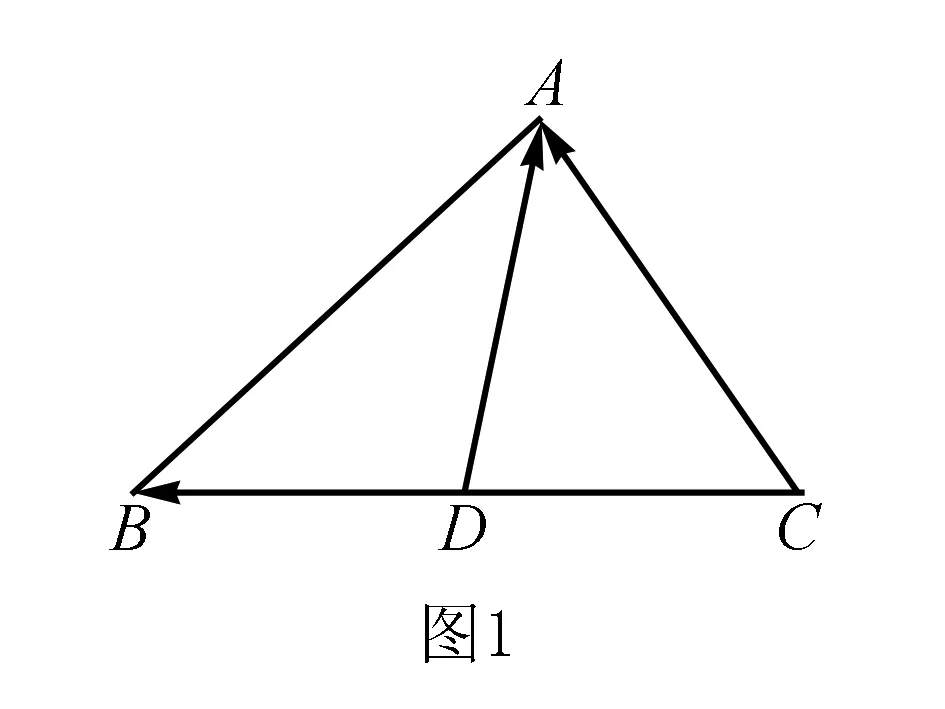
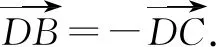
上述证明的实质是向量加法运算与减法运算的互换.向量的减法运算是定义在向量加法运算基础上的,即a-b=a+(-b).换言之，向量的加法运算也可以转化成减法运算,即a+b=a-(-b).这些看似简单的转化,其实能够起到巨大的作用,成为解题的关键,可谓四两拨千斤.

二、结论应用

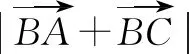
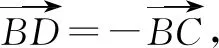
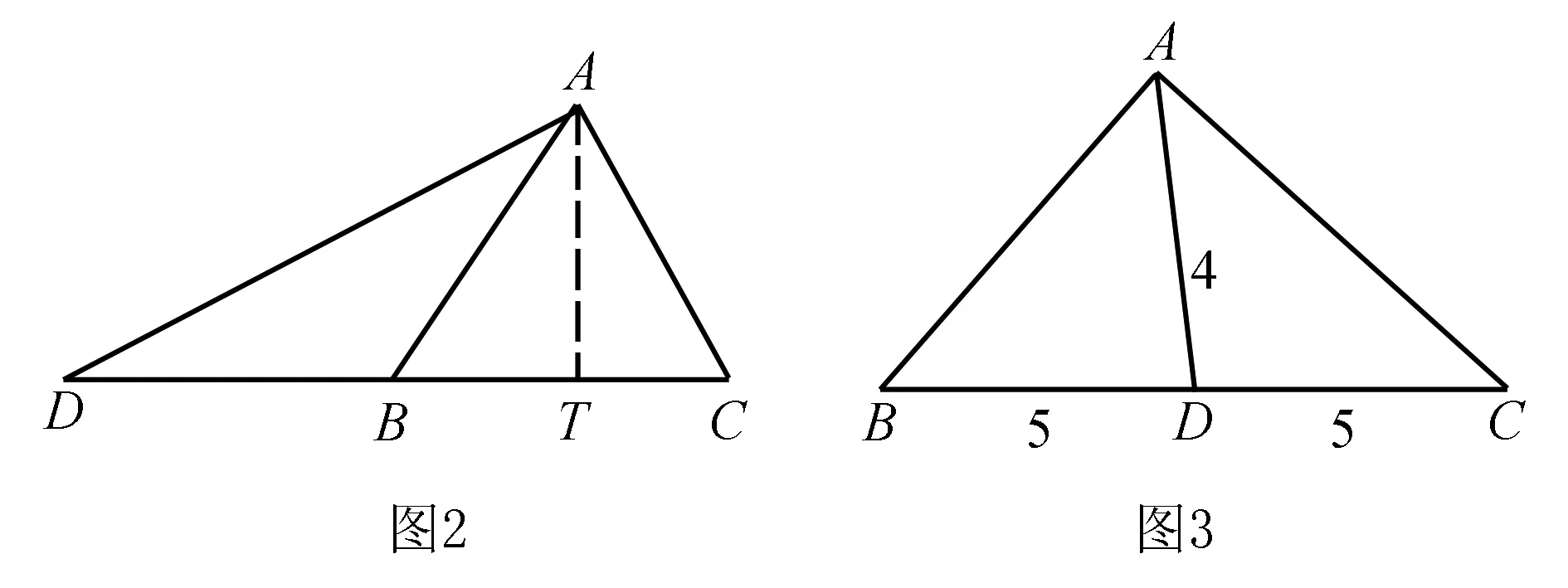
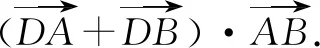
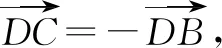
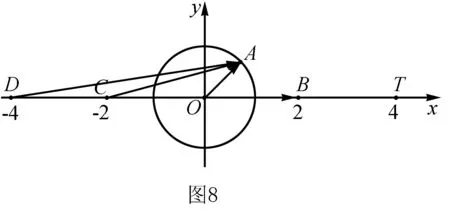
例3已知|a|=1,b满足|a-b|+|a+b|=4,则|b|的最小值为____.

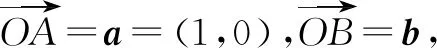
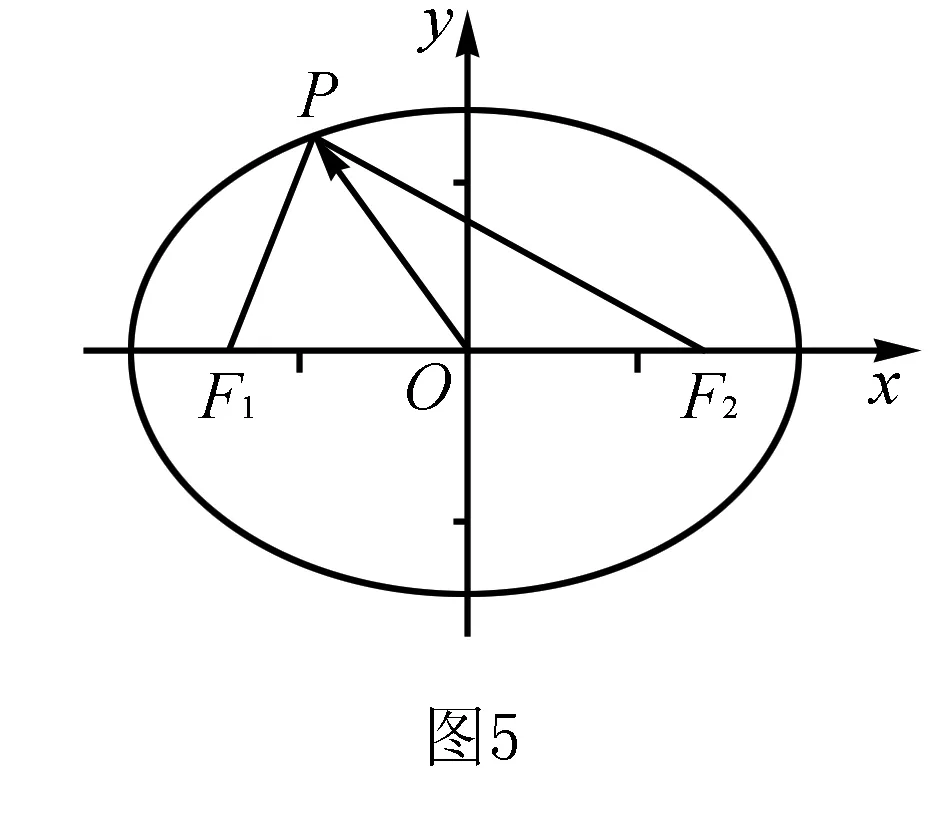
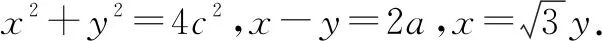
例6已知|a|=1,|b|=2,求|a+b|+|a-b|的最值.

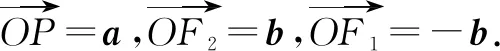
例7已知|a|=1,|b|=2,求|a+b|+|a+2b|的最值.

三、变式练习

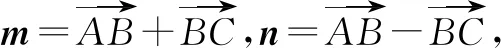
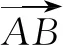
由已知可得平行四边形ABCD为矩形,所以△ABC的形状为直角三角形,且∠B为直角.

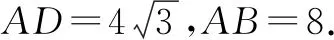
练习3已知|a|=1,|b|=2,求|a+b|+|2a+3b|的最值.

当A位于(1,0)处时,有最大值11,当A位于(-1,0)处时,有最小值5.

练习4已知|a+2b|=3,|2a+3b|=4,求a·b的最小值.

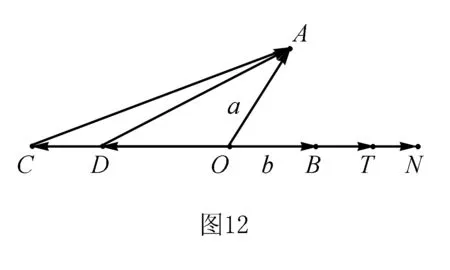
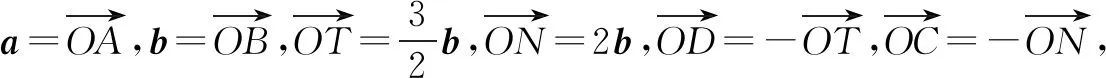
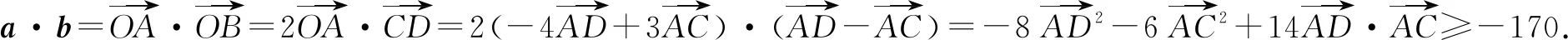
所以a·b的最小值为-170.

不难发现,通过构造相反向量,向量的加法运算可以转化成向量的减法运算.这样的思维其实是逆向思维,是建立在对课本概念的深刻理解之上.由此可见,解题要建立在对课本概念、定理、性质的深刻理解之上,唯有如此才能真正地提高思维,提高能力,促进深度学习,提高数学核心素养.