排列组合中的围坐圆桌问题

武增明

(云南省玉溪第一中学 653100)

排列和组合一直是高中数学的一个重要内容，一直是高中数学教与学的一个难点，一直是高考的一个热点.在排列组合问题中，有一类围坐圆桌问题，许多学生感到很难求解、很难理解求解思路、很难看懂解答过程.究其原因，笔者认为关键是教者没有讲深、讲透、讲清楚、讲明白排列的定义，学者没有理解深、理解透排列的定义.下面试举几例，权作抛砖引玉之用，旨在希望能帮助读者突破学习难关.

一、围坐圆桌不限制问题

例1 10名同学围成一个圆圈唱歌，有多少种不同的围站方法？

解析当10个人围成一圈时，每个人都以顺时针(或逆时针)方向转动一个位置得到的排列与原排列只能算一种排列；于是再依同方向连续转2，3，4，…，9个位置得到的排列与原排列也只能算一种排列，因此10个人围成一圈的一种排列在普通的排列(也称直线排列)中就是10种，所求的排列数是10个人排成直线排列的十分之一.

此题的解析和评注，笔者认为说得很清楚了，但是，仍然有许多学生看不懂、不理解.下面我们再来看一个例子.

例2 若一张圆桌有3个座位，现安排3个学生去坐，每人坐一个座位，有几种不同的入座方法？

解析我们先看排列的定义，一般地，从n个不同元素中取出m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列.

下面我们先用列举法解答此题.用A，B，C表示这3个人，用圆圈表示3个座位，如图1中的图(1)至图(6)，我们从顺时针方向来看(从逆时针方向来看也可以)，图(1)、图(2)、图(3)入座的顺序都没有变，都是ABC，所以由排列的定义知，图(1)、图(2)、图(3)是同一种排列，也就是同一种入座方法.同理，图(4)、图(5)、图(6)是同一种入座方法.于是所求有2种不同的入座方法.

二、围坐圆桌相邻问题

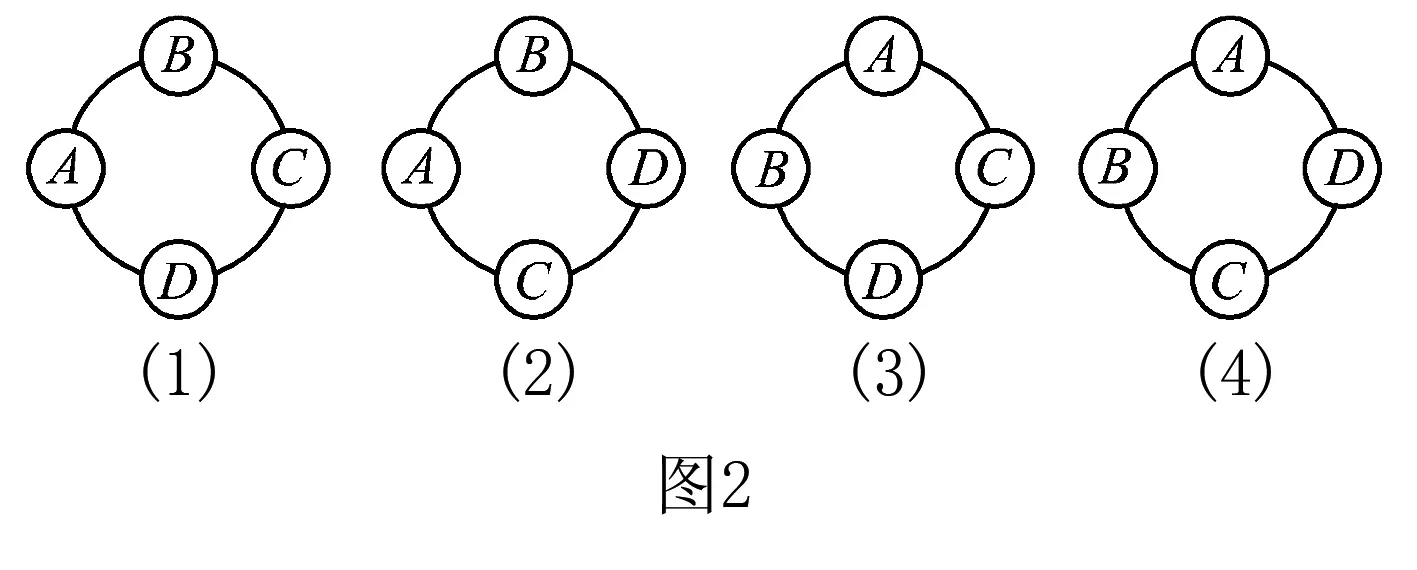
例3A，B，C，D四人围着一张圆桌就坐，如果A，B二人相邻，有多少种不同的入座方法？

三、围坐圆桌不相邻问题

例4 (2018年北京大学博雅计划自主招生考试题)15个人围坐在圆桌旁，从中任取4人，他们两两互不相邻的概率是( ).

例5 一圆形餐桌依次有A，B，C，D，E，F共6个座位.现让3个大人和3个小孩入座进餐，要求任何两个小孩都不能坐在一起，则不同的入座方法总数为( ).

A. 12 B. 36 C. 72 D. 144

解析注意到这里的座位不同，应分两类入座.

四、珠子穿成手镯问题

例6 6颗颜色不同的钻石，可穿成几种钻石圈？

解析这是6个人围坐圆桌问题，同时还要考虑“钻石圈”可以翻转.