汽车声学包轻量化设计*

唐中华，贺岩松，马 涛，张志飞，蒲弘杰，李 云，陈 钊

（1.重庆大学汽车工程学院，重庆 400044；2.东风柳州汽车有限公司，柳州 545005）

前言

车内噪声按照频率可分为低频、中频和高频噪声。车内低频噪声可采用有限元法和边界元法等分析求解［1-2］；而随着频率的升高，车身结构在高频段呈现出“短波长、高模态密度和高模态重叠数”［3］等特性，导致有限元法不适用于高频噪声分析；而统计能量法（statistical energy analysis，SEA）可克服这些不适合有限元分析的因素［4］，故可广泛应用于高频噪声研究中［5-8］。Dejong［5］首次尝试采用统计能量法预测车内噪声问题，建立了包含34 个子系统和考虑动力总成、路面和风等3 种激励的整车模型。陈书明等［7］基于统计能量分析原理，建立了47 个车身结构和车外声腔子系统，成功地预测了汽车车外噪声。刘加利等［8］利用统计能量法深入研究了高速列车车内气动噪声的频谱特性和速度依赖性等规律。

声学包是控制车内高频噪声的有效措施［9-11］，将不同吸、隔声材料进行最优组合，不仅可获得良好的声学性能，还能实现材料的轻量化［12］。吴宪等［11］以覆盖率、堵件厚度、PU 泡沫厚度和EVA 面密度为设计变量，对前围板声学包进行优化，使声学包在隔声性能与质量之间取得最佳平衡。杨晓涛等［13］采用NSGA-Ⅱ遗传算法对顶棚声学包Kriging 近似模型进行优化，得到了顶棚4 层吸声材料的最优组合，兼顾了降噪与轻量化性能。而运用统计能量法搭建整车模型，从整车声压和轻量化角度对声学包进行优化，不仅能获得最佳声学包组合，还可以有效降低整车开发成本和缩短开发周期。

为指导车内声学包的优化，运用统计能量法建立整车模型并计算驾驶员头部声腔声压，与试验值对比验证模型的准确性。根据各子系统对驾驶员头部声腔声压的贡献量分析，进而提出内前围和地板子系统声学包改进方案。最后，面向车辆的总声压级和总质量建立Kriging 近似模型，采用多目标遗传算法对声学包材料厚度进行优化，实现声学包优化设计。

1 SEA整车模型

1.1 SEA基本原理

统计能量法从统计角度出发，将复杂系统分解为多个便于独立分析的子系统，并用经过空间和频域上平均处理的模型参数来描述子系统的状态，故统计能量法结果也是空间和频域平均的结果［14］。统计能量法中，单个子系统i所处的状态用模态密度ni和内损耗因子ηi表示，模态密度是表征子系统吸收和储存能量能力大小的参数，内损耗因子是表征子系统自身对能量衰减强弱的参数。而第i、j 个子系统之间的耦合作用则通过耦合损耗因子ηij表示。多个相互耦合的子系统的功率流平衡方程可表示为

式中：ω 为系统固有频率；Ei为子系统i 储存的能量；Pi为子系统i的外部输入功率；N为子系统个数。

求解式（1）可得到每个子系统的能量，再将子系统的能量按照式（3）转换成相应的动力学指标，即可完成求解。

1.2 SEA子系统的建立

子系统划分需满足模态相似准则，即要求一个子系统所包含的部件必须有相同的动力学特性［14］。在工程应用中，通常结合模型划分子系统，如不同材料、不同厚度的结构划分为不同的子系统；为了保证各声腔子系统的严格封闭性，即使可以划分为同一子系统的结构，也须根据声腔子系统划分为两个或多个子系统［15-16］。

根据子系统划分原则，建立某款紧凑型SUV 统计能量法整车模型，如图1所示，共包含16个声腔子系统和175个结构子系统。声腔子系统如表1所示；而结构子系统则主要包括玻璃子系统、防火墙子系统、地板子系统、顶棚子系统、立柱子系统和车门子系统等。其中，玻璃子系统用平板单元建模，立柱子系统用梁单元建模，其他结构子系统采用曲面板单元建模。

图1 统计能量法模型

表1 声腔子系统

在统计能量法模型中，各子系统之间的耦合方式分为点、线、面3 种形式。线连接是结构子系统之间的主要连接形式，线连接的交点处则为点连接，声腔与声腔、声腔与结构之间则以面连接的形式保证子系统之间的耦合。

1.3 SEA参数计算

统计能量法参数包括模态密度、内损耗因子和耦合损耗因子。采用理论公式［14-15，17］计算各个子系统的模态密度、内损耗因子和各子系统之间的耦合损耗因子。下面分析计算结果。

图2（a）为左前、左后风窗玻璃和驾驶员侧车窗玻璃子系统的模态密度。由图可知，平板子系统模态密度不随频率变化。图2（b）为声腔子系统的模态密度，其随频率增大而增大。

图3（a）和图3（b）分别为玻璃子系统和声腔子系统的内损耗因子。由图可见，玻璃和声腔子系统的内损耗因子随频率升高而减小，相对而言，玻璃子系统的内损耗因子变化较平缓。

图4（a）为左、右防火墙子系统的耦合损耗因子，其随频率升高而减小，在中心频率为630～1 250 Hz的区间减小较快，而中心频率为1 250～6 300 Hz 的区间减小缓慢；图4（b）为驾驶员腿部声腔子系统与左前地板子系统的耦合损耗因子。由图可知，随频率升高而减小，且变化较缓慢。

2 激励载荷提取与模型验证

图2 子系统模态密度

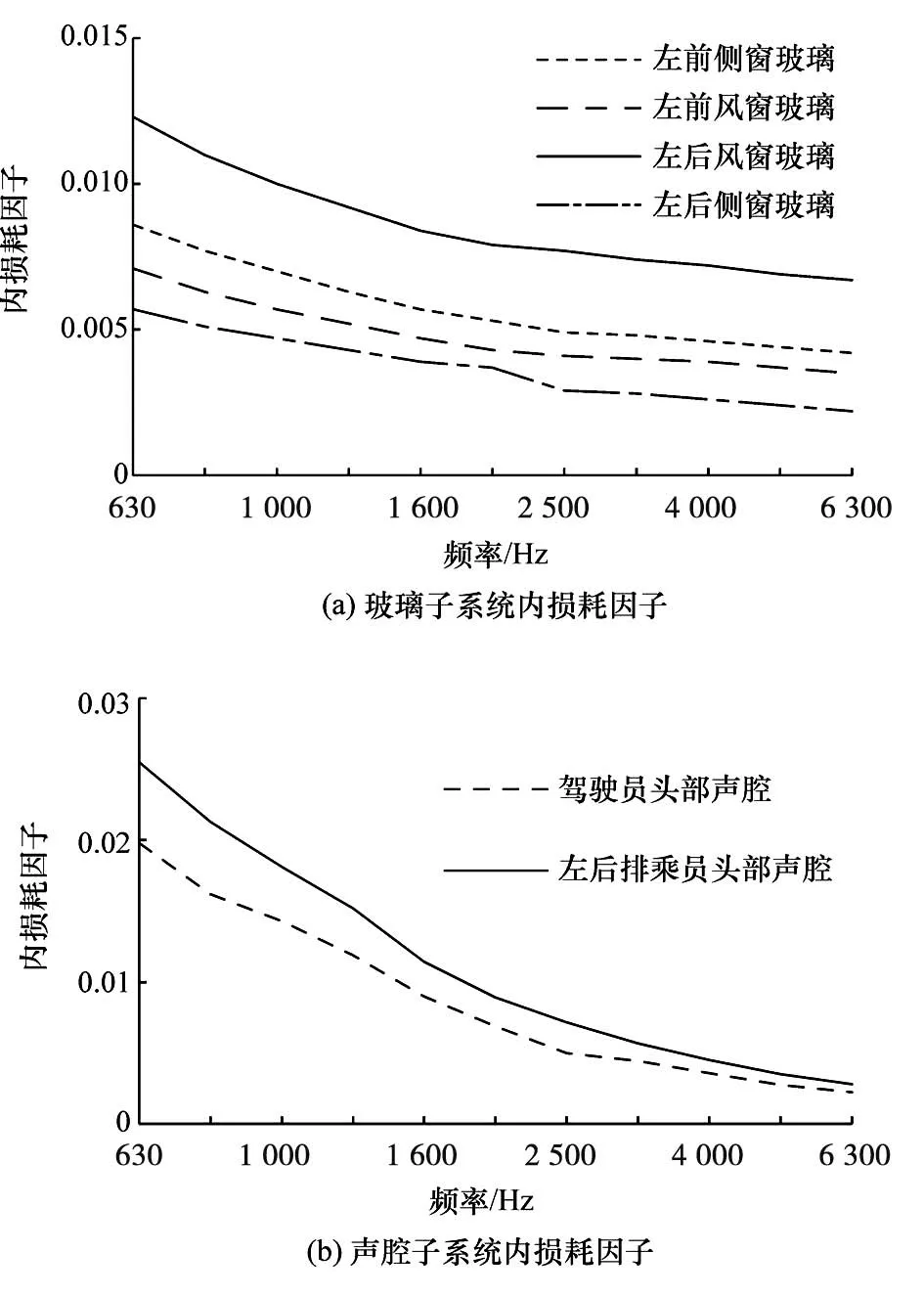
图3 子系统内损耗因子

图4 子系统耦合损耗因子

汽车行驶过程中受到的外部激励可分为结构激励和声激励两种类型。结构激励包括路面不平度激励和动力总成激励等，声激励则包括发动机舱声辐射激励、车身表面脉动压力激励等。在高频分析中，声激励是主要的噪声源，因此分析中主要考虑发动机舱的声辐射激励、车身表面脉动压力激励和动力总成激励。

2.1 发动机舱声辐射激励

发动机舱的声辐射激励测试试验在半消声室进行，车速为80 km/h。在发动机上侧、下侧、左侧、右侧、左防火墙侧和右防火墙侧分别布置3 个传声器，用3 个传声器的平均值代表该表面辐射声压。发动机上侧传声器布置见图5。测试前，先将汽车预热；测试过程中，车身开闭件、车窗玻璃和空调均为关闭状态。最后得到发动机舱声辐射激励1/3倍频程图，如图6所示。

2.2 动力总成激励

通过实车道路测试试验获取动力总成悬置激励，车速为80 km/h。测试过程中分别在动力总成左悬置、右悬置和后悬置被动端安装加速度传感器。图7为右悬置被动端加速度传感器布置图，图8为右悬置测试结果。

图5 发动机上侧传声器布置图

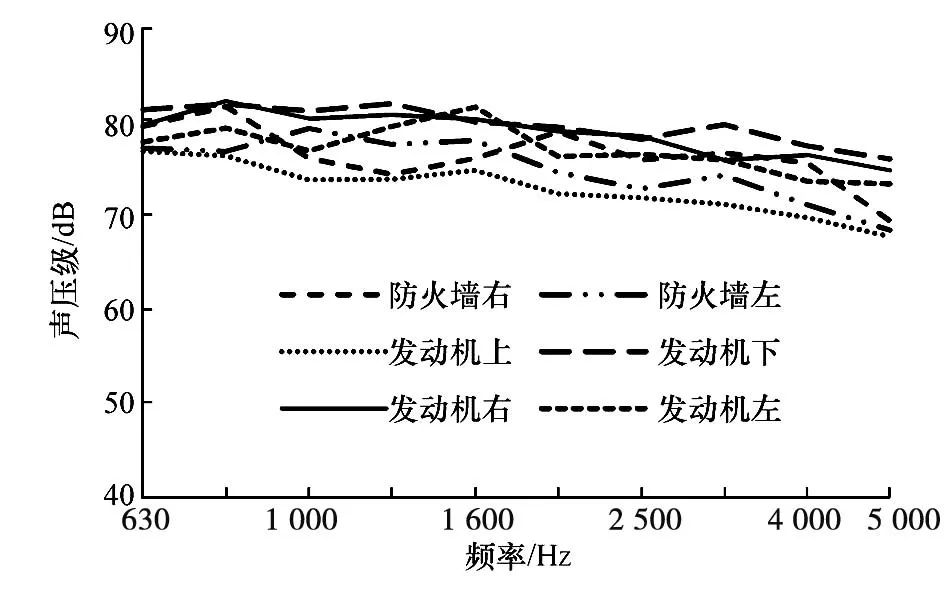
图6 发动机舱声辐射激励

图7 右悬置被动端加速度传感器布置图

图8 右悬置加速度激励

2.3 车身表面脉动压力激励

建立整车计算流体动力学模型，提取车身表面脉动压力激励。计算域尺寸为10L×9W×5H，其中L、W、H 分别表示车长、车宽和车高，计算域如图9 所示。采用Realizable k-ε 湍流模型进行稳态计算，当计算结果收敛后，再以稳态计算结果为初始条件进行瞬态计算提取脉动压力，瞬态计算以大涡模拟为湍流模型，亚格子模型选用WALE。计算边界条件设置如表2 所示。车身表面脉动压力计算结果如图10所示。

图9 计算域划分

图10 车身各表面脉动压力级

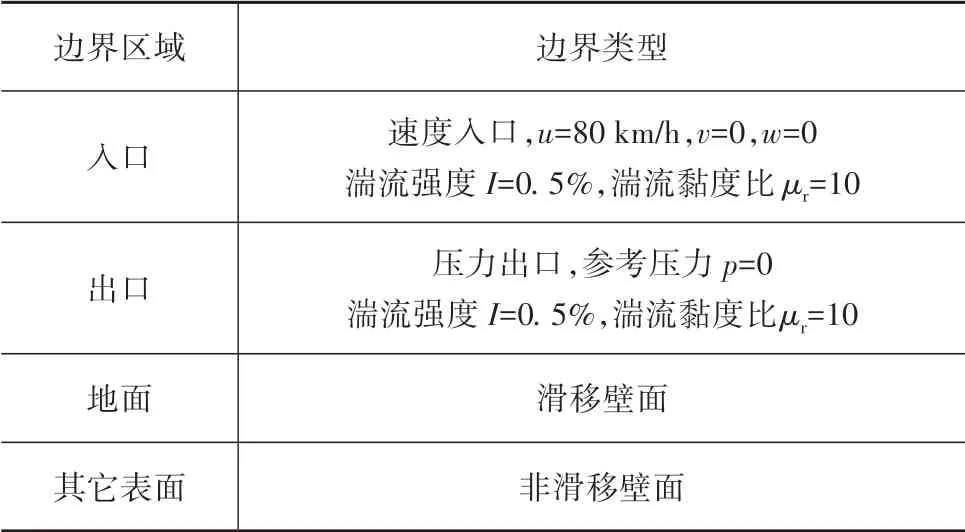
表2 边界条件设置

2.4 模型验证

将试验测试所得动力总成悬置激励施加到前大梁和副车架上，发动机舱的辐射噪声以扩散声场的形式施加到防火墙上，车身表面脉动压力激励以紊流场的形式施加到车身各表面，进行仿真计算，提取驾驶员头部声腔声压，并与实车道路测试获取的驾驶员右耳声压对比，如图11所示。仿真与测试结果吻合较好，说明统计能量法模型具有较高的准确性。

图11 驾驶员头部声腔声压仿真与测试结果对比

2.5 驾驶员头部声腔声压贡献量分析

对驾驶员头部声腔声压进行贡献量分析，结果如图12 所示。由图可知，在630～2 500 Hz 频段，对驾驶员头部声腔声压贡献量较大的子系统主要为驾驶员腿部声腔、前风窗玻璃和左前侧顶棚。当频率高于2 500 Hz 后，前风窗玻璃和侧窗玻璃成为对驾驶员头部声腔贡献量较大的子系统。

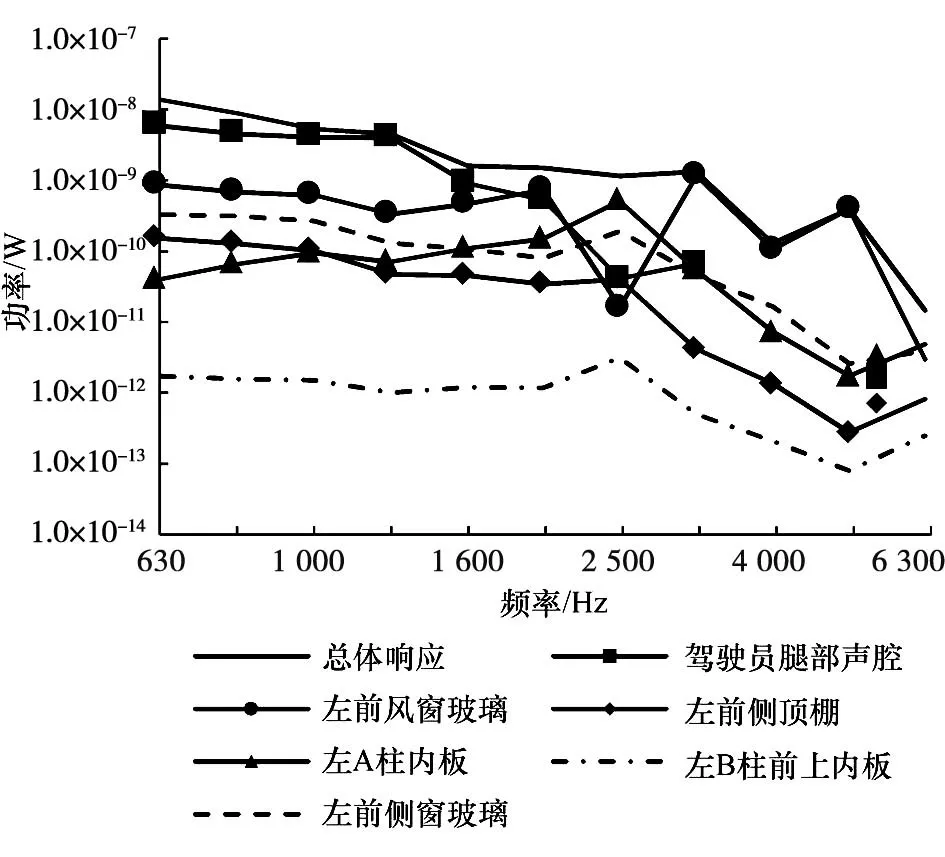
图12 驾驶员头部声腔功率贡献量分析

由于驾驶员腿部声腔是对驾驶员头部声腔声压贡献量较大的子系统之一，且本文不对声腔子系统做改进，故又对驾驶员腿部声腔声压进行了贡献量分析，结果如图13 所示。由图可知，对腿部声腔贡献量较大的子系统主要为防火墙、左前车门前内板、左轮罩板和左前地板等。

图13 驾驶员腿部声腔功率贡献量分析

因此综合结果，对驾驶员头部声腔声压贡献量较大的子系统主要为防火墙、前车门前内板、前风窗玻璃和前地板等。

3 声学包的优化设计

防火墙声学包分为内前围（驾驶室侧）和外前围（发动机舱侧）声学包。下面选择内前围和前地板声学包，从整车声压与轻量化角度对其进行优化。

3.1 声学包改进方案设计

内前围声学包通常为2 层或3 层结构。原车内前围采用EVA+PU 泡沫（80 kg/m3）2 层布置的形式，在原车声学包基础上，将80 kg/m3的PU 泡沫换成31 kg/m3的PU 泡沫，再加1 层毛毡材料，而维持原声学包27 mm总厚度不变，设计改进方案如表3所示。

前地板声学包选择EPDM 为基础材料，以针刺纤维+毛毡组合结构，保持原声学包总厚度22 mm不变，原前地板声学包及其改进方案如表3 所示，各材料参数见表4。

分别计算了改进方案的隔声性能，并与原声学包声学性能对比，结果如图14和图15所示。由图可知，内前围声学包和前地板声学包的改进方案隔声性能优于原车声学包，说明内前围和前地板声学包改进方案设计合理。最后，建立改进方案的优化模型，对声学包各层声学材料厚度做进一步优化。

表3 原车声学包及改进方案

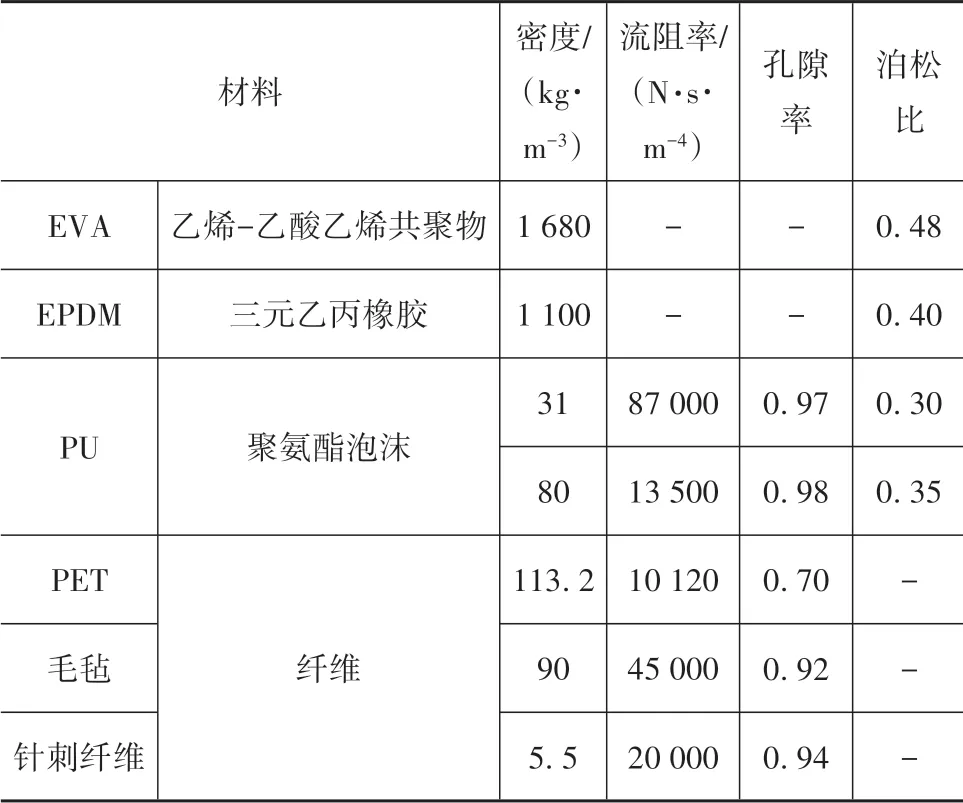
表4 声学包材料

图14 内前围声学包

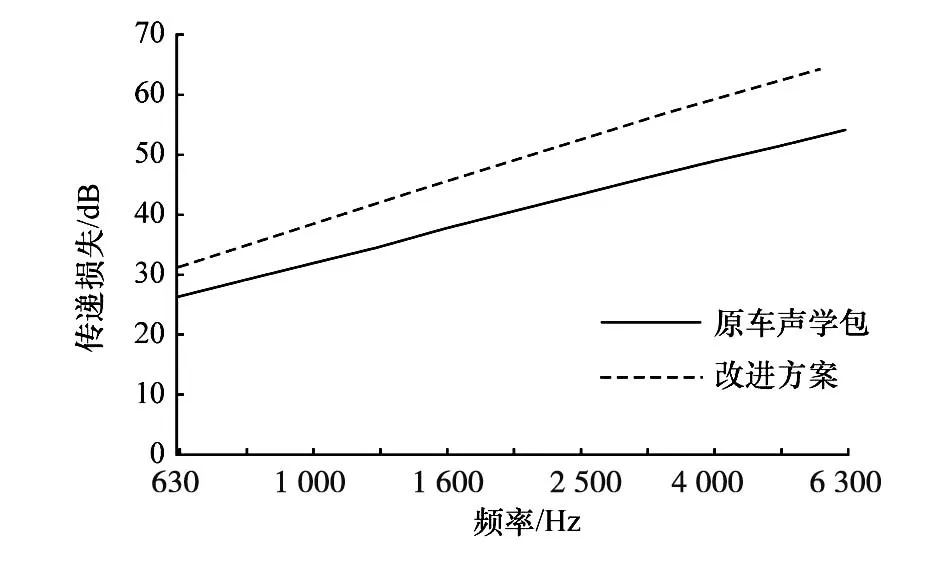
图15 前地板声学包

3.2 声学包改进方案优化

以驾驶员头部声腔总声压级S、声学包总质量M为优化目标，以内前围声学包毛毡厚度N1、PU 泡沫（31 kg/m3）厚度N2和前地板声学包EPDM 厚度D1、针刺纤维厚度D2、毛毡厚度D3为优化变量，以声学材料总厚度作为约束条件建立如下优化模型：

选择拉丁超立方抽样方法抽取60 组样本，并代入模型计算对应样本的目标值，如表5所示。

表5 样本值与响应值

通过样本值与响应值建立三维Kriging 近似模型，选择决定系数R2评价Kriging 近似模型的精度。计算得到声学包总质量的Kriging 模型决定系数为0.88，驾驶员头部声腔总声压级的Kriging 模型决定系数为0.98，均大于0.85，说明近似模型精度满足分析要求。

采用多目标遗传算法对声学包近似模型进行优化。设置遗传代数为50，每代精英数量为样本空间的10%，变异率为0.01。经过计算得到296 组不劣解，构成关于驾驶员头部声腔总声压级和声学包总质量的帕累托前沿，如表6所示。

最后，引入标准边界交叉法在帕累托前沿中寻找最优解［18］。首先对296 组解进行标准化处理，将目标值转为无量纲数；再求解搜索半径R2，获得其最小值为0.81。对应的优化变量结果与近似模型目标值如表7所示。

将优化变量结果圆整后代入原模型中，得到驾驶员头部声腔总声压级为54.03 dB（A），声学包总质量为8.32 kg，声学包优化前后对比见表8。与原方案相比，驾驶员头部声腔总声压级降低0.63 dB（A），声学包总质量降低了2.18 kg，减质量20.76%。

表6 帕累托前沿

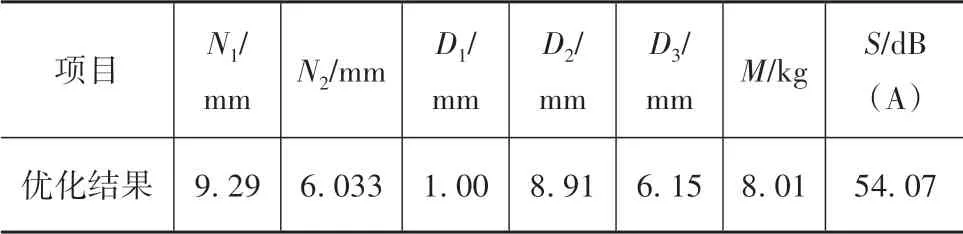
表7 优化结果

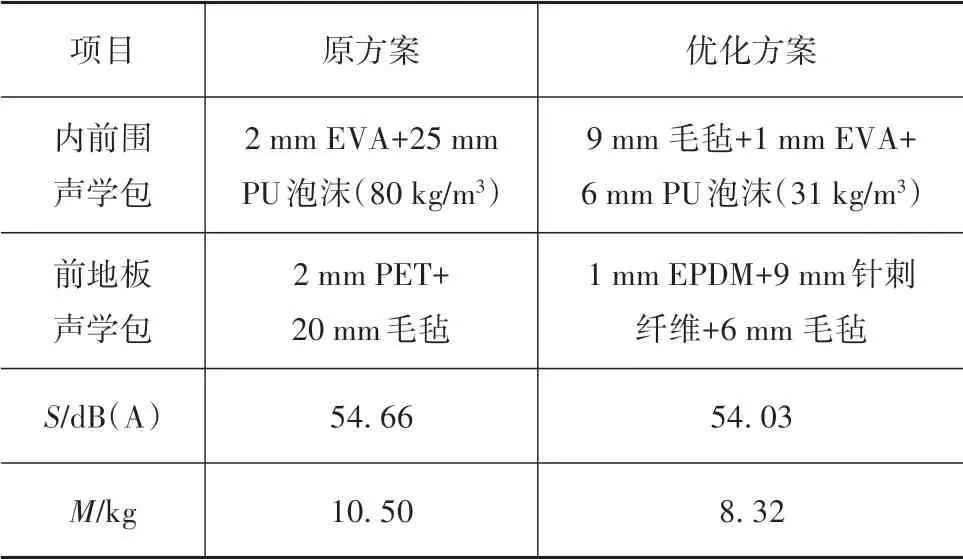
表8 声学包优化前后对比

4 结论

利用统计能量法建立了车内高频噪声分析模型，结合车速80 km/h 匀速工况下的激励数据，预测了驾驶员头部声腔声压，预测结果与试验测试数据吻合较好，说明建立的统计能量法模型可用于高频噪声分析。

在统计能量法模型上，分析了对驾驶员头部声腔声压贡献量较大的子系统，提出了内前围和前地板声学包改进方案，并验证了其可行性。最后，建立了改进方案中各层材料厚度与驾驶员头部声腔总声压级、声学包质量Kriging 近似模型，采用多目标遗传算法对声学包材料厚度进行了优化。优化后两个声学包的总质量减轻了2.18 kg，减质量20.76%；驾驶员头部声腔总声压级降低了0.63 dB（A），既保证了车内的声学性能，也实现了轻量化。