基于试验设计与PSI决策相结合的白车身前端结构轻量化设计*

2021-02-02王登峰李慎华

汽车工程 2021年1期

王登峰，李慎华

（吉林大学，汽车仿真与控制国家重点实验室，长春 130022）

前言

为应对环境保护及能源危机等问题，汽车轻量化引起广泛关注［1-3］。汽车轻量化主要通过轻质材料、先进制造工艺及结构优化设计3 种途径来实现［4］。由于轻质材料和先进制造工艺成本较高难以广泛应用，尤其是经济性车辆，因此结构优化设计技术仍需深入探索。

白车身占整车质量的30%～40%，对其进行结构优化可以显著提高车辆轻量化水平。左文杰等［5］基于刚度、强度及频率约束对白车身薄壁结构进行了尺寸优化。王震虎等［6］基于车身概念模型进行了白车身主断面尺寸优化。王登峰等［7］通过隐式参数化技术优化设计了白车身结构。以上研究均取得了良好的白车身轻量效果，但并未研究白车身结构优化设计后对车辆耐撞安全性能的影响。

Wang 等［8］综合考虑白车身基本静-动态性能及碰撞安全性能，采用RBF 近似模型联合多目标优化算法进行了白车身结构优化设计。张帅等［9］基于Kriging近似模型联合NSGA-II优化算法对白车身前端结构进行了优化设计，实现了良好的轻量化效果。白车身轻量化设计实质是一项涉及白车身弯扭刚度、模态频率和碰撞安全性能的大变量多学科优化设计。针对多学科优化设计问题目前主要是采用近似模型联合优化算法进行迭代优化，但获得理想结果的前提是建立高精度近似模型。白车身碰撞安全性能是一个涉及大变形、高度非线性优化响应。陈媛媛等［10］研究表明，建立一个能够映射车辆碰撞安全性能的高精度近似模型仍是一项挑战。

为避免反复修正近似模型的困扰、提高优化设计效率及丰富白车身结构轻量化设计方法，本文中提出试验设计联合偏好选择指数（preference selection index，PSI）决策的轻量化设计策略。以白车身前端结构为轻量化对象，综合考虑白车身弯扭刚度、一弯一扭模态频率等基本静-动态性能和正撞安全性能约束。通过试验设计获得能够反映整个白车身前端结构轻量化设计空间的备选解，采用PSI法对有限个备选解进行多目标决策，得到最佳轻量化设计方案。

1 白车身性能仿真与试验

1.1 白车身基本静-动态性能

（1）低阶模态频率。白车身1 阶扭转频率fT和1阶弯扭频率fB反映了白车身动态刚度，同时与白车身振动噪声密切相关。采用Lamczos 法提取白车身前6阶自由模态，根据白车身振型确定fT和fB。

（2）扭转刚度ST。ST表征白车身抵抗扭转变形能力。白车身扭转工况设置如图1 所示。在扭转载荷作用下分别测量白车身前端左右减振塔安装孔中心点最大变形量DLmax、DRmax，白车身ST计算公式为

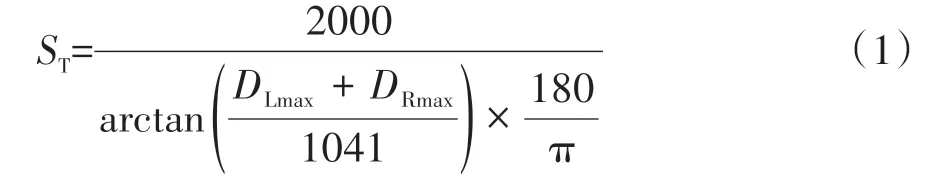
（3）弯曲刚度SB。SB表征白车身在垂直载荷作用下抵抗弯曲变形的能力。白车身弯曲工况设置如图2 所示。分别测量白车身底部左右门槛梁在集中载荷（F=750 N）作用下的最大变形量ZLmax、ZRmax，白车身SB计算公式为

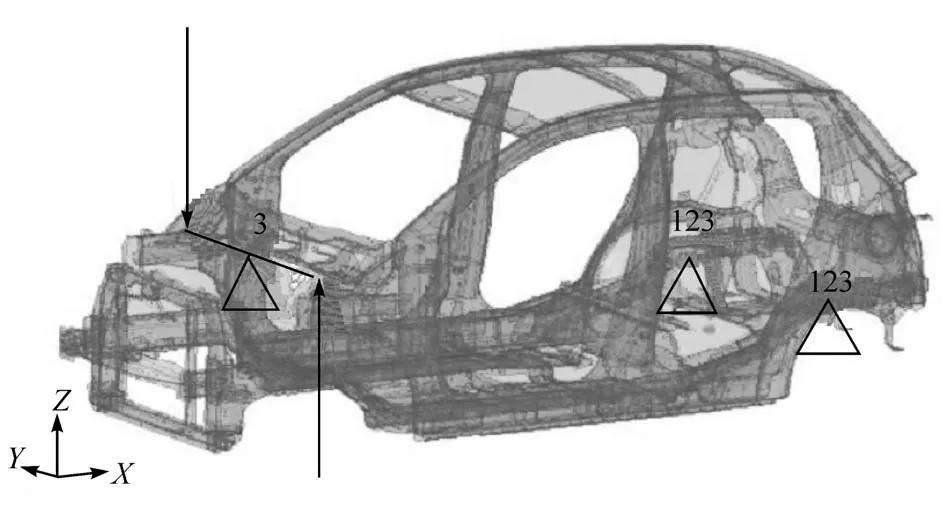
图1 白车身扭转工况

图2 白车身弯曲工况

基于建立的白车身有限元模型，分别对fT、fB、ST和SB进行有限元分析与计算得到白车身基本静-动态性能，如表1所示。

表1 白车身基本静-动态性能

1.2 白车身正撞安全性能

建立整车有限元模型，并按照中国新车评价程序（C-NCAP）2015 版试验规范，设置车辆100%刚性墙正面碰撞仿真分析工况。车辆以50 km/h 的速度垂直撞击刚性墙，车辆前端结构与刚性墙的摩擦因数为0.7。车辆正撞有限元模型见图3。

为评价白车身正撞安全性能，设置白车身正撞安全性能指标为：防火墙最大侵入量DFmax；前门框最大变形量，即A 柱D 点相对于B 柱水平方向最大变形量DDmax；B 柱与门槛梁交叉处“T”点X 向最大加速度ACC。白车身正撞安全性能监控点如图4所示。使用LS_Dyna 软件对车辆正撞有限元模型进行仿真分析，提取白车身正撞安全性指标，如表2所示。

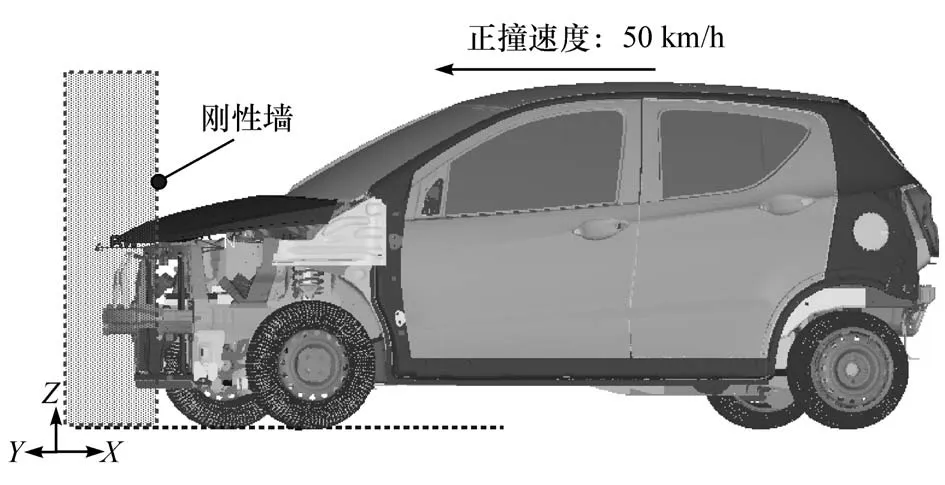
图3 车辆100%刚性墙正撞有限元模型

图4 白车身正撞安全性能监控点

表2 白车身正撞安全性能

1.3 100%刚性墙正面碰撞试验

根据C-NCAP 2015 版100%刚性墙正面碰撞试验规范，对车辆进行正撞试验。试验工况与仿真分析工况一致。B 柱与门槛梁交叉处结构强度高，不易发生破坏，在此位置布置传感器，获取碰撞过程的加速度，并对采集的加速度进行低通滤波。加速度可以反映乘员在碰撞过程所承受的冲击力，是碰撞安全性能最重要的指标。车辆正撞试验如图5 所示。为检验所建立的有限元模型精度，将加速度试验结果与仿真值进行对比，如图6 所示。结果表明，在0-100 ms 时间历程内仿真分析值与试验值除在一些局部小区域有偏差外，整体变化趋势一致。表明本研究所建立的有限元模型具备足够精度。

图5 车辆100%刚性墙正面碰撞试验

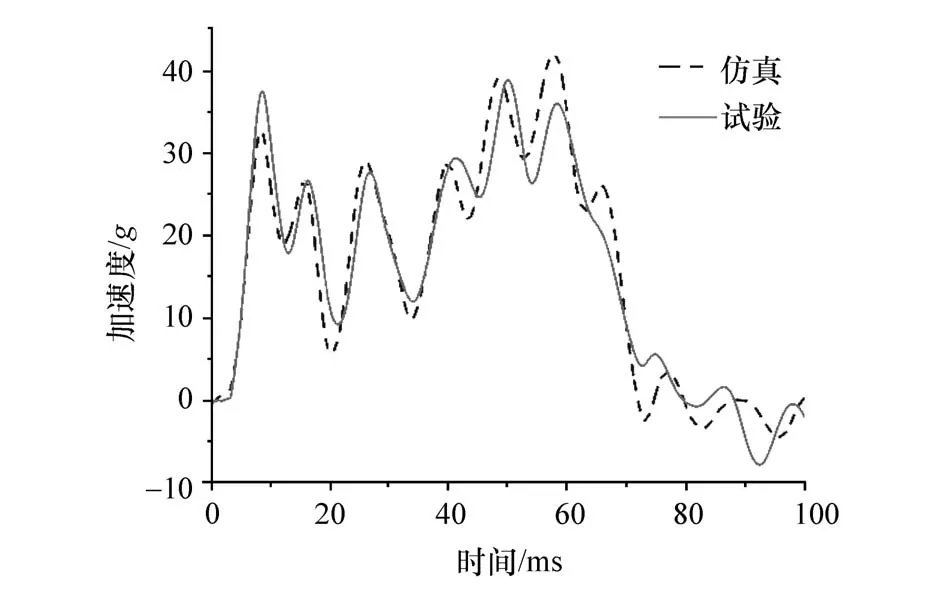
图6 加速度试验值与仿真值比较

根据C-NCAP 2015 版标准，该小型乘用车碰撞试验获得了“五星”安全等级。正撞试验结果表明，该车具备足够的正撞安全裕度，同时存在一定的轻量化空间。为充分发挥材料利用率避免冗余设计，结合企业经验及碰撞安全等级“五星”阈值，制定该白车身前端结构轻量化设计的基本静-动态性能基线如表3所示，正撞安全性能基线如表4所示。

表3 白车身基本静-动态性能基线

表4 白车身正撞安全性能基线

2 白车身前端结构设计变量筛选

2.1 白车身前端结构初始设计变量

根据车辆正撞工况下力的传递路径及零部件吸能量，将白车身前端26 组零件（包含对称件）的壁厚作为轻量化初始设计变量，如图7所示。

2.2 初始设计变量的贡献度分析

26 组初始设计变量对白车身前端结构质量M、白车身基本静-动态性能及碰撞安全性能响应的影响程度不同。为提高优化设计效率，缩减样本空间，对初始设计变量进行贡献度分析获得最终设计变量。

系统的性能响应可以通过设计变量的回归模型进行近似表示：

图7 白车身前端结构初始设计变量

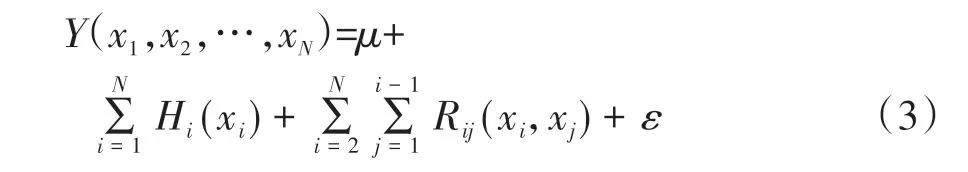
式中：Y 表示系统性能响应；xi表示设计变量；表示设计变量的主效应表示任意两个设计变量的交叉效应；μ 为常数；ε 为误差值；N为变量个数。

设计变量主效应可以近似表示为式（4）。因此，设计变量对响应的贡献度定义为

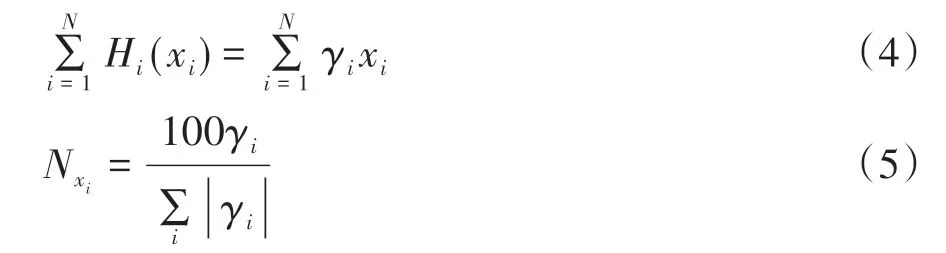
式中：γi表示通过最小二乘法得到的设计变量主效应系数；Nxi表示设计变量对响应的贡献度。

基于以上贡献度分析原理，分别计算得到26 组初始设计变量对白车身质量、基本静-动态性能及碰撞安全性能的贡献度结果，如图8 所示（由于篇幅限制仅列出设计变量对部分性能响应的贡献度结果），正值表示正相关贡献度，负值表示负相关贡献度。

通过分析26 组初始设计变量的贡献度结果，筛选出对白车身质量、基本静-动态性能及碰撞安全性综合影响较大的20 组变量作为最终设计变量，如图9所示。

3 白车身轻量化结果

3.1 白车身轻量化试验设计

（1）试验因子。将通过贡献度分析筛选出的20组壁厚设计变量作为试验因子，因子的变化范围为每个壁厚初值的70%～110%。

图8 设计变量的贡献度结果

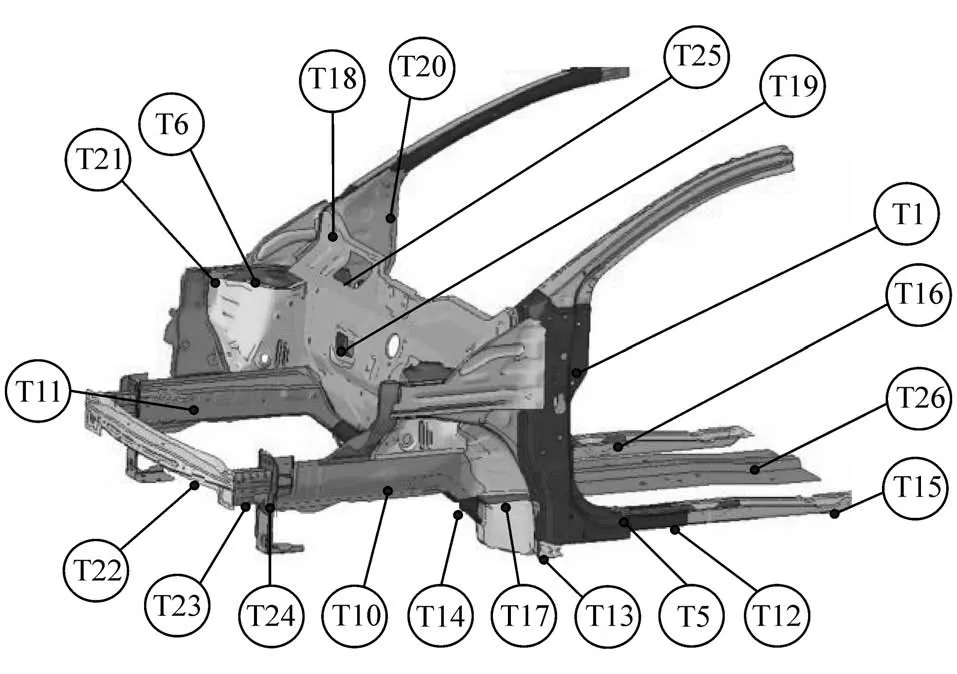
图9 白车身前端结构最终设计变量

（2）试验设计矩阵。Hammersley 采样是在拉丁超立方采样的基础上改进而来，既有单一维度的均衡性又有良好的空间填充性，可用较少的样本点来反映整个设计空间。为充分填充整个轻量化设计空间，给设计人员提供更多的轻量化备选方案以达到较好的轻量化效果，对20 个试验因子基于Hammersley 采样法生成120 组样本点构造试验设计矩阵，如表5所示。

（3）试验设计结果。将试验设计矩阵中的120组样本点分别赋予已建立的有限元模型进行仿真分析和计算。使用8 核3.60 GHz 的计算机，每一个样本点计算（车身基本静-动态性能及整车碰撞）大约11 h，得到相应的120 组试验设计结果，如表6所示。

根据试验设计结果可知，白车身前端结构质量、基本静-动态性能及正撞安全性能指标间有的相互矛盾冲突、整体趋势也变化不一，难以直接选出一组最优解。因此，须进行多目标决策。

表5 试验设计矩阵 mm

表6 试验设计结果

3.2 白车身轻量化试验设计结果PSI决策

PSI 是一种多目标决策方法。当多个目标之间相互矛盾难以决策时，PSI 根据统计学原理计算多个目标的总体偏好选择指数Pi，依据Pi大小对备选方案进行排序获得最佳理想方案。现有的其它多目标决策方法需要对每个目标进行权重分配，不同的权重分配直接影响最终的决策结果，且合理的权重确立需要复杂的计算。然而，PSI 法在多目标决策时无须赋予目标之间的相对权重，这是该方法的优点。因此，本文中提出采用PSI 法对白车身轻量化试验设计结果进行决策分析，获得最佳轻量化设计方案。

基于PSI 法的白车身轻量化设计方案决策流程如下。

（1）定义决策矩阵

式中xij表示第i个试验设计结果的第j个目标值。

（2）数据归一化处理

白车身前端结构质量、模态频率、弯扭刚度和正撞安全性能的单位不同，在决策过程中具有不可公度性。须通过归一化处理将不同单位、不同大小的属性数据转化为［0-1］范围的无量纲规范化数据。不同特性的目标数据归一化方式不同，fT、fB、ST和ST具有望大特性（收益性指标），归一化处理公式为

M、DFmax、DDmax和ACC具有望小特性（成本性指标），归一化处理公式为

式中：rij为xij的归一化结果表示第j 个性能指标的最小值。

（3）计算偏好变化值PVj

利用样本方差类比的概念，使用以下公式确定每个目标的偏好变化值PVj：

（4）计算总体偏好值αj

计算总体偏好值须获得PVj的偏差βj：

总体偏好值的计算如下：

（5）获得偏好选择指数Pi

Pi数值越大表示备选方案的轻量化综合效果越好。

根据以上PSI计算流程，对表6中白车身轻量化试验设计结果进行计算，得到决策结果如表7 所示。图10 示出所有试验设计方案的Pi值信息。根据Pi值大小排序结果可知，第95 组轻量化方案的Pi数值最大排序第一。因此，将白车身轻量化试验设计的第95 组试验因子作为白车身前端结构的最佳轻量化方案。

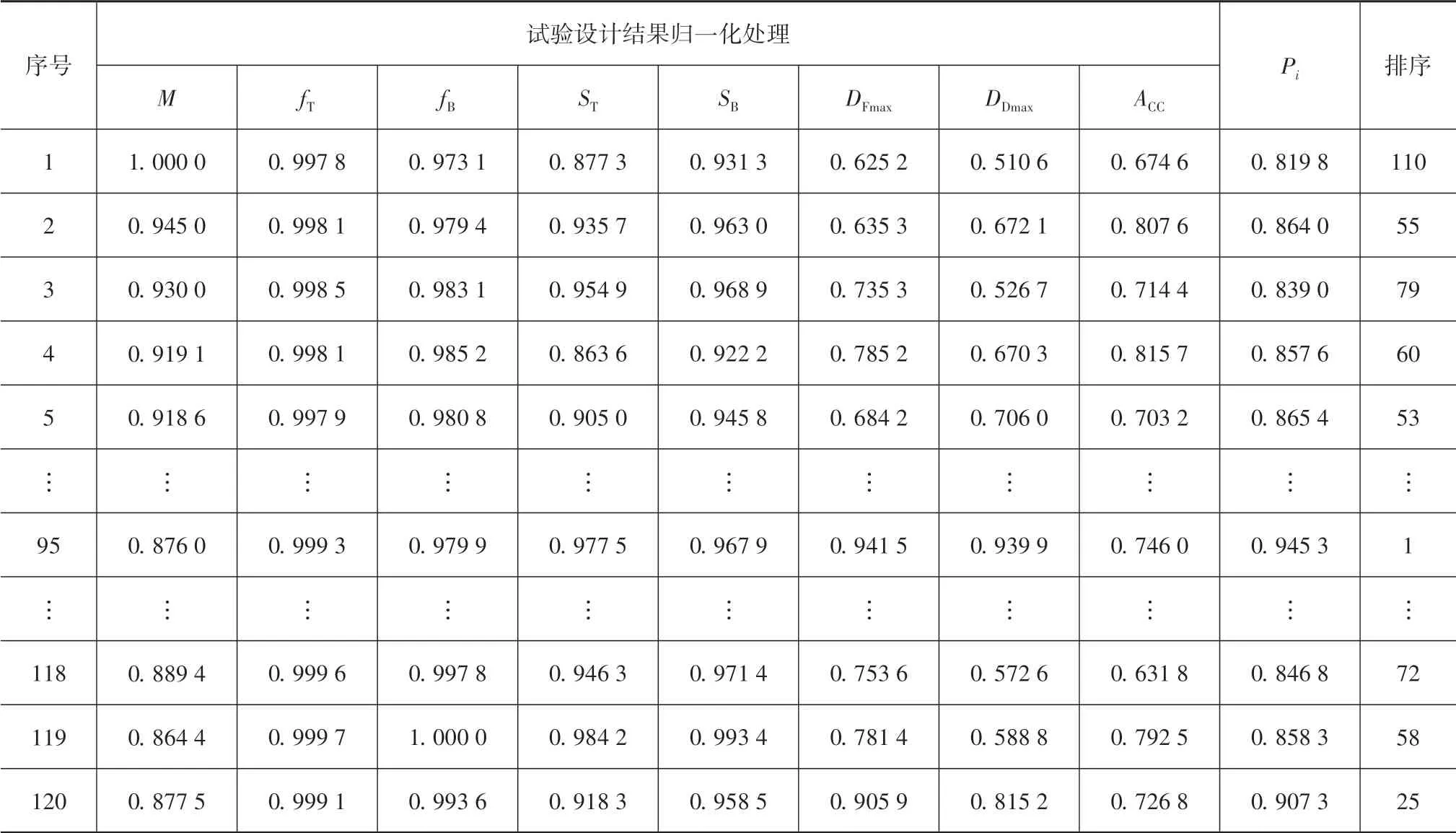
表7 PSI决策结果

图10 试验设计方案的偏好选择指数Pi

3.3 白车身轻量化结果对比

根据汽车钢板的常用厚度规格，以0.05 mm 的变化梯度对表5中的第95组试验因子进行参数圆整以满足实际应用。圆整后的因子参数重新赋予到有限元模型进行仿真分析，计算得到最终白车身前端结构质量、基本静-动态性能及正撞安全性能参数值，如表8中“轻量化后”栏所示，相比于初始值变化如“改变”栏所示。白车身前端结构轻量化设计后质量减轻4.43 kg，轻量化率达7.23%，白车身基本静-动态性能及正撞安全性能有增有减但均满足设计基线要求。轻量化后车辆前端变形模式如图11 所示。轻量化后的正撞安全性能与初始性能详细对比如图12所示。

3.4 方法比较

图11 车辆前端变形模式

响应面等代理模型结合优化算法是一种常用的车身结构轻量化优化设计方法。根据响应面算法对样本点数量要求及陈媛媛等［10］研究表明，构建一个涉及整车耐撞性的高精度代理模型至少需要（N+1）×（N+2）/2 个样本点且需要修正，N 为设计变量个数。针对本文的20 个设计变量采用响应面代理模型至少需要231 个样本点，计算总时长为2 541 h。大量文献［11-14］研究表明，采用代理模型及优化算法进行车身结构优化，轻量化率一般低于10%，否则将以牺牲车身性能为代价。本文中试验设计联合PSI决策方法计算总时长1 320 h，相比于代理模型结合优化算法的优化效率提高了48%。在满足车身性能设计基线要求的前提下，轻量化率达到7.23%，取得了较好的轻量化效果。因此，试验设计联合PSI 决策相比于代理模型结合优化算法更好地权衡了优化效率和轻量化效果之间的关系。尤其在研发周期紧、计算资源有限的情况下，该方法为车身轻量化设计提供了一条新的途径。